泄洪洞补气洞面积设计合理性评估方法研究

张 鹏 飞,宋 凯,徐 鹏

(1.黄河水利职业技术学院,河南 开封 475000; 2.长江勘测规划设计研究有限责任公司,湖北 武汉 430010;3.国家大坝安全工程技术研究中心,湖北 武汉 430010)

0 引 言

泄洪洞在运行时,往往需要通过补气洞向洞内补充空气[1],如果补气洞设计较小导致补气量不足,泄洪洞内将产生较大的负压,降低掺气设施的掺气效果,增加空蚀破坏的风险[2]。因此,如何向泄洪洞内提供足够的空气就显得极为重要。

针对泄洪洞通气问题,国内外学者开展了大量研究[3-5],重心主要围绕在通风量的计算。如岳书波等[6]通过模型试验测量结果发现,泄洪洞补气量并不会随着水流流量的变化而变化,其进气量大小只与闸门后的水流弗劳德数相关;刘昉等[7]以锦屏一级水电站原型观测试验为基础,认为补气洞进气量随流量增大而增大,洞顶余幅会影响进气量,洞顶余幅越小,进气量相应减小;Yazdi等[8]利用Fluent计算软件模拟了泄流底孔的水流运动过程,并将模拟得到的洞内空气流场数据与模型试验实测值对比分析,证明了VOF方法结合标准k-ε紊流模型可以用来计算补气洞的需气量;李美玲等[9]运用数值模拟方法,认为通风面积增大会导致补气量增多,但增大到某一定值后便不再增加;Wei等[10]通过数值计算拟合得到了预测通风量的公式。另一部分学者[11]从理论分析的角度来计算通风量,对预测通风量亦具有重要的指导意义。

如何建立补气量和风速之间的平衡,仍是行业上亟待解决的问题。SL 279-2016《水工隧洞设计规范》[12]规定:“掺气设施应包括与外界连接送气的通气孔,通气孔工作时,孔内最大风速最好不超过40～60 m/s”。而在实际工程中,往往由于补气洞设计的不合理,导致在运行过程中出现极大的风速和噪音。邓军等[13]在对锦屏一级泄洪洞进行原型观测时发现,通风井内风速最大可达120 m/s,远远超出规范限定的最大风速范围,这对建筑物的安全以及工作人员的健康造成极大伤害。并且在后续的研究中发现其补气量偏小,在运行时存在空化空蚀的风险[14]。

目前针对补气洞风速的研究较少。王孝群[15]针对锦屏一级泄洪洞补气洞风速超过规范中限值的问题,提出了多洞供气系统优化设计的方法。Lian等[16]研究了泄洪洞通气流场特性,并对补气洞截面尺寸进行了优化,但只是针对锦屏一级工程,因此在应用上具有较大的局限性。蒋峰等[17]通过数值模拟,对明流泄洪隧洞中通风补气设施局部体型条件下噪声强度进行系统研究,分析了通风噪声产生的主要原因,研究了不同风速及典型局部体型对通风噪声的影响规律,提出了“保证通风量、降低风速、降低噪声”的通风补气降噪优化设计原则。

本文在前人研究的基础上,采用数值模拟的方法研究补气洞面积对其补气特性的影响规律,提出预测补气洞风速的计算公式,并结合规范对风速的要求,提出一种评估补气洞面积大小合理性的方法。

1 研究方法

本文通过Fluent来模拟水气二相流运动[18-19]。计算的体型较为规整,所以计算区域大部分采用的是结构化网格。本文数值模型选取RNGk-ε双方程湍流模型,是模拟高速湍流流动[20]的有效方法。采用VOF法处理自由水面。连续方程、动量方程、k方程、ε方程如下:

(1)

(2)

(3)

(4)

式中:t为时间;ui和xi分别为速度分量和坐标分量;σk,σε分别为紊动能和耗散率所对应的Prandtl数;Gk为紊动能k的产生项;ρ为流体密度;k为紊动能;ε为紊动能耗散率,其余项可参见文献[20]。

VOF模型已经被证实非常适用于自由表面流以及液体不混合分层流[21],所以本文采用VOF模型追踪固定欧拉网格上的水气界面。VOF方法认为任意一个计算区域单元都是由水和气这两相组成,并且水和气的体积分数之和为1。定义αw为水的体积分数,规定:αw=0表示控制体内全为空气;αw=1表示控制体内全为水;0<αw<1表示控制体内为水气混合物。水气界面通过求解下面的连续方程跟踪:

(5)

本次研究以RM水电站放空洞为依托,放空洞布置如图1(a)所示,有压洞段长度为369.5 m,底板坡度i=0,洞身断面型式为城门洞型,断面尺寸为7.0 m×15.5 m;无压洞段长度为975 m,底板坡度i=4.73%,洞身断面形式亦为城门洞型,断面尺寸为11.0 m×15.0 m。有压洞段与无压洞段由弧形闸室连接,弧形闸门孔口尺寸为7.0 m×13.0 m,补气洞布置于弧门闸室上方,横截面为矩形,与闸室等宽,见图1(b)。

图1 数值计算模型示意Fig.1 Schematic diagram of numerical calculation model

设置计算域时,定义底板和边墙以及顶板均为固定边界(wall),对于近壁面流动,采用标准壁面函数法来计算。空气进口采用压力进口边界(pressure inlet),压力为当地大气压;出口边界采用自由出流,设定为压力出口边界(pressure outlet),压力为当地大气压,空气、水均可自由进出。

使用gambit网格划分工具进行建模和划分网格,网格的密度在很大程度上影响数值计算结果的可信度,通常网格尺寸越小,计算结果就越可靠,但同时网格数量的增加会大大降低计算的效率。为此,首先进行网格无关性检验,其具体方法是:对模型划分一系列数量、密度不同的网格并依次迭代计算,若前后两次数值解偏差小于1.5%,即可通过网格无关性检验。分别控制最小网格尺寸为0.2,0.5,1 m以及2 m的数学模型进行运算,发现当网格尺寸小于0.5 m后,计算结果差异很小,考虑到计算速度和精度要求,选择网格最小尺寸为0.5 m进行数值模拟,总网格数量约为200万个。

2 模型验证

由于空气流速的测量结果受到模型缩尺效应的影响极大,本文利用比尺为1∶15的物理模型试验结果进行验证,模型为正态水工模型(见图2),遵循重力相似准则。在原型运行水头66.0 m工况下,模型水头为4.4 m,模型流速超过8.3 m/s,大于临界速度,能真实反映流速分布特点。为保证流速测量的准确性,采用毕托管测量水流流速。将模型试验测量的无压隧洞沿程流速换算为原型值,变化范围为23.06～33.58 m/s;数值计算无压隧洞沿程流速变化范围为24.50～37.93 m/s,相对平均误差值为6.0%。取下游稳定段某断面,测量其水流流速及断面风速并换算为原型值,测量结果如图3所示。

图2 1∶15物理模型布置Fig 2 Layout of physical model with scale of 1∶15

图3 模型验证Fig 3 Model verification

进行流量验证时,考虑到1∶15比尺模型的供水能力,试验工况最高水位为76.0 m,数值模拟计算结果与模型试验结果之间的相对误差均小于5%,证明计算模型可靠。

3 工况设计

拟定6种运行水头h0,分别为150.0,130.0,110.0,90.0,76.0,66.0 m,通过计算得到各运行水头下的水力参数见表1。本文主要研究补气洞截面积A(长a×宽b)对补气特性的影响规律,因此共设置11种不同的补气洞截面积,分别为7.0 m×(3.0～18.2 m)。在分析时引入面积系数β的概念,即补气洞截面积A与洞顶余幅面积A0的比值。不同水位时放空洞内的平均洞顶余幅ε不同,因此β也会随之变化,具体数值见表2。

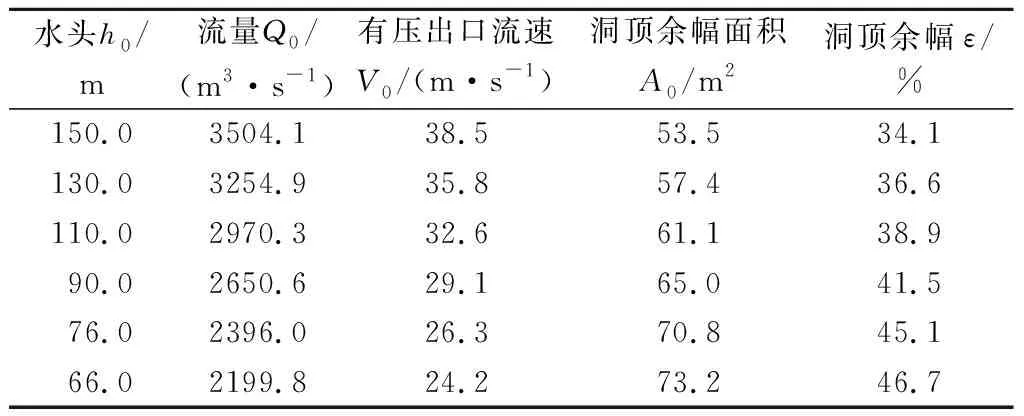
表1 水力参数值Tab.1 Hydraulic parameter values

表2 面积系数值β(补气洞面积A/洞顶余幅面积A0)Tab.2 Area coefficient values β(ratio of air supply tunnel area A to residual roof area A0)

弧门闸室上方的补气洞是放空洞唯一的通风设施,可以视为一个相对封闭的通气系统;且无压段长度与洞高之比大于38,可保证此系统内全部的空气量都由补气洞进入,对计算结果分析时未发现逆向补气现象。

4 补气洞内风速预测公式

以最高水头工况(即有压段出口流速V0=38.5 m/s)为例,分析几种典型补气洞面积下的计算结果。图4为β取不同值时洞内空气流场分布。从流场图可以明显地看出,洞内风速随着β值的增大而减小。将风速大小进行量化处理,图5显示了补气洞截面积与洞内空气流速大小的曲线关系。当补气洞面积为初始设计尺寸(7.0 m×3.0 m)时,补气洞内的平均风速超过80 m/s,约为水流流速的2.1倍,远高于规范规定的最高风速范围(40～60 m/s),在高速水流条件下不仅会造成极大的噪声污染,甚至可能引发结构振动。随着补气洞面积增大,平均风速明显减小,表明在补气洞面积较小时,风速受面积的影响较大,但随着补气洞面积的增大,其对风速的影响逐渐变小,补气洞风速并不是随着补气面积的增大而无限减小。所以,适当增大补气洞面积能有效减弱高风速带来的噪音与振动,保障结构安全。

图4 补气洞内空气流速分布(V0=38.5 m/s)Fig.4 Distribution of air velocity in the air filling cave (V0=38.5 m/s)

图5 补气洞进口风速与面积系数β的关系曲线(V0=38.5 m/s)Fig.5 Relationship curve between wind speed in the air-filling cave and area coefficient β(V0=38.5 m/s)

分析不同水流条件下补气洞面积对风速的影响,对补气洞内风速进行无量纲化处理,结果见图6,空气流动速度用V表示,水流速度用V0表示。从图6中可以看出,在各水流速度下,补气洞内的风速随面积系数的变化规律基本相似,即随着面积系数的增大,补气洞内风速呈逐渐减小的趋势,且最终趋于某固定值。拟合数值模拟计算结果,可以得到补气洞内平均风速与面积系数以及水流速度关系式:

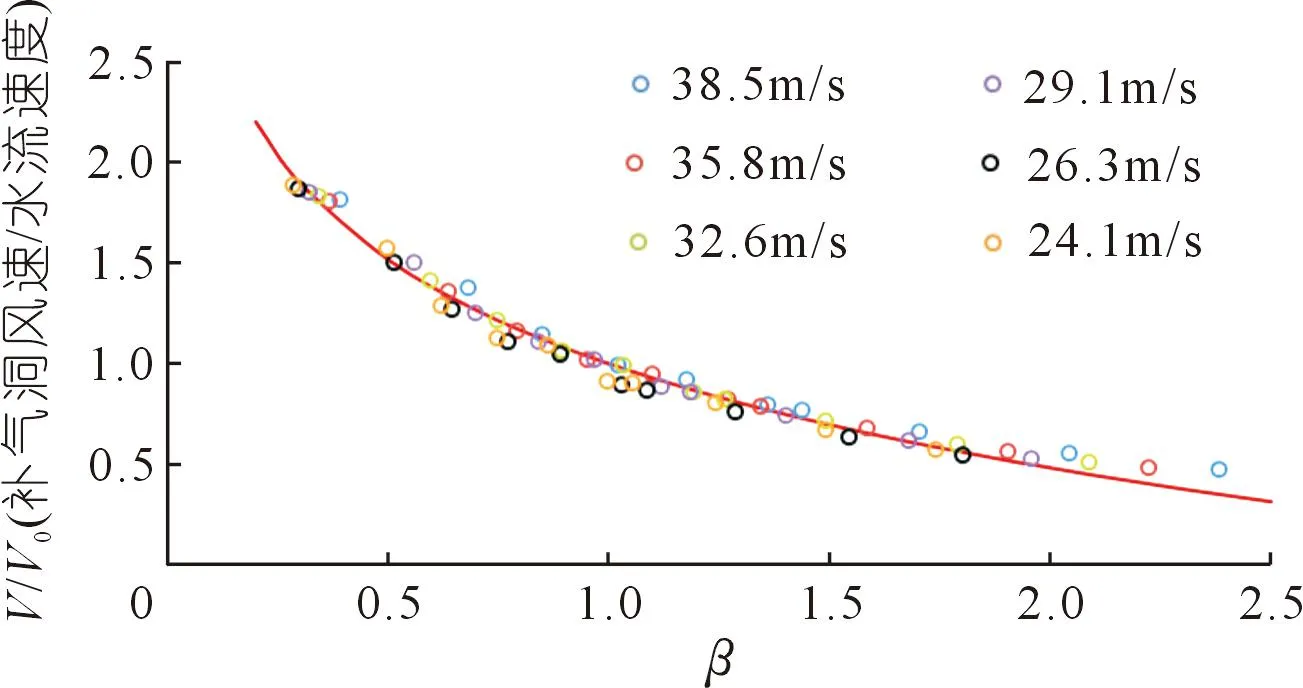
图6 补气洞进口风速与水流速度以及面积系数的关系曲线Fig.6 Relationship curve between wind speed, water velocity and area coefficient β in the air-filling cave

(6)

结合锦屏一级水电站泄洪洞补气系统来验证该公式。锦屏一级水电站泄洪洞共设置了3条补气洞,补气系统如图7所示。其中1号洞与2号洞之间距离较长,可以认为互相不受影响,3号洞位于最末端且距离2号洞较近,会受到上游补气洞的影响,因此以1号和2号洞作为验证对象。采用公式(6)计算时,以各洞段之间的平均水流速度和洞顶余幅作为计算标量。原型观测数据与公式预测值对比结果见表3。预测值与观测结果误差均小于10%,可以认为预测公式(6)是可靠的。

表3 风速原型观测数据与公式计算值对比Tab.3 Comparison of wind speed prototype observations values and formula calculations results

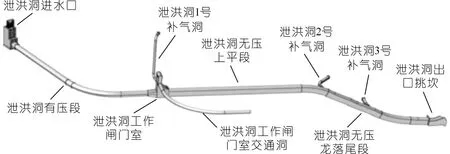
图7 锦屏一级水电站泄洪洞补气系统布置示意Fig.7 Schematic diagram of air-filling system arrangement of the flood relief cave in Jinping Ⅰ Hydropower Station

5 补气洞设计合理性评估

5.1 评估方法

结合SL 279-2016《水工隧洞设计规范》进一步分析补气洞内风速场,其有明确的规定:通气孔在正常工作时,孔内风速最大值不超过40～60 m/s。不同水流条件下的面积系数β与补气洞风速之间的关系曲线如图8所示,在之前的研究[22]中笔者提出,当β≈1时,补气洞的补气能力值λ达到最大,以λ≥0.9作为设计参考值,对应的β值范围为0.8≤β≤1.1。

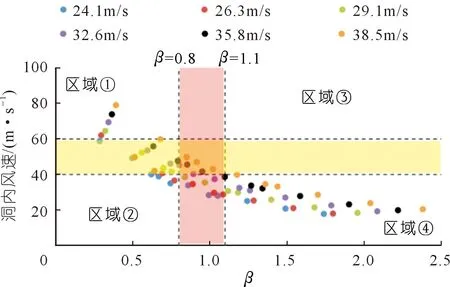
图8 不同水流速度条件下β与补气洞内风速的关系Fig.8 Relationship between the area coefficient β and the wind speed in the air-filling cave under different water velocity conditions

根据补气洞的补气能力及洞内风速对设计方案进行评估,对图8进行区域划分。图中黄色区域和粉色区域为过渡带,黄色区域内风速为规范临界值,粉色区域内补气能力为设计参考值,这两个区域作为评估的分割线。区域①的特点是高风速但补气能力弱,风速超过规范允许范围的同时补气能力无法满足运行所需;区域②的特点是低风速且补气能力弱,虽然风速值在允许范围之内,但是补气量无法满足要求,只能通过增设补气洞的方式增大供气量;区域③的特点是高风速且补气能力强,虽然补气能力达到要求但是过大的风速对结构安全和环境健康造成极大威胁,并且补气洞的面积偏大不利于投资,在设计时应当避免出现;区域④的特点是低风速但补气能力强,是通过增大补气洞面积的方式来减小洞内风速,对于设计来说缺乏经济性。

从图8中我们还能发现,β～V曲线基本上分布于区域①、②和④这3个区域,对于区域③,想要同时满足补气能力和风速超过最大允许值两个条件,只有水流在超高流速的情况下才能达到,在目前的水利工程泄洪隧洞中几乎没有出现。对于区域①,在水流条件不变的情况下,可以通过增大β值即增大补气洞面积的方法使设计值向合理区移动;对于区域②以及区域④,应当尽可能调整设计参数β值,越靠近粉色区域,越经济合理。

5.2 工程实例

在已知水力参数(水流速度及洞顶余幅)的前提下,可以通过公式(6)得到补气洞(设计为不同面积时)内近似风速,不仅能够预测补气量,还能判断风速是否在规范范围之内,进而评估设计的合理性,并对设计体型提出改进方案。

5.2.1锦屏一级水电站补气洞

图9中两条曲线分别代表了1号补气洞和2号补气洞用公式计算得到的洞内风速与面积关系。可见观测值与计算值之间的差异,并以此推断出设计的合理性。

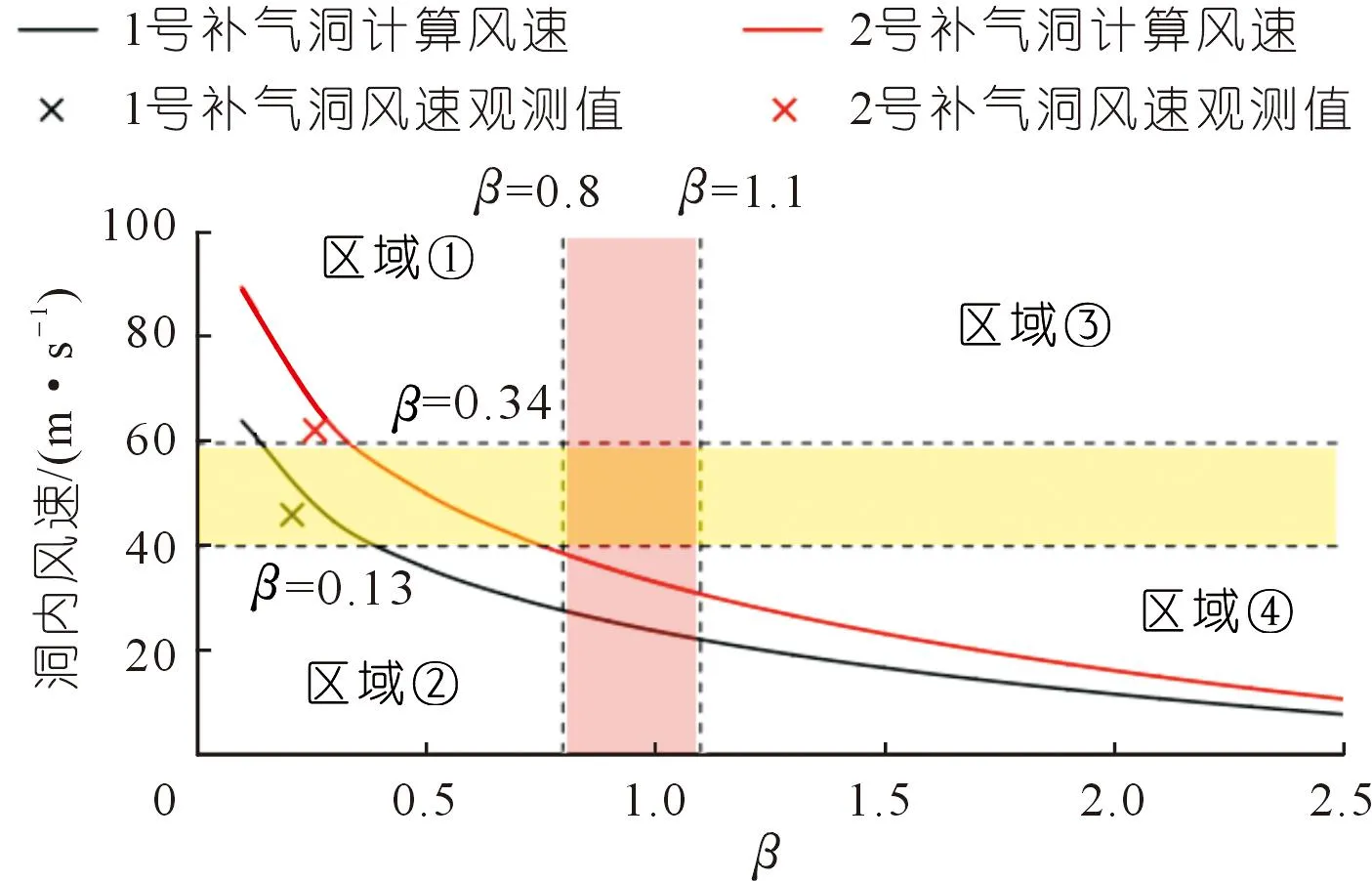
图9 锦屏一级水电站补气洞设计合理性评估Fig.9 Design evaluation on performance of air-filling cave in Jinping I Hydropower Station

对于1号补气洞,洞内风速值4060 m/s,处于区域①,表明2号补气洞设计的面积偏小,若使风速满足规范要求,应增大补气洞面积,使得β2≥0.34,对应的补气洞面积为47.1 m2,即2号补气洞面积应大于47.1 m2。具体设计方案还应当考虑工程的实际情况。

5.2.2RM水电站补气洞

RM水电站放空洞有压出口处设有一条补气洞(见图1)。补气洞截面积为35 m2,在设计水位下运行时,水流速度为24.2 m/s,面积系数β=0.65,根据公式(6)计算得到补气洞内风速为32.0 m/s;在最高水位下运行时,水流速度为38.5 m/s,面积系数β=0.48,计算得到补气洞内风速为59.7 m/s(见图10)。在水位变化过程中,补气洞内风速大小均符合设计规范要求,补气能力需要提高。

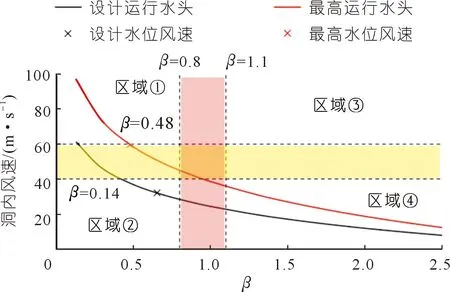
图10 RM水电站补气洞设计合理性评估Fig.10 Design evaluation on performance of air-filling cave in RM Hydropower Station

考虑到补气洞补气能力,建议将补气洞面积增大到42.8 m2,在设计水位下运行时的补气洞内风速为28.3 m/s。同时,最高水位运行时风速为54.2 m/s,且补气能力同样有所提升。

6 结 语

本文对RM水电站补气洞内空气流场进行了数值模拟,并建立了风速的预测公式。结果表明:适当增大补气洞面积是提高空气流畅性和减小风速的有效手段;所构建的拟合公式对风速的预测误差小于10%,能较好地预测补气洞风速。结合相关规范对风速的要求,对锦屏一级水电站泄洪洞和RM水电站放空洞的补气洞设计进行了合理性评估,并提出了相应建议。