一种分裂形式CPR 格式在欠解析流动中的稳定性研究

贾斐然，朱华君，严 红，燕振国，*，石京昶

(1.西北工业大学 动力与能源学院，西安 710000；2.空气动力学国家重点实验室，绵阳 621000)

0 引言

计算流体力学（Computational Fluid Dynamics,CFD）是一种通过数值手段研究流体力学问题的方法，是对理论研究和实验研究的补充。近些年来，为了对流动问题进行精细模拟，高阶格式因其数值耗散误差和色散误差小的特性，逐渐成为CFD 中的一个重要研究方向[1]。

重构修正过程（correction procedure via reconstruction,CPR）方法的思想最早由Huynh[2]提出，当时称之为通量重构（flux reconstruction,FR）方法。Huynh 将其用于求解结构网格上的双曲守恒律方程，王志坚等[3-4]将此方法进行了推广，提出适用于非结构网格的提升配点惩罚法（lifting collocation penalty formulation,LCP），这两种方法联系紧密，被统称为CPR 方法[5]。CPR 方法的优势主要在于三个方面：第一，在求解线性标量方程时，通过调整修正函数类型，CPR 方法可以恢复成间断伽辽金（discontinuous Galerkin,DG）[6]、谱差分（spectral difference,SD）等方法[7]，但不同于DG 方法在求解过程中涉及非线性项的积分，CPR 方法是差分型方法，计算量小且计算复杂度低；第二，CPR 方法对复杂边界有很好的适应性，便于推广到非结构网格[8]；第三，该方法具有良好的紧致性，便于进行并行计算[9]。

CPR 方法或DG 方法在求解非线性问题时，即使流动中没有出现像激波这样的不连续性情况，也可能会由于离散非线性对流项引起的混淆误差的累积而引发稳定性问题[10]。这类问题在欠解析流动中尤为突出。为了增强欠解析流动模拟的稳定性，目前主要存在的稳定机制有滤波[6]、过积分[11]以及分裂形式[12]。

Gassner 等[13]研究了高阶DG 离散在欠解析湍流模拟中的精度，发现低阶近似显示出难以接受的数值离散误差，而高阶离散受混淆误差的影响，往往是不稳定的。对流项中的非线性项使得相对较低波数的模态相互非线性叠加，产生较高波数的模态，甚至是当前基函数无法描述的模态。高于Nyquist 波数的未分辨波数被“混淆”到分辨波数范围。Blaisdell 等[14]在谱方法中提出一种分裂形式，发现其减少了高波数范围内的混淆误差，Gassner 和Abe 等[10,12,15]将这种思路推广到DG 和CPR 方法中。Gassner 等[12]构造了一种高阶分裂形式间断伽辽金谱元法（discontinuous Galerkin spectral element method,DGSEM）框架，并对无黏Taylor-Green 涡（TGV）算例进行模拟，结果表明，与标准格式相比，这种新的分裂形式在求解欠解析湍流涡主导的流动时增强了模拟的稳定性。Winters 等[15]研究高阶DG 方法在欠解析湍流计算中的精度和稳定性，考虑无黏TGV 来分析DG 方法在极高雷诺数下进行隐式大涡模拟（implicit large eddy simulation,ILES）的能力。为了抑制混淆误差，采用过积分[13]和分裂形式两种方法对控制方程进行离散，并比较了这两种方法在无黏TGV 算例中的表现，结果表明，分裂形式具有更好的稳定性。Chan 等[16]将高阶熵稳定DG 格式用于求解欠解析流动，这种采用LG（Legendre-Gauss）点并经过熵投影的格式具有很好的鲁棒性，与采用LGL（Legendre-Gauss-Lobatto）点的高阶熵稳定DGSEM 格式[12]相比，能够分辨尺度更小的流动结构。

CPR 方法在欠解析流动中的研究相比于DG 方法较少。Ball 和Jameson 研究了两种新的高阶FR 格式[17-18]即优化能量稳定通量重构（optimized energy stable flux reconstruction,OESFR）和优化通量重构（optimized flux reconstruction,OFR）在粗网格上求解黏性TGV 的能力，并与能量稳定通量重构（energy stable flux reconstruction,ESFR）方法进行了比较。结果表明，OFR 格式精度最高，所计算的能谱与参考能谱吻合得最好，且在高波数下优于ESFR 方法的能谱。Abe 等[10]针对可压缩Euler 和Navier-Stokes（NS）方程，构造并证明了一种稳定且守恒的FR 格式。这种格式采用LGL 解点，对对流项采用分裂形式，基于多项式分析严格推导了满足离散守恒和动能保持性质的充分条件，通过黏性TGV 算例证明：基于这种分裂形式的FR 框架，使用无耗散动能保持（kinetic energy preservation,KEP）通量[19]，在非常高阶（p15）和相对粗糙网格下的模拟仍然是稳定的。Abe 提出了一种基于LG 点的满足离散守恒律的分裂形式CPR 格式，但并未研究其求解欠解析流动的特性。

Ramírez 等[20]提出了一种通用的子单元限制策略来构造鲁棒的高精度节点DG 格式，主要思路是构造兼容的低阶有限体积（FV）离散，并与高阶DG 进行凸混合。这种策略可以有效处理强激波，在KPP 问题[21]、湍流和高超声速Euler 模拟，及以激波和湍流为特征的MHD 问题上有很好表现。Zhu 等[22–24]针对基于LG 点的CPR 方法，提出了一类先验子单元限制格式。首先，利用激波侦测器检测存在间断的问题单元；然后，将问题单元分解为非均匀子单元，每个子单元包含一个解点；最后，对光滑单元使用CPR 方法计算，对问题单元使用紧致非均匀非线性加权（compact nonuniform nonlinear weighted,CNNW）插值格式计算。这种新策略在分辨率和激波捕捉鲁棒性之间具有良好的平衡。

分裂形式CPR 格式在欠解析流动中的研究较少，且主要以LGL 点作为解点。本文研究了以LG 点为解点的分裂形式CPR 格式在欠解析流动中的应用。首先，对比了基于LG 点的分裂形式和散度形式在求解欠解析流动时的稳定性，展现了分裂形式在增强格式稳定性方面的优势；其次，从分辨率和稳定性的角度比较了LG 点和LGL 点分裂形式CPR 格式；最后，首次将基于LG 点的分裂形式CPR 格式与Zhu 等提出的CNNW 子单元限制格式相结合，求解含激波的Kelvin-Helmholtz 不稳定性问题。

1 控制方程与数值方法

1.1 控制方程

考虑守恒形式的三维N-S 方程：

式中，U为守恒变量，F、G、H分别为x、y、z方向的无黏通量，Fv、Gv、Hv分别为x、y、z方向的黏性通量，具体形式如下：

式中，ρ 为密度，u、v、w分别为x、y、z方向的速度，p为压力，E为单位质量流体的总内能。本文只涉及理想气体，比热比 γ=1.4。黏性应力满足：

式中，µ为动力黏度。

1.2 高阶CPR 格式

本小节以一维守恒形式Euler 方程为例，介绍CPR 格式的构造方法。守恒方程形式为：

计算域 [a,b]，首先将其剖分为N个区间，将其中第j个区间设为Ij=[xj-1/2,xj+1/2],j=1,·,N。为 了便于讨论，将每个区间映射到标准单元I=[-1,1]上。假设每个区间Ij上的点x到标准单元I的点 ξ存在一个线性映射关系：

式中，xj=(xj-1/2+xj+1/2)/2 是区间Ij的中心，hj=xj+1/2-xj-1/2为区间Ij的长度。

在区间Ij上定义K个解点xj,k，k=1,·,K，解点上对应的守恒变量为Uj,k，k=1,·,K。为了便于分析，本文对所有区间均采用相同类型的解点，即LG 点或LGL 点。设标准单元上的解点位置为 ξk，k=1,·,K，则区间Ij上的解点位置由下式计算得到：

由解点处的守恒变量Uj,k，k=1,·,K，通过构造K-1 次Lagrange 插值多项式来逼近Uj：

其中lk(ξ)是Lagrange 插值基函数，形式如下：

同理，区间Ij上的通量函数由下式逼近：

通量多项式Fj(ξ)的构造只依赖于区间内部的解点通量值，在相邻区间交界面处的通量值不连续，即Fj(1)≠Fj+1(-1)。因此，需要构造一个连续通量多项式表达式为：

式中，gL、gR为边界的左右修正函数，满足：

修正函数的形式一般有以下三种：

式中，PK是K阶Legendre 多项式。gDG、gGa和g2分别是可将CPR 格式恢复成DG 格式、SD 格式和Huynh 型格式的修正函数[2]。

为了保证相邻区间交界面处的连续性，需要引入Riemann 通量常用的Riemann 通量有局部Lax-Friedrichs（LLF）、Roe 通量[25]等。

最后，得到Euler 方程的半离散形式：

针对上式，本文使用三阶TVD Runge-Kutta 格式[26-27]进行时间离散。以上为一维CPR 格式的实现过程，二维及三维CPR 格式可以直接由一维形式扩展而来[10,22]。

1.3 分裂形式CPR 格式

同样以一维Euler 方程为例（计算坐标下），分裂形式[10]是将方程中的对流项分裂成守恒形式和非守恒形式的组合，其一般形式为：

式中，P为压力项，将单独处理，不会被分裂。

常用的分裂形式类型有Fe 分裂[28]、Bl 分裂[14]、KG1 分裂[29]和KG2 分裂[29]等。本文只考虑第一种分裂形式，表达式为：

其中，ϕ={1,u,H}T。式（21）中的 (Split)C可由式（22）代替。

(Split)C表示分裂形式下重构通量（通量散度）的ξ方向导数。首先，使用解点处的守恒变量值计算解点处分裂形式的通量散度项。在第n个单元上，假设符号函数 {fn,gn,hn} 代表 {ρ,u,ϕ}，则式（22）中等号右端项在解点处可由以下形式表示：

式中，引入符号ISP;K[ψn] 表示一个任意的函数 ψn的K阶多项式近似：

式（23）的第一项可写为：

因此，解点处分裂形式的重构通量散度项计算如下：

Abe[10]证明了以LGL 点作为解点时，Fe 分裂形式满足离散守恒律。同时也指出：如果以LG 点作为解点，要使分裂形式满足离散守恒律，需要对边界通量项进行修正，形式如下：

式中I[ϕ] 即为ISP;K[ϕ]。

1.4 子单元限制和激波侦测器

本文所使用的子单元限制策略的主要思想是，利用激波侦测器侦测出流场中存在的大梯度或间断的单元，并将其标记为问题单元，然后将这些问题单元划分为非等距子单元，每个子单元包含一个解点，最后在子单元上添加限制手段，具体限制方式在文献[24]中给出。光滑单元用分裂形式CPR 格式计算，而问题单元则使用二阶CNNW 格式计算以捕捉激波。值得注意的是，基于LG 点的分裂形式与子单元限制结合时并不直接满足离散守恒律，仍然需要对分裂形式使用边界通量修正，在2.1.2 小节对此进行了数值验证。

本文采用的激波侦测器为最高模态衰减（highest modal decay,MDH）。该方法利用解多项式的最高模态能量系数在光滑区域衰减较快、非光滑区域衰减较慢的特点[30]，通过设置阈值来判断单元内是否存在大梯度或间断。为了避免奇偶效应，Hennemann 等[31]使用最高和次高模态系数改进了此方法，本文采用这一改进方法。

2 数值测试

使用一维Sod 激波管、二维对流等熵涡[22]问题来测试格式的离散守恒律和数值精度；使用二维欠解析旋涡流动[32-33]和三维黏性TGV[10,18]算例来测试格式的稳定性；使用二维无黏Kelvin-Helmholtz 不稳定性算例来测试分裂形式结合子单元限制技术的激波捕捉能力。为了便于描述，所测试的计算方案按以下方式命名：对流项-解点类型-修正函数-无黏通量。例如，Div-LG-gDG-Roe 表示对流项采用散度形式、解点选择LG 点、修正函数选择gDG、无黏通量选择Roe 通量。表1 列出了本文所采用的算例及其对应的计算条件设置。此外，对于黏性通量，均使用BR2 格式[34]。

表1 算例类型及对应的计算条件设置Table 1 Simulation cases and the corresponding calculation condition settings

2.1 离散守恒律及精度测试

2.1.1 Sod 激波管

Sod 激波管问题计算域为 0 ≤x≤1，被划分成等距的200 个网格。初始条件如下：

该算例存在精确解[35]。左右边界施加Dirichlet边界条件，计算时间T=0.2，CFL=0.1。解多项式阶为p2（即三阶空间精度），总自由度为600。为了便于评估数值稳定性，不采用任何激波捕捉方法。

图1 是使用LG 点和修正函数g2的计算结果。图1（a）表明：基于LG 点的分裂形式CPR 格式直接求解Sod 激波管问题时，并不能正确计算激波位置，即不满足离散守恒律。图1（b）是经过边界通量修正[10]后的计算结果，此时散度形式和Fe 分裂形式均能满足离散守恒律。

图1 T=0.2时Sod 激波管问题的密度分布.修正采用LG 点、g2 修正函数和Roe 通量，总自由度为600(p2)Fig.1 Density profiles of the Sod shock tube problem at T=0.2:(a) without boundary flux fix;(b) with boundary flux fix.LG points,g2 correction function and Roe flux are used,and the total number of DoFs is 600(p2)

2.1.2 对流等熵涡

对流等熵涡问题除了可以用来验证格式的离散守恒律[22]外，还可以用于测试精度。该算例是在一个均匀流动的基础上添加一个等熵旋涡扰动。均匀流动设置如下：

计算域 [-10,10]×[-10,10]，边界均为周期边界，CFL=0.1，计算时间T=0.1。

首先用该算例测试离散守恒律。全局离散守恒律误差表达式如下：

其中，q可以用于表示 ρ、ρu等守恒变量，下标“0”表示初始时刻的守恒变量。

表2 给出了对流项的不同形式在使用LG 点时的离散守恒律误差，其中Div-subcell 和SplitFe-subcell分别表示结合子单元限制的散度形式和分裂形式CPR 格式。当离散守恒律误差接近机器零时，认为格式满足离散守恒律。由表2 可知，当分裂形式与子单元限制相结合时，也需要经过边界通量修正才能满足离散守恒律。

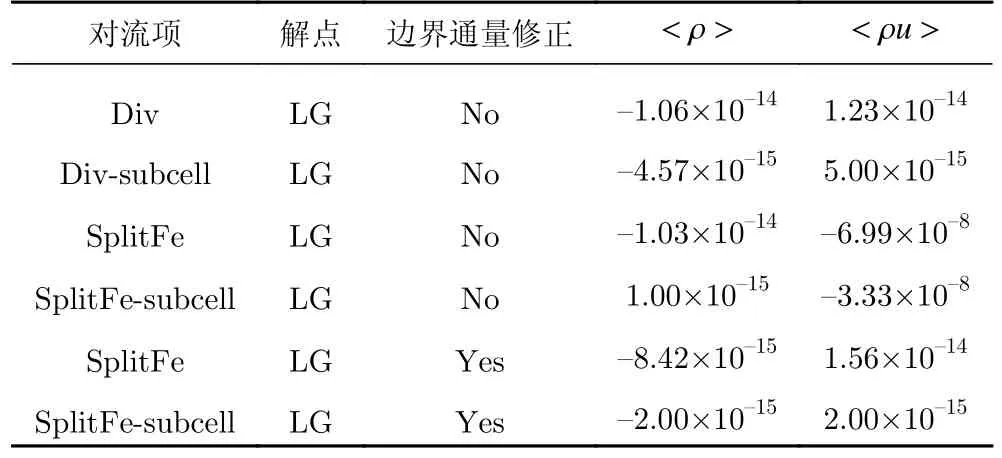
表2 对流等熵涡的全局离散守恒律误差Table 2 Errors of the global discrete conservation law in the computation of convecting isentropic vortex

表3 和表4 分别是基于LG 点的散度形式和Fe 分裂形式的精度测试（p4）结果，这两种对流项形式计算的误差与收敛阶基本相同。表5 和表6 则是基于LGL 点的散度形式和Fe 分裂形式的精度测试（p4）结果，Fe 分裂形式的L1误差小于散度形式，而L∞误差大于散度形式。最后对比表4 和表6，发现基于LG 点的格式误差明显小于LGL 点（接近一个量级）。

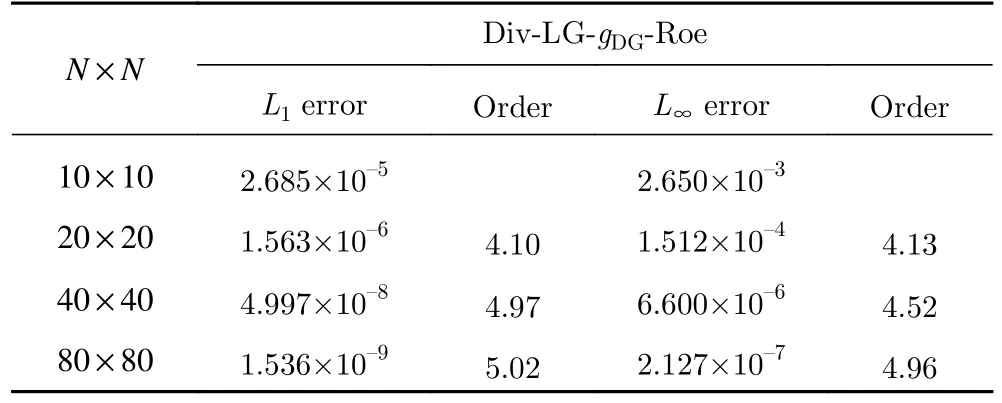
表3 基于LG 点的散度形式精度测试(p4)Table 3 Accuracy test of divergence form based on LG points (p4)

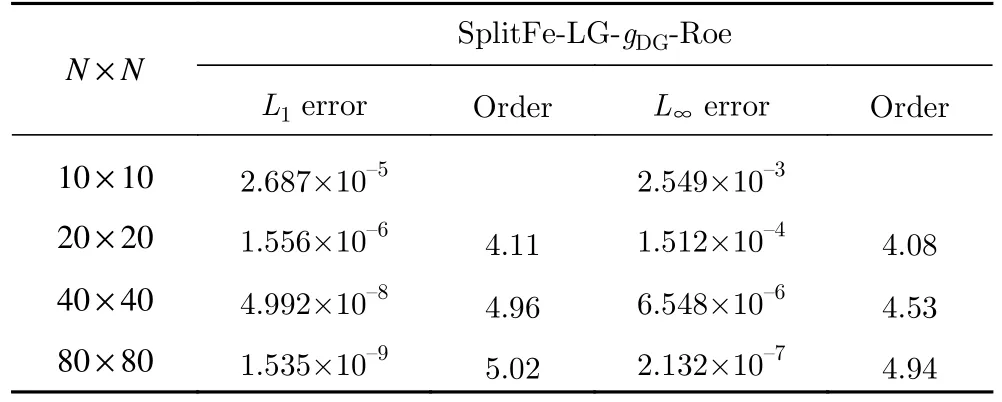
表4 基于LG 点的Fe 分裂形式精度测试(p4)Table 4 Accuracy test of the Fe split form based on LG points (p4)

表5 基于LGL 点的散度形式精度测试(p4)Table 5 Accuracy test of the divergence form based on LGL points (p4)

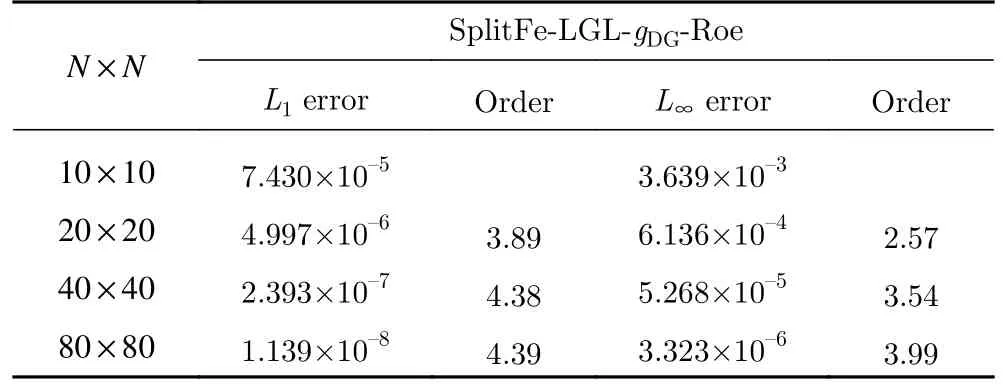
表6 基于LGL 点的Fe 分裂形式精度测试(p4)Table 6 Accuracy test of the Fe split form based on LGL points (p4)

2.2 稳定性测试

2.2.1 欠解析旋涡流动

为了评估格式对实际流动的欠解析模拟的影响，使用二维可压缩Euler 方程和非定常流入边界条件，模拟涡流沿下游传播的被动发生器。该问题是无黏的，使用Euler 方程来研究数值方法在黏性消失极限（极高雷诺数）下的性质和行为[15,36]。算例设置如下：

计算域为 [0,20π]×[-π,π]，计算网格数 120×12，CFL=0.5，T=150.0 。在y=±π位置施加壁面边界条件，x=0位置施加流入边界条件：

式中，ρ∞=1、u∞=1是自由流密度和均匀流速度，是自由流静压，用于通过声速c∞=u∞Ma-1定义流动的参考马赫数。此外，入口处扰动参数定义为A=1/2、K=5、Ω=1，出口边界为初始条件与出口边界相同。T=20π左右时，流场将达到渐近状态。

本算例使用的多项式阶为p5。主要考虑三种CPR格式中常见的Riemann 求解器，即HLL 通量[37-38]、Roe 通量和LLF 通量。在本算例中，在多项式高阶和欠解析条件下，Riemann 求解器会有不同的特性。本算例中选择马赫数为0.03，因为在低马赫数下，会放大HLL 和LLF 通量产生的伪反射和数值噪声，从而更好地展现数值不稳定性带来的影响[32]。除了使用多种Riemann 求解器外，还使用两种不同对流项形式的CPR 格式（散度形式和Fe 分裂）和两种解点类型（LG 点和LGL 点）。为了评估这些方面的影响，考虑流场中的涡量分布

图2 给出了在Roe 通量下，采用不同对流项形式和不同解点的涡量计算结果。所有情况均能稳定计算至结束。比较图2 中的第一和第三小图，发现采用LG 点对流场中的微小结构捕捉得更清楚。

图2 基于Roe 通量，不同对流形式和解点下的涡量场比较：LGL 点，散度形式；LGL 点，Fe 分裂形式；LG 点，散度形式；LG 点，Fe 分裂形式Fig.2 Comparison of the vorticity fields computed with different convention from and solution point combination based on the Roe flux:LGL points,Div form;LGL points,SplitFe form;LG points,Div form;LG points,SplitFe form

图3 是在LLF 通量下的涡量计算结果。值得注意的是，散度形式下LGL 点和LG 点分别在T=15.66和T=56.84时崩溃，因此没有画出其涡量分布。这是由于LLF 通量在靠近出口边界处会产生伪反射（图中被红圈圈出的），这些伪反射与传入的旋涡非线性相互作用，导致小尺度噪声，使得计算不稳定。此外，即使存在明显的小尺度噪声，分裂形式均能稳定计算到T=150。

图3 基于LLF 通量和Fe 分裂形式、LGL 和LG 解点下的涡量场Fig.3 Comparison of the vorticity fields computed with the LGL and LG solution points based on the LLF flux and Fe split form

图4 是在HLL 通量下的涡量计算结果。值得注意的是，散度形式下LGL 点和LG 点分别在T=15.56和T=50.23时崩溃，因此没有画出其涡量分布。两种分裂形式均能稳定计算到T=150。

图4 基于HLL 通量和Fe 分裂形式、LGL 和LG 解点下的涡量场Fig.4 Comparison of the vorticity fields computed with the LGL and LG solution points based on the HLL flux and Fe split form

2.2.2 黏性Taylor-Green 涡

在本小节中，我们模拟了黏性TGV 问题。该问题通常用于研究旋涡动力学和湍流转捩与衰减[39]。该问题由最初包含光滑涡量分布的立方体流体组成，能够反映数值格式的鲁棒性以及对多尺度流动结构的模拟能力。在美国航空航天学会航空航天科学会议[40]上举行的计算流体动力学高阶方法国际研讨会上，该算例用于评估湍流模拟方法。许多作者已经成功使用高阶模拟方法预测该流场[13,18,41-42]。本文将使用TGV 来比较散度形式和分裂形式在湍流欠解析模拟中的精度和稳定性。初始条件设置如下：

其中，马赫数和雷诺数分别设为0.1 和1 600，L为参考长度。计算域是 -πL≤x,y,z≤πL，被划分为互不重叠的均匀六面体单元。在本测试中，包括内部解点在内的自由度总数固定在 643左右，以便在不同阶的解多项式之间进行比较。表7 列出了网格数与解多项式阶的对应关系。计算时间为 0 ≤T≤20，使用固定时间步长 ∆t=3.14×10-4。本算例只考虑了Fe 分裂形式。为了更好地描述该问题随时间的演化过程，需要定义以下几个参数：

表7 总单元数和解多项式阶数Table 7 Total number of cells and order of the solution polynomial

式中，u为速度矢量，ω为涡量矢量。

图5 分别给出了不同时刻下，多项式阶为p3 的方案SplitFe-LG-g2-Roe 的z方向涡量等值面图。从T=0开始，初始流场存在明显的大涡结构，随后不断地拉伸和旋转，逐渐破裂成较小的涡结构[43]。

图5 不同时刻黏性Taylor-Green 涡 z 方向涡量等值面图Fig.5 Iso-surfaces of vorticity in z-direction for the viscous Taylor-Green vortex at different time instances

2.2.2.1 多项式阶数的影响

为了节省计算资源和比较格式的稳定性，本算例的计算均是在欠解析即网格数量不足条件下进行的。我们从p1 开始，逐渐提高多项式阶数，直到出现不稳定解。如图6 所示，可以明显看出：在保证总自由度不变时，提高多项式阶数使得数值解逼近参考解，这与COX 之前的结论一致[44]。本文主要关注的是欠解析情况下格式的非线性稳定性问题。当多项式阶数提高时，在T=5 时流场很容易由于混淆误差而崩溃，这时就需要具有去混淆效果的分裂形式来增强格式的稳定性。

图6 总自由度约为 643时，采用Div-LG-g2-Roe 方案的动能、动能耗散率、拟涡能计算结果Fig.6 Computational results of the Div-LG-g2-Roe scheme with the total degree of freedom of 643: (a) kinetic energy;(b) kinetic energy dissipation rate;(c) enstrophy

2.2.2.2 对流项形式的影响

图6 和图7 对比了方案Div-LG-g2-Roe 和方案SplitFe-LG-g2-Roe。在图6 中，多项式阶从p1 到p4 的方案均能稳定计算至T=20，而当阶数提高到很高阶（p7）时，方案在T=5左右崩溃。而图7 中，所有多项式阶的方案均稳定。这一结果表明，即使是很高阶（p8）离散，分裂格式CPR 格式仍能保证数值稳定性。

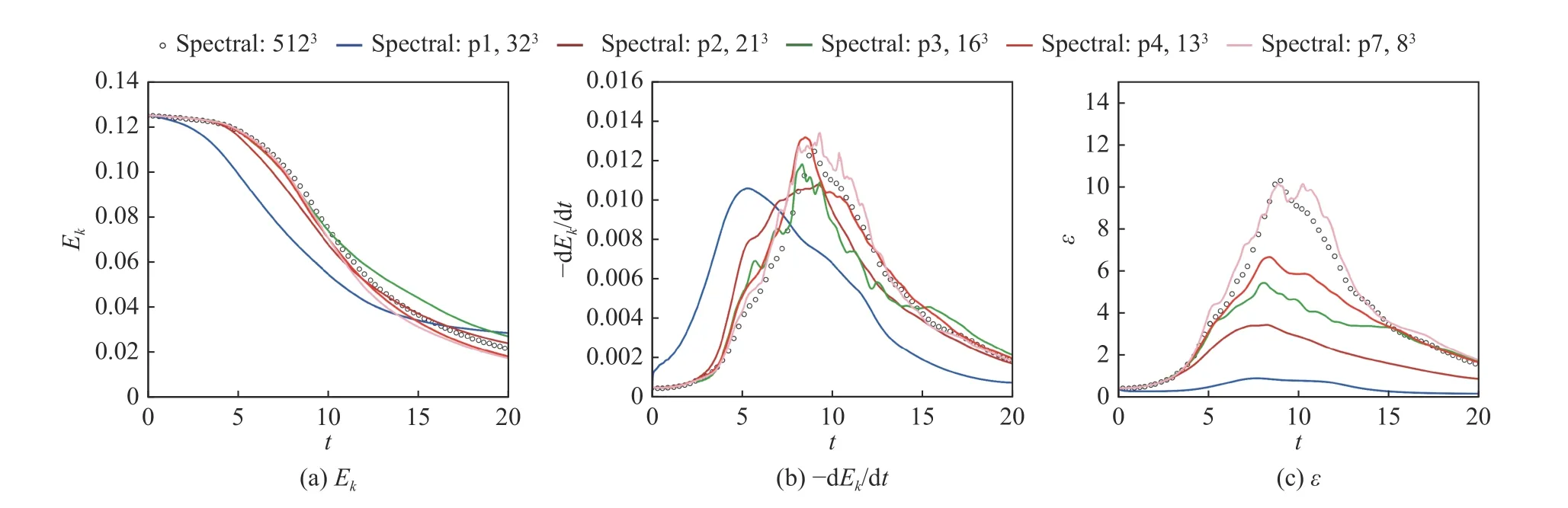
图7 总自由度约为 643时，采用SplitFe-LG-g2-Roe 方案的动能、动能耗散率、拟涡能计算结果Fig.7 Computational results of the SplitFe-LG-g2-Roe scheme with the total degree of freedom of 643: (a) kinetic energy;(b) kinetic energy dissipation rate;(c) enstrophy

图8 和图9 是基于LGL 点的散度形式与分裂形式的对比，与LG 点所得结论一致，分裂形式极大地提高了格式的稳定性。

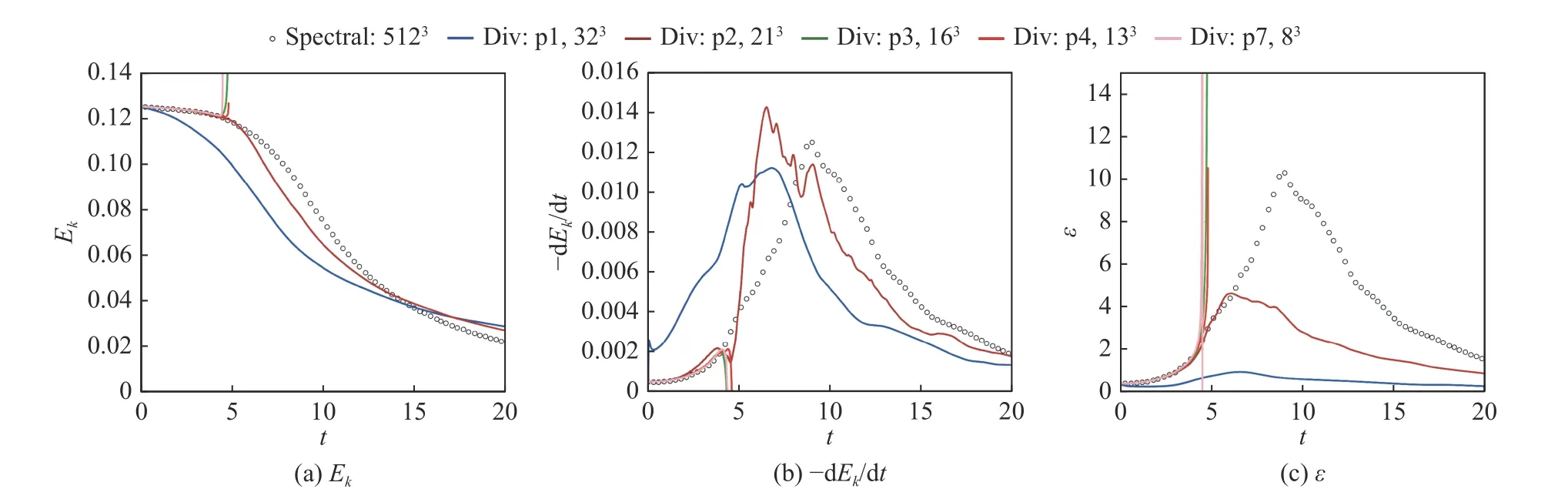
图8 总自由度约为 643时，采用Div-LGL-g2-Roe 方案的动能、动能耗散率、拟涡能计算结果Fig.8 Computational results of the Div-LGL-g2-Roe scheme with the total degree of freedom of 643: (a) kinetic energy;(b) kinetic energy dissipation rate;(c) enstrophy

图9 总自由度约为 643时，采用SplitFe-LGL-g2-Roe 方案的动能、动能耗散率、拟涡能计算结果Fig.9 Computational results of the SplitFe-LGL-g2-Roe scheme with a total degree of freedom of 643: (a) kinetic energy;(b) kinetic energy dissipation rate;(c) enstrophy

2.2.2.3 解点类型的影响

如图6 和图8 所示，首先对比散度形式下LG 点和LGL 点的计算结果。LG 点在p1～p4 方案下稳定，而LGL 点仅能在p1～p2 方案下稳定。因此，这一结果表明，在多项式阶不是很高的条件下（p5 以下），基于LG 点比基于LGL 点的散度形式CPR 格式稳定性更优。

图7 和图9 是分裂形式下LG 点和LGL 点的计算结果。两种解点类型均能在所要求的多项式阶下保证稳定。从图7（c）和图9（c）可以看出，LG 点相较于LGL 点的优势在于：其计算精度更高，尤其是多项式阶为p7 时，LG 点的拟涡能与参考解吻合得更好。

2.3 激波捕捉能力测试

本小节考虑二维无黏Kelvin-Helmholtz 不稳定性问题[45]。该算例对于CPR 方法来说很具有挑战性，因为它包含严重欠解析的涡结构，马赫数约等于0.6。本测试的目的是将结合子单元限制技术的分裂形式CPR 格式应用于求解欠解析流动。初始条件由下式给出：

其中B=tanh(15y+7.5)-tanh(15y-7.5) 。计算域[-1,1]2且均为周期边界。我们使用 64×64个四边形单元对计算域进行均匀划分，多项式阶数为p7，计算时间T=10。

在图10 中，我们分别绘制了T=3.7 和T=10时分裂形式结合子单元限制求解Kelvin-Helmholtz 不稳定性问题的密度等值线。在使用相同激波侦测器和相同自由度的情况下，相比于Ramírez 等[20]提出的基于LGL 点、结合子单元限制技术的DGSEM 格式的计算结果，这种新策略能分辨更多的小尺度特征且振荡更少。图11 分别给出了两个时刻下的问题单元分布。

图10 不同时刻下Kelvin Helmholtz 不稳定性模拟的密度云图Fig.10 Density contours for the Kelvin Helmholtz instability simulation at different time instances

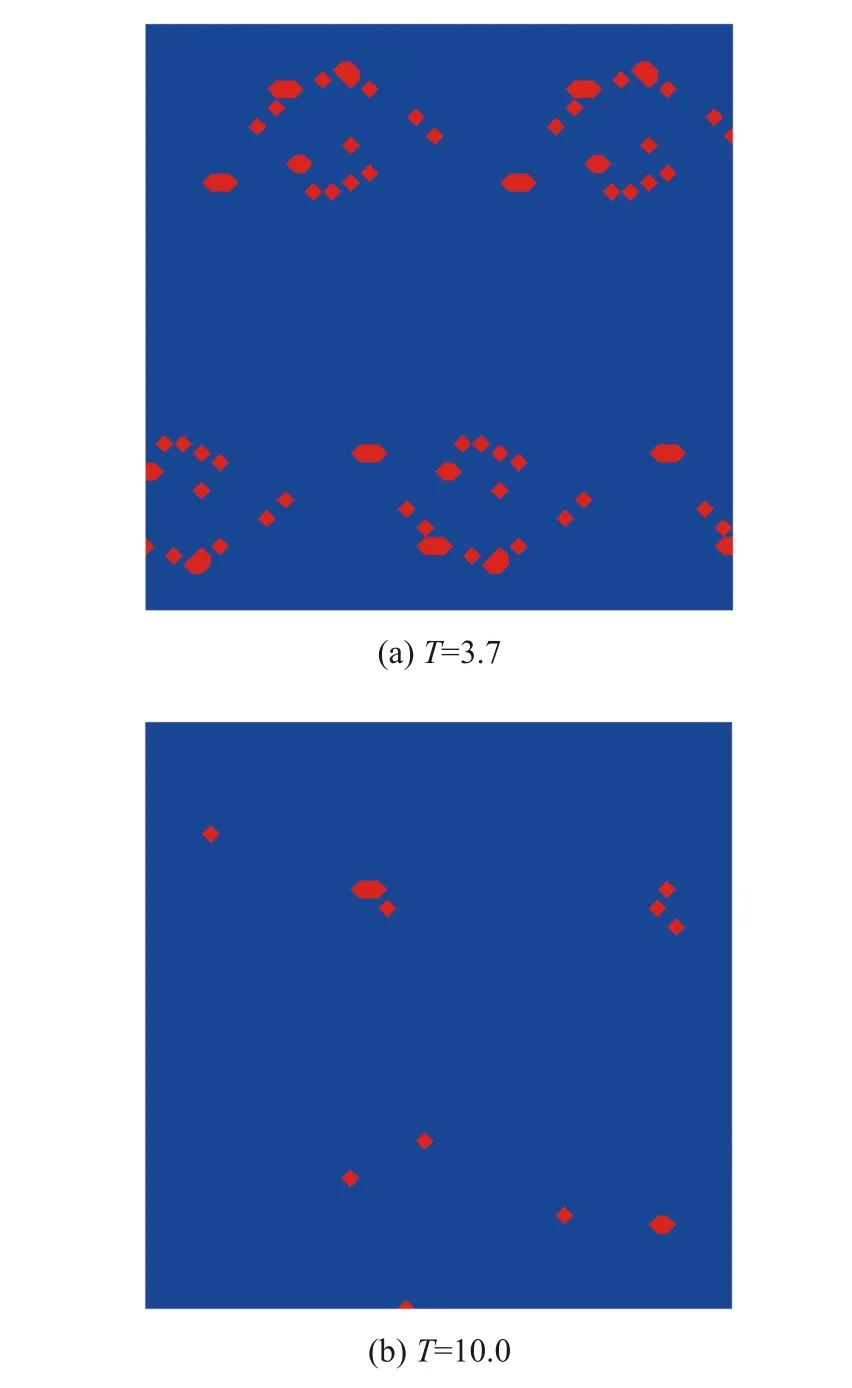
图11 不同时刻下Kelvin Helmholtz 不稳定性模拟的问题单元分布Fig.11 Distribution of problematic cells for the Kelvin Helmholtz instability simulation at different time instances

3 结论

本文在CPR 格式的基础上，比较了采用不同解点类型的分裂形式对求解欠解析流动时的稳定性和精度的影响，主要有以下结论：

1）Sod 激波管和等熵涡算例结果表明，以LG 点作为解点时，通过边界通量修正的Fe 分裂形式满足离散守恒律。

2）精度测试结果表明，使用LG 点的散度形式和分裂形式的L1、L∞误差基本相同；在相同散度形式或分裂形式下，使用LG 点的误差明显小于LGL 点（约一个量级）。

3）二维欠解析旋涡流动算例用来考察数值通量的特性和格式的稳定性。LLF 和HLL 通量在出口边界处会产生伪反射和小尺度噪声，导致散度形式CPR 格式在计算时崩溃，而Fe 分裂形式能够保证稳定计算。Roe 通量则能完全抑制这种伪反射。此外，使用LGL 点时放大了出口处产生的伪反射，而LG 点对流场中的微小结构捕捉得更清楚。

4）三维黏性Taylor-Green 涡算例结果表明，无论采用LG 点或LGL 点，即使是很高阶（p7）的离散，分裂形式CPR 格式对于保证计算稳定依然是有效的，且LG 点精度更高，在p7 下与参考解匹配得更好。如果统一使用散度形式，在多项式阶不是很高的条件下（p5 以下），采用LG 点的格式稳定性优于LGL 点。

5）二维无黏Kelvin-Helmholtz 不稳定性算例考察了分裂形式结合子单元限制技术的激波捕捉能力，相比于基于LGL 点的间断谱元法子单元限制策略，前者在分辨率和稳定性方面均有优势。

总的来说，本文将基于LG 点的分裂形式CPR 格式用于求解欠解析流动问题，不仅能提高格式的稳定性，而且相比于LGL 点，该方法对流场的分辨率更高；在结合子单元限制策略后，其对含激波的欠解析流动也能得到很好的解。本文基于CPR 方法、采用“分裂+LG”策略时需要采用边界通量修正保证守恒性，如果想将这一策略应用于其他高阶谱元方法，在如何满足格式的守恒性方面有待进一步探索。