基于RVSM 运行需求的波纹度影响分析方法
2024-01-09艾梦琪马玉敏张彦军
艾梦琪,马玉敏,张彦军,2,*
(1.航空工业第一飞机设计研究院,西安 710089;2.西北工业大学 航空学院,西安 710072)
0 引言
缩小垂直间隔最低标准(reduced vertical separation minimum,RVSM)是指在飞行高度8 900 m 到12 500 m之间,飞行器的垂直间隔标准从600 m 降低到300 m,从而大幅增加空域的飞行高度层数[1]。实行RVSM可以改善空域饱和造成的航线延误等问题,有利于更加合理规划、使用空域资源,在确保空中交通安全条件下,提升航空运输的经济效益[2-3]。
因此,飞行高度测量的准确性是飞机RVSM 运行能力适航取证重点关注的内容[4]。飞机飞行时一般利用静压孔或静压探头测量压力值进行高度解算,获得实时的飞行高度。当静压源附近蒙皮存在波纹度时会对静压测量产生影响,进而影响高度测量[5-7]。以巡航马赫数0.74 的B737 飞机为例,在10 km 高度飞行时,静压压力系数0.001 的测量偏差会导致直接解算高度2.5 m 的误差。因此,主流民机均对静压源附近的蒙皮提出了波纹度限制,如B737NG 飞机要求主静压口周向76.2 mm 范围内不允许出现波深超过0.508 mm 的波纹度,以控制由波纹度导致的高度测量误差在28.96 m 以内[3,8]。
由于工艺条件的限制,蒙皮波纹度几乎是不可避免的,因此需要建立合理的分析方法对其影响进行评估,以指导飞机高度测量误差的分配以及静压源误差修正(static source error correction,SSEC)曲线的确定。由于蒙皮表面的波纹度具有尺度小、随机分布的特点,对其影响的准确模拟存在一定困难。国外公开的相关研究成果十分有限,国内则随着国产大飞机的问世与发展,开始针对性地进行了一些探索。现有研究多以按区域分块的直状波为研究对象[9],能够反映一定规律,但波纹模型与真实情况差异性较大;评估方法以计算流体力学(Computational Fluid Dynamics,CFD)数值计算为主[10-11],计算所需的时间成本较大且评估精度缺少系统的试验结果验证。因此,为了推动相关工程问题的解决,一方面需要结合工程问题的实际需求,发展工程可用的快速评估手段,在研究初期进行一些辅助分析,大大减少时间成本;另一方面需要根据蒙皮波纹度的常见形态,开展典型波纹度的原理性试验研究,建立经验证的CFD 计算方法,为大量评估计算及SSEC 曲线的确定提供支撑。
本文以常见的蒙皮波纹度形态和参数构造了简化的波纹度模型,建立了基于小扰动理论的快速分析方法,在一定精度范围内实现了压力影响的快速评估;结合国内首次波纹度原理性试验结果,验证了所采用的CFD 数值计算方法的准确性。
1 波纹度定义
波纹度表征物体表面相较于理想设计表面的中等尺度的外形偏差,是介于宏观尺度的形状误差和微观尺度的粗糙度之间的物理量,表现为表面轮廓围绕设计轮廓的不规则的凹凸偏差。在获得理论表面和实际表面后,可通过波长、波幅、波纹度值等参数分析波纹度,如图1 所示,虚线为理论面,实线为实际面,A、B 分别为两个波峰,C 为波谷,定义L为波长,d为波幅,d/L为波纹度值。根据测量数据统计分析,加工制造、装配中的各类偏差和使用中造成的飞机蒙皮波纹度的波长约在50~500 mm 范围,波幅一般不超过1 mm,波纹度值的量级约在1×10-3[12-14]。

图1 波纹度定义Fig.1 Definition of waviness
考虑到蒙皮波纹度的随机分布特性,进行基于RVSM 运行需求的波纹度研究时,往往将波纹度简化为典型的状态,通过对一些特殊波形、定量波幅和波长的波纹度模型的研究,分析波纹度对表面压力分布的影响规律,发展并验证用于波纹度影响计算的高精度方法,进而为实际蒙皮的高度测量误差分析提供参考。
2 基于小扰动假设的快速分析方法
2.1 方法介绍
由于蒙皮波纹度尺度很小,对流场的影响可以按小扰动进行处理,因此将定常势流理论的控制方程进行线性化处理并增加压缩性修正,可以得到基于小扰动假设的波纹度表面计算模型,通过求解简单的线性方程对波纹度的影响进行快速分析。
假设波纹度壁面的函数为f(x),亚声速条件下小扰动速度势函数 ϕ满足的小扰动方程和壁面及远场边界条件为[15]:
将壁面函数进行傅里叶级数展开:
其中a0、an、bn为傅里叶变换系数。采用分离变量法求解上述方程,将级数形式的壁面函数代入方程,可得:
将速度势函数表示的流场速度带入压力系数表达式,并进行小扰动展开,忽略高阶小量,可得到小扰动压力系数为:
由此可得波纹度壁面的压力分布计算式:
2.2 计算结果
以凸波为例,构建如图2 所示的5 种典型的波纹度壁面,假设波长为100 mm,波幅0.1 mm,即波纹度值0.001,流场的马赫数为0.7,采用上述方法对壁面的压力系数进行快速计算,得到的压力分布如图3 所示。

图2 不同波形示意Fig.2 Schematic of different form of waviness

图3 不同波纹度的压力系数分布Fig.3 Pressure coefficient distribution of waviness
上述5 种类型的波纹可分为两组:正弦波、圆弧波、抛物线波的压力分布为单凹曲线,正弦波在波峰处压力影响量相对更大,由于波纹度很小,圆弧波和抛物线波压力系数分布基本重合;余弦波和样条波的压力系数分布曲线外形相似,前后缘附近存在极值点,样条波的中心波峰处压力影响量略大于余弦波。
采用快速分析方法计算不同波形的波峰处压力系数随马赫数的变化情况,结果如图4 所示(抛物线波与圆弧波相近,不再展示),统一波长为100 mm,波纹度值为0.001。随马赫数增大,压力系数绝对值增加;相同马赫数下,样条波的压力系数绝对值最大,圆弧波的最小。从图5 看出马赫数0.7 下,不同波形的波峰处压力系数值随波纹度值呈线性变化,但斜率并不相同,其中样条波斜率最大,圆弧波斜率最小。
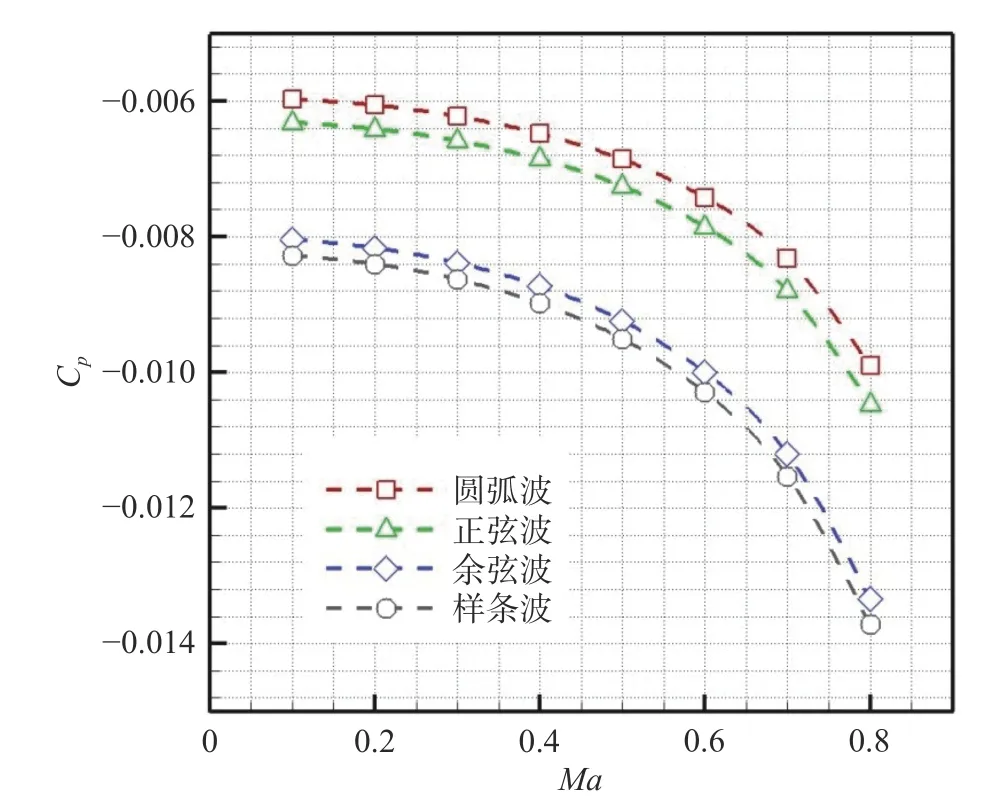
图4 峰值点压力系数值随马赫数的变化Fig.4 Pressure coefficient of peak point with different Mach number
3 CFD 数值方法
3.1 数值方法介绍
CFD 方法通过对流场域和控制方程进行离散化,将复杂的流场解算过程转换为空间离散点处求解近似流场参数的代数方程,可以在一定的精度范围内模拟流场的细节特性,获得较为精准的流场信息。对于具有随机分布且外形不规则波纹度的飞机蒙皮,合理的CFD 方法可以清晰地获得蒙皮表面的压力分布情况。
本文采用的数值计算方法以雷诺平均N-S 方程作为控制方程,采用格心格式的有限体积法对控制方程进行离散,其中黏性项的空间离散采用二阶中心差分格式,无黏项则采用二阶Roe 迎风通量差分格式离散,时间项采用隐式LU-SGS(lower-upper symmetric Gauss-Seidel)双时间法推进。湍流模型采用SST 模型,同时采用多重网格技术加速计算收敛。经验证,计算方法具有良好的收敛性和鲁棒性。
3.2 计算模型
以中心布置有典型三维波纹度的平板壁面作为蒙皮波纹度研究的简化模型(图6),中心圆盘为具有不同波纹度值的圆弧波、样条波及样条多波的旋成体模型,如图7 所示。为减小平板边缘对中心区域的影响,平板边界取7 倍圆盘直径,前后缘进行修型设计,计算的远场边界取30 倍平板弦长。

图6 试验模型示意Fig.6 Test model

图7 波纹度模型的波形示意Fig.7 Schematic of waveform of waviness model
采用多块结构网格划分流场域,对重点关注的中心波纹度区域采用O 型网格划分以提高网格质量,并在该区域进行网格加密。生成边界层网格时,保证第一层网格高度满足y+≤1,网格增长率小于1.2,总网格量约为500 万。
3.3 计算结果及验证
以上述模型作为研究对象,在航空工业气动院FL-62 风洞中开展了波纹度影响的风洞试验研究。该风洞为连续式跨声速风洞,在马赫数0.15~1.6 范围内具备良好的流场品质。试验通过在中心波纹度圆盘上表面布置多个测压孔,对不同流场状态下的表面压力数据进行采集,与基准平板数据进行对比分析,获得不同波纹度模型对表面压力分布的影响情况。
3.3.1 数值计算结果验证
图8~图10 分别为样条波、圆弧波和样条多波模型试验和计算得到的中心圆盘区域的表面压力分布云图。来流方向由上至下,模型的波纹度值均为+0.002 5。3 种模型的压力分布形态具有较大差异,其中样条单波模型沿流向压力变化梯度比较均匀,圆弧波模型边缘处压力梯度大,中间区域压力梯度小,多波模型存在3 处压力极值区域。试验结果与计算结果非常相似,由于试验中随机误差等的影响,左右并不完全对称分布。
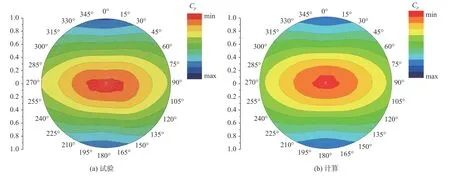
图8 样条波纹度模型压力分布Fig.8 Comparison of pressure coefficient distribution of spline waviness model between experiments and simulations

图9 圆弧波纹度模型压力分布Fig.9 Comparison of pressure coefficient distribution of circular-arc waviness model between experiments and simulations

图10 样条多波模型压力分布Fig.10 Comparison of pressure coefficient distribution of spline multi-waviness model between experiments and simulations
沿流向对称面计算压力分布曲线与对称面上测压孔的试验数据对比如图11 所示,对称面压力分布形态与模型的波形相似,在不同马赫数下试验数据与计算曲线均吻合良好,表明数值计算方法精度较高。

图11 对称面计算压力系数与试验对比Fig.11 Comparison of pressure coefficient of symmetric surface etween experiments and simulations
以样条波纹度模型为例,图12 给出了不同马赫数下波纹度模型中心波峰(谷)处压力系数值随波纹度值的变化曲线。计算和试验结果均表明,中心点压力系数值随波纹度呈线性变化,不同波纹度下,试验结果与计算结果基本重合。

图12 模型中心点处压力系数值随波纹度变化曲线Fig.12 Pressure coefficient of peak point with different waviness
以+0.002 5 样条波纹度模型为例,图13 给出了波纹度模型中心处压力系数值随马赫数的变化曲线。随马赫数增加,波纹度中心的压力系数绝对值增大,两者可用二次函数进行拟合。马赫数较大试验数据与计算结果吻合较好,马赫数较小时试验值略小于计算值,但误差很小,在可接受范围内。
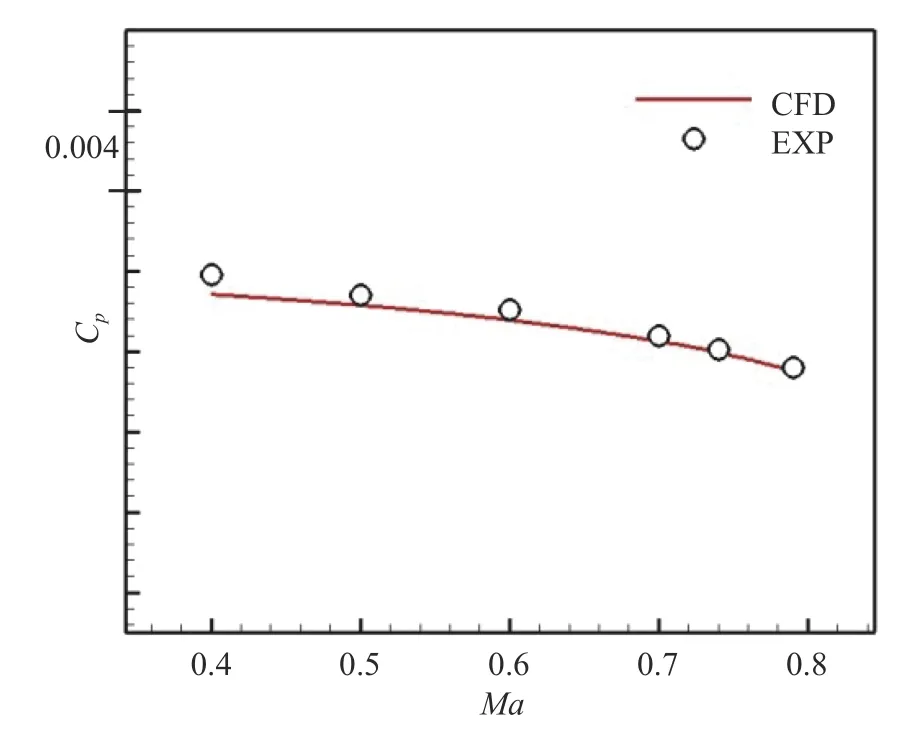
图13 模型中心处压力系数值随马赫数变化曲线Fig.13 Pressure coefficient of peak point with different Mach number
3.3.2 数值计算误差带分析
为获得波纹度模型表面的压力分布情况,试验中在模型表面分散布置了30 个测压孔进行数据采集,根据测压孔的布置情况,提取相应位置的计算压力系数值进行对比,统计计算值相较试验值的偏差量。统计30 个试验状态共计900 个数据点的压力系数偏差,形成了图14 所示的偏差分布直方图。

图14 计算相对试验压力系数偏差分布直方图Fig.14 Histogram of relative deviation distribution of pressure coefficient for computational results in comparing with experiments
根据统计结果,57.5%数据点的压力偏差在±0.000 5以内,77.2%的数据点偏差在±0.001 以内,89.5%的数据点偏差在±0.001 5 以内,97.8%的数据点偏差在±0.002 以内,99.8%数据点偏差在±0.002 5 以内,表明采用的计算方法是合理的,计算精度非常高。
4 快速分析结果的三维修正
基于小扰动理论的快速分析方法采用了无黏无旋的理想流体的假设,加入了压缩性的修正,适用于亚声速下无限展长的二维波纹度壁面压力影响的分析。计算时只需提供波纹度壁面的外形函数及马赫数,就能够较好地获得壁面的压力分布形态及波峰(谷)位置的压力值。如图15 所示,采用CFD 数值方法计算二维样条波壁面模型得到的压力分布形态与快速分析结果基本一致。

图15 快速分析方法与二维CFD 计算结果对比Fig.15 Comparison between fast analysis method and twodimensional CFD calculation results
对飞机蒙皮而言,波纹度往往以鼓包或凹坑的三维形式出现,因此快速分析结果需要进行三维修正。以样条波为例,图16 给出了马赫数0.7 时采用快速分析方法、二维CFD 计算、三维CFD 计算以及风洞试验方法得到的波纹度中心处的压力值的对比。在不同波纹度值下,快速分析结果与二维CFD 计算结果非常接近,且由于CFD 中考虑了流体黏性作用,在正波纹度值时中心压力值的绝对值略大于无黏结果,在负波纹度时中心压力值的绝对值略小于无黏结果。三维CFD 计算结果与试验结果非常接近。采用CFD 计算的二维结果与三维结果呈线性关系,根据拟合分析,三维修正系数约为0.55。
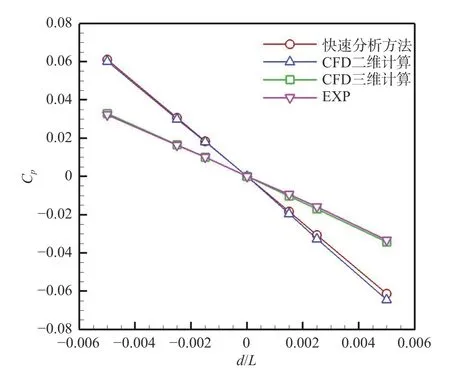
图16 不同方法计算结果对比Fig.16 Comparison of calculation results by means of different methods
采用该系数对马赫数0.4 时波纹度模型的计算结果进行修正,同时将修正系数外推至圆弧波模型,修正值与试验数据的对比情况如表1 所示,误差小于0.001,在工程上可以接受。

表1 三维修正结果Table 1 Three-dimensional correction result
5 结论
本文以典型蒙皮波纹度模型为研究对象,建立了CFD 数值方法和基于小扰动理论的快速分析方法,研究了不同波纹度对压力系数分布的影响规律,得到以下结论:
1)经多状态、多模型测压风洞试验验证,本文建立的数值方法对波纹度表面压力系数的评估精度较高,97.8%的计算压力系数数据与试验结果的偏差在±0.002 以内。该方法可广泛应用于实测外形飞机的静压偏差计算,为RVSM 高度测量偏差分析及静压源误差修正曲线的确定提供一定的技术支撑。
2)基于小扰动理论的分析方法能够对已知波形的规则波纹度表面压力系数进行快速计算,是一种可用于分析飞机静压源附近小尺寸波纹度影响的快速评估手段,具有较高的工程应用价值。本文采用的系数修正方法精度基本满足工程要求,如需进一步提高计算精度,可充分考虑不同工况条件发展更为复杂的修正关系式。
