凹腔对高超声速边界层稳定性的影响

冯 烁，王伯福，涂国华，武健辉，陈坚强，杨 强，*

(1.上海大学 力学与工程科学学院，上海市应用数学和力学研究所，上海 200072；2.空天飞行空气动力科学与技术全国重点实验室，绵阳 621000；3.中国运载火箭技术研究院，北京 100076)

0 引言

层流到湍流的转捩可导致飞行器表面摩阻热流剧烈变化，在高超声速时气动力/热上升3～5 倍，严重影响飞行安全，是制约高超声速飞行器气动设计的重要因素[1]。边界层转捩作为一个复杂的初边值问题，对壁面粗糙度极为敏感。壁面凹陷和凸起是实际飞行器表面常见的粗糙元形式。典型粗糙元依据其形状可以分成凹陷型和凸起型，其中凹陷型又称为凹腔。对于矩形凹腔，宽深比d/h是影响凹腔内流动结构的重要因素之一[2-4]，依据不同宽深比，凹腔对应的流动状态可分为三类：开式凹腔、过渡式凹腔和闭式凹腔。对于闭式凹腔，随着凹腔深度的增加，边界层主层对平均流的修正逐渐增强。当凹腔过渡为开式凹腔时，凹腔的核心区产生由主流边界层和腔内回流区组成的混合层，这种混合层会在凹腔局部产生增长率更快的Kelvin-Helmholtz 不稳定性。Guo 等[5]指出来流条件也是影响腔内流动结构的重要因素之一。Palmer 等[6]发现高超声速边界层在凹腔周围和下游的流动形态与凹腔的几何形状和来流条件密切相关。本文研究了多个宽度、深度的凹腔模型，针对这种密集的尺寸，旧有的分类方法界限模糊，不利于得到定量的数据结论，因此本文研究讨论还是直接使用了尺寸的大小分类。董昊等[7]从几何形状和分布形式两方面对粗糙元的分类进行了较为完整的总结。

粗糙元尺寸对于边界层稳定性起着至关重要的作用。对于孤立表面凸起粗糙元，目前对其控制转捩机理及效果的研究主要集中于粗糙元的几何参数，其中粗糙元高度对转捩效果起着至关重要的作用[8]，当高度改变时，粗糙元边界层的感受性和失稳机制也随之改变。Sumariva 等[9]研究了不同长度、高度和形状的凸起孤立粗糙元引起的转捩提前现象。Brehm等[10]针对粗糙元形状、高度和间距等因素对扰动的演化影响进行了研究，发现存在一个粗糙元高度阈值，低于该阈值的粗糙元对扰动增长的影响很小，与Gaster[11]的结论一致；同时发现形状和间距对二维扰动波的增长具有显著影响。

借助局部散射理论对扰动波控制效果开展定量分析，Wu 等[12]针对较小尺度粗糙元开展研究，发现当粗糙元尺度与不稳定波波长相当时，粗糙元对T-S波起促进作用。李闯和董明[13]采用直接数值模拟研究了局部矩形凹腔对高超声速平板边界层中第二模态扰动演化的影响，发现对于较浅的凹腔，低频第二模态扰动被促进，而高频扰动则被抑制。通常，随着凹腔深度的增加，凹腔对扰动的抑制作用增强，但当凹腔的深度超过某一临界值时，凹腔内流动出现新的失稳机制，且与凹腔内基本流的拓扑结构密切相关。对于浅凹腔，由于前后缘可以独立地看作后向和前向台阶，前后缘分离泡相距较远，相互作用较弱；而对于深凹腔，分离泡会占据整个凹腔，进而引起更多动能向回流区域传递[14]。

粗糙元位置对边界层稳定性也有重要影响。在高超声速边界层中，源于自由流的快、慢声波在向下游演化过程中激发了边界层中的快、慢模态（Mode F、Mode S），二者相速度相同时会出现同步[15]，进而激发Mack 模态[16-17]。快、慢模态发生同步的位置称为同步点。Duan 等[18]研究发现凸起粗糙元位于单频扰动快、慢模态的同步点上游时对扰动起促进作用，而位于同步点下游时则对扰动起抑制作用。Chen、Lee[19]和Zhao 等[20]分别通过实验和数值模拟确认了凹腔和快、慢模态同步点位置的关系，发现影响效果与凸起粗糙元类似。Park 等[21-22]采用抛物化稳定性方程研究了不同形状二维光滑凸起粗糙元对高超声速平板边界层线性不稳定性的影响，也获得了类似的结论。

综上可见，针对凹腔对边界层稳定性影响的局部参数化研究已有较丰富的成果，还需进一步研究凹腔尺寸变化对Mack 模态的全面影响规律。为此，本文将借助线性稳定性理论（linear stability theory,LST）、抛物化稳定性方程（parabolic stability equation,PSE）、高精度直接数值模拟（direct numerical simulation,DNS）和全局稳定性分解（global stability decomposition,GSD）系统分析凹腔对高超声速和超声速边界层稳定性的影响，以期给飞行器设计和转捩控制提供参考。

1 物理模型及计算方法

1.1 物理模型

Fong等[23-24]发现了凸起粗糙元分别位于特定频率（即同步频率）的同步点前后时的扰动波幅值增长变化规律。Zhao、Dong、李斯特等[20,25-26]借助局部散射理论系统研究了粗糙元参数对扰动波演化的影响规律。Han 等[27]针对超声速凹腔做了自激振荡的模态分解。为了更好地与这些相关文献对照补充，本文研究模型为带凹腔的零攻角平板，来流马赫数为Ma=5.92、1.38，与文献[20,23-27]一致，计算工况详见表1。本文重点主要在：1）超声速和高超声速来流条件下的对比；2）更广泛的参数范围；3）大尺度凹腔的全局不稳定性研究。

表1 算例计算工况Table 1 Flow conditions for the simulation cases

为了方便表述，流体变量均基于特征参考量进行无量纲化[28]，对应的有量纲量用上标(●)*表示，参考长度选取为Lref=1.0 mm。计算域和边界条件如图1所示，坐标原点位于平板前缘。

图1 计算域及边界示意图Fig.1 Schematic diagram of the computational domain and boundaries

为减少计算量，计算域流向区间为[x0,xl]=[100,400]，法向高度为Ly=100。左边界为入口条件，给定可压缩Blasius 相似解。右边界为出口边界，采用线性外推，计算扰动演化时，在出口附近采用网格拉伸处理，以消除虚假反射波的影响。上边界采用远场条件。下边界为无滑移无穿透的固体壁面，对于高超声速工况，给定壁温Tw=334.9 K，而对于超声速工况，给定绝热壁面边界，(∂T/∂y)|wall=0。已有研究发现，相对于绝热壁面，等温热壁促进第一模态增长，而抑制第二模态增长，等温冷壁则起相反的作用。在线性增长阶段，不同壁温条件对增长率的影响并不大[29-31]。

本文选取了不同尺寸的凹腔模型开展研究，参数如表2 所示。宽度d/δ99取值0.5、2.0、3.0、4.0、6.0，深度h/δ99取值0.5、1.0、1.5、2.0、2.5、3.0、4.0，其中δ99为凹腔中心位置处的当地边界层厚度。设计算例可分为固定宽度变深度算例组、固定深度变宽度算例组。参照文献[20]，凹腔中心点位置固定在x=185，对于Ma=5.92 和Ma=1.38 工况，对应的当地边界层厚度分别为δ99*=2.36 mm 和δ99*=2.45 mm。为方便描述，当凹腔尺寸小于当地边界层厚度或与当地边界层厚度相当时，称为小尺度凹腔；当凹腔宽度和深度都已明显大于当地边界层厚度时，称为大尺度凹腔，在本文中，当凹腔尺寸满足d/δ99＞6、h/δ99＞3 时，定义为大尺度凹腔。

表2 不同类型凹腔尺寸参数Table 2 Geometry parameters for different types of cavities

1.2 计算方法

本文采用基于LST 和PSE 的线性稳定性分析、DNS 和GSD 三类方法开展凹腔流动分析。流动的控制方程为可压缩Navier-Stokes（N-S）方程，计算采用理想气体状态模型，黏性系数、热传导系数由Sutherland 公式计算给出。对流项采用Steger-Warming通量分裂，在激波附近采用五阶加权紧致非线性格式（weighted compact nonlinear schemes,WCNS）[32-33]，激波以外区域采用六阶迎风格式，黏性项采用六阶中心差分，时间项离散采用具有TVD 性质的3 步三阶Runge-Kutta 法。

采用当地化的线性稳定性分析方法LST 进行稳定性分析，模态解表示形式如式（1）所示：

对于大尺度凹腔，流动在流向也具有较强的非平行性，为此采用Tu 等[36]提出的基于无矩阵的GSD方法开展流动稳定性分析。该方法的思想是通过反复调用CFD 求解器构造原特征矩阵A（m×m维）的子空间S（n≪m）实现降维处理，进而找到工程上最关心的数个主特征值。具体思路如下：

选择一系列线性无关的初始扰动：

通过高精度CFD 工具，让扰动场演化 ∆t时间后得到：

其中矩阵B=exp(A∆t)。可以投影处理构造小矩阵：

其中，Q、R对 应Um的QR分解矩阵，满足Um=QR，且可以证明矩阵S与矩阵A的特征值和特征向量满足：特别地，当采用Arnoldi 方法构造子空间时，GSD 可退化为传统的动态模分解DMD。

1.3 网格收敛性

图2 展示了d2h1H 凹腔附近的网格分布情况，法向每隔4 个网格点显示，流向每隔2 个网格点显示。网格沿法向进行拉伸，边界层内网格数保持在150 以上，以保证近壁区足够的网格分辨率，沿流向对凹腔的前后缘进行加密以准确捕捉此处的波系结构。

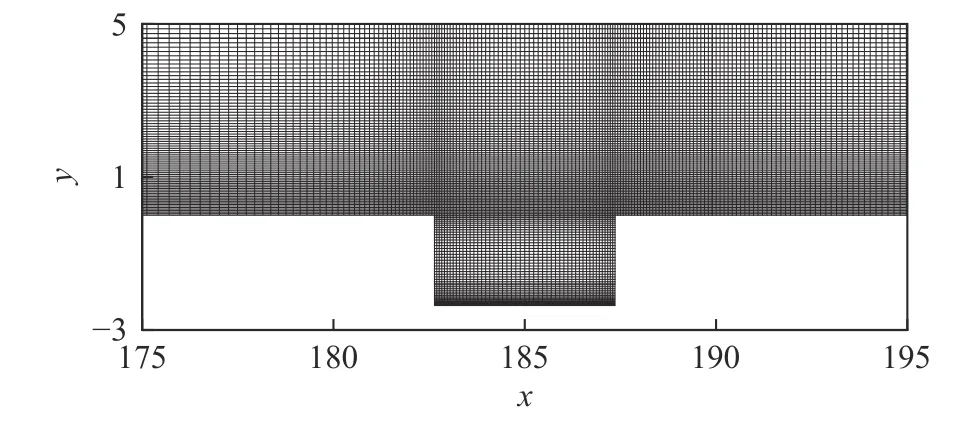
图2 凹腔局部区域网格分布Fig.2 Grid distribution around the cavity

图3 为d6h1.5H 算例加密网格（流向和法向网格数为腔内501×201，腔外 2 001 × 1 001 ）与原始网格（腔内251×101，腔外 1 001 ×501）计算结果对比图。随着凹腔宽度和深度的逐渐增大，腔内网格点数也逐渐增多。为验证计算结果的网格无关性，选取d6h1.5H 算例进行研究，可看到壁面压力系数和压力脉动幅值随流向的演化曲线在流向和法向网格加密前后完全吻合，说明了本文计算结果具有网格无关性。

图3 网格收敛性验证Fig.3 Grid convergence verification

2 基本流特征

入口（x0=100）采用Blasius 剖面以获得计算域内的边界层流场。图4 展示了Ma=5.92 下d2h1H、d2h3H、d6h1H 和d6h3H 算例的基本流特征。

图4 不同凹腔压力云图及流线图Fig.4 Pressure contours and streamlines around cavities

从压力云图可以看出不同尺度的凹腔均呈现类似的波系结构，在凹腔前缘出现膨胀波系，而在后缘出现压缩波系，且二者均随凹腔尺度的增加而增强。从流线图可以清晰地看出凹腔内的涡结构分布：对于d2h1H 算例（图4（a）），凹腔内存在单个稳定的顺时针旋转主涡结构，随着深度的增加（d2h3H 算例，图4（b）），凹腔下底面左右侧开始形成小的角涡结构；随着宽度的增加（d6h1H 算例，图4（c）），主涡结构被拉长，后缘涡强度高于前缘涡强度，但前后缘不对称性减弱。对于较大尺度凹腔d6h3H，上述涡结构特征变化更为明显（图4（d）），凹腔内呈现复杂的多涡系结构。

图5 展示了Ma=1.38 时d6h3S 算例的非定常流动状态。定常情况下Ma=1.38 的波系结构与Ma=5.92的高超声速情况类似，当固定宽度增加深度或者固定深度增加宽度时，凹腔前缘膨胀波均增强，后缘开始出现明显的压缩波，并且凹腔内部的角涡范围明显增大，内部回流区流动变得复杂。从图5 可见凹腔内发生自激震荡并在下游形成规律性周期振荡，表明大尺度凹腔结构自身引起的绝对不稳定性变得重要。

图5 d6h3S 算例凹腔不同时刻的|∇ρ|Fig.5 Density gradient |∇ρ| contours around d6h3S at different time instances

图6 和图7 展示了凹腔宽度固定时，变深度组凹腔不同站位的速度型和壁面处速度剪切沿流向的变化。从速度型剖面可以看出，凹腔前站位速度型与Blasius 相似解吻合较好，离开凹腔很快又恢复到相似解（图6）。Ma=1.38 超声速情况下（图6（b）），凹腔附近速度型与高超声速情况类似，但凹腔前缘膨胀波较弱，前缘壁面速度型吻合度更高。相比于凸起粗糙元，凹腔对下游边界层的基本流修正要弱得多[20]。由于凹腔内部分离泡结构的存在，速度型在凹腔内存在较大差异。随着凹腔深度的增加，流向速度在凹腔顶部剪切层附近（y=0）单调增加，但是由于腔内回流区的存在，流向速度先减小到负值再回到凹腔底部壁面处的零值。

图6 变深度组凹腔流向速度剖面对比Fig.6 Streamwise velocity profiles for cavities with different depths

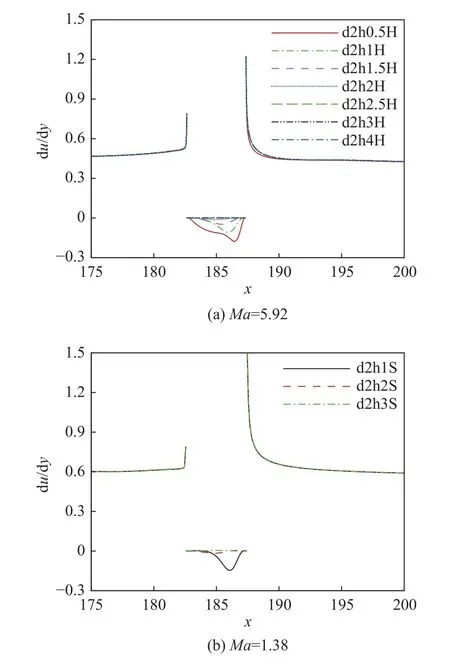
图7 变深度组凹腔壁面处速度剪切特征对比Fig.7 Wall shear rates for cavities with different depths

对于壁面处速度剪切（见图7），在接近凹腔前后缘时剪切突增，表明前后缘附近流速突然增加，后缘附近明显大于前缘。小深度的回流区中心靠近右侧壁面，并且随着深度增加逐渐向前缘移动，但是当深度增加到2 倍边界层厚度（图7（a））时，再增加凹腔深度不再有明显的剪切极值。相比于高超声速情形，超声速来流下（图7（b））凹腔内部壁面处剪切剖面仅存在单峰结构且峰值更加明显，说明回流区更加集中于凹腔后缘。

图8（a、b）展示了Ma=5.92 下固定宽度组和固定深度组凹腔内壁面压力系数分布。如图8（a）所示，在凹腔前部，随着深度从0.5δ99（d2h0.5H 算例）开始逐渐增大到4δ99（d2h4H 算例），负压区大小变化很小；而在凹腔内部，浅凹腔（d2h0.5H 算例）产生了较强的逆压梯度，且随着深度增加逆压梯度逐渐减弱。如图8（b）所示，随着宽度的增加（由d0.5h1H 算例到d6h1H 算例），前后缘局部压力极值增大，凹腔前部区域拥有更广的负压区，这说明凹腔宽度增加导致了前后缘的压力修正进一步增强。图8（c、d）展示了Ma=1.38 的情况，值得注意的是，超声速情况下腔内逆压梯度明显减弱。

图8 变深度和变宽度凹腔壁面压力系数Cp 对比Fig.8 Comparison of wall pressure coefficient Cp for cavities with varying depths and widths

经过以上DNS 分析，获得了不同凹腔对基本流的影响规律，下文将进一步通过稳定性分析手段研究凹腔对边界层稳定性特征的影响。

3 非定常扰动演化

3.1 入口扰动选取

已有研究表明，凹腔安装位置相对同步点位置而言对边界层稳定性具有重要影响[14,19,22,37-38]。图9给出了Ma=5.92、x=185 站位的快慢模态相速度随频率的变化，可以看出快慢模态在ω=0.98（对应的频率时相速度相等，发生同步，演化曲线与文献[20]的结果一致。

图9 Ma=5.92、x=185 站位的快慢模态相速度随频率变化曲线Fig.9 Phase velocity variations with frequency for fast and slow modes at Ma=5.92 and x=185

图10（a）给出了本文研究的Ma=5.92 平板边界层的中性曲线（图中蓝色空心圆圈代表快慢模态同步点站位），可见第一模态的上支界与第二模态的下支界重合，平板前缘很快进入稳定性理论分析得到的不稳定区间。图10（b）给出了Ma=1.38 工况的中性曲线，由于来流马赫数较低，仅出现第一模态，未出现稳定性理论预测的高阶Mack 模态。

图10 平板边界层中性曲线Fig.10 Neutral curves for flat-plate boundary layers

针对Ma=5.92 时的凹腔尺寸，选取了7 个典型的不稳定频率，即ω=0.30、0.53、0.76、0.98、1.07、1.14 和1.45，对应的有量纲频率、同步点流向站位及无量纲扰动波稳定性特征参数见表3。可见，不稳定波频率越高，对应的同步点越靠近上游，其中最低频的两个扰动（40 kHz 和70 kHz）对应的同步点流向站位已超出计算域。

表3 Ma=5.92 时入口扰动波参数Table 3 Parameters for the inlet disturbance wave at Ma=5.92

对于Ma=1.38，由于不存在同步点，并且其不稳定区间较窄，因此选取凹腔中心站位处最不稳定频率ω=0.095 附近的三个典型频率开展分析，具体参数如表4 所示。计算域入口不稳定波形状函数由LST 求解得到。

表4 Ma=1.38 时入口扰动波参数Table 4 Parameters for the inlet disturbance wave at Ma=1.38

3.2 凹腔对边界层线性稳定性的影响

图11 展示了Ma=5.92 来流条件下平板、基准凹腔（d2h1H 算例）、深凹腔（d2h3H 算例）和宽凹腔（d6h1H 算例）对应的扰动增长率云图。结果表明，凹腔对于增长率的影响较为局部，且大尺度凹腔的局部影响更为显著，但增长率在凹腔下游均重新恢复到指数增长形式。图12展示了Ma=1.38 来流条件下的基准凹腔（d2h1S 算例）和宽凹腔（d6h1S 算例）对应的扰动增长率云图，可见增长率在凹腔附近被局部促进，并且随着凹腔宽度增大促进效果也增强。

图11 Ma=5.92 来流下不同尺寸凹腔的边界层扰动增长率云图Fig.11 Growth rate contours for boundary layers with different sizes of cavities at Ma=5.92

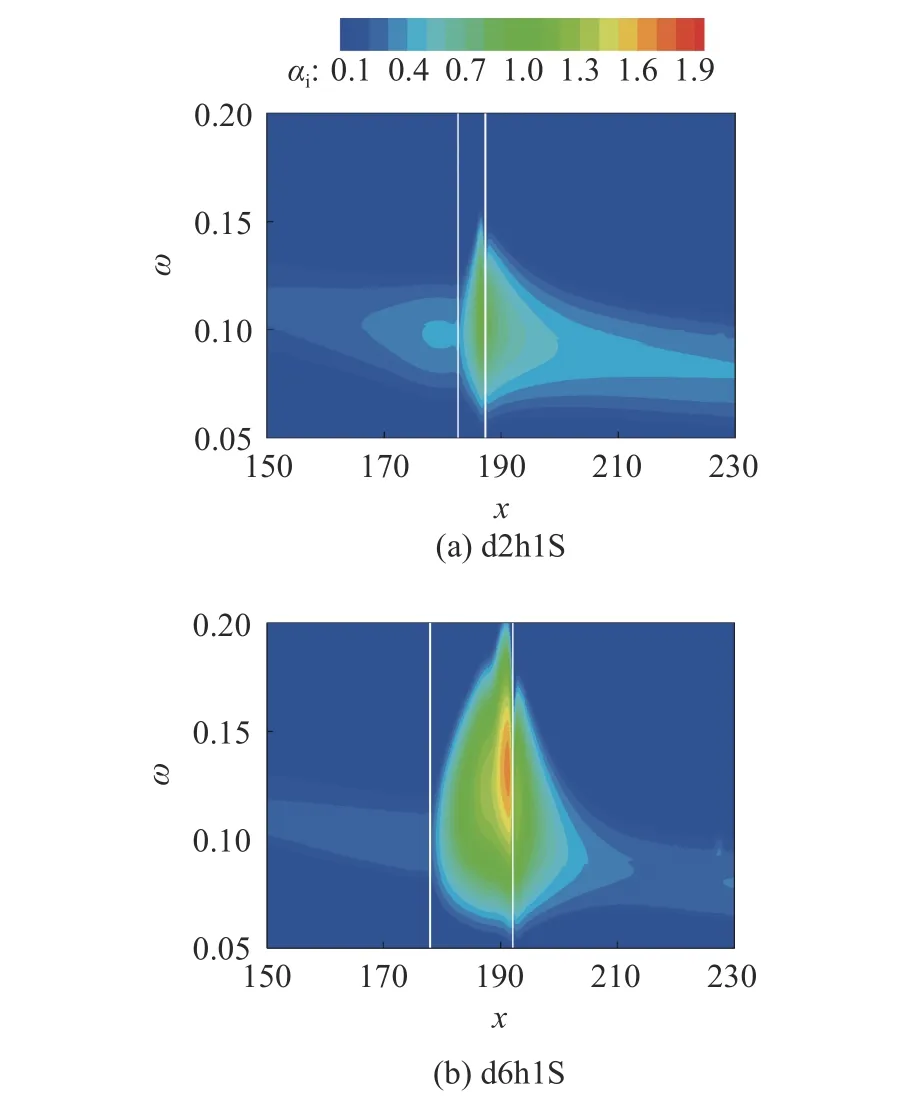
图12 Ma=1.38 来流下不同尺寸凹腔的边界层扰动增长率云图Fig.12 Growth rate contours for boundary layers with different sizes of cavities at Ma=1.38

由于凹腔附近局部非平行性较强，采用传统的基于当地化假设的一维线性稳定性理论（LST）进行稳定性预测误差较大，接下来我们将采用DNS 和GSD 方法研究凹腔内部流动的稳定性（3.2.1～3.3 节内容）。但是此处我们关注的重点是凹腔的上游和下游，在稍远离凹腔的位置流动非平行性影响比较小，图11 和图12 主要展示的是凹腔对不同频率扰动在不同流向站位的影响的整体画面，也可以给读者带来凹腔附近增长率畸变的宏观感受。

3.2.1 凹腔位置影响

图13 展示了Ma=5.92 来流下扰动同步点附近两个频率扰动波（ω=0.53、1.07）经过凹腔d2h1H 的扰动演化瞬时压力场。可以看到扰动波穿过凹腔前缘的膨胀波时发生了强烈的畸变，且高频扰动能更快地恢复到压缩波前的状态。扰动波能直接传入凹腔内部，但对于同一流向站位，凹腔内扰动与凹腔外扰动存在约180º相位差。

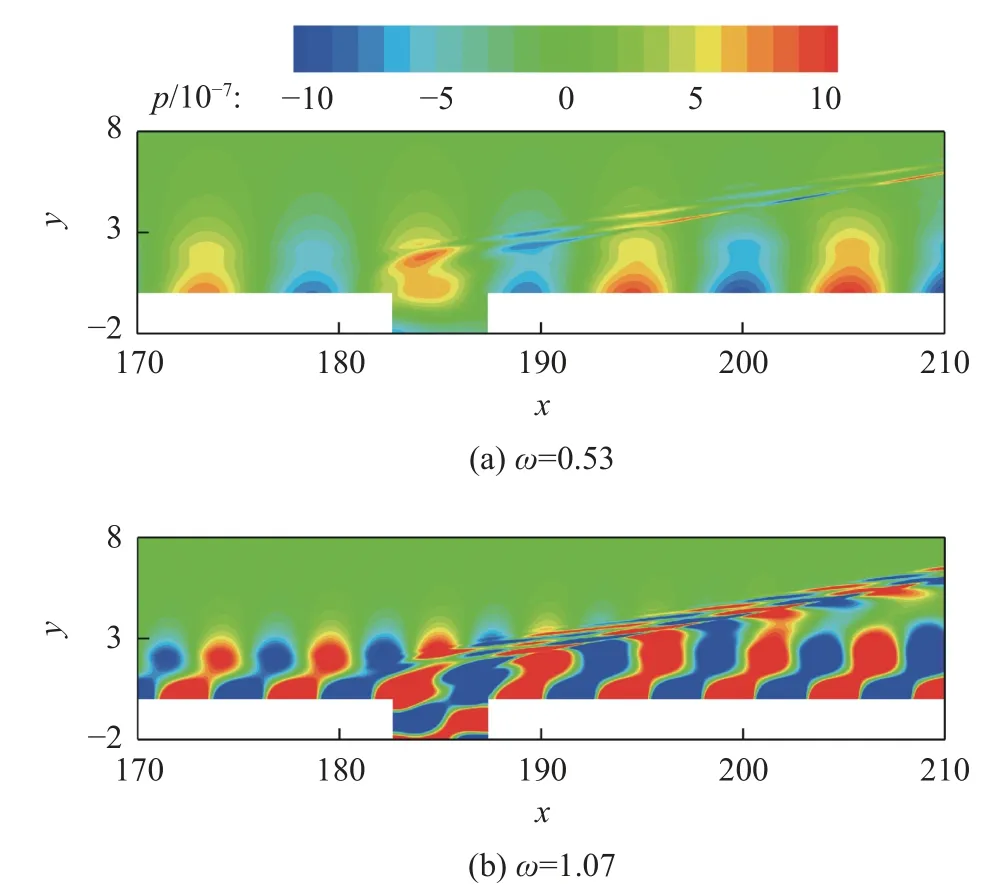
图13 Ma=5.92 来流下不同频率扰动波经过凹腔d2h1H 的瞬时压力脉动场Fig.13 Instantaneous pressure fluctuations around d2h1H at Ma=5.92 for disturbance waves with different frequencies

图14 展示了Ma=1.38 来流下最不稳定频率附近两个扰动波（ω=0.07、0.12）经过凹腔d2h1S 的扰动演化瞬时压力场。与Ma=5.92 情况类似，扰动在经过凹腔上方时向势流区传播，但相比于高超声速情况，膨胀波和压缩波波角更大，压缩效果更弱。

图14 Ma=1.38 来流下不同频率扰动波经过凹腔d2h1S 的瞬时压力脉动场Fig.14 Instantaneous pressure fluctuations around d2h1S at Ma=1.38 for disturbance waves with different frequencies

图15 进一步展示了高超声速算例d2h1H 中扰动在带凹腔平板上的幅值演化曲线。图中绿色实线为DNS 计算得到的压力脉动包络，粉色虚线为LPSE 预测结果，灰色阴影区对应凹腔安装位置。由图可见，线性抛物化方程（LPSE）在扰动的初始发展阶段能较好地预测扰动幅值沿流向的增长。对DNS 获得的压力脉动采用Hilbert 函数提取幅值包络[39]，可以发现，扰动在凹腔前呈指数增长，在凹腔处产生复杂的波动，在凹腔下游又迅速恢复至近似指数增长。这说明凹腔处局部突变对扰动波的影响范围有限。为此，我们引入Wu 等[12]提出的局部散射理论中的透射系数ℜ来定量描述凹腔对扰动波和转捩过程的影响：

其中，xf是凹腔下游透射系数 ℜ趋于常数定值时的流向站位，Ap(xf) 是xf站位处压力脉动幅值的法向最大值，下标“0”对应光滑无凹腔情形。当 ℜ＜1时，表示凹腔对扰动波起抑制作用，且其值越接近于0 抑制作用越强；当 ℜ＞1时，表示凹腔对扰动波起促进作用，其值越大表明促进效果越明显。

小尺度凹腔情形的透射系数与扰动的增长率云图可以直接关联。在凹腔尺寸比较大时，此时凹腔下游扰动增长率误差较大，透射系数仅能依靠扰动演化的DNS 结果换算出来。

图16 显示了高超声速工况下凹腔同步点附近三个不同频率扰动波的透射系数随凹腔尺寸的变化情况。可见，不同尺寸的凹腔在同步频率ω=0.98 附近对扰动波的抑制效果最佳。凹腔对扰动波的透射系数与凹腔宽度和深度并非呈完全单调。观察不同宽度凹腔的透射系数分布可以发现，随着宽度的增加，凹腔对其上游同步频率扰动的促进作用逐渐增强，而对凹腔附近同步频率扰动的抑制作用也逐渐增强。并且对于大宽度、小深度的宽浅腔d4h0.5H 和d6h1.5H算例，其在同步点附近的抑制效果更为突出。图17展示了Ma=1.38 的三个典型工况d2h1S、d4h3S 和d6h2S算例对应的透射系数随着扰动波频率的变化。在所考察的频率范围内，凹腔一直促进扰动波的增长，并且促进效果随频率升高逐渐增强。这一结果与高超声速情况下凹腔对低频扰动的作用效果类似（图16）。

图16 Ma=5.92 来流下凹腔同步点附近不同频率扰动波的透射系数随凹腔尺寸的变化Fig.16 Variations of correction coefficients with different sizes of cavities at Ma=5.92 for disturbance waves with different frequencies near the synchronization point of the cavity

图17 Ma=1.38 来流下三个典型工况对应的透射系数随扰动波频率的变化Fig.17 Variations of correction coefficients with different disturbance wave frequencies at Ma=1.38 for three typical cases

考虑到宽度和深度变化时流动特征变化显著，因此需要进一步进行尺寸参数化研究。

3.2.2 凹腔尺寸影响

针对Ma=5.92 来流条件，我们将凹腔中心点固定在频率为ω=0.98 扰动波的同步点位置（x=185），进一步研究凹腔的尺寸变化对扰动演化的影响。图18 展示了ω=0.98 的入口扰动波经过表2 中4 个典型凹腔的瞬时压力脉动场。可以看到，随着凹腔深度和宽度的增加，扰动波穿透进凹腔并形成复杂的波系结构。扰动波在凹腔前缘被拉伸，而在凹腔后缘则被压缩，并沿凹腔底部法向形成反射波。当凹腔宽度显著大于扰动波波长时（如图18（c）），可以观察到法向反射波基本垂直于腔体壁面，并与入射波形成90°波角。

图18 Ma=5.92 来流下扰动波（ω=0.98）经过不同尺度凹腔的瞬时压力脉动场Fig.18 Instantaneous pressure fluctuations for the disturbance wave with ω=0.98 passing through cavities at Ma=5.92

图19 展示了来流Ma=1.38 下ω=0.095 的入口扰动波经过3 个典型凹腔的瞬时压力脉动场。结果表明，随着凹腔深度和宽度的改变，凹腔上方势流区传播的扰动逐渐增强，并且相对于深度的增加，宽度的改变对下游边界层扰动传播影响更大。

图19 Ma=1.38 来流下扰动波（ω=0.095）经过不同尺度凹腔的瞬时压力脉动场Fig.19 Instantaneous pressure fluctuations for the disturbance wave with ω=0.095 passing through cavities at Ma=1.38

由于凹腔位于同步点位置附近时抑制效果最佳，选择展示Ma=5.92、ω=0.98 工况下不同尺寸凹腔的扰动系数云图（图20），图中星号表示4 个典型凹腔算例：d2h1H、d2h3H、d6h1H 和d6h3H。可以进一步将参数区间分成三个区域：左侧区域（d/δ99＜2）的小宽度凹腔抑制效果最弱；右下角区域（d/δ99＞2，h/δ99＜1.5）的大宽度小深度凹腔抑制效果最好；右上角的大宽度大深度凹腔区域次之。图中最优凹腔尺寸为宽浅腔d6h0.5H 算例，达到了近40%的扰动幅值抑制效果。总体而言，凹腔深度不变，抑制扰动幅值的效果随凹腔宽度单调增强；而固定宽度增加深度的抑制效果并非单调变化的，这与较小尺度下的凹腔深度变化规律类似[13]。当凹腔深度增加时，腔内分离泡充满整个区域，继续增加深度反而产生了额外的促进作用。

图20 Ma=5.92、ω=0.98 工况下不同尺寸凹腔透射系数云图Fig.20 Correction coefficient contours for cavities with different sizes at Ma=5.92 and ω=0.98

对于高超声速来流，扰动波频率ω=0.98 时，扰动透射系数随凹腔宽度d变化规律如图21（a）所示：随着宽度逐渐增加，扰动波抑制效果逐渐增强，且在(d/δ99,h/δ99)=(6,1)时达到最佳扰动幅值抑制效果近35%。扰动波抑制效果随凹腔深度h变化如图21（b）所示：宽度较小时，随着深度的增加，抑制效果变化不明显；当宽度d达到4 倍当地边界层厚度时，随着深度增加，抑制效果出现较大的非单调波动。对于超声速来流，扰动波频率ω=0.095 时，随着凹腔宽度的增加，促进效果逐渐增强（图21（c））；随着凹腔深度的增加，促进效果变化不明显，对于宽腔（d/δ99=4 和6）甚至出现了促进效果减弱的现象（图21（d））。最终研究发现，大宽度凹腔对扰动波幅值的控制效果（抑制或促进）均优于小宽度凹腔。

图21 扰动波的透射系数随凹腔尺寸变化Fig.21 Variations of correction coefficients with different sizes of cavities

3.3 凹腔自激不稳定性

当凹腔尺度达到一定阈值后，如Ma=1.38 来流下的d6h3S 算例，凹腔内开始出现自激振荡，给下游边界层引入新的扰动源，将触发新的转捩机制。考虑到凹腔内部的强非平行性，本节采用GSD[36]开展分析。采用Gavish 和Donoho[40]提出的基于渐近分析的最优截断秩，通过判断奇异值最优截断，筛除掉非物理的模态。所获得的特征谱如图22 所示。图23 展示了4 个典型的GSD 模态的空间分布（图22 中M1、M2、M3 和M4），对应的频率分别为ω=0.033、0.073、0.106 和0.140。可以发现不同模态扰动分布的集中区域不同，如剪切层区域主要由M1 和M2 模态主导，尾迹区主要由M1 模态主导且扰动分布类似Mack 模态。同时凹腔内部还出现了新的扰动形式，如M3 模态。M4 模态的扰动能量也主要集中在凹腔上方的剪切层区域，但能量幅值较弱。凹腔上方存在向下游传播的声波，近壁面处存在行进波，与亚声速凹腔流动结果类似[41]。

图22 凹腔流动d6h3S 的全局稳定性特征谱Fig.22 Eigen spectrum for the global stability of the cavity flow d6h3S

图23 典型主导模态形状函数Fig.23 Modal shapes of typical dominant modes

图24 展示了DNS 流场中凹腔尾迹区域和前缘近壁区域采样点，即(x,y)=(196.6,0.7)和(x,y)=(179.3,-4.9)处的流向速度时间序列及对应的傅里叶频谱。可见，凹腔的尾迹区中存在较强的单频主导扰动，频率为ω=0.035，与GSD 的M1 模态接近；而在凹腔的前缘近壁区除主导频率ω=0.035 扰动外，还存在ω=0.071、0.107 和0.141 三种频率的扰动，与GSD 模态M2、M3 和M4 接近，频率相对误差小于3%。这说明凹腔前缘近壁区不稳定性较尾迹区更为复杂，由多种模态主导。

图25 展示了通过前数阶主导GSD 模态对流场快照累计积分重构的结果。可以发现重构流场与原始流场随时间的演化过程曲线整体吻合较好，反映了凹腔流动的GSD 模态能较好地捕捉到大尺度凹腔自激不稳定的动力学特征，可作为原始系统转捩过程研究的低维降阶模型。

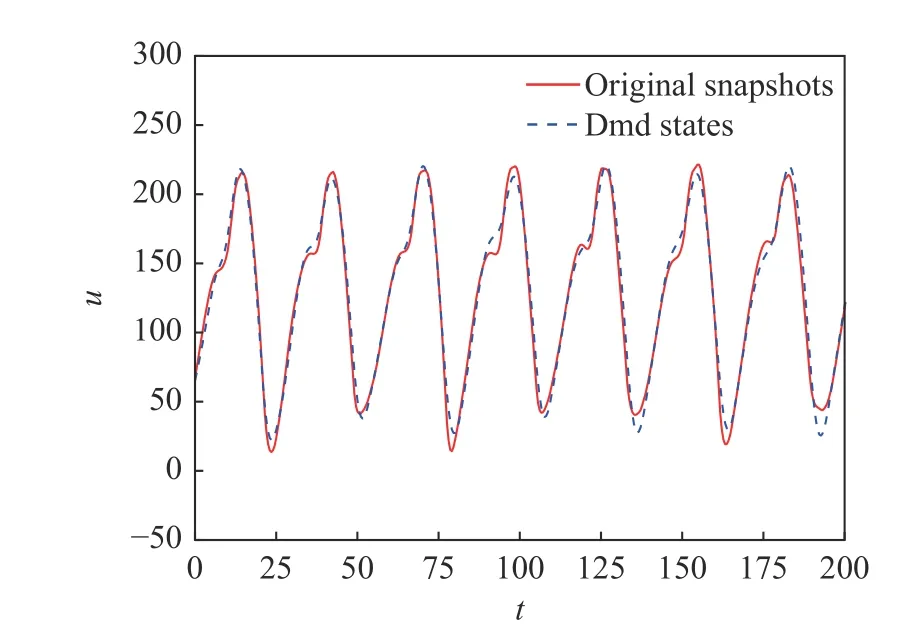
图25 积分重构的速度u 与原始采样信号对比Fig.25 Reconstructed velocity u and the original sampled signal

4 结论

本文针对高超声速和超声速两种典型工况下带凹腔的平板边界层开展了系统的稳定性和扰动演化分析，探讨了不同尺度凹腔对边界层稳定性的影响。研究发现，凹腔内存在多尺度涡结构，且随凹腔尺度的增加其变得愈加复杂。

在高超声速情况下，当凹腔位于同步点上游时会促进扰动发展，位于同步点附近或下游时则起到了抑制作用。当固定凹腔深度、增大宽度时，扰动波抑制效果逐渐增强；当固定凹腔宽度、增加深度时，扰动波抑制效果呈现非单调变化。超声速情况下，凹腔在扰动波不稳定区间内一直起促进效果，当固定凹腔深度、增大宽度时，凹腔对扰动波的促进效果逐渐增强；但当凹腔尺度增加到一定程度，腔体本身自激振荡激发出非定常不稳定波，给凹腔下游边界层引入新的转捩途径，值得后续进一步研究。