高超声速三维边界层转捩数值研究进展及预测软件

黄章峰，张宇琦

(天津大学 机械工程学院，天津 300072)

0 引言

边界层转捩是指边界层流动从层流状态转变为湍流状态的一种自然现象，其物理机理是流动中扰动失稳导致的。对于层流，一般存在流动不稳定特征，因而在外界因素诱导下很容易产生边界层扰动，之后扰动会经历线性和非线性增长，在多扰动相互作用产生的三维涡结构破碎后，流动演变为湍流状态。此时流动中摩擦阻力、热交换、噪声和掺混等相比层流状态均大幅增加，例如湍流热流与摩阻大概是层流的3～5 倍[1]。

在航空航天领域，设计师关心飞行器的气动力热布局，鉴于层流和湍流两种流动状态下热流与摩阻的巨大差别，超声速、高超声速边界层转捩问题已经成为飞行器设计需要考虑的一个关键因素[2]。李志文等[3]从飞行器总体设计角度梳理了高超声速边界层转捩问题研究的必要性和重要性，总结了飞行试验、风洞试验、理论预示等转捩研究手段的国内外研究进展。相比国外，国内在转捩研究领域起步晚了近100 年，在高超声速领域晚了30 多年[4-5]。然而经过40 多年的努力，已经基本与国际先进水平相当。国内转捩研究单位从21 世纪初的以天津大学周恒院士团队为首的几家高校，到2010 年以后覆盖全国高校、研究所，实现了多点开花，特别是2015 年之后，国内在高超声速转捩方面取得了丰硕的研究成果。2016 年，中国空气动力研究与发展中心（简称气动中心）联合天津大学、中国科学院力学所、清华大学、国防科技大学、北京临近空间飞行器系统工程研究所等单位共同承担了科技部“大科学装置前沿研究”重点研发计划中的“高超声速边界层转捩机理、预测及控制方法研究”项目。此后，国家自然科学基金资助的转捩研究项目数也始终保持在两位数（见图1）[6]。

图1 国家自然科学基金支持转捩研究项目历年数量和金额Fig.1 Number and amount of transition research projects supported by NSFC over the years

关于边界层转捩方面的研究进展，国内多名专家已从不同角度作了回顾与介绍[1,7-19]。从这些综述可知，转捩研究对象主要集中在如平板、曲板、后掠翼、零攻角圆锥等二维边界层，在线性增长和弱非线性相互作用两个阶段已获得较全面的认知。然而实际飞行器表面边界层以准三维和三维为主，即流向仍然缓慢变化，但展向流场不再均匀，于是不同的展向区域可能存在截然不同的转捩形态，且扰动呈现三维和展向非周期特征，这给边界层流动稳定性分析和转捩预测造成了巨大困难。随着计算能力的增强和分析手段的丰富，三维边界层的转捩逐渐成为研究的热点之一。本文将对三维边界层转捩机理、转捩预测方法和转捩预测软件等方面的研究进展进行总结，希望为初学者提供有益借鉴。

1 三维边界层转捩机理研究进展

目前研究比较多的三维边界层外形包括后掠翼、三角板、带攻角圆锥、椭圆锥、BOLT（boundary-layer transition）以及气动中心的升力体模型HyTRV（hypersonic transition research vehicle）等。研究结果表明，展向压力梯度驱动的横流、流线汇聚区的流向涡以及流线发散区的接触线是三维边界层中常见的流动形态，与之对应的则是横流不稳定性、流向涡不稳定性以及接触线不稳定性。

1.1 横流不稳定性及转捩

由于压力梯度的影响，边界层内存在一个与外部无黏流相垂直的速度分量，即横流。横流不稳定性属于无黏拐点失稳，扰动通常比黏性不稳定性增长更快，因此在三维边界层中横流失稳机制是主导转捩的机制之一。

牛海波等[20-21]对马赫数6 的后掠平板和三角翼进行了风洞试验，壁面高频压力脉动传感器获得了10 kHz 的非定常横流波信号，并通过基于纳米粒子示踪平面激光散射（nano-tracer based planar laser scattering,NPLS）技术得到了非定常横流涡结构以及其二次失稳结构。赵磊[22]采用改进后的非线性抛物化稳定性方程（nonlinear parabolized stability equations,NPSE）准确预测了后掠平板上定常横流涡的非线性演化过程。Ma 等[23]采用NPSE 和直接数值模拟（direct numerical simulation,DNS）分析了定常横流涡和第二模态的相互作用，并发现一对同频率第二模态扰动相互作用产生定常涡，随着向下游发展逐渐比初始定常横流涡更不稳定。Xu 等[24]采用Floquet 理论对后掠翼定常横流涡进行了二次失稳分析，获得了位于涡顶端的y 模态和位于涡肩部的z 模态，发现了位于涡沟槽部分的新y 模态。新y 模态的增长率大于y 模态，且与z 模态增长率相当。为了进一步探究新y 模态在横流转捩过程中的作用，Chen 等[25]进行了直接数值模拟（DNS），发现高超横流转捩机制与低速情况相似，在二次失稳阶段由z 模态主导。Chen 等[26]研究了高焓边界层横流后掠翼稳定性特征。

后掠板或翼型流场仍存在一个流场均匀的方向，使得采用恰当坐标系可使展向周期条件成立。而有攻角圆锥、椭锥等更复杂的三维外形，流场一般不存在一个展向均匀的方向，稳定性分析更加困难。目前学界在首次失稳方面主要采用一维稳定性分析方法，该方法虽然计算便捷，但需要提前判断扰动传播路径以及展向波数在该路径上的变化[27]。全局稳定性方法可避免上述困难，Paredes 等[28]和Lakebrink 等[29]应用二维特征值稳定性分析方法（BiGlobal）计算了椭锥横流模态，发现其模态形状函数分布在整个横流区。Chen 等[30]运用约化BiGlobal 和面推进抛物化稳定性方法（three-dimensional parabolized stability equations,PSE3D）研究了升力体标模HyTRV 上下表面不同横流区的横流失稳特征，发现每个频率存在数量众多的失稳模态，横流模态最大增长频率在15～30 kHz 之间。Liu 等[31]运用约化方法研究了风洞工况下 6°攻角圆锥横流失稳特征，发现横流全局模态主要集中在背风面，且非定常横流模态比定常模态更不稳定。在横流涡二次失稳研究方面，Moyes 等[32]用NPSE 获得定常横流模态沿特定路径的非线性演化，采用BiGlobal 计算饱和定常横流模态的二次失稳特征。Choudhari 等[33]通过DNS 计算粗糙元阵列引起的横流扰动，并用BiGlobal 和PSE3D 研究横流涡的二次失稳扰动，发现Mack 模态在圆锥侧面横流涡影响下可经历最大可能增长。

1.2 流向涡不稳定性及转捩

早期针对流向涡问题的全局稳定性分析主要集中在HIFiRE-5 模型（2∶1 椭圆锥）的中心线不稳定性上。根据飞行实验，Choudhari 等[34]最先分析了18 km飞行条件下HIFiRE-5 中心线流向涡不稳定性，并发现了一个位于流向涡顶部的不稳定模态。Paredes 等[28]分析了33 km 处的另一个飞行工况，发现主导频率为130 kHz 的对称模态。李晓虎等[35]针对风洞工况进行了研究，分析了不稳定模态的无黏不稳定性特征。Choudhari 等[36]使用PSE3D 对模态在流向上的空间演化进行了分析，发现了PSE3D 和DNS 的结果符合很好。

对于带攻角圆锥的分析则是近年来才开展的。陈曦等[37]基于DNS 扰动时均场，对带攻角小钝锥的背风流向涡进行了全局稳定性分析，根据基本流速度剖面的剪切层位置和模态的相速度，将不稳定模态分为两类，相速度较低的内模态位于近壁剪切层，而相速度较高的外模态位于流向涡顶部的剪切层。BiGlobal 和PSE3D 分析的结果与来自DNS 的转捩数据之间存在一致性，发现外模态不稳定性占主导地位，转捩N值约为10。Li 等[38]研究了相同的模型工况，但使用了无入口扰动的层流场，辨识了Mack 模态，与风洞试验对比得到的转捩N值约为5。Li 等[39]在背风中心线处布置了一个粗糙元，发现外模态增长被显著延后而内模态则被略微促进。Zhang 等[40]研究了5 mm 钝度圆锥飞行工况下的背风面流向涡失稳机理，发现内模态具有声辐射性质，而上游的Mack 模态可在下游转化为剪切模态并可能引起流向涡破碎。

1.3 附着线不稳定性及转捩

附着线附近流场是模型表面边界层在展向最薄的区域，此处扰动失稳频率一般远高于其他展向区域，对实验测量和数值模拟造成巨大困难。Paredes等[28]研究了椭锥附着线失稳特征，发现存在高频Mack模态。Xi 等[41]研究了高超声速来流条件下不同后掠角的后掠圆柱附着线失稳特征，发现大后掠角情形下，在附着线附近呈现典型附着线失稳特征，而在远处则呈现Mack 模态特征。Chen 等[30]同样在升力体肩部附着线区域发现了高频Mack 模态，与前人研究不同的是，此处的附着线流动不再具有展向对称性，原有的对称-反对称模态交替出现的结构坍缩为一支不稳定模态。他们还利用PSE3D 研究了Mack 模态沿下游的演化，发现其扰动局限在附着线附近，从而不太可能与附近横流区的扰动发生相互作用。

圆锥迎风面中心线附近流动也可视为广义的附着线流动。Paredes 等[42]率先对风洞工况下圆锥迎风面失稳开展了全局稳定性分析，发现高频Mack 模态。Chen 等[43]在对飞行工况下的圆锥迎风面开展分析后，同样发现主导不稳定性为Mack 模态，他们进一步将Mack 模态分为D 和S 分支，其中D 模态类似于传统的附着线模态，即呈现对称-反对称模态交替出现结构，且对称模态最不稳定，D 模态集中在迎风中心线附近，而S 模态位于侧面。他们还利用PSE3D研究了不同模态的演化，发现部分S 模态会在下游激发D 模态。杨鹏等[44]对圆锥迎风中心线转捩开展了DNS 研究，证实了Chen 等[43]的结果，即转捩最先在迎风中心线附近发生，且主导失稳模态为Mack 模态。在非线性演化阶段，他们发现了条带结构，推测基频共振是主导非线性机制。

上述转捩机理的研究有助于深刻理解转捩过程，但与准确预测转捩尚有距离。目前主流转捩预测方法是转捩模型和eN方法。

2 三维边界层转捩模型研究进展

转捩模型是基于雷诺平均Navier-Stokes（Reynoldsaveraged Navier-Stokes,RANS）方程的一种模化方法，该方法一般建立在现有成熟的湍流模型基础之上。湍流建模主要是对RANS 方程的雷诺应力项进行封闭，可分为雷诺应力模型和涡黏模型。转捩模型大都是在涡黏模型基础上实现对转捩现象相关统计量的模化，伴随着转捩模式理论的发展不断在推陈出新。在转捩模型的构造与发展中有两个重要概念，分别是间歇因子与非湍流脉动。明晰这两个重要概念的物理意义及其与转捩建模的联系，有助于更深入理解各类转捩建模的物理背景与发展脉络。

间歇因子是对实验观测到的转捩间歇现象的描述。Emmons[45]经过实验发现转捩过程是层流状态下多个孤立湍斑的产生与发展的过程，而非普遍认为的层流流动的简单破碎。基于此，Emmons 提出间歇因子的概念来描述转捩过程，即在转捩过程中转捩区的空间点可以在一段时间内是层流状态、在另一段时间内是湍流状态。间歇因子γ表征了该点在统计意义下的流动状态：γ=0 对应层流，γ=1 对应湍流，而转捩介于两者之间。Dhawan 等[46]给出了间歇因子γ的平板边界层流向分布实验拟合式。因此，间歇因子使转捩模型不再局限于“开关式”的层流/湍流模拟。间歇因子求解主要有代数求解与输运方程求解两种方式。合理的间歇因子求解对于转捩-湍流模型的耦合、转捩区长度的模拟以及三维转捩流场预测具有重要意义。γ-Reθt和k-ω-γ等转捩建模均离不开间歇因子这一重要物理概念。

非湍流脉动的提出同样是基于转捩实验观测现象。在转捩起始位置之前的层流区域，存在不同于湍流脉动的扰动形式，称为层流脉动。Mayle 等[47]提出了非湍流脉动动能这一概念，用以描述上述区域层流脉动的动力学行为。相比前期经验性建模，引入非湍流脉动概念使转捩建模能够引入更多模态信息等转捩物理机制，建立更具有转捩机理可解释性的预测模型，例如k-kL-ε、k-kL-ω、k-ζ、k-ω-γ等转捩模型。

目前见诸文献的转捩模型已不下20 种，其修正改进模型更不胜枚举。本文重点选取了早期的低雷诺数湍流模型以及在学术界、工业界应用研究相对广泛的γ-Reθt模型、k-ω-γ模型和层流动能转捩模型4 类典型转捩模型，就转捩模型构造、模型适用性研究及模型应用情况进行介绍。

2.1 低雷诺数湍流模型

早期的边界层转捩模型预测的尝试，并不是建立相对独立的转捩输运方程，也并未在湍流模型中引入类似间歇因子等转捩相关物理量，而是直接修正低雷诺数湍流模型来预测转捩流动。主要办法是通过对低雷诺数湍流模型中的阻尼函数进行修正，以临界雷诺数为转捩判据，使涡黏系数在临界位置突然增大，造成摩擦系数及边界层厚度增长率“陡升”，从而实现转捩现象的流场模拟。Wilcox[48]通过该办法修正k-ω模型，实现了对槽道、管道湍流以及平板边界层转捩的有效预测。Schmidt[49]在k-ε模型方面亦有关于低雷诺数湍流模型的转捩预测研究。国内严明等[50]基于低雷诺数k-ε模型进行了改进，实现了对T3A 平板边界层的转捩预测。但是相关研究[51]认为，“低雷诺数湍流模型对转捩现象的预测只是一种巧合，其阻尼函数的构造准则是模拟黏性次层，而并未考虑转捩的物理机理”。欧洲于20 世纪90 年代启动的联合研究项目“TransPerturb”对大量低雷诺数湍流模型进行了叶轮机械转捩测试，发现模型存在的普遍问题是预测的转捩位置过于靠前且转捩区的长度过短。虽然该类模型未考虑足够的转捩机理，转捩预测可靠性低，但其构造简单、可实现性强，因此在工程中还是可以基于通用计算流体力学（Computational Fluid Dynamics,CFD）的成熟湍流模型模块进行修正而实现快速应用。

2.2 γ-Reθt 转捩模型

γ-Reθt转捩模型是工程应用最为广泛的转捩模型之一，由Menter 和Langtry 于2004 年[52-53]正式提出，并在2009 年[54]公布了模型的完整构造形式和详细参数设置。该模型的基本思想是在SST 湍流模型[55]的基础上，构造关于间歇因子（γ）和动量厚度雷诺数（Reθt）的两个输运方程。通过求解动量厚度雷诺数，结合风洞实验数据建立的经验关系，来构建用以判断转捩发生的参数，即当地化涡雷诺数与临界动量厚度雷诺数的比值。间歇因子，如前面所述，是对转捩间歇现象的描述，一定程度上可以考虑转捩的物理过程与转捩区的存在。基于间歇因子和动量厚度雷诺数，构建适用于现代CFD 的完全当地化转捩模型。依照该建模思想，基于间歇因子的转捩建模相比于早期的“开关式”的转捩建模，在层流-转捩-湍流耦合计算以及转捩区长度预测方面具有重要的进步意义。采用转捩动量厚度雷诺数输运方程替代传统的非当地变量动量厚度雷诺数来判断转捩发生，便于现代CFD 大规模并行计算，也是γ-Reθt模型的一大特点[56]。

γ-Reθt转捩模型被提出时，还存在很多功能与性能上的不足，需要对模型进行完善与改进以满足工程需求。Langtry 等[57]通过在动量厚度雷诺数输运方程中增加横流项，以流向涡量强度近似判断横流涡强度，完成了模型对横流功能的拓展，实现了模型对三维边界层横流转捩的预测。Menter 等[58]针对伽利略不变性及计算效率低的问题，简化了模型的构造方式，建立了间歇因子单输运方程转捩模型。此外，模型改进还包括外流改进[59]、分离流动修正[60]、与DES 类方法耦合[61]、可压缩修正[62]、横流效应[63]、与神经网络耦合[64]等其他方面。γ-Reθt模型具有完全当地化、可实现性强、易拓展的特点，早期应用于对低速平板、二维翼型、涡轮叶片以及典型三维外形的自然转捩、bypass 转捩、分离诱导转捩及横流转捩的预测。

由于构建γ-Reθt模型所依赖的重要经验关系式是基于低速的风洞试验与数值试验建立的，因此对高超声速转捩的预测偏差较大，需要对模型进行高超声速修正。修正方法主要是对模型中决定转捩位置、转捩区长度的重要经验关系式进行修改或重新定义，使模型具备高超声速转捩预测能力。Krause 等[65]将临界动量厚度雷诺数和调整转捩区长度尺度的函数直接写成来流湍流度的函数，并在双楔外形上得到了验证。张晓东等[66]针对高超声速条件下转捩动量厚度雷诺数显著增大的情况，基于高超声速风洞试验数据，提出了新的转捩动量厚度雷诺数经验关系式，同样在双楔上得到了验证。You 等[67]评估了原始γ-Reθt模型对高超声速边界层转捩的预测性能，并在模型中分别引入Krause 修正、激波探测器以及压力梯度，同时评估了它们的影响，完成了双楔转捩预测的验证。针对后期改进的间歇因子单输运方程转捩模型，Aliaga 等[68]将其成功应用于平板、旋成体等的高超声速转捩预测，但并未论述模型及修正细节。刘清扬等[69]基于γ-Reθt转捩模型，构建了考虑可压缩性的比拟关系（fRe）输运方程，发展了γ-Reθt-fRe转捩模型。陈坚强研究团队通过对γ-Reθt模型展开系统研究，最大程度发挥其优势及潜力。他们基于γ-Reθt模型，提出了稳定性理论、实验和DNS 数据与转捩准则多层级融合的建模思想，形成了涵盖马赫数等参数影响的高超转捩数据集，构造了考虑可压缩、横流、粗糙度等因素的高超转捩准则，建立了C-γ-Reθt高超转捩模型[70-74]，在三维复杂高超飞行器（如升力体标模HyTRV[75]）的转捩预测中取得了非常好的效果（见图2[76]），是目前最有希望应用于复杂工程外形的转捩模型。

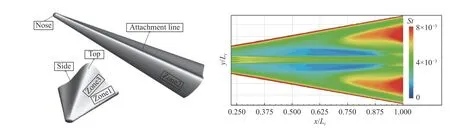
图2 HyTRV 飞行器标模（左）和迎风面转捩模型预测的转捩阵面（右）[76]Fig.2 Aircraft standard model of HyTRIV (left) and transition front predicted by transition modeling at windward (right)[76]

2.3 k-ω-γ 转捩模型

Suzen 等[77]建立了一种比较通用的间歇因子输运方程，方程中包含生成项、耗散项。他们把该间歇因子输运方程与Menter 的k-ω湍流模型相结合，在预测低压涡轮中取得了一定成功。为了便于CFD 计算，需要采用当地变量对模型的失稳模态进行模化。引起转捩的第一模态扰动波和第二模态扰动波等都有不同的特征时间 τnt（或特征尺度lnt）。Warren 等[78-79]基于特征长度构建了层流脉动涡黏系数模型，并采用当地化的参数表示。符松和王亮[80-81]发展了Warren等方法，把模型推广至高超声速转捩情况，命名为kω-γ转捩模型，并引入横流扰动特征时间，使k-ω-γ转捩模型能在名义上体现第一、第二模态及横流失稳的影响，初步实现了高超声速多模态转捩预测（见图3）。

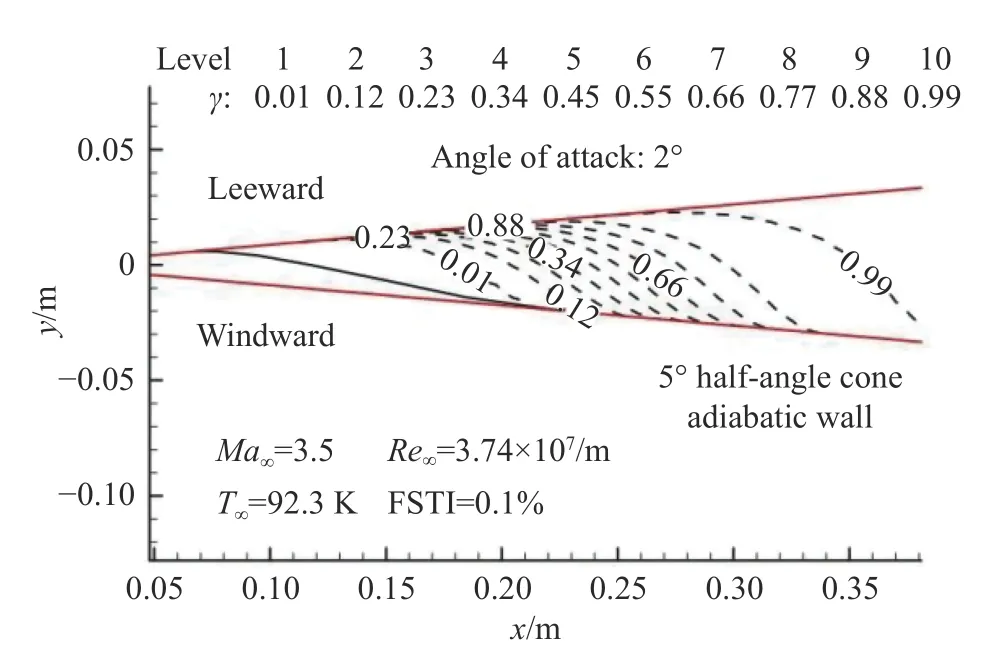
图3 转捩模型预测的高超声速有攻角圆锥转捩阵面[81]Fig.3 Transition front of hypersonic cone with angle of attack predicted by transition modeling[81]

目前关于该模型部署于商业软件的报道尚未见公开文献，但该模型仍在不断发展以提高其工程适用性。郝子辉等[82]采用k-ω-γ模型在高超声速圆锥边界层转捩预测中研究了模型对于头部钝度、来流雷诺数、来流湍流度等的影响规律。Zhou 等[83]对k-ω-γ模型进行了横流拓展，构造了基于横流速度和横流雷诺数的时间尺度项，拓展了模型的高超声速横流转捩预测能力，并应用于高超声速复杂构型[84]。Wang 等[85]对k-ω-γ模型的Mack 模态时间尺度进行了修正，引入了当地化的钝度影响，提升了模型在高超声速圆锥边界层转捩预测中的性能。Zhao 等[86]开展了k-ωγ模型在平板与直锥算例中的参数不确定度量化分析。Yang 等[87-88]将粗糙度放大因子（Ar）输运方程引入模型中，建立了考虑粗糙度影响的k-ω-γ-Ar四方程模型。Zhang 等[89]提出基于流场反演和机器学习的数据驱动框架来提高四方程模型对高超声速边界层转捩的预测能力。刘宏康等[90]初步开展了k-ω-γ模型在高超声速充气式柔性减速器转捩预测的应用研究。

2.4 层流动能转捩模型

层流动能转捩模型一般通过建立层流脉动动能（kL）输运方程，并与湍流模型输运方程耦合求解的方式实现转捩建模与转捩预测。具有代表性的层流动能转捩模型有k-kL-ε和k-kL-ω，用来描述非湍流脉动的动力学行为并预测边界层转捩。

k-kL-ε模型是通过层流脉动动能输运方程与kε湍流模型进行耦合建立的，是首个考虑转捩前扰动增长以及bypass 转捩机制的完全当地化单方程层流动能转捩模型。该模型由Walters 等[91]提出，并部署于商业CFD 软件Fluent 的早期版本中。他们针对边界层转捩之前的层流脉动沿流向增长的特点，基于层流动能一般性动力学特征的假设，建立了“湍流动能-层流动能-耗散率”的三个输运方程，其中层流动能与湍流动能根据壁面距离与湍流长度的一个截断尺度来进行区分，二者之和等于总脉动动能。模型通过对层流动能与湍流动能的建模避免了采用经验公式预测转捩。为提升模型在转捩区的预测能力，Walters 等[92]延续上述思想，进一步在k-ω湍流模型的基础上，完成了k-kL-ω转捩建模，其构造形式与kkL-ε模型基本一致。该模型主要部署在较新版本的Fluent 中。

k-kL-ε和k-kL-ω模型在低速平板、涡轮叶片、机翼翼型的边界层转捩预测中取得了较好的效果，能够较准确模拟反映转捩位置的壁面摩阻分布、热流分布等[91-92]。孙润鹏等[93]将k-kL-ω模型应用于NASAMark II 内冷叶片转捩预测。陈灿平等[94]在k-kL-ω模型中引入了流线曲率因子与间歇因子以改进其对bypass 转捩预测的性能，在DCA 压气机叶珊、S809 翼型、RAE2822 翼型的转捩模型中进行了测试。KOŽÍŠEK 和FÜRST 等[95]在开源CFD 平台OpenFOAM 上实现了k-kL-ω模型，研究了模型在可压缩流动中的表现性能，将模型应用于VKI 和SE-1050 叶栅转捩预测。Salimipour[96]对k-kL-ω模型的分离区模拟性能进行了改进与提升，将模型应用于NACA0012 和Eppler387 翼型的转捩模拟。另外在高超声速领域中，Dash 和Papp 等[97-98]提出的SSGZkLε-γ的层流动能转捩模型及其改进最具有代表性。Shi 等[99]基于高超音速静音风洞实验，提出了一种新的转捩预测工程模型，其预测结果与HIFiRE-5b 的飞行数据非常一致。

3 三维边界层转捩预测eN方法研究进展

转捩预测eN方法通常指基于线性稳定性理论（linear stability theory,LST）[100]的自然转捩预测方法，其理论思想是：边界层内存在各种频率扰动向下游演化增长；针对层流场通过求解某种简化形式的线性稳定性方程获得扰动增长率，然后沿扰动波传播方向积分增长率获得扰动幅值的指数增长倍数N值（又称放大因子），最后判断包络的N值是否达到临界的Ntr来确定转捩发生位置；Ntr的值可通过转捩实验标定获取。不过eN方法仅仅考虑了转捩的线性稳定性阶段，未考虑转捩的感受性和非线性失稳阶段，所以Ntr值的判据标准受限于对感受性与非线性失稳的认识。因而，eN方法实际上是一个半理论半经验的方法。尽管如此，对于小幅值的环境扰动或来流扰动诱导的边界层自然转捩，因为扰动线性失稳一般占据大部分区域，还因为感受性阶段和非线性阶段的贡献可以在N值标定中间接体现，所以eN方法是比较可靠的转捩预测方法。例如高超声速巡航飞行器，高空大气环境扰动通常为小扰动，飞行器表面的转捩现象一般为自然转捩过程，满足eN方法使用条件。

eN方法早在1956 年[101-102]就已经被提出来，对于飞行器大面积处边界层三维性较弱时，eN方法能够有效地预测转捩位置。但对于具有复杂外形的三维边界层，距离工程应用还有很大距离[103]。如何面向复杂多块化、结构与非结构化网格数据、有效识别转捩模态、在三维空间上模态积分等是eN方法工程应用面临的重要技术难题。

采用平行流假设和展向均匀假设的LST 是常用的理论分析方法。对于横流区和附着线区流动，由于流动在展向变化较缓，LST 能定性甚至定量准确地捕捉扰动波的某些重要信息（如频率、增长率和相速度等），但对于流向涡区，流动在展向剧烈变化（展向梯度幅值与法向梯度幅值相当），此时LST 已不能准确预测流场失稳行为，而考虑展向和法向流场变化的全局稳定性分析方法，则可准确获得上述三维流场的稳定性特征[104]。

根据流动三维特征的复杂程度，全局稳定性分析方法主要可以分为三类：流向基本不变、法向和展向快变的BiGlobal，流向缓变、法向和展向快变的PSE3D，流向、法向和展向均快变的三维特征值稳定性分析方法（TriGlobal），下面分别介绍其基本思想。

3.1 二维特征值稳定性分析方法（BiGlobal）

在开展全局稳定性分析前，需要将不规则的物理域变换到规则的计算域下。通常采取的坐标变换形式为 (x,y,z)→(ξ,η,ζ)，其中 (ξ,η,ζ)∈[-1,1]，该坐标系的选取使得边界层流场沿 ξ方向缓变，于是若采用平行流假设，则有如下分解：

其中q=(u,v,w,p,T)，u、v和w分别为流向、法向和展向速度，p为压强，T为温度。t为时间，代表时均场，为扰动形状函数，ω为扰动频率，α为待求的扰动波数（实部）和增长率（虚部），c.c.代表共轭。将上式代入Navier-Stokes方程，保留一阶小量，可得空间二维特征值（BiGlobal）方程：

其中A0、A1、A2是包含时均场信息的算子，可采用高阶有限差分离散，法向和展向根据计算域和不稳定性性质的不同分别采用数目不等的网格数。法向和展向一般选用齐次边界条件，在对称面处采用对称或反对称条件。式（2）的特征值采用隐式Arnoldi 迭代求解。

3.2 面推进抛物化稳定性方程（PSE3D）

为考虑非平行效应的影响，将流场作如下分解：

其中，假设时均场和扰动形状函数均沿流向缓变，则在仅保留其一阶流向导数项后，可得面推进抛物化稳定性方程（PSE3D）：

其中 L 和 M为包含时均流场信息的微分算子，离散方式与BiGlobal 方程一致，初始条件由BiGlobal 给出，流向推进一般采用一阶或二阶隐式欧拉格式，为保证形状函数沿流向缓变，需在每步迭代α使得

其中ME代表能量权矩阵，通常采用如下形式：

其中，γ为比热比，T为温度，ρ为密度。不同的能量权矩阵对结果有一定影响。

上述方法在研究流向涡与接触线等具有展向局域分布的不稳定性时具有较高效率，但在面对展向分布区域广而展向波动剧烈的横流不稳定性时则需要很多展向网格点，内存消耗大，计算时间长。为此，Chen 等[30]提出约化方法，利用横流全局模态具有慢变的幅值和快变的相位的特点，将横流特征函数作如下分解：

此时，通过试错法或者迭代法选取合适的等效波数 β，使得：

即形状函数在展向的波动主要吸收进指数项 exp(iβζ)。将式（7）代入式（2），并消去指数项，可得约化全局稳定性方程：

3.3 三维特征值稳定性分析方法（TriGlobal）

当流场在三个维度都非缓变时（如三维凹腔、粗糙元等），流场不稳定性需求解三维特征值问题，即TriGlobal。TriGlobal 问题矩阵规模巨大，显式写出系数矩阵并求解该矩阵特征值这一常规方法几乎不可行。为此，Tu 等[105]提出基于隐矩阵投影的无矩阵全局稳定性分解方法，为解决强三维稳定性分析问题提供可行的思路。该方法的思想是通过反复调用CFD 求解器构造原特征矩阵A（m×m维）的子空间S（n×n维，n≪m）实现降维处理，进而找到工程上最关心的数个主特征值。具体思路如下：

首先选择一系列线性无关的初始扰动：

通过高精度的CFD 工具，让扰动场演化 ∆t时间后得到，

其中矩阵B=exp(A∆t)。可以投影处理构造小矩阵

其中Q、R对应Um的QR 分解矩阵，满足Um=QR，且可以证明矩阵S与矩阵A的特征值 ω和特征向量 φ满足以下关系，

Tu 等[105]的方法通过CFD 求解和子空间投影，避免了构造巨型矩阵A，把全局稳定性理论的巨型矩阵特征值问题转化成小矩阵特征值问题，对于高雷诺数流动，矩阵降维可达4 个量级以上，使三维复杂飞行器的转捩机理分析变得可能。

除上述方法外，基于数据驱动的动态模态分解（dynamic mode decomposition,DMD）方法（及其变种）也是常用的全局稳定性分析方法[106]。

4 三维边界层转捩预测软件研究进展

鉴于eN方法的理论优势与精准效果，21 世纪以来，国内外陆续攻克了eN方法的相关技术问题，并汇编成转捩预测软件，使其在工程实践中得到了广泛应用。下面介绍几款基于eN方法开发的典型转捩预测软件。

4.1 eMalik 软件

eMalik 是由NASA 下属机构兰利研究中心（LaRC）的Malik 主持完成的一款二维稳定性分析软件，并于1991 年底交付给美国空天飞机（NASP）项目组使用，取得了良好的效果。在意识到该软件对支撑高超声速飞行器设计的重要性后，又将该软件与CFL3D对接，实现层流场计算与转捩分析的功能集成。1992 年底，Malik 还将三维稳定性分析代码的预发布版本交付给项目组。eMalik 软件的主要功能是预测典型外形边界层的转捩模态，包括第一模态（TS 波）、第二模态、横流模态、Görtler 失稳模态等。

eMalik 软件的产品具体信息并未在互联网上公开，文献提到的两份关于eMalik 软件的报告（No.88-6和No.HTC-8902）国内也没有相关获取渠道。不过，追溯Malik 早期发表的关于eN方法代码的文章，可以发现，名为COSAL[107]的软件可能与eMalik 软件存在关联。COSAL 软件是最早开发的用于可压缩边界层转捩预测的封装代码之一，然而并没有集成到任何CFD 求解软件上。它需要提供外部层流场，手动输入所需的波参数，N值积分方法使用局限，对使用人员专业水平要求高，因而没有得到工程上的广泛应用。后来以NASP 计划为契机，发展了更为实用的eMalik软件。还进一步发展了集成流场计算、稳定性分析和转捩预测功能的一系列软件工具包（graphical transition prediction toolkit,GTPT）[108]。

eMalik 软件在美国几家具有军工背景的单位中得到了使用。从几篇公开的文献可以看出，eMalik 软件应用的外形偏简单，但仍对飞行器发展、风洞喷管设计等起到了支撑作用[109]。美国麦克唐纳·道格拉斯公司（McDonnell-Douglas Corporation）Elias 等[110]针对NASP 几何外形测试了eMalik 软件，成功预测了高超声速边界层转捩。普渡大学Schneider[111]利用eMalik 软件分析了风洞喷管的Görtler 失稳对喷管内表面转捩的影响，有效评估了设计喷管对要求获得低噪声层流化喷流的达标情况。美国空军基地Kimmel 等[112]针对椭圆锥模型利用eMalik 软件预测了横流转捩特征，该模型后来成为了飞行试验HIFiRE-5 的基准外形[113]，也就是美国空军基地联合澳大利亚国防科技组织发起的高超声速飞行试验计划[114-115]的系列之五，目的是验证美国新一代高超声速飞行器发展的关键技术。但是，eMalik 软件作为设计工具的功能还是很有限，其主要原因是不能分析复杂外形的流动稳定性与转捩特征，软件运行需要大量的人工干预，而且在当时的计算条件下完成分析需要的时间比较长。也许是基于这些原因或局限，后来少有文章对该软件进行更新报道。

4.2 LASTRAC 软件

LASTRAC（Langley stability and transition analysis code）软件是由美国NASA 兰利研究中心Chang[116]于21 世纪初完成的一套功能强大的转捩预测软件。虽然它与eMalik 软件同属一家单位，开发时间晚于后者十几年，但与eMalik 软件并不是前后传承关系。LASTRAC 软件是从零开始开发的，基于面向对象进行设计与编程，以便于后期维护与扩展。LASTRAC软件在功能上得到了很大拓展，它不仅包含基于LST 的传统eN方法，还包含考虑非平行效应的线性和非线性抛物化稳定性分析方法（PSE）。这样一方面可以采用传统的基于LST 的eN方法来分析边界层线性稳定性与转捩预测，还可以采用更为高级的基于PSE 的eN方法；另一方面可以利用线性和非线性PSE 模拟边界层的转捩过程，相较于直接数值模拟和大涡模拟，大幅降低计算时长。

从适用外形上看，LASTRAC 软件主要有两个版本，分别是2D 版[116]和3D 版[117]，于2003 年和2004 年公布。2D 版适用于二维边界层、旋转体边界层、无限后掠机翼边界层、二维射流、轴对称喷流和涡流等。3D 版进一步引入了三维PSE 方法，将适用范围拓展到准三维或一般三维边界层，如有限后掠翼、锥体、有攻角模型等。LASTRAC 软件基本上为航空航天飞行器的所有典型边界层的转捩预测与层流控制研究提供了可靠的工程实用工具。2018 年Kline 等[118]进一步考虑了高温化学反应效应。2023 年，LASTRAC软件被集成到了著名的流动仿真软件OVERFLOW，实现了流动仿真与转捩预测同时进行[119]。此外，LASTRAC 软件的用户界面设计可以减少用户在识别扰动不稳定频率和波数方面的人工干预，提高软件对用户的友好性。

LASTRAC 软件一问世就在美国军工和高校单位推广起来。NASA 兰利研究中心的转捩研究团队（由著名转捩学者Chang、Choudhari、Li Fei、Paredes 等组成）依靠该软件分析了飞行试验HIFiRE-1（零攻角和有攻角圆锥外形）和HIFiRE-5（椭圆锥外形）的转捩机理[28,34,120-121]。该团队还对美国的火星科学实验（mars science laboratory,MSL）再入飞行器的转捩进行了分析，有效评估了热载荷分布对精确着陆所需升阻比的影响情况[122]。此外，该团队还联合美国航空航天研究所将LASTRAC软件与著名非结构有限体积RANS 求解器FUN3D 软件进行耦合，发展了用于转捩分析的基本流剖面提取技术，建立了转捩预测模型，预测了G-3 整机飞行器的N值分布，有效模拟了NLF(1)-0416 翼型和6∶1 标准椭球体转捩前后的热流摩阻变化（见图4）[123-124]。美国霍普金斯大学应用物理实验室利用该软件分析了BOLT 外形的转捩模态失稳机理，支撑了试验外形的设计与优化以及飞行验证试验[125]。该试验是由美国空军研究实验室（AFOSR）牵头的，主要用于研究具有后掠前缘的凹曲面三维边界层转捩问题（见图5）[126-127]。美国波音公司利用该软件对美国圣母大学马赫数6 静音风洞喷管进行模态分析，有效支撑了优化喷嘴外形和壁温分布的设计[128]。

图4 LASTRAC 和FUN3D 耦合计算得到的G-3 飞行器转捩摩阻等值线[124]Fig.4 Transition friction contours of G-3 aircraft obtained by coupling LASTRAC and FUN3D[124]

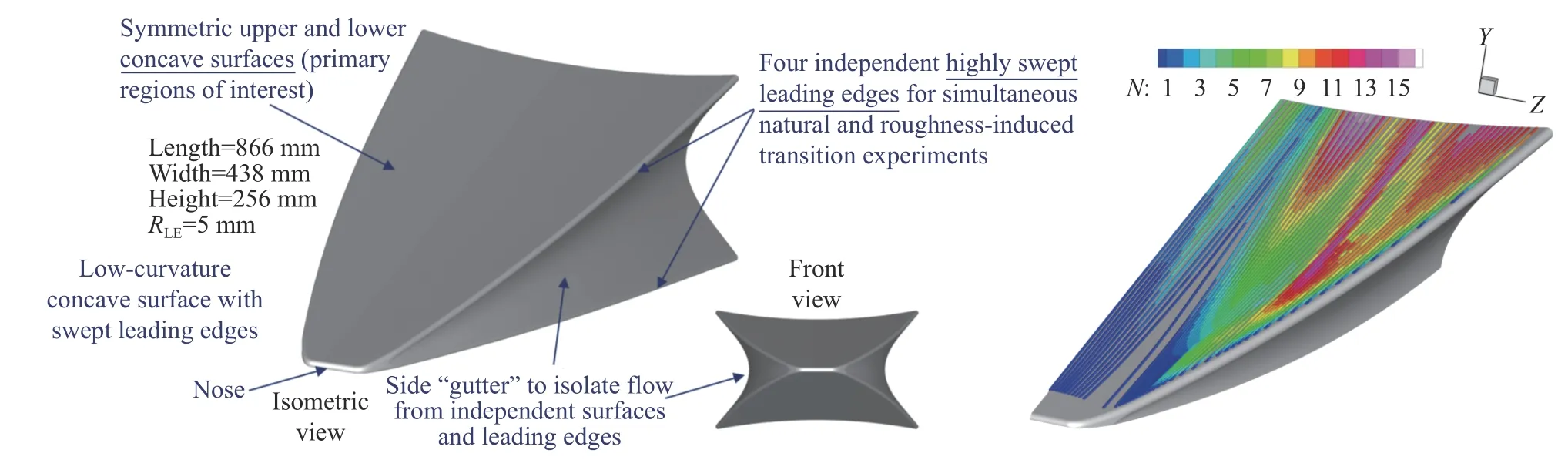
图5 BOLT 飞行器标模（左）和LASTRAC 预测的转捩阵面（右）[126]Fig.5 Aircraft standard model of BOLT (left) and transition front predicted by LASTRAC (right)[126]

4.3 LILO 软件

LILO 软件是德国宇航中心（DLR）针对航空飞机转捩问题而设计的一款工业分析软件。该软件于2004 年9 月首次公开了使用说明书，2006 年7 月又发布了2.1 版[129]。它是基于Fortran 77 语言开发的，可分析考虑表面曲率的不可压/可压缩准三维边界层的转捩预测问题。从适用范围上来说，LILO 软件相比前面介绍的两款美国软件，通用性较弱，在高速航天领域的应用方面更是未见到相关报道。它的优势在于应用了数据库方法，包括特征值数据库和转捩N值数据库，与RANS 流场求解器进行耦合，且在计算过程中与流场求解器交互，实现了软件的高效计算和自动预测功能。特征值数据库是以神经网络形式表示，可以基于基本流剖面（如Falkner-Skan-Cooke 剖面）通过机器学习训练获得[130]。该数据库用于寻找初始模态值，有助于计算快速收敛到正确解。转捩N值数据库是通过大量实验标定建立的转捩判据。当计算的N值曲线达到转捩N值数据库中的临界值时，即可判断转捩发生。该数据库可以将eN方法以全自动的方式应用于转捩预测，并且在基本无需提前认识转捩特征、无需用户干预的情况下，完成转捩位置的迭代分析[131]。

LILO 软件主要用于指导机翼、机身、短舱、尾翼等航空飞机部件的自然层流（natural laminar flow,NLF）设计和混合层流控制（hybrid laminar flow control,HLFC）设计，是一款专用性很强的转捩预测软件。它一般不单独使用，而是集成到一些流场模拟软件上，实现转捩预测分析与转捩场模拟的同步计算。例如，DLR 将LILO 软件集成到自身开发的两款三维RANS求解器FLOWer[130-131]和TAU[132]上，主要服务于欧洲空客公司。

FLOWer 是一个基于有限体积法开发的三维可压缩RANS 软件，适用于多块结构化网格，可求解定常或非定常流场问题。当转捩预测模块耦合到FLOWer求解器时，耦合系统成为一个有效预测转捩位置、快速模拟从层流到湍流的转捩流场的CFD 工具，在已知模态（T-S 波和横流模态）转捩判据的情况下，全程自动化运行，基本无需用户干预。该套耦合系统的实用性在ONERA 设计的M6 机翼[133]上得到了检验。

TAU 是由DLR 于20 个世纪末开发完成的一款非结构/混合网格三维RANS 求解器。该求解器可实现高精度层流边界层流动剖面的计算或提取，更适用于边界层转捩预测分析。布伦瑞克大学流体力学研究所（ISM）在TAU 软件中引入耦合了LILO 转捩预测模块，实现了对三维边界层转捩的快速自动化预测功能[134]。后来两家单位不断合作，将TAU 软件的转捩预测功能进一步优化，对标应用于工业飞机中机翼、尾翼、机身和短舱等复杂配置[135-139]，如荷兰航空航天实验室设计的二段NLR-7301 翼型（图6 左）[136]、DLR 设计的DLR-F11 翼身组合体（图6 右）[136]、NASA的CRM-NLF 机翼（图7）[139]。

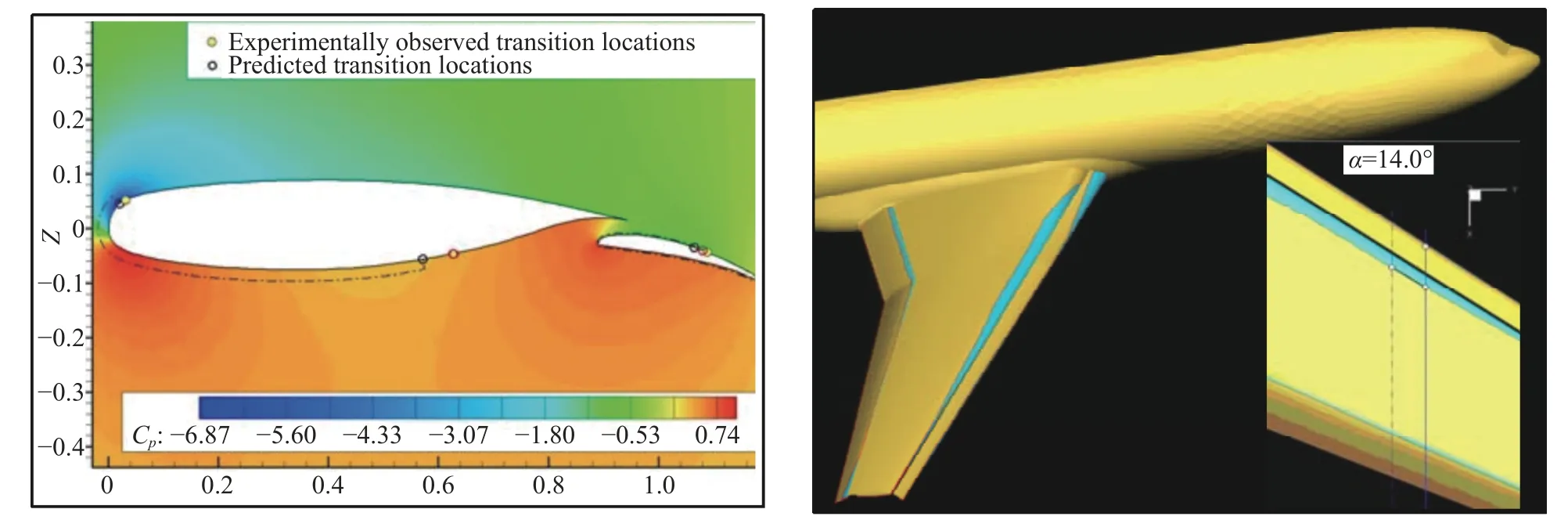
图6 LILO 预测的NLR-7 301 翼型（左）和DLR-F11 翼身组合体（右）的转捩结果[136]Fig.6 Transition result of NLR-7 301 Airfoil (left) and DLR-F11 wing-body (right) predicted by LILO[136]

图7 LILO 预测的CRM-NLF 翼型转捩阵面[139]Fig.7 Transition front of CRM-NLF Airfoil predicted by LILO[139]

4.4 HyTEN 软件

HyTEN 软件[140]是一款用于高超声速边界层稳定性分析与转捩预测的软件，由气动中心联合天津大学在国家数值风洞NNW[141]（National Numerical Windtunnel,NNW）工程资助下开发的。该软件最早是由天津大学汇编集成LST 代码和转捩预测代码，经过多个版本迭代更新，成功实现从二维、准三维外形到三维外形的应用[142-146]。其中较为典型的是天津大学黄章峰[147]发展的流动稳定性分析和转捩预测（flow instability and transition,FIT）软件，该软件实现了飞行器大面积处转捩的自动、高效、准确预测，且在工程单位得到了应用。后来以NNW 为契机，气动中心联合天津大学，瞄准工程化、实用化需求，在原来基础上增加了全局稳定性分析模块、感受性模块和天地转捩数据模块等，提升了代码的适用性，并对转捩预测代码进行优化、测试、集成，形成了HyTEN 软件。此外，HyTEN 软件也在国内多个飞行器设计部门得到了应用，并取得了良好效果。

HyTEN 软件是基于面向对象思想设计的，软件核心部分采用Fortran 语言编写，继承了Fortran 语言计算效率高的特点，同时兼顾软件的代码维护、功能扩展和数据对接等。HyTEN 相较于美国eMalik 和LASTRAC，优势包括理论更完备（如全局稳定性理论），通用性更强，适用更复杂三维外形，灵活匹配多块结构和非结构网格流场等。HyTEN 还能自动识别和处理给定的网格和流场，不需要输入其他网格信息、边界信息、流场信息等，然后利用插值技术自动提取边界层流场剖面信息，从而自动完成流动稳定性与转捩预测的前处理准备工作，整个过程无需人工干预。因此，该软件可以作为独立软件分析不同CFD 求解器计算的流场数据，适合在行业内推广应用。软件采用了OpenMP 并行，大大提高计算效率；可调用感受性数据库，提供N值积分初始幅值，提高转捩预测准度；可调用转捩的数据库，加快计算收敛速度，实现转捩高效预测。另外，除了一维线性稳定性理论，软件还可以选用全局稳定性理论，实现一般三维边界层的流动稳定性分析与转捩预测。

HyTEN 软件因其通用性和友好性，被广泛应用。目前公开的有：Wan 等[148]分析了有攻角飞行试验的转捩问题，证实了飞行试验中测量的5～20 kHz 低频信号为横流行波，首次澄清了困扰学界多年的关于定常-非定常横流模态主导性的争议；涂国华等[149-150]将风洞试验与飞行试验数据进行关联，建立了风洞试验转捩数据关联方法和转捩天地相关性，为工程上飞行转捩预测提供了有效方法；陈坚强等[151]分析了HyTRV 流场特征与边界层稳定性特征；对于复杂三维外形，黄章峰等[12]对HIFiRE-5 椭圆锥（图8 左）、Xiang 等[76]对HyTRV 升力体（图8 右）的转捩预测结果（线条）与实验结果（背景颜色）对比都有非常好的吻合度。

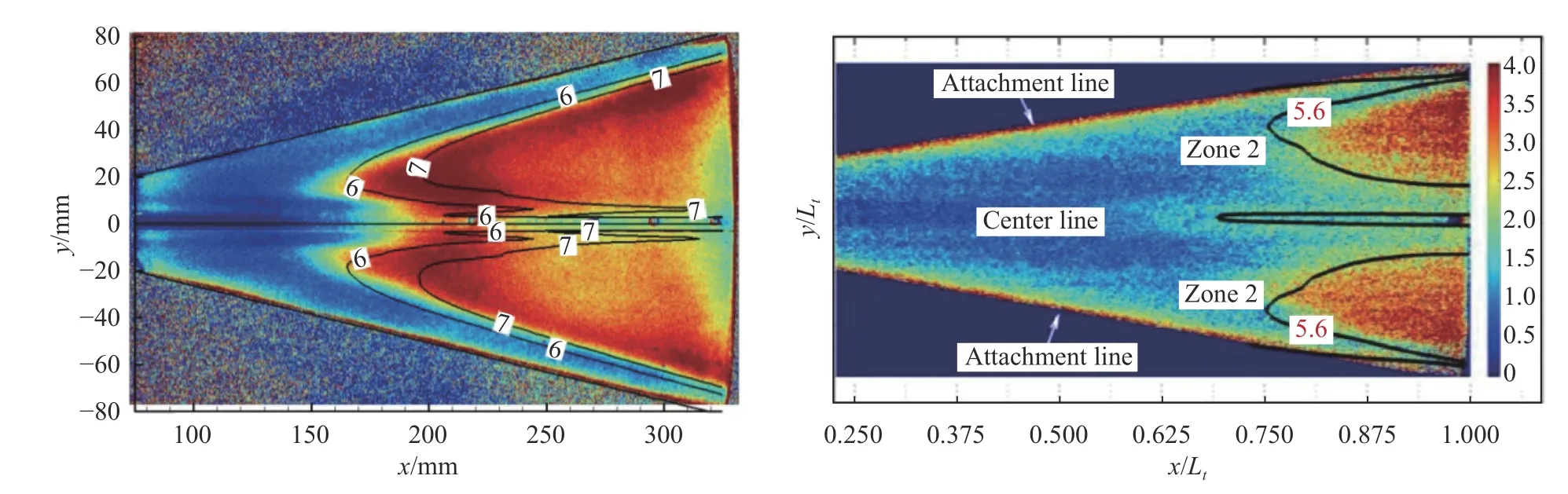
图8 HyTEN 预测的HIFiRE-5（左）[12] 和HyTRV（右）[76]的转捩阵面Fig.8 Transition front of HIFiRE-5 (left)[12] and HyTRV (right)[76] predicted by HyTEN

4.5 其他转捩软件

以上介绍了4 款典型软件，但基于eN方法的转捩预测软件不止于此，且在工程应用与科学研究中都发挥了重要作用。例如，美国明尼苏达大学受美国空军研究实验室赞助开发了一款转捩分析软件（STABL）[152]，早于LASTRAC 软件考虑了高温热化学平衡或非平衡效应，主要用于解决高马赫数飞行器的转捩问题，如HTV-2 飞行器、X-51 飞行器、Reentry-F 再入飞行器等。进一步地，他们将STABL 软件耦合到他们新发展的非结构网格求解器US3D 软件[153]，可用于分析飞行器表面烧蚀等物理现象。该软件已经在美国空军、NASA、桑迪亚实验室、各大飞机制造商和高校等推广应用[154]。

此外，美国得克萨斯州农工大学基于PSE 方法开发了EPIC 软件[155]，可解决有攻角圆锥、裙锥、HIFiRE-5 椭圆锥等三维边界层的线性和非线性稳定性问题。ONERA 的Arnal 等[156]根据自相似流动特征，通过稳定性分析形成数据集或关系式，建立了转捩预测的数据库方法。他们前后工作三十多年完成了数据库方法从二维到三维边界层甚至复杂构型的应用发展，可以说是该方面工作的集成者。前面提到的LILO 与FLOWer 耦合系统、LILO 与TAU 耦合系统引入的数据库方法都是基于该成果发展的。后来他们将数据库方法耦合到ONERA 开发的elsA 软件中，并在空客A310 翼型上得到了检验与应用[157]。瑞典国防研究局将转捩数据库方法耦合到自主开发的FOI-Edge 求解器，成功应用于美国HiLiftPW-1 中的大弦三段梯形翼型的转捩预测[158]。俄罗斯的Boiko 等将eN转捩预测模块耦合集成到LOGOS 软件上，形成转捩的自动分析软件LOTRAN[159-160]，在机翼、长椭球体和发动机短舱成功应用。

在国内，西北工业大学将eN方法耦合到三维RANS 求解器PMNS3D，实现对DLR-F4 翼型[161-162]、空客A320 翼型[163-164]、自然层流机翼[165]、翼型优化[166]的转捩自动预测。中国航空工业空气动力研究院将eN方法先后耦合到UNSMB[167]和AIR_OVERSET[168]数值模拟平台上，并采用法国航空航天研究中心ONERA-M6 翼型、麦道航空公司30P30N 三段翼型和德国宇航中心DLR-F4 翼型等算例进行了验证。

5 结论与展望

高超声速边界层转捩预测是飞行器热防护设计与减阻增升设计需要考虑的重要问题，本文主要针对三维边界层的转捩机理、转捩模型、预测方法、预测软件等四方面研究现状进行了梳理与讨论，主要结论与认识如下：

1）相比二维边界层，三维边界层呈现三类特有的流动结构，即横流、流向涡和附着线流动，每类结构具有不同的失稳特征和转捩机理，需要分别加以深入研究。目前，三维边界层的线性失稳模态特征已逐渐清晰，但非模态扰动演化和模态非线性相互作用机制还不清楚，非线性转捩机制的研究近乎空白，亟待后续大量持续的工作。

2）转捩模型的主要实现方式是通过在湍流模型输运方程基础上，耦合求解转捩模型输运方程与湍流模型输运方程来实现的。伴随转捩模式理论的发展，转捩模型处于不断发展与改进的过程之中。本文主要介绍了低雷诺数湍流、γ-Reθt、k-ω-γ、层流动能4 种常用转捩模型的构造、适用性及应用情况。目前在商业软件上部署的转捩模型数量相对较少，主要是γ-Reθt转捩模型及其改进模型。转捩模型应用范围包括内外流条件下各类外形的二维、三维的自然转捩、旁路转捩、分离诱导转捩，速度域涵盖从低速到高超声速。但由于转捩机制的复杂性，单一转捩模型在面对来流条件和几何外形的巨大差异时难以表现出一致的普适性。这对未来发展具有通用、普适、可靠的转捩模型提出了更高要求。

3）eN方法是基于流动稳定性理论的自然转捩预测方法，是目前理论依据相对充分的一种半理论半经验方法。尽管该方法的理论基础相当成熟，但如何将科学方法上升到实用的工程技术是国内外一直不断攻关的技术问题。本文梳理了基于eN方法的转捩预测软件的开发与工程应用情况，重点介绍了eMalik、LASTRAC、LILO、HyTEN 四款典型转捩软件的优缺点。国内软件的发展相比欧美较晚，但经过十几年的努力实现局部赶超，并且开始推广到相关工业部门。

基于eN方法的转捩预测软件可实现对航空航天飞行器的横流、流向涡、附着流等典型三维边界层的自然转捩预测，特别是在高超声速领域取得了理论与技术上的突破，包括实现三维边界层转捩预测、耦合高温气体效应、转捩的自动化预测等，深受国防工业部门的青睐。但是，面对多模态转捩现象，仍缺乏统一的转捩判据，需要加强转捩判据数据库的建设。