带冰翼型失速分离流动数值模拟和模态分析

2024-01-09杜孟华田琳琳朱春玲

空气动力学学报 2023年11期

杜孟华，田琳琳，朱春玲

(南京航空航天大学航空学院，南京 210016)

0 引言

飞机在起飞或降落过程中，会遭遇过冷云层，过冷云层中的过冷水滴撞向飞机表面产生积冰，而机翼结冰后其前缘形状被破坏，气动特性发生改变，对航空安全造成严重威胁。其中，角状积冰对飞机飞行安全的影响最大。角状积冰后的流场结构比较复杂，旋涡相互作用，冰角后方脱出的自由剪切层出现失稳[1]，非定常效应占主导地位[2]。另一方面，对带冰机翼流动分离的预测和分析，直接影响气动力和飞机操纵稳定性分析，进一步影响飞机在结冰状态下的安全性评估。因此对带冰机翼进行数值模拟和气动分析成为研究热点和难点。

计算流体力学（CFD）方法是研究带冰翼型气动特性的有力工具。早期研究中，使用雷诺平均（Reynolds averaged Navier-Stokes,RANS）方法进行数值模拟，但此方法采用时均化处理，难以捕捉到带冰翼型的精细化流场结构[3]。而后，为了提高结冰引起的流动分离预测精度，张恒等[4]使用改进延迟脱体涡（improve delayed detached-eddy simulation,IDDES）方法对带冰翼型进行模拟，结果表明IDDES 方法有效解析了分离区小尺度的湍流结构，且较为准确地预测了大尺度分离泡的再附位置。Hu 等[5]采用IDDES 方法对脊冰和角冰进行了数值模拟，成功捕捉到多尺度涡及相关流动结构。为进一步精细化研究带冰翼型问题，清华大学Xiao 等[6]通过IDDES方法结合涡度相关的亚格子长度尺度和剪切层的亚格子长度尺度，对角冰问题进行研究，新的长度尺度准确地捕捉到初始自由剪切层涡的卷曲和配对模式，同时正确地预测了再附区涡脱落的频率。Xiao 等在另一项研究中[7]采用壁模型大涡模拟对三段翼结冰流动分离进行了模拟研究，捕捉其非定常流动特性。

在非定常复杂流场研究中，构建流场的降阶模型可得到复杂流动现象的主要特征，有助于进一步分析其流动机理。基于流场特征提取，主要存在两种典型的降阶模型：本征正交分解（proper orthogonal decomposition,POD）[8]方法和动态模态分解（dynamic mode decomposition,DMD）[9]方法。

前人采用这两种模态分解方法对机翼绕流后的流场进行了一系列的分析研究。例如，Ohmichi 等[10]采用DMD 方法对三维后掠翼跨声速抖振的主要流动结构和非定常特性进行了研究。Ricciardi 等[11]采用不同的正交分解技术研究了NACA 0012 翼型中的湍流相干结构，主要使用了滤波POD 和频域POD 描述相干结构的动力学特征，并将它们与噪声联系起来。国内，王晋军团队[12]使用DMD 方法对实验中NACA 0015翼型加装Gurney 襟翼后的尾流速度场进行了分析。叶正寅团队[13]应用DMD 方法提取了NACA 0012 翼型在大迎角流动中的主频和高频倍率及对应的流场模态结构。张伟伟团队[14]对机翼跨声速抖振进行数值模拟和模态分析，通过DMD 方法研究了激波展向失稳特性，结果显示机翼的展长和后掠是主要的诱因。张辰等[15-16]使用POD 方法对NACA 23012 带脊冰的模型提取特征模态，研究脊冰后的三维湍流尾迹流动特征。综上，采用模态分析对机翼绕流作研究，主要围绕尾迹结构[17]、几何形状[18]、翼尖涡[19]、气动声学[20]和抖振[21]等方面，而利用模态分析方法开展结冰问题稳定性分析的研究较少。

在对非定常流场进行模态分解后，往往会使用分解后的模态对流场进行重构，用较少的模态即可对流场还原，达到数据压缩的效果。对于流场重构，Rajmohan 等[22]采用POD 方法对舰面非定常流场进行重构，以解决舰面流场数据量过大的问题。Zhan 等[23]基于POD 方法和机器学习方法构建降阶模型以快速重构飞机结冰现象、支持飞机结冰的适航认定，从而提高航空安全。Sun 等[24]通过POD 方法建立了一套风场快速重构的方法，可以提供精确的空间分布律，以克服传统计算方法计算量大的问题。

从前述可知，一方面，当前针对翼型结冰问题的研究较少，且大多数的研究都集中在结冰后的稳态影响上，不能描述结冰后的不稳定性；另一方面，采用模态分析对带冰翼型流场分析的研究更少，特别是对角状积冰的研究。前人有关结冰研究的结果表明，分离泡的发展和诱导稳定性是理解角冰流场的关键；模态分析方法对分析主要模态和运动频率存在优势。同时，当前航空领域对飞机防除冰问题精细化模拟和对带冰机翼的全局稳定性分析有着迫切需求。因此有必要对带冰机翼开展数值模拟和模态分析研究。

本文采用IDDES 方法开展带角状积冰翼型绕流非定常模拟研究。在此基础上分别采用POD 和DMD方法对非定常流场数据进行模态分解，分析带冰翼型在近失速条件下的流动变化特征。此外，在多步长结冰数值模拟中，因角状积冰而产生的非定常流场数据量大，计算效率低。因此对某一时刻的流场分别进行POD 和DMD 重构，以验证两种方法对流场特征提取的效果，同时也为在结冰模拟过程中使用模态分析方法进行流场重构数据压缩提供参考。

1 计算方法

1.1 非定常流场求解方法

考虑控制体流体微团Ω，三维积分形式的N-S 方程可以表达如下：

其中：Ω为控制体，W为守恒变量，Fc和Fυ分别为对流矢通量和黏性矢通量。

使用有限体积法对方程进行离散。其中，对流通量采用HLLC 格式，时间推进采用隐式LU-SGS 方法，求解非定常流场采用双时间步推进。选用基于SSTk-ω两方程模型的IDDES 方法需要构造新的湍流混合长度，具体公式如下：

式中，fhyb为混合函数，fres为升降函数，lRANS为RANS 的长度尺度，CDES为亚格子模型常数，Δ为亚格子尺度，定义如下：

式中，Cw为经验常数，dw为网格单元到壁面的距离，hmax为三个方向上网格最大步长，hw,n为壁面法向网格单元尺度。

1.2 POD 方法简介

POD 方法是一种模态分解技术，它本质上是将流场分解为若干正交基，选择流动的主要模态对流场进行近似描述。POD 给出具有最小基向量的正交集，在构建流场降阶模型时非常有用。POD 方法的应用包括流动的基本分析、降阶建模、数据压缩重建、流量控制和空气动力学优化设计。

POD 方法将流场分解为时均量和脉动量，且任意脉动量定义为模态基与时间系数的乘积总和，第i个POD 特征模态表示为：

式中，M为流场快照个数，特征值λ代表模态能量，ai(tj) 为模态系数矩阵，p′(x,tj)为第j个流场快照脉动量，POD 模态通常按照模态能量大小进行排序。具体推导见参考文献[8]。

1.3 DMD 方法简介

DMD 方法提供了一种将时间分辨数据分解为模态的方法，且每一个模态都有单一的特征频率和增长率。DMD 方法可以被视为结合了POD 和傅里叶变换的有利方面，从数据中识别时空相干结构。DMD方法起源于流体力学，由于是一种纯粹的数据驱动算法，不需要控制方程，因此在流体动力学中广泛应用。

首先假设线性映射矩阵A将流场vi映射到vi+1，即：

其中，系统矩阵A刻画了流场的时间演化特性，但A的数据量极大，因此使用矩阵A的近似值来估计其特征值。DMD 的模态可表示为：

具体推导过程详见参考文献[9]。

2 计算工况及流场计算结果

2.1 计算网格与计算工况

本文选取GLC305 翼型带944 号冰形[25]进行三维流动模拟研究。其中，944 号冰形是该翼型在结明冰的温度条件下暴露22.5 min 产生的典型双角状积冰。翼型几何如图1 所示，弦长为0.914 4 m。网格前后计算域均为20 倍弦长。采用混合网格策略，表面生成附面层，第一层网格到壁面的距离为5.0×10-6c（c为翼型弦长），网格增长率为1.1，其余用非结构网格填充。计算域远场分别设置为速度入口和压力出口边界条件，物面采用绝热无滑移边界条件，展向为周期边界条件。

计算工况：来流马赫数Ma=0.12，此时基于翼型弦长的雷诺数Re=1.8×106，迎角为α=6°。此迎角对应风洞失速点附近状态。设置非定常时间步长Δt=0.001 s，每个时间步取30 步内迭代。

首先开展网格无关性验证研究。分别采用细、中、粗三套网格，具体信息如表1 所示，二维网格如图2 所示。保持第一层网格高度不变，改变节点数量和网格增长率，总网格量分别达到6.0×106、1.0×107、1.4×107。计算结果表明，基于中网格和细网格得到的升力系数趋于一致，具体结果见表1，且与实验测量结果较为相符，因此本文选用1.0×107网格开展后续的计算分析研究。

表1 网格无关性验证Table 1 Grid convergence study

图2 带冰翼型网格划分示意图（网格无关性验证）Fig.2 The generated computational meshes of the iced airfoil for grid convergence study

2.2 计算结果

首先从时均流场结果进行分析，图3 为带冰翼型表面压力系数分布。可以看出，在带冰翼型的下表面，基于SSTk-ω湍流模型的计算结果（标记为SSTRANS）和IDDES 方法的计算结果均与实验值吻合。而对于翼型上表面，IDDES 方法计算结果明显优于SST-RANS 结果，与实验值更加贴合。具体而言，在x/c=0～0.25 处，IDDES 方法准确预测了冰角下游的压力平台（由于分离泡存在，导致此处的压力系数恒定），但SST-RANS 的结果并没有很好体现这一现象；在x/c＞ 0.25 的压力恢复区域，IDDES 方法计算的压力恢复过程相对于SST-RANS 结果向后移动，与实验值更为相符。

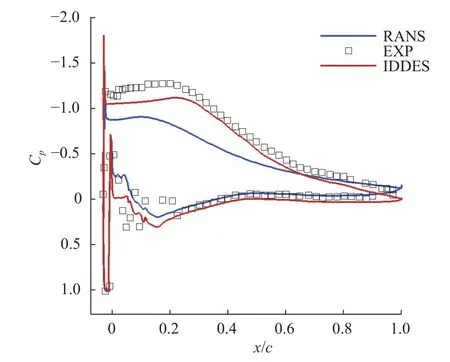
图3 带冰翼型表面时均压力系数对比Fig.3 Comparisons of the obtained time-averaged distributions of the pressure coefficient

表2 给出了时均气动力的对比（取相对稳定阶段的流场做时均）。由表可知，IDDES 方法对于宏观气动力的预测明显优于SST-RANS 方法，尤其是升力系数的预测，与实验的误差仅为5.1%。上述结果表明IDDES 方法能够准确地预测翼型表面的压力分布和气动力大小，可为后续基于数据驱动的模态分析提供准确的数据样本。

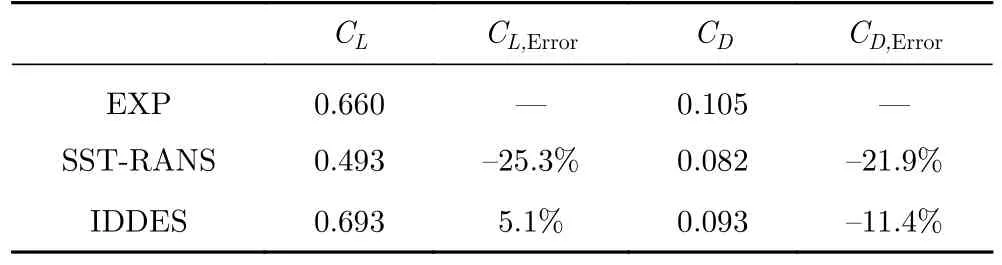
表2 时均气动力与实验值的对比Table 2 Comparisons of the time-averaged aerodynamic forces that obtained with different models

以下针对瞬态结果进行分析。图4 为基于Q准则的带冰翼型瞬时流场特征，涡结构采用湍动能染色，清晰地反映了带冰翼型上翼面冰角后方分离流的空间演化特征。具体而言，在翼型的上表面，自由剪切层由冰角的后缘脱出，由于Kelvin-Helmholtz 不稳定性形成展向的涡结构；紧接着，由于展向涡结构无法自我维持，卷起形成了不同方向的管状几何结构。管状涡在向下游流动的过程中，发生破碎、合并，使得整个涡结构更加混乱、更加复杂。继续向下游发展时，剪切层中由于强烈的逆压梯度而卷起旋涡，内部的低能分离流和外部的高能主流发生掺混，使得旋涡重新附着在翼型上表面，形成流动再附现象，如图5（a～c）所示。同时在冰角后形成分离泡，即翼型表面和分离剪切层之间的一个循环流体。

图4 基于湍动能着色的Q 准则带冰翼型瞬时流场Fig.4 Characteristic coherent structures depicted by Q-criterion and colored by turbulent kinetic energy behind the 3-D horn ice

图5 瞬态流场展向涡量Fig.5 Evolutions and distributions of the instantaneous spanwise vortices

为了进一步研究其不稳定性，对升力系数历史曲线进行了研究，如图6 所示。升力系数在一定范围内波动，表现了IDDES 对小尺度涡精确捕捉的能力，升力系数振荡具有不规则性。同时观察到大部分时间内获得的升力系数高于平均值0.693，表明这段时间气流基本附着在翼型表面。

图6 升力系数随时间的变化趋势Fig.6 Evolutions of the lift coefficient with time

利用快速傅里叶变换（FFT）得到升力系数功率谱密度（PSD）如图7，频率用无量纲数St进行归一化。使用翼型弦长作为特征长度标度，自由来流速度作为特征速度标度进行计算。通常，低频模式在机翼上产生的非定常力较大，可在升力系数中识别出低频模式。由图可知，带冰翼型升力系数出现了多个频率，主导频率为St=0.025。因此可以认为此带冰翼型在近失速的工况下出现了低频流动振荡现象。这种振荡表明了流动在失速和非失速状态下的准周期切换。对于不同翼型以及不同迎角，其低频模式的频率是不相同的[26]。为了进一步明晰带冰翼型流场中的频率特征及主要流动特征，下面结合模态分析进行研究。

图7 升力系数能谱图Fig.7 PSDs of the iced airfoil's lift coefficients

3 模态分析

针对上述非定常计算结果，分别采用POD 和DMD 方法对角状冰形下游的流动不稳定性进行研究。在流场充分发展后的稳定阶段，选取400 个流场快照，每个快照的时间间隔Δt=0.01。考虑到展向流动比其他方向流动弱得多，因此将非定常三维流场沿流向切片进行特性分析。

3.1 POD 模态分解结果

POD 方法可提取主要模态，通过获取主要模态的特征，分析对流动分离产生影响的主要因素。对POD 分解后的模态按照能量大小进行排序。前100阶模态能量占比和前100 阶累积模态能量占比如图8所示。第1 阶和第2 阶模态能量占比分别为16.16%和14.7%，为流场的主要模态。前10 阶模态能量基本包含了整个流场80%的能量，前30 阶累积能量超过整个流场90%的能量。因此，前30 阶的模态可代表此状态下流动不稳定的最主要特征。POD 分析表明，仅用少量的模态即可很好地捕捉流场中的波动，这有利于对流场数据进行显著压缩，同时也利于进行流动分析。下面对前几阶主要模态进行分析。

图8 各阶模态能量占比和累积模态能量Fig.8 Percentage of the energy and cumulative energy contributions with different POD modes

图9 给出了前6 阶POD 模态压力分布，可以清楚地看到POD 方法清晰地提取了流场相干结构。翼型上表面呈现交替相间的能量序列，在前6 阶POD 模态中，已清楚地捕捉到沿剪切层发展并向后缘传播的大波动。模态1 和模态2 由低频大尺度流动结构组成，显示在结冰翼型前缘有一个较大的涡结构，对前缘的壁面压力系数有显著的影响。3～6 阶模态均包含较小的模式结构。空间相干结构从x=0.2处逐渐出现，这种结构可能与剪切层（因Kelvin-Helmholtz 不稳定性而失稳）开始脱落有关。

图9 前6 阶POD 模态压力分布Fig.9 The first six POD modes of pressure field

图10 为快速傅里叶变换得到的前4 阶POD 模态时间系数。从图中可以看出，主要频率在1～50 Hz范围内，且存在从低频到高频多个主导频率。这意味着此类流场中，旋涡具有多样性。图10（a、b）给出了模态1 和模态2 的时间系数经过快速傅里叶变换得到的结果，据此可得高幅低频的主要成分。该模态下主要频率为f=1.5 Hz 和f=2.25 Hz，与文献[26]的剪切层拍打频率范围一致。该频率由剪切层失稳而产生，且与冰角后的分离泡密切相关。在图10（c、d）中，模态3 和模态4 对应的主导频率分别为29 Hz 和45 Hz，这说明与剪切层失稳的相关频率主要在1 阶和2 阶主导模态中，进一步证明了剪切层的拍打模式主导了此类非定常流动。

图10 通过快速傅里叶变换得到的前4 阶POD 模态时间系数Fig.10 Corresponding temporal coefficient for the first four POD mode via fast Fourier transformation

图10（c、d）中低频信号开始转变为高频信号，主导频率变为45 Hz。用分离泡的平均长度和自由来流速度对频率进行无量纲化，得到非定常无量纲数St=0.68。这与Ansell 和Bragg[26]根据各类研究总结到的规则模式的St取值范围（0.5＜St＜0.8）一致。这种规则模式源于流动再附位置附近的压力波动（主要由剪切层内的旋涡运动和涡脱落引起的）。图9 的模态3 和模态4 结果可以清晰地看到规则的旋涡脱落，更加证实了规则模式与旋涡运动有关，且规则模式的不稳定特征为分离流动的次要模式。

3.2 DMD 的模态分解结果

上述已采用POD 方法对流场进行了分析。此外，相较于POD 方法分解后的模态对应多个频率，DMD 分解后的模态对应单一频率和增长/放大率，据此可对每个模态的稳定性进行分析。因此，下文将对流场样本进行DMD 模态分析，并将DMD 和POD 方法进行对比研究。

首先进行DMD 分解，然后将DMD 模态进行排序。当前存在两种不同的排序方式[27]：1）直接使用模态振幅进行排序，这种排序的优势是计算简单、计算量小，缺点是容易受到噪声的影响而忽略初始幅值小但增长很快的信号；2）采用模态范数（表示各个模态对流场的贡献和影响）的方法进行排序，优点是容易衡量各模态对流场的贡献值，缺点是计算量比较大。考虑到本文样本量少，计算量较小，因此采用模态范数进行排序。

DMD 的模态特征值以共轭复数的形式呈现，将每一对特征值看作一个DMD 模态。图11 为DMD模态特征值的实部和虚部在复平面上的分布情况。其中，红色实心点表示在单位圆外，对应不稳定状态；空心点表示在单位圆上或单位圆内，对应周期模态或稳定模态。结果表明，绝大部分的特征值都在单位圆上。从图11（b）的局部特征值分布可以看出，红色实心点虽然在单位圆外，但十分靠近单位圆，说明不稳定模态处于弱发散状态。

图11 DMD 特征值的实部和虚部在单位圆上的分布Fig.11 The real and imaginary parts of the DMD eigenvalues on the unit circle

图12 为放大率和模态幅值之间的关系，其中红色圆点表示放大率大于0，黑色圆点表示放大率小于0 或等于0。放大率大于0 对应模态系数发散，反之模态系数为收敛状态。带冰翼型在此迎角状态下不稳定模态数占总模态数的32.25%，对应流动结构随着时间不受控制增长，从而导致流动分离的发生。

图12 放大率与模态幅值之间的关系Fig.12 Relationship between the growth rate and the amplitude

图13 为前6 阶DMD 模态压力分布。首先DMD的第1 阶模态为主导模态，对应静态模态，代表时均的压力分布，与所求流场的时均分布非常相似，因此可以作为数据集统计平均稳定性的简单验证。如果流场快照不具有收敛性，则1 阶模态与时均压力分布不符，所以证实了快照的数量足以进行当前分析。模态2 和模态3 为除去平均模态最主要的DMD 模态，主要反映翼型中段交替出现的涡结构。与POD 模态类似，涡结构开始出现的位置与剪切层开始失稳的位置相同。但是与POD 模式不同的是所识别的结构分解成了小的不规则结构，同时结构之间似乎表现出复杂的相互作用。

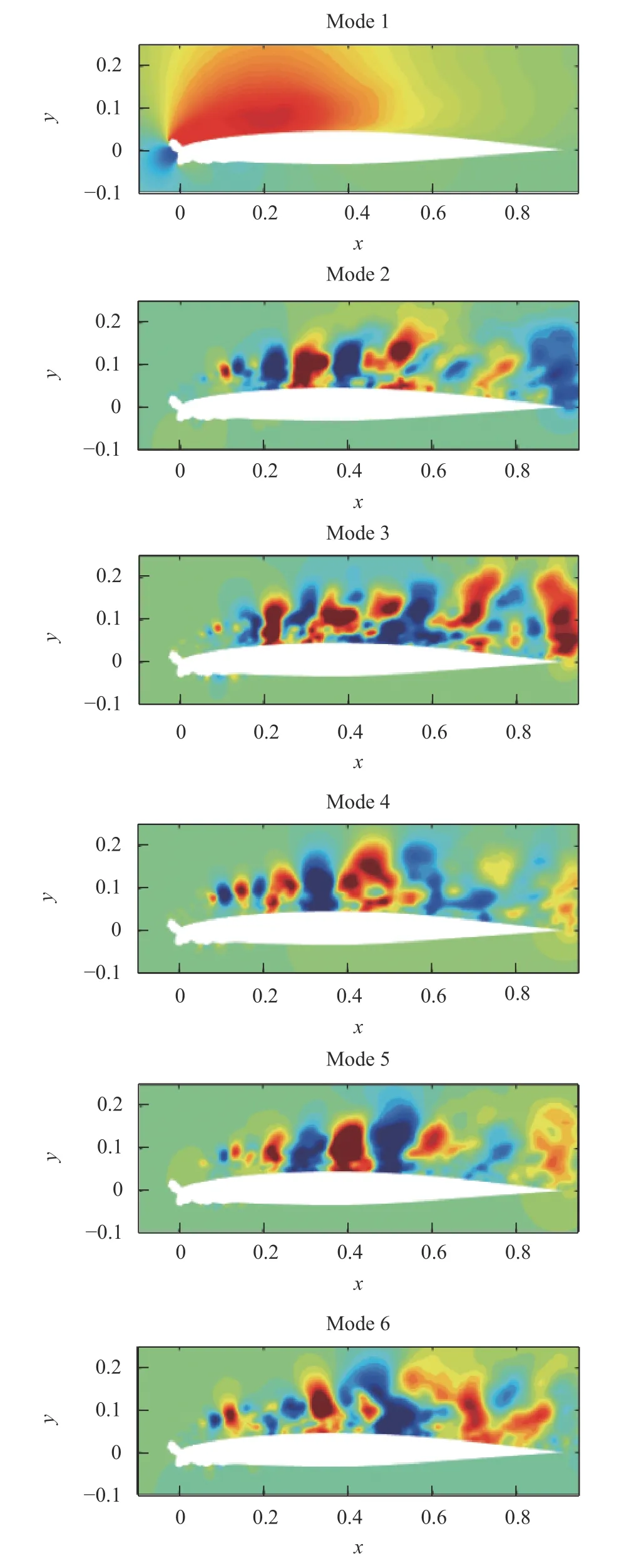
图13 DMD 模态压力分布Fig.13 The first six DMD mode of pressure field

3.3 流场重构

在结冰数值模拟多步长计算中，带角状积冰翼型的非定常流场数据量大。对此，本部分对角状积冰分解后的模态进行流场重构，为解决多步长结冰中非定常流场数据量大的问题提供参考；同时，还进一步校核两种模态分解方式对流场的提取效果。

计算中选取任一时刻的流场（本文选取t=10.74），分别使用POD 和DMD 分解后的模态对流场进行重构。其中，对于POD 方法，选择前10 阶模态和前20 阶模态加上平均流场进行重构。图14（a）为原始流场结果，图14（b、c）为POD 重构后的结果，可以看出前10 阶模态重构基本与原始流场一致，低压区的位置以及大小基本吻合。前20 阶重构结果与前10 阶相差较小，因此前10 阶模态即可还原流场特征。

图14 POD 与DMD 流场重构结果(t=10.74)Fig.14 Flow field reconstructions based on the POD and DMD methods，respectively (t=10.74)

对于DMD 方法，前20 阶模态重构的结果与原始流场差距很大，直到前300 阶模态重构才与原始流场比较接近。图15 显示了模态数和损失函数之间的关系。损失函数[27]可衡量重构流场和原始流场之间的性能损失，用于选择适当的模态数量。可以看到，前150 阶模态的损失函数小于20%，前300 阶模态的损失函数小于10%。因此，DMD 方法需要比POD 方法更多的模态数才能准确地重构流场。