高精度IPDG 湍流模拟及通量格式数值特性

郝世熙，丁秋实，魏 桐，刘正先，刘 伟，李孝检，赵 明，*

(1.天津大学 机械工程学院，天津 300350；2.电子科技大学 计算机科学与工程学院，成都 611731)

0 引言

间断伽辽金（discontinuous Galerkin,DG）有限元方法[1]是一种求解守恒系统的高精度方法，以其高精度、高紧致性、便于大规模并行计算、适于处理复杂边界、易于实现自适应等优点，成为CFD 高精度流场仿真的重要方法。

在DG 方法框架内，学者们先后提出LDG[2]、BR2[3]和内罚（interior penalty,IP）等方法进行Navier-Stokes（N-S）方程黏性项离散。其中，内罚方法将黏性项整体作为辅助变量，通过罚函数进行相邻单元间的信息交换，具有紧致性好、易实施等优势[4]。在此基础上，基于DG 方法开展雷诺平均（Reynolds average Navier-Stokes,RANS）湍流仿真成为重要的研究方向。Hartmann、Bassi 等[5-8]将IPDG 方法应用到可压缩N-S 方程模拟中，与标准k-ω湍流模型相结合，验证了该方法在RANS 湍流模拟方面的能力。

国内关于DG 方法的研究应用已经从Euler 方程拓展到可压缩N-S 方程的湍流模拟[9]。李喜乐、郝海兵等[10]结合Baldwin-Lomax 零方程湍流模型，验证了DG 方法在跨声速流动模拟中的可靠性。Yu、Yan 等[11]结合Baldwin-Lomax 湍流模型求解了二维流动问题，在激波解析方面表现出较高精度。贺立新、张来平等[12]构造了一类DG/FV 重构方法并进行了二维算例的湍流模拟。Cheng、Yang 等[13-14]将直接间断伽辽金有限元方法（direct DG,DDG）应用于RANS方程求解。张涛、吕宏强、秦望龙、陈建伟等[15-17]实现了基于S-A 湍流模型的RANS 和DES 仿真并验证了精度和收敛性，拓宽了DG 方法的应用范围。剪切应力输运（shear stress transport,SST）k-ω模型普适性强，模化精度高，在航空航天领域应用广泛[18]，但其在内罚间断伽辽金（internal penalty discontinuous Galerkin,IPDG）方法内的适用性和精度尚待研究。

与有限体积法相似的是，DG 方法也需要求解单元界面的数值通量。基于不同的近似思路，相继出现了Lax-Friedrichs、van Leer 等[19]通量矢量分裂（flux vector split,FVS）格式，同时诞生了HLL、HLLC、Roe格式[20-21]为代表的通量差分（flux difference split,FDS）格式和综合两类格式特点的AUSM 类格式[22]。在基于有限体积法的RANS 仿真中，不同通量格式表现出迥异的数值特性。例如，HLL 格式计算稳定，但是耗散较大会抹平间断。Roe 和AUSM 等格式具有低耗散特性，但会出现激波不稳定等问题[23-24]。在基于IPDG 方法的RANS 仿真中，通常会采用Lax-F、HLLC、Roe 等格式进行对流通量计算[6-17,25-28]，尚缺乏不同工况下格式特性的针对性研究。因此，应用几种代表性的对流通量格式开展IPDG 框架内的RANS仿真并结合不同格式的构造原理分析其数值表现具有一定的理论意义。

为此，本文开展了两方面工作。首先，在IPDG高精度方法框架内基于两方程SSTk-ω模型的湍流模拟，在亚/跨/超声速工况下验证SSTk-ω模型在IPDG 湍流模拟中的适用性和准确性。在此基础上，对比分析了Lax-F、HLL、Roe、AUSM 通量格式在上述湍流模拟框架中的表现。研究发现AUSM 格式在超声速工况下激波面“褶皱”现象明显，Lax-F 格式和HLL 格式鲁棒性较好，但数值精度和激波解析能力略差，Roe 格式具有宽速域内较高的数值精度和激波解析能力。

1 控制方程

1.1 无量纲雷诺平均Navier-Stokes（RANS）方程

本文基于笛卡尔坐标系下的RANS 方程组开展研究：

式中U代表守恒变量 [ρ,ρu,ρv,ρw,ρE]T，对流通量具体表示为：

黏性通量分量表示为：

式中热流率矢量为：

剪切应力张量为：

式中：黏性系数 µ=µL+µt，层流黏性系数 µL通过苏士南（Sutherland）公式计算得到，湍流黏性系数µt通过 SSTk-ω湍流模型方程计算。

1.2 无量纲SST k-ω 湍流模型方程

SSTk-ω湍流模型方程[29]综合了k-ε和k-ω湍流模型的特点，具有较好的近壁模拟能力和分离预测能力，较S-A 湍流模型适用于逆压梯度流动的模拟[30]。

笛卡尔坐标系下的无量纲化SSTk-ω湍流模型：

式中，σk、σω、β、γ 等参数 Φ通过式（8）计算得到；相应的 σk1、σω1、β1、γ1等模式参数 Φ1和 σk2、σω2、β2、γ2等模式参数 Φ2，以及 β∗、F1、F2等参数的具体计算见文献[29]。

涡黏系数计算公式为：

式中a1、Ω的具体计算见文献[29]。

1.3 松耦合求解方法

本文采取松耦合数据传递实现湍流模拟方程的求解，即独立求解RANS 方程组和SSTk-ω方程组。在上述框架内，RANS 方程组和湍流模型方程组求解采取不同精度：RANS 方程组采用高阶DG 方法求解，湍流方程组采用有限体积法求解。高阶精度的流场信息通过加权投影到湍流模型中。上述方法可以有效避免矩阵刚性带来的收敛性问题，同时规避湍流模型高精度求解的稳定性问题。

2 空间离散方法

2.1 DG 方法

记计算域 Ω的边界为 Γ，划分单元 Ωk，n为单元边界外法矢量。方程（1）通过与测试函数 φh相乘后在计算域内积分得到其弱形式：

式中：Uh表示理论解在有限元空间中的近似；为多项式阶数，uj为单元解的自由度，φj为基函数，在DG 方法内测试函数 φh取为基函数 φj。通过提高单元内多项式阶数可以实现DG方法框架内的高精度数值仿真。

2.2 内罚黏性项离散方法

由于方程含有变量梯度，采用改进的内罚函数方法进行降阶处理，构建IPDG 方法[25-26]。将黏性项作为中间变量：

约定 [·] 表示两侧值的阶跃，{·}表示两侧值的平均，定义提升算子为：

式（16）第二项中单元边界上黏性通量取为：

惩罚因子Cip建议取值范围为4 至20[5]。通过数值算例试验表明，Cip小于4 时，计算难以收敛，Cip大于20 时计算结果误差相对较大，在4 到20 之间其取值对结果影响不明显，故本文在保证收敛性的基础上将惩罚因子取为4。p为多项式阶数，hf表示面的尺度。

对IP 格式空间半离散的式（16）采取BDF2 格式进行时间离散，并采用Newton -GMRES 隐式迭代方法求解，其完整离散表达形式为：

2.3 对流通量离散格式

IPDG 方法需要求解单元界面对流项的数值通量。本文采用如下4 种格式进行计算：

2.3.1 Lax-F 格式

Lax-F 格式因构造简单而在DG 方法中被广泛采用，其构造表达式为：

式中，λ=max[(V·n+c)L,(V·n+c)R]，V代表当地单元的速度矢量，c代表当地声速，下标L 和R 分别表示单元界面两侧，F代表单侧通量。

2.3.2 HLL 格式

HLL 格式是一种近似黎曼格式，该格式采用双波假设，波速分别为sL、sR，计算较为简单，鲁棒性强。

HLL 通量表达式为：

2.3.3 Roe 格式

Roe 格式是一种经典的矢通量差分（FDS）格式。通过求解线性近似的Riemann 问题解析间断结构。Roe 格式表达式为：

2.3.4 AUSM 格式

AUSM 格式综合了矢通量分裂格式与矢通量差分格式的特点，具有数值耗散小和计算效率高的优点。AUSM 格式将无黏数值通量分解成由对流速度控制的对流项和由声速控制的压力项两部分，分别进行处理。其中，对流项部分根据逆变速度采取迎风格式，压力项部分在亚声速时包含两侧信息，在超声速时采取一侧迎风信息。

AUSM 格式的具体表达式为：

式中，总焓H=E+p/ρ。逆变马赫数和压力都分解为单元两侧之和，具体计算式为：

3 算例分析

本课题组在前期工作中基于IPDG 方法的层流仿真精度验证及数值测试体现了IPDG 在数值仿真中的高精度特点[25-26]。本文采取松耦合方式，分别求解RANS 方程及湍流模型方程，通过数据传输实现流场迭代，基于二阶精度IPDG 方法和SSTk-ω湍流模型对NACA 0012翼型进行亚声速、跨声速和超声速工况下的翼型数值模拟。具体工况参数见表1。

对半径20 倍弦长的圆形计算域划分网格，第一层网格y+=1，法向增长率1.1，边界层外网格增长率1.6（如图1 所示）。计算采用远场压力边界条件和绝热壁面边界条件。黏性项采用IP 方法处理，对流项分别采用Lax-F、HLL、Roe、AUSM 通量格式进行计算。在跨/超声速工况下，为保证激波附近计算稳定性，采用基于压力阶跃指标的人工黏性方法处理。

3.1 亚声速工况

亚声速大迎角工况下，基于SSTk-ω湍流模型的高精度IPDG 流场仿真收敛至定常解。图2 表明4 种格式在IPDG 湍流模拟中的翼面压力数值仿真结果均和实验数据吻合[32]，充分验证本文所建立的湍流仿真方法在亚声速工况下的准确性。

图2 亚声速工况4 种通量格式的翼型表面压力系数曲线Fig.2 Surface pressure coefficient curves of the airfoil under subsonic condition for four flux schemes

该工况下的翼型实验参考值升力系数约为1.45、阻力系数约为0.015。4 种通量格式计算结果基本一致，均能准确模拟流场，其中Roe 格式和AUSM 格式精度较高，如表2 所示。当地马赫数分布如图3 所示，Roe 格式计算的上翼面前缘高速区马赫数略大（图3 黑框区域），故上下翼面压差较大。

图3 亚声速工况4 种通量格式的翼型当地马赫数分布图Fig.3 Local Mach number of the airfoil under subsonic condition for four flux schemes

表2 4 种通量格式计算的升阻力系数Table 2 Lift/Drag coefficients calculated with four flux schemes

3.2 跨声速工况

跨声速工况中翼型两侧产生激波。本文建立的湍流仿真方法能够有效分辨激波结构，具备跨声速流场模拟能力。如图4 所示[33]，4 种通量格式的激波捕捉能力不同，激波分辨率和位置略有差异。

图4 跨声速工况4 种通量格式的上翼面压力系数曲线Fig.4 Upper surface pressure coefficient of the airfoil under transonic condition for four flux schemes

Roe 格式和AUSM 格式激波空间位置相对靠后，激波脚后展向速度梯度相对较大，激波分辨率较高。AUSM 格式和Roe 格式均蕴含迎风思想。

Roe 格式为避免通量雅可比矩阵特征值较小时违背熵条件所带来的非物理解，引入熵修正。但该方法带来了冗余耗散，影响边界层内计算准确性[34]。AUSM 格式对于对流项采用迎风思路而压力项则考虑了两侧贡献，较Roe 格式其更为稳定，激波分辨率更高（如图5 所示）。

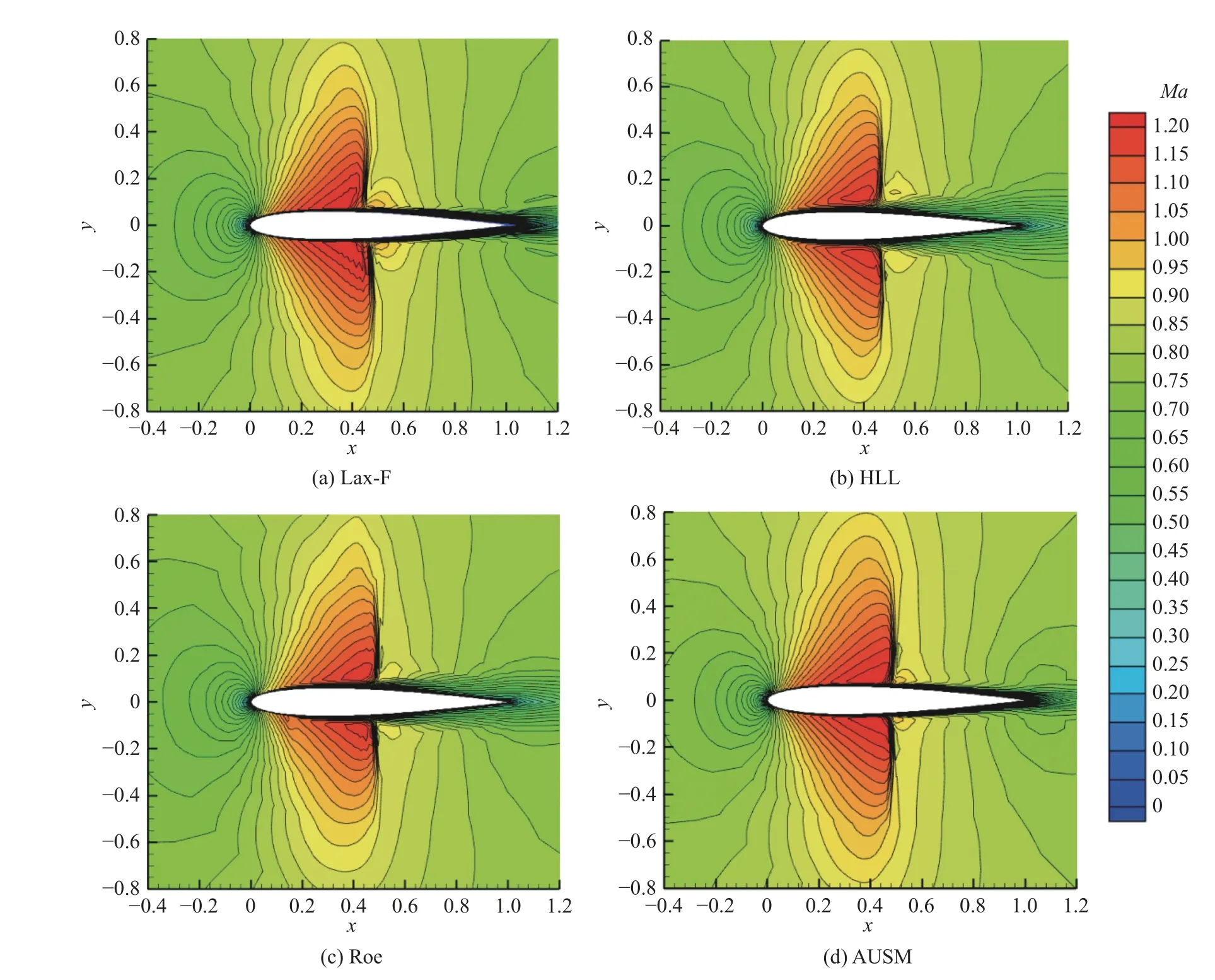
图5 跨声速工况4 种通量格式的翼型当地马赫数分布图Fig.5 Local Mach number contours of the airfoil under transonic condition for four flux schemes

Lax-F 格式和HLL 格式激波空间位置相对靠前，激波与边界层相互干扰，激波脚后展向的速度梯度小，激波分辨率相对较低。其中Lax-F 格式的数值黏性使动能耗散显著，诱导产生局部分离涡（如图6所示）。

图6 Lax-F 格式翼型中段激波脚后动能(Ek)分布云图及流线图Fig.6 Kinetic energy (Ek) contour and streamlines behind the shock foot in the middle section of the airfoil computed by the Lax-F scheme

3.3 超声速工况

超声速工况下基于4 种通量格式计算的翼型表面压力系数分布曲线如图7 所示，4 种格式的压力系数均与参考值吻合[35]，进一步证明本文建立的湍流仿真方法在超声速流动中的适用性和准确性。

图7 超声速工况4 种通量格式的翼型表面压力系数曲线Fig.7 Surface pressure coefficient curves of the airfoil under supersonic condition for four flux schemes

图8 是超声速流动马赫数等值线图，4 种格式均能准确模拟翼型头部脱体激波。Lax-F 格式、HLL 格式数值耗散大，激波面相对较光滑；AUSM 格式数值耗散小，激波面表现出“褶皱”的Carbuncle 现象，该现象通常认为是由于激波面平行方向缺少足够的数值耗散来抑制数值扰动[34]；Roe 格式激波面最为光滑。

图8 超声速工况4 种通量格式的翼型当地马赫数等值线图Fig.8 Local Mach number iso-lines of the airfoil under supersonic condition for four flux schemes

4 结论

通过松耦合-数据传递，在高精度IPDG 框架内建立了基于SSTk-ω湍流模型的湍流仿真方法，鲁棒性强。在此基础上进行亚/跨/超声速工况下的NACA 0012翼型绕流湍流模拟，结果表明SSTk-ω湍流模型在IPDG 方法中具有宽速域适用性。

比较了AUSM、Lax-F、HLL、Roe 4 种通量格式在IPDG 湍流模拟中的特性。结果表明：在低速工况下4 种格式的数值结果均与实验数据吻合，低耗散的Roe 格式和AUSM 格式精度略高。跨声速工况下Lax-F 格式和HLL 格式耗散大，激波解析能力较差，Lax-F 格式激波脚后产生局部流动分离。Roe 格式和AUSM 格式的数值耗散小，激波分辨率较高。超声速工况下AUSM 格式诱导产生明显的Carbuncle 现象。

综合来看，在IPDG 框架内基于SSTk-ω模型的RANS 湍流模拟中，Lax-F 格式和HLL 格式数值耗散大，计算稳定易收敛，但激波解析精度不高；AUSM格式在亚声速和跨声速均体现较高精度，但在超声速流动中激波面“褶皱”较明显；Roe 格式适用于本文涉及到的宽速域湍流模拟。本文采用原始AUSM格式，其修正发展的AUSM+类格式未在讨论范围，未来将进一步探究AUSM+类格式在IPDG 湍流模拟中的表现，并发展基于SSTk-ω湍流模型的转捩模式。