基于中子均方位移守恒的平均散射角余弦计算
2024-01-08秦帅李云召贺清明曹良志吴宏春
秦帅, 李云召, 贺清明, 曹良志, 吴宏春
(西安交通大学 核科学与技术学院,陕西 西安 710049)
两步法[1]是核反应堆物理工程计算中常用的计算方法,其计算精度取决于输运计算产生的均匀化群常数是否可靠。根据均匀化理论[2],均匀化前后应保证积分反应率守恒和泄漏率守恒,其中,考虑均匀化区域的各向异性散射是实现泄漏率守恒的关键条件。目前的两步法计算中,一般使用2类方法:1)产生均匀化区域的高阶散射截面,并用于堆芯输运计算中;2)产生均匀化区域的扩散系数,并用于堆芯扩散计算中。其中,扩散系数的精确计算一般需要用到高阶散射截面[3]。因此,产生精确的高阶散射截面是考虑均匀化区域各向异性散射的基础。
蒙特卡罗输运计算方法[4]几何处理能力强,基于连续能量模拟,可以直接考虑共振效应,计算精度很高,已在均匀化群常数的产生中得到了一定应用[5-8]。但是,蒙特卡罗方法在计算高阶中子通量矩时统计涨落很大,一般以中子标通量为权重计算平均散射角余弦,带来计算误差[6]。使用蒙特卡罗方法计算的高阶散射矩阵,在快中子反应堆问题中引起的有效增殖因子计算偏差达到500×10-5~600×10-5[9]。
本文提出一种基于中子均方位移守恒的平均散射角余弦计算方法,称为中子均方位移守恒法。因为计算平均散射角余弦的主要目的是保证均匀化区域泄漏率守恒,而中子的泄漏直接取决于中子在均匀化区域内的均方位移。该方法在蒙特卡罗输运计算过程中对中子均方位移进行统计,在得到中子均方位移后,计算得到使其守恒的平均散射角余弦。基于西安交通大学核工程计算物理实验室自主开发的蒙特卡罗粒子输运计算程序NECP-MCX[10]对该方法进行了实现,并使用各向异性较强的快中子反应堆问题对该方法进行了数值测试,验证了其计算精度。
1 中子均方位移守恒法理论模型
1.1 高阶散射截面与平均散射角余弦
高阶散射截面是将散射角的分布使用勒让德函数进行展开的系数矩,其定义为:
(1)
式中:r为空间变量;μ为散射角余弦;g′为入射能群;g为出射能群;Σs, g′→g(r,μ)为空间r处,以散射角余弦为μ,由g′群散射至g群的散射截面;Σs,g′→g(r)为空间r处,由g′群散射至g群的散射截面;Σs,n,g′→g(r)为空间r处,由g′群散射至g群的n阶散射截面;fn,g′→g(r)为对应能群下散射角余弦分布函数的n阶矩;Pn(μ)为n阶勒让德函数;N为展开阶数。
散射角余弦分布函数的n阶矩为:
(2)
式中:E′和E分别为中子入射能量和出射能量;Eg′和Eg为能群g′和g的能量下界;φn(r,E′)为空间r处能量为E′的n阶中子通量矩;fn(r,E′,E)为空间r处,能量由E′散射至E的散射角余弦分布函数n阶矩,其计算公式为:

(3)
式中:f(r,E′,E,μ)为空间r处,中子以散射角余弦μ,能量由E′转移至E的概率。
根据式(1)~(3),可以得到各阶散射截面。对于大多数反应堆问题,一般取展开阶数为1,一阶散射截面可以写为:
(4)
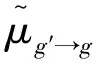
(5)
式中φ1(r,E′)为空间r处能量为E′的一阶中子通量矩。
由式 (5)可以看出,精确的平均散射角余弦计算应以一阶中子通量矩为权重,计算其分布函数的一阶矩,但在蒙特卡罗输运计算过程中,不同飞行方向的中子会发生相互抵消,导致一阶中子通量矩的统计涨落很大。因此,在传统计算中一般采取通量正比假设[11]:
φn(r,E′)=Cnφ(r,E′)
(6)
式中:φ(r,E′)为空间r处能量为E′的中子标通量;Cn为n阶对应的常数。
根据式 (6),可以直接用中子标通量代替式 (5)中的一阶中子通量矩,避免统计涨落过大的问题。但中子通量和一阶中子通量矩并不满足通量正比假设,从而引入了计算误差。
1.2 中子均方位移与平均散射角余弦
计算高阶散射截面和平均散射角余弦的主要目的是考虑中子的各向异性散射过程,最终影响中子在均匀化区域内的直线飞行距离。因此,可以根据中子均方位移守恒,计算中子的平均散射角余弦,从而避免一阶中子通量矩的计算。
1.2.1 中子均方位移计算[12]
首先,考虑单能中子在无限大均匀介质内飞行的情况。将中子由当前位置移动到下个碰撞点的过程称为中子的一次飞行,那么中子每次飞行长度l的概率分布函数p(l)满足:
p(l)dl=Σte-Σtldl
(7)
式中Σt为均匀介质的总截面。
中子在若干次飞行后的均方位移可以表示为:
(8)

根据向量运算,式(8)为:
(9)
根据式 (7),式(9)中右端第1项可以写为:
(10)
式中λ为平均自由程,λ=1/Σt。
式 (9)中右端第2项可以写为[12]:
(11)

最终,中子在n次飞行后的均方位移可以表示为:
(12)
当飞行次数确定后,中子均方位移是平均散射角余弦的函数。一般情况下,该函数在[-1, 1]单调增长,即中子平均散射角余弦越大,中子在发生碰撞后越倾向于向前飞行,其均方位移就越大。
1.2.2 平均散射角余弦的计算
根据1.2.1节的推导,基于中子均方位移守恒,平均散射角余弦的计算方法为:
1)中子经由源抽样或碰撞后进入能群g,记录其当前位置为rg,s,设置ng=0,wg=0;
2) 模拟中子输运至rg,c处发生碰撞,更新该中子在当前能群的碰撞次数ng=ng+1;
3) 为处理隐俘获,更新该中子的碰撞权重wg+1=wg+wi(wi为碰撞前的中子权重);
4) 检查中子的出射能群,若中子能群不发生改变,则回到步骤2),若中子能群发生改变或被杀死,则更新计数Ng(ng)=Ng(ng)+Wg/ng及均方位移计数Dg(ng)=Dg(ng)+|rg,c-rg,s|2·Wg/ng;
5) 若中子仍存活或已模拟中子数未达到设定值,回到步骤1),否则退出。
全部模拟结束后,不同碰撞次数下的中子均方位移为:
(13)
式中Nc为用户设定的最大飞行次数。
得到中子均方位移后,即可根据式 (12)搜索得到均匀化区域的平均散射角余弦。
需要注意,式 (12)基于无限大介质得出的,但是,在两步法计算中,经常需要计算有限几何区域的均匀化群常数。针对这种情况,本文采取的修正方法为基于该有限几何区域的材料布置建立无限大问题,然后使用通量正比假设和本文方法分别计算无限大问题的平均散射角余弦,并计算修正因子:
(14)

(15)
另外需要注意,本文计算的平均散射角余弦仅对各群自散射截面进行修正,这是因为中子发生各向异性散射时,其能量损失相对较少,更易发生在自散射中,因此仅对自散射截面进行修正即可有效改善计算精度。最终的一阶自散射截面计算公式为(忽略空间项):
(16)
2 中子均方位移守恒法数值测试
为了验证本文方法,基于蒙特卡罗粒子输运计算程序NECP-MCX开发了相应的中子均方位移统计功能。NECP-MCX为西安交通大学核工程计算物理实验室自主开发的蒙特卡罗粒子输运计算程序,已具备均匀化计算功能并在“华龙一号”启动物理试验中进行了验证[8]。
2.1 一维问题
首先基于文献[9]中的一维问题对本文方法进行测试,该问题来自文献[13]中设计的低浓铀钠冷快堆,为简化问题,对燃料区和反射层进行了打混。问题几何如图1所示,燃料区和反射层的核素组成如文献[9]所示。

图1 一维问题布置图Fig.1 Layout of one-dimensional problem
本文使用NECP-MCX连续能量模式计算参考解,并在求解过程中分别统计燃料区和反射层区的33群均匀化群常数(能群结构见表1),其中一阶散射截面基于通量正比假设得到。计算时共投入1 050代,其中前50代为非活跃代,每代投入50万个粒子。之后,使用中子均方位移守恒法分别计算了燃料和反射层的平均散射角余弦及修正因子,并对一阶自散射截面进行修正。最后,分别使用修正和未修正的一阶散射截面对该问题进行NECP-MCX多群计算。
实验室利用Axis PTZ相机,通过图像检测Rovio的像素重心,然后由坐标变换函数转化为摄像头姿态(pan,tilt)。通过支持向量机算法间接实现(pan,tilt)和固定坐标系(x,y)的转换。具体定位步骤如下:

表1 33群能群结构Table 1 Structure for 33-group
表2中给出了一维问题有效增殖因子keff的计算结果,参考解为1.147 18±0.000 03。可以看出,使用通量正比假设时,由于低估了系统的各向异性,多群计算的keff较大,使用本文方法对一阶散射截面修正后可以有效改善多群计算结果。

表2 一维问题有效增殖因子计算结果
图2为一维问题的中子通量分布比较。由于低估了各向异性,通量正比假设计算的反射层区域通量较大,而使用修正截面的计算结果则与参考解符合较好。图3中给出了一维问题的中子通量相对偏差分布,修正方法将通量的最大相对偏差由9%降低为4%。

图3 一维问题中子通量相对偏差分布Fig.3 Distribution of relative biases of neutron flux in one-dimensional problem
2.2 二维均匀堆芯问题
基于文献[9]中的二维均匀堆芯问题对本文方法进行测试,为简化问题,对燃料和反射层组件进行了打混,其核素组成与2.1小节相同。图4中给出了本问题的堆芯布置,堆芯由5圈燃料组件和2圈反射层组件组成,其中组件对边距为16.3 cm。

图4 二维均匀堆芯问题布置图Fig.4 Layout of two-dimensional homogeneous core problem
本文使用NECP-MCX连续能量模式计算参考解,并在求解过程中分别统计各位置处燃料组件和反射层组件的33群均匀化群常数,其中一阶散射截面基于通量正比假设得到。计算时共投入1 300代,其中前300代为非活跃代,每代投入50万个粒子。然后,使用中子均方位移守恒法分别计算了燃料和反射层的平均散射角余弦及修正因子,并对一阶自散射截面进行修正。最后,分别使用修正和未修正的一阶散射截面对该问题进行NECP-MCX多群计算。
表3中给出了本问题的keff计算结果,参考解为1.089 78±0.000 07。可以看出,使用修正截面可以将keff的偏差由0.007 96降低为-0.000 31。

表3 二维均匀堆芯问题有效增殖因子计算结果
图5中给出了NECP-MCX计算得到的相对裂变反应率分布。图6和图7中分别给出了使用通量正比假设和修正截面计算得到的堆芯裂变反应率相对偏差分布。可以看出,使用修正截面后,最大相对偏差由3.754%下降到-0.990%,相对均方根偏差由1.864%下降到0.612%。

图5 二维均匀堆芯相对裂变反应率分布Fig.5 Distribution of relative fission reaction rates in two-dimensional homogeneous core

图6 使用通量正比假设计算的二维均匀堆芯裂变反应率相对偏差分布Fig.6 Distribution of relative biases of fission reaction rates in two-dimensional homogeneous core calculated by using proportional flux assumption

图7 使用修正截面计算的二维均匀堆芯裂变反应率相对偏差分布Fig.7 Distribution of relative biases of fission reaction rates in two-dimensional homogeneous core calculated by using corrected cross-sections
2.3 二维非均匀堆芯问题
基于经合组织核能署(OECD/NEA)发布的钠冷快堆基准题MET-1000问题[14],本文设计了二维非均匀堆芯问题。MET-1000为中等尺寸堆芯,堆芯内装载金属燃料,组件对边距为16.247 cm。为简化问题,各类型组件使用均匀模型,组件内不同材料核素组成及体积份额见文献[14]。堆芯布置见图8,堆芯内插入控制棒,增加了系统的各向异性。

图8 二维非均匀堆芯问题布置图Fig.8 Layout of two-dimensional heterogeneous core problem
类似地,首先使用NECP-MCX连续能量模式计算参考解,并在求解过程中分别统计各位置处组件的24群均匀化群常数(能群结构见表4),其中一阶散射截面基于通量正比假设得到。计算时共投入1 300代,其中前300代为非活跃代,每代投入100万个粒子。然后,使用中子均方位移守恒法分别计算了5种组件的平均散射角余弦及修正因子,并对一阶自散射截面进行修正。最后,分别使用修正和未修正的一阶散射截面对该问题进行NECP-MCX多群计算。

表4 24群能群结构Table 4 Structure of 24-group
表5中给出了本问题的keff计算结果,参考解为0.950 61±0.000 04。可以看出,使用修正截面可以将keff的偏差由0.007 17降低为0.002 66。

表5 二维非均匀堆芯问题有效增殖因子计算结果
图9中给出了NECP-MCX计算得到的相对裂变反应率分布。

图9 二维非均匀堆芯相对裂变反应率分布Fig.9 Distribution of relative fission reaction rates in two-dimensional heterogeneous core
图10和图11中分别给出了使用通量正比假设和修正截面计算得到的堆芯裂变反应率相对偏差分布。可以看出,使用修正截面后,最大相对偏差由4.675%下降到0.920%,相对均方根偏差由2.444%下降到0.569%。

图10 使用通量正比假设计算的二维非均匀堆芯裂变反应率相对偏差分布Fig.10 Distribution of relative biases of fission reaction rates in two-dimensional heterogeneous core calculated by using proportional flux assumption

图11 使用修正截面计算的二维非均匀堆芯裂变反应率相对偏差分布Fig.11 Distribution of relative biases of fission reaction rates in two-dimensional heterogeneous core calculated by using corrected cross-sections
2.4 扩散计算结果
本文对修正方法计算得到的高阶散射矩阵进行数值测试,也对基于该方法产生的扩散系数进行数值测试。基于Inflow近似[3]和斐克定律,可得[8]:
(17)
式中:φg为中子通量;Σt,g为总截面;Dg为扩散系数。
当蒙特卡罗输运计算结束后,式 (17)中除扩散系数外各项均已知,该式成为了关于扩散系数的线性方程组,求解该线性方程组即可得到扩散系数。分别使用通量正比假设方法和修正方法产生式 (17)中的一阶散射矩阵,计算得到多群扩散系数,并基于该扩散系数对第2.3小节中的非均匀二维堆芯问题进行扩散计算,对基于本文方法产生的扩散系数进行数值测试。测试时计算条件设置与第2.3小节相同。
图12和13为基于通量正比假设方法和修正方法的堆芯裂变反应率扩散计算相对偏差分布。

图12 基于通量正比假设方法的堆芯裂变反应率扩散计算相对偏差分布Fig.12 Distribution of relative biases of fission reaction rates in core diffusion calculation based on proportional flux assumption

图13 基于修正方法的堆芯裂变反应率扩散计算相对偏差分布Fig.13 Distribution of relative biases of fission reaction rates in core diffusion calculation based on correction method
可以看出,使用修正方法后,最大相对偏差由5.092%下降到1.214%,均方根偏差由2.609%下降到0.792%。可以看出,修正方法计算得到的扩散系数更为精确。
3 结论
本文提出的基于中子均方位移守恒的平均散射角余弦计算方法,算例对该方法进行了数值测试,验证了本文的计算精度。与传统方法相比,中子均方位移守恒法的计算精度更高,可以有效降低强各向异性问题的计算偏差。
本文仅对一阶自散射截面进行了修正,下一步可对完整的高阶散射矩阵修正展开研究。
