混合神经网络的核电站故障程度评估方法

2024-01-08周桂王航彭敏俊

哈尔滨工程大学学报 2023年12期

周桂, 王航, 彭敏俊

(哈尔滨工程大学核安全与仿真技术重点学科实验室,黑龙江哈尔滨 150001)

核电站作为一个复杂非线性系统,当系统发生故障时,系统参数变化复杂,大量的数据信息会导致操作员难以及时、准确地进行决策。早期的核电站检测和诊断主要通过专家知识判断,然而该方法严重依赖专家经验,分析精度和稳定性较差[1]。随着人工智能技术的高速发展,为了提升分析的精度和稳定性,减少人为因素的影响,人工智能技术被应用于核电站的检测和诊断[2]。基于人工智能技术的故障检测和诊断方法已在核电站基准事故分类[3]、典型故障状态诊断[4]、时间序列分类[5]、故障程度预测[6]等方面开展了广泛研究。研究结果表明,基于人工智能的故障诊断技术具有较高的分析精度和效率。然而,在构建人工智能模型时,为了满足分析需求,仍需要进行大量的超参数选择。现阶段常用的超参数选择方法主要有:人工经验法、随机搜索法和网格法[7],但其难以满足高精度快速建模需求。为了弥补不足,群体智能优化算法被应用于机器学习超参数优化领域。常见的算法有粒子群算法(particle swarm optimization algorithm,PSO)和遗传算法(genetic algorithm, GA)等。GA自身的超参数选择对精度影响很大且分析结果稳定性较差[8]。因此本文采用PSO方法进行超参数优化。PSO受初始值影响较大并且容易陷入局部最优[9]。为了弥补该缺陷,本文提出了一种改进的粒子群优化算法(improved particle swarm optimization algorithm, IPSO)。该算法通过动态调整惯性权重因子及融合变异算法提升优化效果。

为了准确评估当前超参数下模型的泛化性能。本文采用交叉验证的方法对模型泛化性能进行验证。交叉验证法包括简单交叉验证、K折交叉验证、留一法交叉验证(leave-one-out cross validation, LOOCV)等[10]。简单交叉验证简单直观,计算成本较低。然而,该方法对划分方式和样本选择敏感。K折交叉验证可以减少因单次划分而引入的随机性和偏差,对于评估模型的泛化能力和选择最佳超参数组合具有较好的效果。LOOCV是一种特殊的K折交叉验证,在数据样本容量较小时具有更好的效果[11]。由于核电站具有故障数据少、运行数据敏感的特点,因此本文采用LOOCV分析模型泛化性能。

本文提出了一种基于IPSO和留一交叉验证法的深度学习超参数选择方法。以核电站冷却剂系统失水事故为研究对象,通过IPSO和LOOCV结合的方法确定了基于混合神经网络的LOCA破口程度评估模型的超参数。为了验证该方法的有效性和适用性,利用测试函数对IPSO与经典的PSO算法进行测试。在此基础上,将LOOCV与简单交叉验证方法进行对比。并利用35%破口尺寸对模型进行测试验证。

1 故障程度评估方法

1.1 改进的粒子群优化算法

PSO是一种基于种群迭代搜索的自适应优化算法。随机初始化N个粒子,每个粒子都是搜索空间中待求解问题的一个潜在解。每次迭代完采用个体最佳值pb和全局最佳值gb更新粒子的速度和位置[12]。假设在d维搜索空间中有N个粒子,第i个粒子在迭代t处的速度v和位置x分别为:

vi(t)=[vi1(t)vi2(t) …vid(t)]T

(1)

xi(t)=[xi1(t)xi2(t) …xid(t)]T

(2)

在迭代t处粒子的个体最佳值p和全局最佳值g为:

pbi(t)=[pi1(t)pi2(t) …pid(t)]T

(3)

gb(t)=[g1(t)g2(t) …gd(t)]T

(4)

在t+1代时,粒子的位置和速度更新为:

vi(t+1)=wvi(t)+c1r1(pbi(t)-xi(t))+

c2r2(gb(t)-xi(t))

(5)

xi(t+1)=xi(t)+vi(t+1)

(6)

式中:w为惯性权重因子;c1和c2是学习因子;r1和r2是均匀分布在[0,1]随机变量;t为当前时刻的迭代次数。

为了提升超参数优化的效率和精度,本文以标准粒子群优化算法(standard particle swarm optimization algorithm,SPSO)为基础,提出了一种IPSO方法。本文针对经典粒子群算法受初值影响较大,容易过早收敛和易于陷入局部最优等缺陷,提出了惯性权重因子非线性调整、粒子柯西变异的改进策略。

为了解决粒子群算法早熟的问题,本文采用非线性动态调整策略,惯性权重变化为[13]:

(7)

式中:M为最大迭代次数;wstart与wend与分别为惯性权重的初始值和最终值,通常情况下为0.9和0.4;k为控制因子,常用值为3。

相比于线性惯性权重变化方案,该策略更加符合实际迭代过程,能够有效提高算法的收敛性。本文在SPSO的基础上融合了遗传算法(genetic algorithm,GA)的变异操作,以一定的概率对粒子进行柯西变异[14]:

xi=xi+η·C(0,1)

(8)

式中:η为一个控制变异步长的常数;C(0,1)是一个由柯西分布函数产生的随机数。

1.2 留一交叉验证

在机器学习中,LOOCV使用原始样本中的单个观察值作为验证数据,其余观察值作为训练数据[15]。重复此操作,直到样本中的每个观察值均用作验证数据。由于每个样本均作为验证集进行验证,因此模型具有更好的分析性能。LOOCV的步骤如图1所示。对于包含N个样本的数据集,其将训练集分为N个大小相等的部分。当训练集的一部分都被视为验证集,剩余的N-1个部分被认为是新的训练集。对建立的N个模型,进行逐个验证。对于每个验证集,将模型的预测结果与真实标签进行比较,通过对比性能指标完成模型性能评估。最后,根据模型在留一交叉验证中的性能表现,选择最佳的超参数设置。

图1 留一交叉验证法原理Fig.1 The principle of the leave-one-out cross verification

1.3 混合神经网络CNN-LSTM

为了使得预测模型更加接近核电站实际运行情况,本文利用多个关键参数在事故初期的变化趋势作为神经网络的输入数据。基于该需求,预测模型需要能够处理高维度问题,并且具有空间和时间数据特征提取的能力。因此,针对该问题本文采用CNN与长短期记忆(long short term memory,LSTM)相结合的混合神经网络进行故障程度评估模型建模。该混合神经网络的模型示意图如图2所示。

图2 混合神经网络示意Fig.2 The diagram of the hybrid neural network

其中CNN具备局部连接、权值共享和不变性3个主要特征。相对于传统的全连接神经网络,采用局部连接的CNN具备更强的局部特征提取能力。权值共享有效地降低了网络的复杂程度,提高了网络分析效率。不变性使得CNN在处理变形数据时有很强的适应性[16]。为了进一步提升网络对时间相关信息的捕捉,本文将LSTM网络与CNN网络进行混合。LSTM是一种先进的循环神经网络,能够有效处理数据之间的事件相关性[17]。相对于传统的递归神经网络,LSTM能够更好地处理长时间序列问题,不容易出现“梯度消失”和“梯度爆炸”。

输入数据经输入层进入卷积层提取数据局部特征和空间特性后,再在LSTM层中对数据之间的时间相关性进行处理。经过空间和时间相关性处理的数据经由全连接层进入输出层并输出预测结果。

2 基于混合神经网络超参数优化的故障程度评估方法流程

为了实现在样本数量较小的情况下,准确选择合适的混合神经网络超参数,构建高精度预测模型,本文提出了一种基于IPSO和LOOCV的超参数优化方法。为了提升整体建模效率,消除人为因素对建模过程的影响,该方法首先通过IPSO方法对混合神经网络的超参数空间进行搜索优化。在此基础上,使用LOOCV对每个超参数组合进行模型性能评估。最后,根据评估结果确定混合神经网络的一组最优的超参数。主要包括以下几部分内容:

1)数据集构建。

对于发生频次较高的故障或者事故,充足的运行数据能够为深度学习预测模型建模提高足够的支持。然而,类似LOCA等事故发生频率很低,数据集样本数量十分有限。由于核电运行数据的保密性和事故数据的有限性,常用系统仿真模拟数据代替实际电厂运行数据进行研究。因此本文利用仿真模型生成有限样本数据,以验证该方法在核电站有限样本情况下进行机器学习模型超参数优化的能力。本文研究的输入数据存在较大的量级差距,为了避免出现“奇异现象”,数据需要进行归一化处理,为后续深度学习模型建模做准备。

2)深度学习模型建模。

本文基于pytroch深度学习模块完成了CNN-LSTM的混合神经网络开发,网络模型示意图如图2所示。本文设置了1个输入层,2层CNN,3层LSTM,3个全连接层和1个输出层。为防止深度学习模型出现过拟合现象,在3层LSTM层后均设置了dropout层[18]。

完成了深度学习模型架构搭建后需要选择模型的损失函数,激活函数和优化函数。本文关注的评价指标为故障程度评估的精度和稳定性,因此采用均方误差(mean-square error, MSE)作为损失函数。线性整流函数(rectified linear unit,ReLU)是本文混合神经网络的激活函数。相比于其他常用的激活函数,该函数梯度平滑,适用范围广,分析效率较高。为了优化CNN-LSTM中的权重和偏置,使用自适应矩阵优化算法(adaptive moment estimation,ADAM)最小化损失函数的值[19]。该算法能够避免随机梯度下降分析中可能出现的不收敛现象,具备更平滑的优化效果。

3)深度学习模型优化。

由于随机选择的深度学习模型超参数难以具有较高的预测精度和稳定性,因此需要对超参数进行优化。本文优化的超参数为每个卷积层的卷积核数、每个LSTM层的节点数、每个全连接层的节点数、总迭代次数、批处理大小和初始学习率。针对这种高纬度、复杂非线性优化问题,本文采用IPSO进行分析。IPSO的优化目标为LOOCV计算的最小MSE,因此适应度函数为CNN-LSTM模型故障程度评估结果的MSE。首先,随机初始化粒子的位置和速度,计算粒子适应度。判断粒子当前位置是否满足需求,如果满足需求则直接结束计算,输出超参数组合。如果不满足则执行后续计算。根据式(5)和(6)更新粒子的位置和速度,计算每个粒子的适应度。重新对粒子位置是否满足需求进行判断,如果不满足需求则继续计算,直到满足需求输出对应超参数优化结果。

3 混合神经网络的故障程度评估方法实验结果及分析

3.1 数据采集

本文以系统仿真程序RELAP5仿真结果作为实验数据,构建学习数据集。采用Sun的模型进行失水事故模拟[20]。该模型主要由反应堆堆芯、主泵、稳压器、蒸汽发生器、安全壳、环路内部管道和应急堆芯冷却系统等组成,能够对LOCA进程进行准确的模拟。核电站作为一个复杂的非线性系统,LOCA进程中系统内部物理、热工参数变化非常复杂。因此,不可能对LOCA进程中所有参数进行分析。本文参考文献[21],选取18个LOCA进程中关键的运行参数进行分析。具体的关键参数清单如表1所示。

表1 关键运行参数清单Table 1 List of key operating parameters

LOCA发生后,主冷却剂回路完整性破坏,大量冷却剂从破口处快速喷放到安全壳。该过程会导致环路内部压力和堆芯液位迅速降低,安全壳内部快速升压。环路内部的压力下降会触发应急堆芯冷却系统进而实现堆芯冷却。堆芯液位的快速下降特别是堆芯裸露后,包壳峰值温度会快速上升,进而威胁堆芯完整性。内部冷却剂循环的平衡打破会导致各个环路冷却剂温度和流量的变化,影响相应环路的蒸汽发生器状态。综上,表1所示的18个关键参数与破口尺寸大小有明显的相关性,选择这些参数预测破口尺寸具有重要的研究意义。

核电站破口故障程度评估问题中,混合神经网络模型中输入数据由上述18个参数组成,每组输入参数包含18个参数各自的一个时间序列。为了能够捕捉相同时间内更多的数据信息,每0.1 s采集一次数据。本文根据LOCA发生后70 s的瞬态数据进行破口尺寸预测,因此每个输入参数对应700个数据点。假设事故发生时,学习数据库内部仅有破口尺寸为0、20%、40%、60%、80%、100%的事故数据。其中0为环路没有破口的情况,100%为冷管段环路发生双端剪切断裂事故。为了说明故障后参数的变化情况,图3示出了在6种不同破口尺寸下主冷却剂回路压力变化趋势。当发生LOCA时,大量冷却剂从破口处快速喷放到安全壳。该过程会导致主冷却剂回路压力迅速降低。破裂尺寸越大,变化速度越快,压力值越低。

图3 不同破口尺寸的主回路压力Fig.3 Main circuit pressure for different break size

当各输入数据之间数量级差距较大时,会出现“奇异现象”,严重影响建模的精度和效率。为了更有效地训练神经网络,需要对数据进行归一化预处理。本文采用的Min-Max归一化方法为:

(9)

式中:xi(t)为数据原始值;ximin(t)和ximax(t)为xi(t)的最小值和最大值;xi(t)′为归一化后的数据。

3.2 混合神经网络模型性能测试

为了验证本文采用的CNN-LSTM混合神经网络在破口尺寸预测上的优势,将CNN-LSTM与CNN、LSTM的破口预测结果进行对比分析。由于深度学习模型的偏置和权重具有一定的随机性,为保证预测结果具有更好的代表性,各模型在相同的超参数下进行了50次预测。图4为各个模型在破口尺寸35%的50次故障程度评估结果。数据结果表明,LSTM评估精度最差,大部分评估结果都明显偏离实际值。表2为各个模型的对比分析结果,CNN-LSTM相对于CNN和LSTM在评估精度上有明显的提升。在评估稳定性上和CNN基本一致,明显优于LSTM。

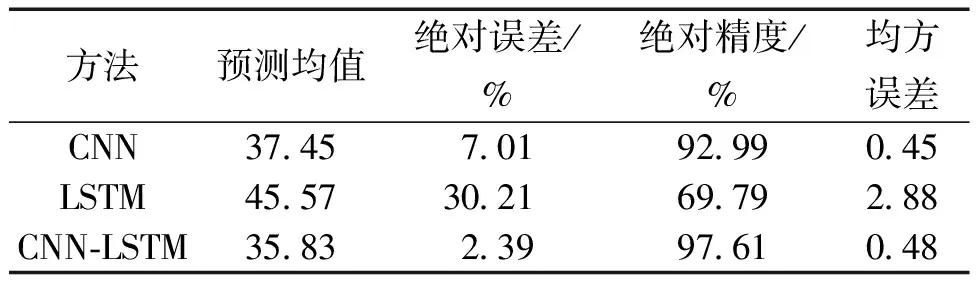
表2 破口尺寸35%预测对比分析结果

图4 破口尺寸35%的50次预测结果Fig.4 50 predictions of the break size 35%

3.3 超参数优化

3.3.1 IPSO性能测试

为了全面评价IPSO的优化性能,本文选择Sphere和Griewank测试函数对IPSO进行测试[22]。Sphere和Griewank的优化范围分别为[-100,100]和[-600,600]。种群个数设置为15,最大迭代次数取300。利用SPSO和IPSO分别对2个10维测试函数独立运行10次,测试函数的分析结果如表3所示。测试函数的寻优曲线如图5所示,其中f为适应度值。

表3 测试函数优化数据Table 3 Test function optimization data

图5 测试函数适应度Fig.5 Test function fitness

结果表明,IPSO在2个测试函数中均具有更好的寻优效果,其最优值和均值都明显优于SPSO。由方差可知,IPSO的鲁棒性同样优于SPSO。SPSO的收敛速度较快,但会陷入局部最优且无法跳出。IPSO的自适应变异保证了种群的多样性,并且采用动态调整惯性权重因子的手段,有利于粒子跳出局部最优。

3.3.2 验证方法对比分析

为了准确评估LOOCV在小样本条件下评估机器学习模型泛化性能的效果,本文利用IPSO对CNN-LSTM模型进行超参数优化,并分别用LOOCV和简单交叉验证进行模型泛化性能评估。为了保证预测结果具有广泛的代表性,每种模型在确定的超参数下进行50次预测。图6为模型在破口尺寸为35%的盲例下预测50次的结果。表4介绍了LOOCV和简单交叉验证的对比结果。数据结果表明,采用LOOCV方法评估选取的超参数组合具有更好的预测精度和稳定性。特别是预测过程中明显减少了“奇异值”的出现,为破口尺寸预测提供了更加可信的预测结果。