LHCb =8 TeV的Drell-Yan-Z→e+e-数据对部分子分布函数的影响
2020-02-19吾热卡西艾麦提阿力木阿布来提沙依甫加马力达吾来提霍文生
吾热卡西·艾麦提,阿力木·阿布来提,沙依甫加马力·达吾来提,霍文生
(新疆大学物理科学与技术学院,新疆 乌鲁木齐 830046)
质子-质子非弹性碰撞实验中,pp→Z*+X→l++l-+X过程一般称为Drell-Yan-Z(记为DY-Z)过程[1].如果末态轻子对是正负电子对,那么此过程称为DY-Z-e+e-过程,此过程的散射截面来自以下5个硬散射过程:

(1)
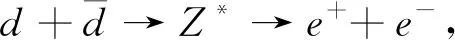
(2)
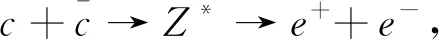
(3)
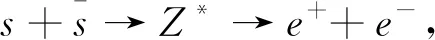
(4)
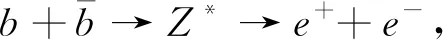
(5)
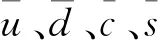
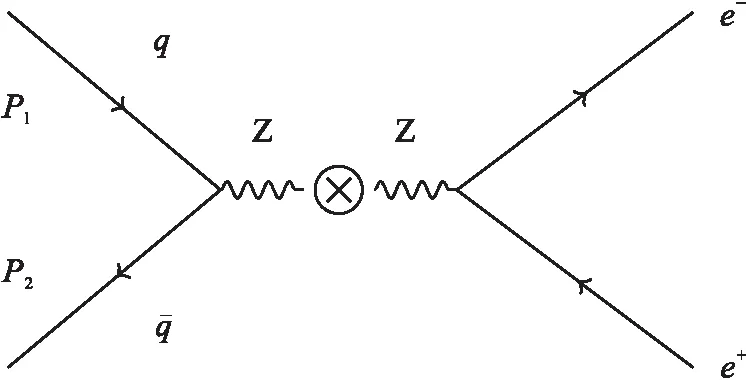
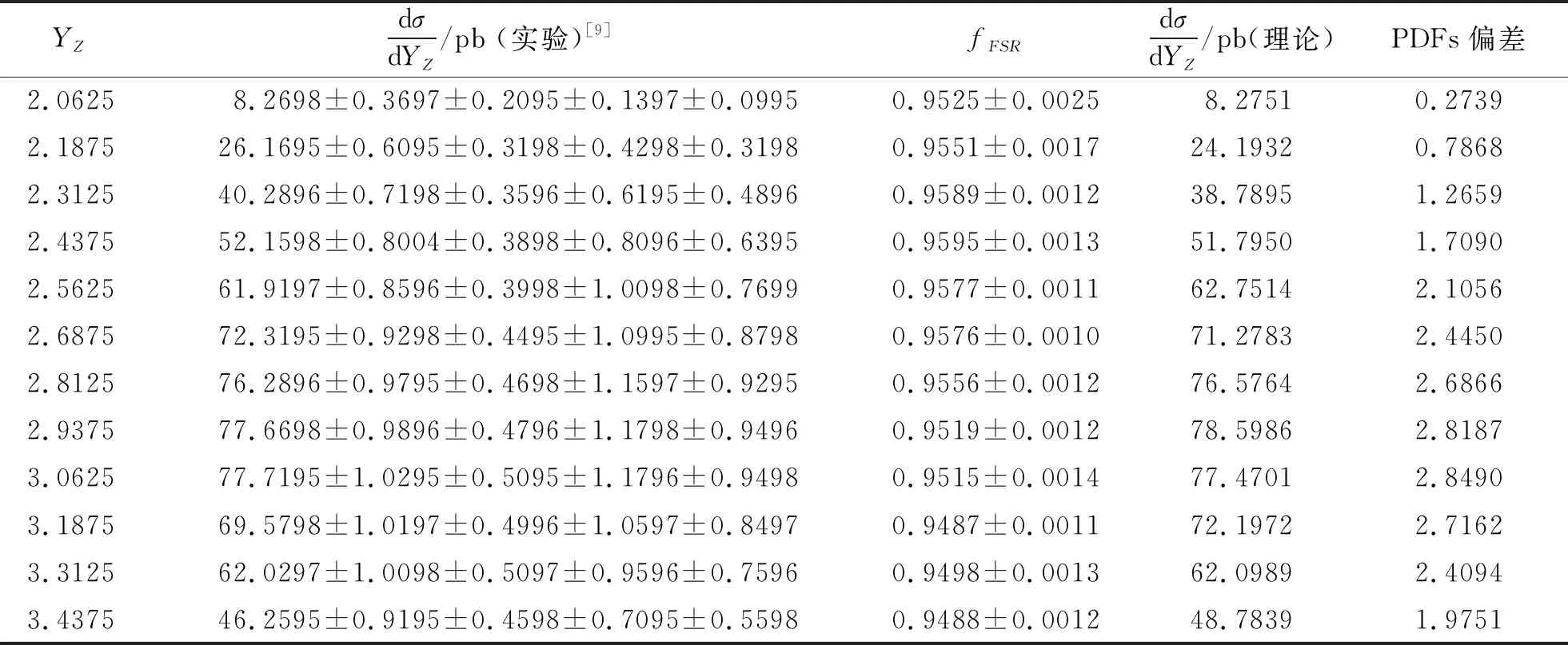
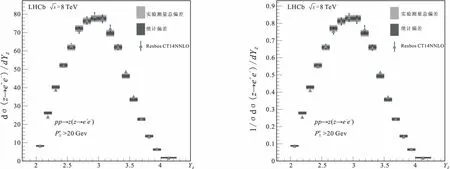
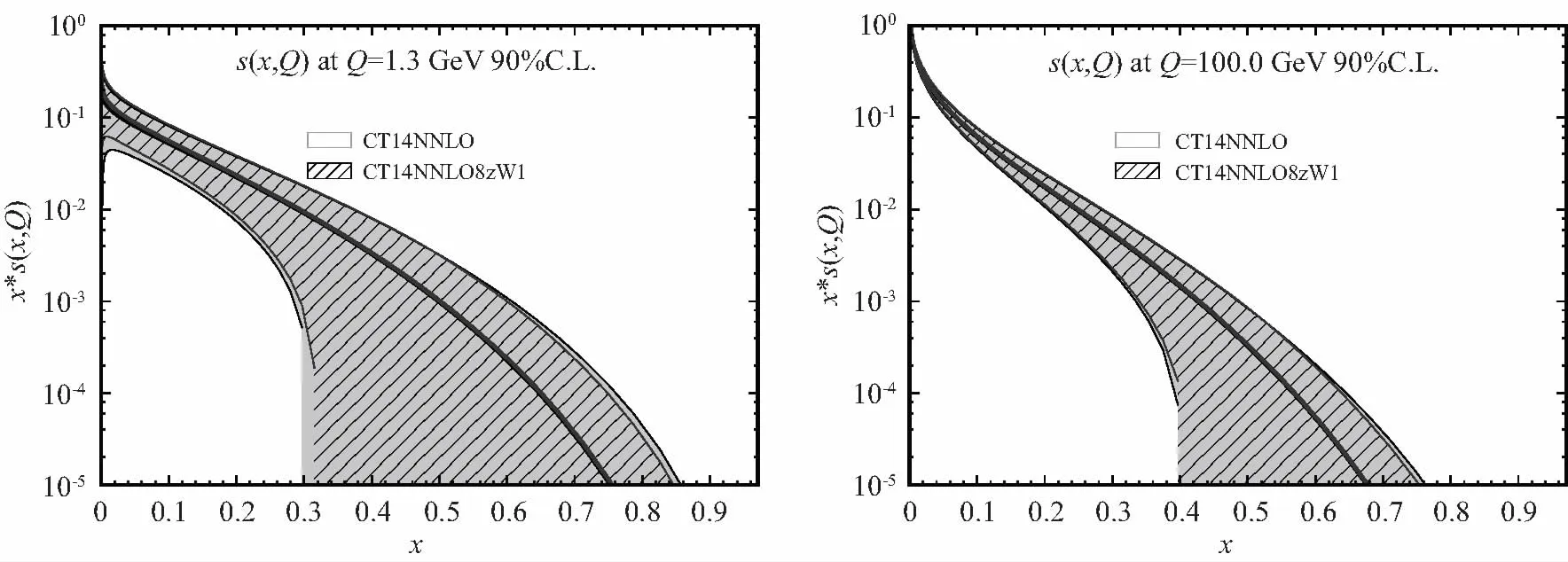
LHCb探测器已经测量了质心能量为8 TeV 的 DY-Z-e+e-过程的总散射截面和微分散射截面[9]. LHCb数据(或者加速器的亮度)的实测亮度是2.0 fb-1,虚Z玻色子的快度范围是2.0 (6) 本文的结构如下:首先,按照标准模型的费曼规则推导出DY-Z-e+e-过程的领头阶散射不变振幅和领头阶散射截面,进一步计算出一阶微扰散射截面;接下来,利用 ResBos 计算此过程的二阶微分散射截面和总散射截面,并使用 ePump 校正 CT14NNLO PDFs获取新的 CT14NNLO PDFs,然后比较新旧CT14NNLO PDFs;最后给出我们的结论. DY-Z-e+e-过程 (1)—(5) 的树图水平的费曼图如图 1所示. 图1 pp→Z*+X→e++e-+X过程的领头阶费曼图Fig.1 Leading order Feynman diagram for process pp→Z*+X→e++e-+X (7) (8) (9) (10) 其中h为螺旋度,c为夸克的颜色.经过计算,最后可以得到 (11) (12) 若进行n阶微扰计算,则计算此过程的散射截面会变得更复杂.所以我们使用了切图法(图 2),将内线切开. 图过程的切图Fig.2 Cut diagram for process 散射截面的部分子部分的领头阶散射截面可以写为 (14) 因此整个过程的总散射截面为 (15) 按上面的表达式推导部分子散射部分的一阶微扰散射截面: (16) 其中 (17) 利用 ResBos、边界条件 (6)以及 CT14NNLO PDFs算出DY-Z过程的总散射截面.理论结果见表1. 表1 σ(pp→Z*+X→e+e-+X) 的总散射截面的理论值和实验值Tab.1 Total cross section of σ(pp→Z*+X→e+e-+X) from theoretical calculation and experimental measurement 注:stat—统计偏差;syst—系统误差;lumi—亮度误差;ΔPDF[%]—PDFs误差(取百分比). 注:黑色区域内的灰色竖线是实验中心值.深灰色圆形点表示 ResBos 理论计算的中心值,单位pb.理论误差来源于PDFs 的精确度,穿过深灰色圆形点的横线表示PDFs误差. 图3 总散射截面的实验值与理论值的比较 总散射截面的实验测量值和理论计算值绘于图3.由图可见,显然 ResBos 理论中心值与实验中心值非常接近,可是理论偏差范围大于实验的总偏差范围,即PDFs的误差大于实验的总偏差.而我们需要偏差小于实验总偏差的 CT14NNLO PDFs,PDFs的偏差越小越好.因此我们用原来的PDFs 更新得到新的PDFs. 表2 pp→Z*+X→e+e-+X过程的微分射截面的理论值和实验值Tab.2 Differential cross-section of pp→Z*+X→e+e-+X from theoretical calculation and experimental measurement 续表2 图4是(pp→Z*+X→e+e-+X) 过程的Z 玻色子快度和微分散射截面的关系.图5表示过程(pp→Z*+X→e+e-+X) 的Z玻色子快度与归一化一阶微分散射截面的关系.从两个分布图中可见,第6~10个模块的PDFs偏差大于实验总偏差.从此角度来说,必须更新 CT14NNLO PDFs. 注:穿过浅灰色区域中间的横线表示实验中心值.灰色三角形点与穿过浅灰色区域中间的纵向 竖线表示ResBos 理论计算的中心值和理论计算的偏差,即PDFs的偏差. 当能量尺度Q分别为1.3 GeV 和100 GeV 时,旧的奇异夸克PDFs (CT14NNLO) 与添加LHCb 8 TeV 实验数据后更新出来的新异夸克PDFs(CT14NNLO8ZW1)的比较见图5.当添加新实验数据时,我们利用ePump升级了PDFs.从图5可知,新的奇夸克PDFs偏差比旧的奇夸克PDFs偏差好一些,因为新的奇夸克PDFs的误差小于旧的奇夸克PDFs的误差. 图5 CT14NNLO和CT14NNLO8zW1奇异夸克PDFs的比较Fig.5 Comparison of s-quark PDFs of CT14NNLO and CT14NNLO8zW1 在相同的能量尺度Q下,我们还比较了CT14NNLO和CT14NNLO8zW1 的不确定度,结果如图6所示.从图6可以发现,能量动量分数x在10-6~0.20区域内LHCb实验数据对于奇异夸克PDFs的影响非常明显,即新奇异夸克PDF的精确度比旧的奇异夸克PDF的精确度变大很多. 图6 CT14NNLO和CT14NNLO8zW1奇异夸克PDFs不确定度带的比较Fig.6 Comparison of s-quark PDFs uncertainty bands of CT14NNLO and CT14NNLO8zW1 在粒子物理标准模型的框架下,本文研究了LHCb DY-Z 8 TeV实验数据对CT14NNLO的影响.重和化尺度与因子化尺度在Z玻色子质量和条件(6) 时,利用 ResBos 算出微分散射截面、归一化微分散射截面以及总散射截面.然后根据实验数据使用ePump升级了CT14NNLO PDFs.新实验数据对于奇异夸克PDF的影响非常明显,且新的奇夸克PDF的偏差小于旧的奇夸克PDF的偏差.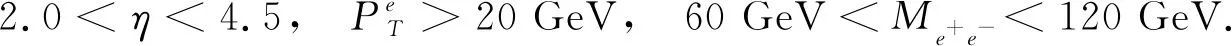
1 理论背景
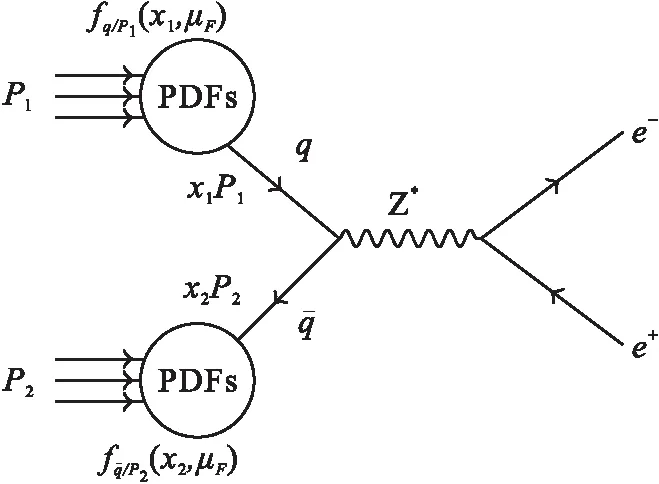

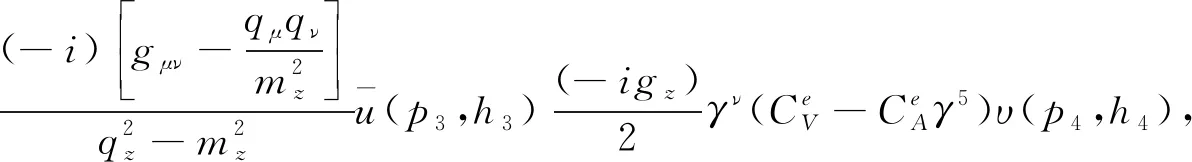

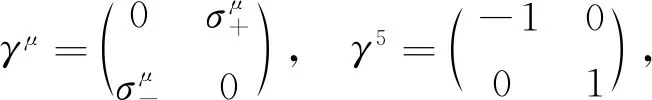
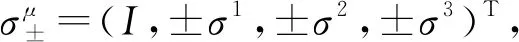

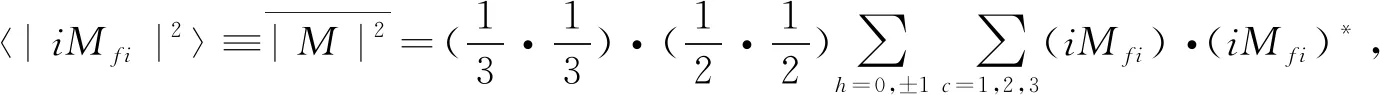
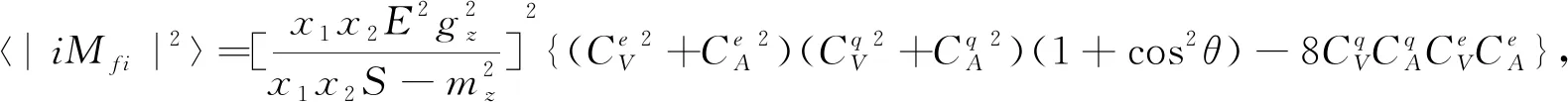

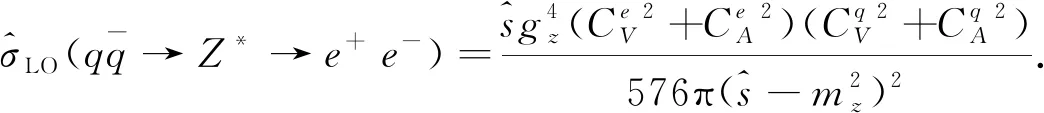

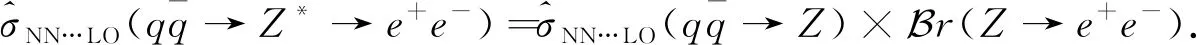

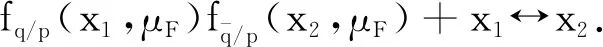
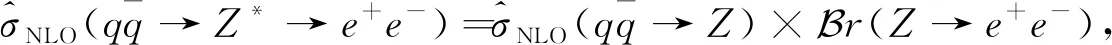
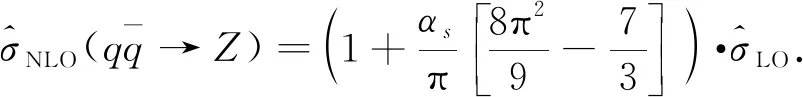
2 结果
2.1 总散射截面与微分散射截面
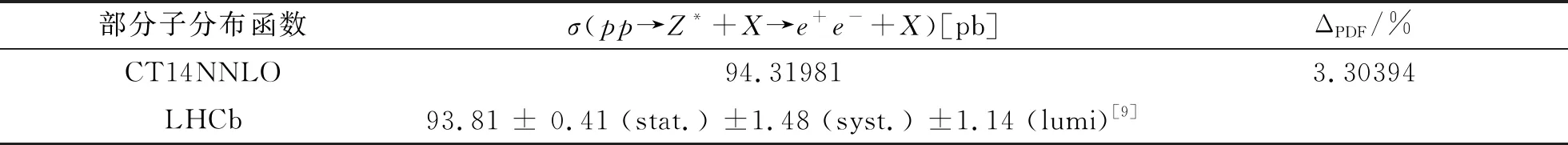

Fig.3 Comparison between experimental measurementand theory prediction of total cross section2.2 微分散射截面和归一化微分散射截面的分布分析
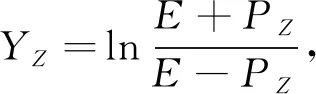

2.3 新旧CT14NNLO PDFs的对比

3 结论
