核电高压给水加热器启动过程建模与仿真
2024-01-08张志疆田兆斐
张志疆, 田兆斐
(哈尔滨工程大学 核科学与技术学院,黑龙江 哈尔滨 150001)
高压给水加热器是核电机组二回路中的重要设备,利用汽轮机抽汽加热给水,用于进一步提高机组热力循环效率[1]。高压给水加热器的仿真模型主要分为两相平衡模型和两相非平衡模型。两相平衡模型认为汽液两相始终处于饱和状态,无法准确预测给水加热器的水位[2-4]。而两相非平衡模型考虑汽液两相之间的质量和能量交换,将汽相和液相的体积作为状态变量,进而可以计算加热器的水位。另外,以往的研究通常针对入口边界条件阶跃变化等简单工况,没有针对启动过程这种大范围的瞬态工况展开研究[5-9]。当不关注金属材料的蓄热特性时,通常忽略管板和壳体金属材料的建模。但是,金属材料的蓄热特性对系统的启动时间和能量消耗有重要影响,并且金属材料温度变化引起的热应力是启动过程的重要约束条件[10]。高压给水加热器的启动过程,不仅要满足二回路系统给水的要求,同时也是对金属材料的加热过程,因此研究金属材料的蓄热特性对启动过程特性的影响有重要意义。热力系统的启动过程通常是经验性的[11],主要考虑安全因素,并未针对启动方式对启动时间和能耗的影响展开研究,启动策略相对保守。
本文以国产900 MW核电机组二回路的高压给水加热器为研究对象,建立了两相非平衡动态仿真模型。基于该模型,研究了不同抽汽阀门开度变化速率对启动过程动态特性的影响,并分析了金属材料的温度变化速率以及启动过程的能耗。
1 高压给水加热器模型简化假设
1.1 高压给水加热器结构及控制体划分
高压给水加热器结构如图1所示,其加热蒸汽为来自高压缸的湿蒸汽和汽水分离再热器的排汽,并接收来自汽水分离再热器第二级再热器的疏水。
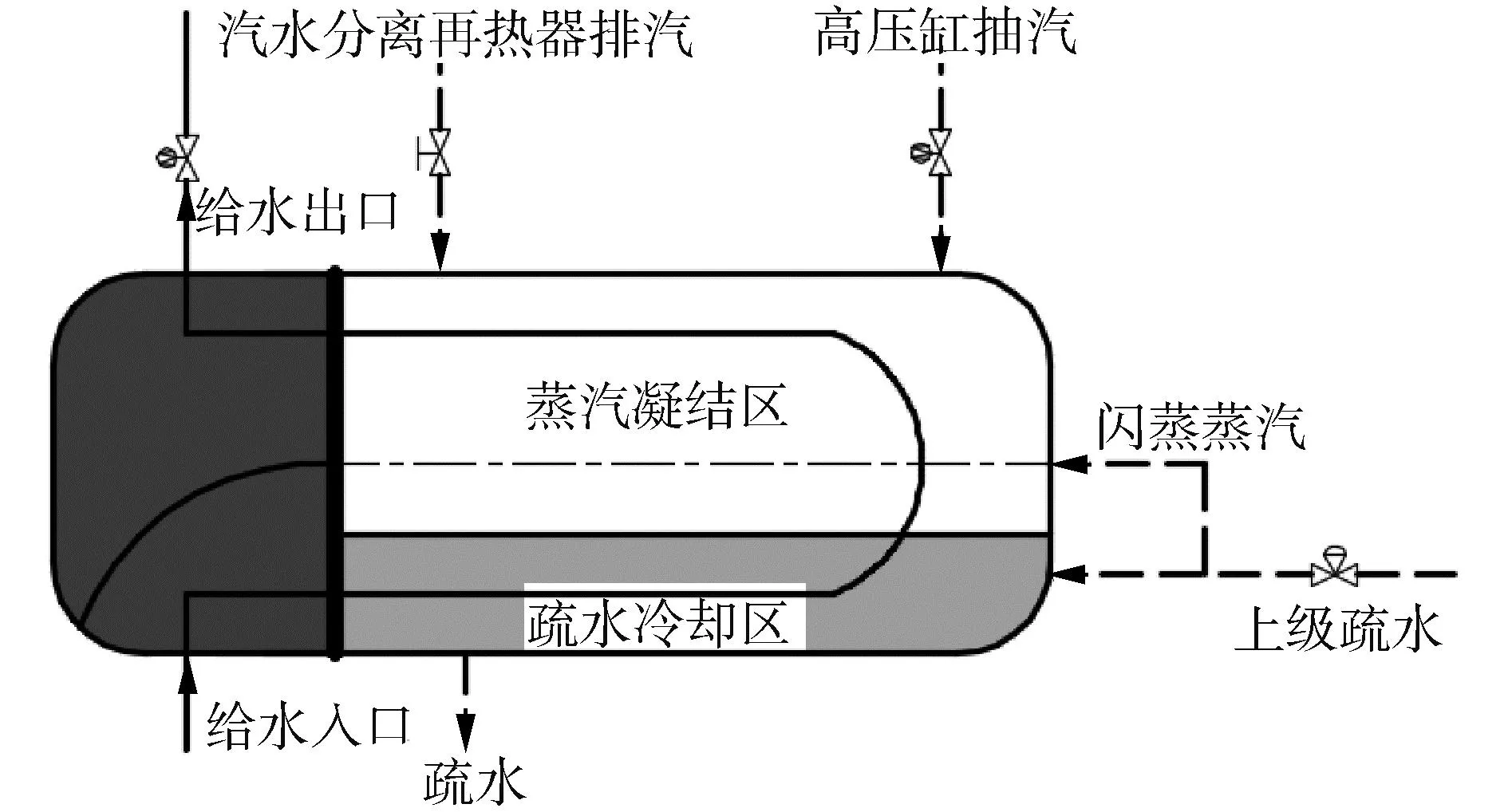
图1 高压给水加热器结构Fig.1 Structure of high-pressure feed water heater
根据壳侧工质的状态,将壳侧分为2种类型的控制体,分别是蒸汽凝结区和疏水冷却区。蒸汽凝结产生的冷凝液进入疏水冷却区,实现汽液两相之间的质量、能量交换。疏水冷却区在给水的冷却作用下,始终处于过冷状态,因此只接收蒸汽凝结区的冷凝液而不产生闪蒸蒸汽。
给水从入口水室流入给水加热器,再在U型管中流动、换热,最后从出口水室流出。因此将给水分为4个控制体,分别是入口水室控制体、出口水室控制体和U型管中的上、下2部分给水控制体,上部控制体只吸收来自蒸汽凝结区的热量,下部控制体的给水同时吸收来自蒸汽凝结区和疏水冷却区的热量。
高压给水加热器的金属材料包括壳体、U型管管壁和管板,金属材料是热流体和冷流体交换热量的媒介,并针对金属材料划分金属蓄热控制体。
1.2 数学模型简化假设
高压给水加热器无论是结构,还是涉及的物理过程都非常复杂,建立其数学模型需要做出适当的简化假设。针对给水加热器的几何结构和物理过程,作出如下简化假设[12-13]:
1)不考虑汽液两相在交界面上的传热;
2)蒸汽凝结区产生的冷凝液到达疏水液面时为饱和水状态;
3)壳侧汽相和液相工质具有相同的压强;
4)忽略不凝气体对蒸汽凝结区换热过程的影响;
5)管内给水做一维轴向流动,忽略给水的轴向导热;
6)各控制体内的流体参数均按集中参数计算。
基于以上简化假设,根据流动、换热的相关理论,可以构建出高压给水加热器的仿真模型。
1.3 边界条件
如图1所示,与高压给水加热器相连的设备有高压缸、汽水分离再热器、上级高压给水加热器和蒸汽发生器。壳侧的入口接收高压缸的抽汽和汽水分离器的疏水、排汽,出口为排向下级高压给水加热器的疏水。给水侧入口接收上级高压给水加热器的给水,出口为供给蒸汽发生器的给水。
各入口采用流量边界条件,根据控制阀门的开度控制入口流量,流量随控制阀开度呈线性变化,入口工质焓值也通过入口边界条件设置。各出口采用压强边界条件,根据稳态动量方程计算出口流量[14]。
2 高压给水加热器数学模型
2.1 壳侧工质模型
高压给水加热器壳侧分为蒸汽凝结区和疏水冷却区,蒸汽凝结区和疏水冷却的体积作为模型的状态变量,能够计算出汽液两相边界的所在位置。
蒸汽凝结区的质量守恒方程为:
(1)
式中:ρs为蒸汽密度,kg/m3;Vs为蒸汽体积,m3;Gin,s为单位时间内流入蒸汽凝结区的蒸汽流量,kg/s;Gout,s为单位时间内蒸汽凝结区的冷凝流量,kg/s。
蒸汽凝结区的能量守恒方程为:
(2)
式中:us为蒸汽比内能,kJ/kg;hin,s为流入蒸汽凝结区蒸汽的比焓,kJ/kg;hout,s为壳侧压强下的饱和水比焓,kJ/kg;Qs为蒸汽对金属材料的总放热量,kJ/s;P为壳侧压强,Pa。
上级疏水进入高压给水加热器之前,先在疏水箱内的扩散器中减压,产生的闪蒸蒸汽进入高压给水加热器蒸汽凝结区,剩余的上级疏水进入疏水冷却区。上级疏水产生的闪蒸蒸汽流量为:
(3)
式中:Gupdrain为上级疏水流量,kg/s;hsat为壳侧压强下的饱和水焓值,kJ/kg;r为壳侧压强下的汽化潜热,kJ/kg。
进入疏水冷却区的上级疏水流量、冷凝流量分别为:
Gupdrain,l=Gupdrain-Gflash,s
(4)
Gout,s=Qs/r
(5)
疏水冷却区的质量守恒及能量守恒方程为:
(6)
(7)
式中:ρl为疏水密度,kg/m3;Vl为疏水体积,m3;Gin,l为流入疏水冷却区的上级疏水流量,kg/s;Gout,l流出疏水冷却区的疏水流量,kg/s;ul为疏水比内能,kJ/kg;hin,l为流入疏水冷却区的上级疏水比焓,kJ/kg;hout,l为流出疏水冷却区的疏水比焓,kJ/kg;Ql为单位时间内疏水对金属材料的总放热量,kJ/s。
汽相和液相体积的关系为:
(8)
比内能和比焓、压强以及密度的关系为:
u=h-P/ρ
(9)
计算密度关于时间的导数时,以压强和比焓作为状态变量,可得:
(10)
式中:(∂ρ/∂P)h为密度关于压强的定比焓偏导数,(∂ρ/∂h)P为密度关于比焓的定压偏导数。
式(10)中的热力学偏导数可以通过亥姆霍兹能量状态方程导出[15-16]。例如,两相区密度关于比焓的定压偏导数为:
(11)
式中:ρ′为液相密度,kg/m3;Ts为饱和温度,K;v″为汽相比容,m3/kg;v′为液相比容,m3/kg;s″为汽相比熵,kJ/(kg·K);s′为液相比熵,kJ/(kg·K)。
将式(10)代入式(1),可得以压强、焓值和体积作为状态变量的蒸汽凝结区质量守恒方程:
∑Gin,s-∑Gout,s
(12)
式中hs为蒸汽比焓,kJ/kg。
将式(10)代入式(2)可得以压强、焓值和体积作为状态变量的蒸汽凝结区能量守恒方程:
∑(Gout,shout,s)-Qs
(13)
其中:as=ρshs;bs=hsVs(∂ρs/∂P)h-Vs;cs=ρsVs+hsVs(∂ρs/∂hs)P
采用同样的方法可以得到以压强、焓值和体积作为状态变量的疏水冷却区质量、能量守恒方程。
2.2 给水侧工质模型
给水侧工质为单相液体,各控制体的体积不随时间变化。各给水控制体质量守恒方程为:
(14)
式中:Vfw,i为第i个给水控制体的体积,m3;ρfw,i为第i个给水控制体的密度,kg/m3;Gfwin,i为流入第i个给水控制体的流量,kg/s;Gfwout,i为流出第i个给水控制体的流量,kg/s。
各给水控制体能量守恒方程为:
(15)
式中:ufw,i为第i个给水控制体的比内能,kJ/kg;hfwin,i为流入第i个给水控制体的给水比焓,kJ/kg;hfwout,i为流出第i个给水控制体的给水比焓;Qfw,i为单位时间内第i个给水控制体的吸热量,kJ/s。
将式(6)代入式(11),可得各给水控制体以压强和焓值为状态变量的质量守恒方程:
(16)
其中:
afw,i=Vfw,i(∂ρfw,i/∂Pfw,i)h
bfw,i=Vfw,i(∂ρfw,i/∂hfw,i)P
式中:Pfw,i为第i个给水控制体的压强,Pa;hfw,i为第i给水控制体的比焓。
将式(10)代入式(15),可得各给水控制体以压强和焓值为状态变量的能量守恒方程:
Gfwout,ihfwout,i+Qfw,i
(17)
式中:cfw,i=hfw,iVfw,i(∂ρfw,i/∂Pfw,i)h-Vfw,i;dfw,i=ρfw,iVfw,i+hfw,iVfw,i(∂ρfw,i/∂hfw,i)P。
相对于温度和焓值的变化速度,压强和流量的变化是快过程,因此采用稳态的动量方程来决定压强和流量之间的关系[17]:
(18)
式中:Pfw,i+1为第i+1个给水控制体的压强,Pa;K为与摩擦系数和管道几何参数有关的常数;Gfw,i+1流出第i个给水控制体的流量,kg/s。
2.3 金属材料蓄热模型
换热管、管板和壳体等金属材料的蓄热方程为:
(19)
式中:mmetal,i为第i个金属控制体的质量,kg;cmetal,i为第i个金属控制体的比热容,kJ/(kg·K);Tmetal,i为第i个金属控制体的温度,K;Qhot,i为热流体传递给第i个金属控制体的热量,kJ/s;Qcold,i为第i个金属材料传递给冷流体的热量,kJ/s。
2.4 换热模型
高压给水加热器蒸汽凝结区的换热过程为蒸汽凝结换热,主要包括蒸汽与U型换热管束、蒸汽与壳体壁面和蒸汽与管板的换热过程。
蒸汽与U型管束的换热采用Nusselt膜状凝结公式计算可得[18]:
(20)
式中:hcond为蒸汽与管壁冷凝换热系数,W/(m2·K);g为重力加速度;λl为液膜导热系数,W/(m·K);ρl为液膜密度,kg/m3;ηl为液膜的运动粘度,m2/s;N为管排数;d为换热管外径,m;Ts为蒸汽温度,K;Tw为管壁温度,K。
蒸汽与壳体内壁、管板的换热采用竖壁膜状冷凝公式计算[18]:
(21)
式中hv为蒸汽与竖壁的冷凝换热系数,W/(m2·K)。
疏水的与U型管束的换热过程为流体横掠叉排管束强制对流换热,采用Zhukauskas关联式计算[18],如表1所示。

表1 叉排管束Zhukauskas关联式Table 1 Zhukauskas correlation of cross tube bundle
疏水与壳体内壁和管板的换热采用流体外掠平板关联式计算[18]:
Nuf=0.664Ref1/2Prf1/3
(22)
给水在U型换热管中与管壁换热,采用Dittus-Boelter公式计算[18]:
Nuf=0.023Ref0.8Prfn
(23)
给水与壳体内壁和管板的换热同样采用流体外掠平板关联式计算,如式(17)所示。
壳体金属材料与空气的换热采用流体与水平圆柱的大空间自然对流换热关联式计算[18]:
Nuf=C(GrfPrf)n
(24)
式中:C为系数;n为指数。
3 高压给水加热器启动过程仿真计算
3.1 模型求解算法
由式(8)、(12)~(13)及(16)~(19)等可以构成高压给水加热器的完整数学描述,为关于壳侧各控制体压强、焓值和体积,给水各控制体压强、焓值,金属材料控制体温度的隐式常微分方程组,经过变换后可以得到如下形式的显式常微分方程组:
dx/dt=f(x,u)
(25)
式中:x为压强、焓值、体积和温度等热力学参数组成的状态变量;u为各阀门开度、入口工质的焓值等构成的输入变量。动态模型的求解采用向后差分格式求解[19],从而保证了求解的准确定和稳定性,可以求得各状态变量关于时间的动态特性。
忽略动态模型(25)中状态变量的时间导数项,就可以得到给水加热器的初始化模型:
f(x0,u0)=0
(26)
式中:x0为状态变量的初始值;u0控制变量的初始值。
模型初始化的求解实质上是求解一组非线性方程,采用改进的Powell方法[20]求解,便可以得到高压给水加热器的初始化参数。
3.2 仿真模型动态特性验证
本文以秦山二期第6级高压给水加热器为研究对象,将本文构建的两相非平衡模型计算数据与文献[13]中的实验数据进行对比,验证仿真模型的正确性。
高压给水加热器先在设计工况下运行100 s,然后给水流量阶跃增加30%[13]。从图2可以看出,所建机理模型的动态仿真结果与实验数据基本吻合,壳侧压强和给水出口温度的变化规律符合实际物理过程。在给水加热器达到稳态后,压强和温度与实验值存在一定误差,但是均保持在2%以内,证明了该模型的有效性和正确性。
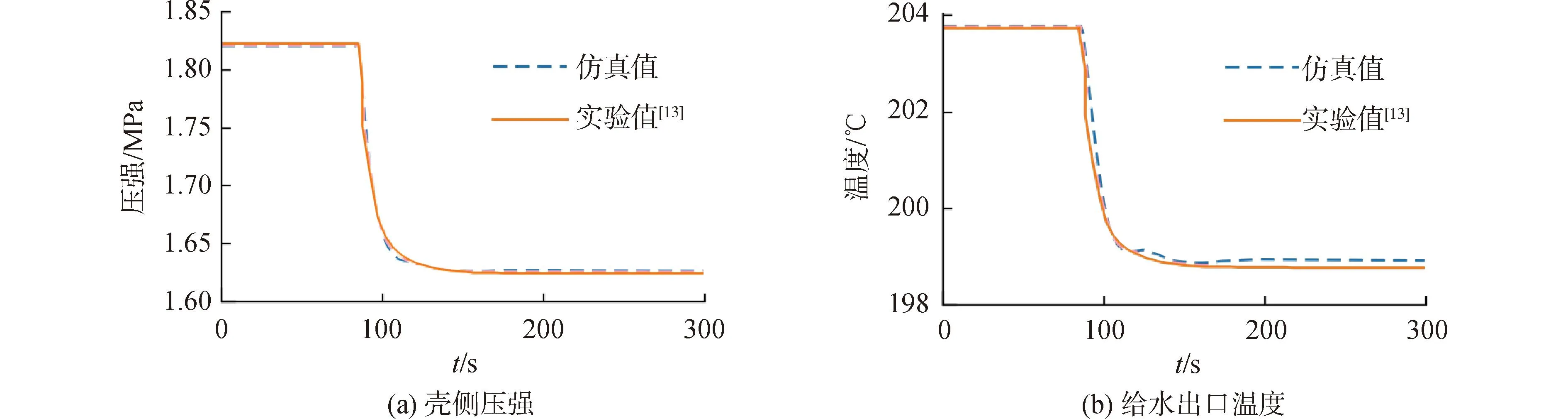
图2 给水流量增加时壳侧压强、给水出口温度响应Fig.2 Response of shell pressure and feed-water outlet temperature for feed-water flowrate increasing condition
3.3 启动过程仿真研究
以大亚湾核电站第7级高压给水加热器为研究对象,启动时给水侧已经注水,并且壳侧已经注入适当的上级疏水以保证水位。高压给水加热器变工况运行时,温度变化率不得超过55 ℃/h,最大允许温度变化速率不得超过110 ℃/h,否则会影响加热器的使用寿命[1]。
高压给水加热器的启动过程,与边界条件密切相关,而边界条件取决于系统中其他与高压给水加热器相连设备的工质热力学状态。本文中,高压给水加热器的启动采用如图3所示的方式:1)抽汽阀门开度由10%线性增大至全开状态,而抽汽焓值保持恒定,阀门开度的变化速率为主要的控制变量;2)流入加热器的上级给水焓值由372.17 kJ/kg线性增加至设计工况下的872.17 kJ/kg。
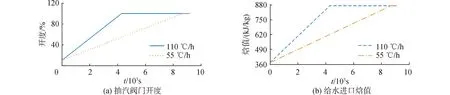
图3 入口边界条件变化规律Fig.3 Change law of inlet boundary conditions
图4所示为不同温度变化速率约束下,高压给水加热器启动的壳侧压强和水位动态特性。启动初期,壳侧压强上升的速度较慢,启动一段时间后,壳侧压强上升的速度明显增加,而压强增加又导致疏水流量增大,压强上升的速度逐渐放缓,最后稳定在设计压强附近。壳侧水位一方面受到抽汽流量增加的影响,另一方面受到压强变化引起的疏水流量和密度变化的影响。抽汽流量线性增加,所以壳侧水位的变化趋势与壳侧压强相似,但是变化速度略有不同。
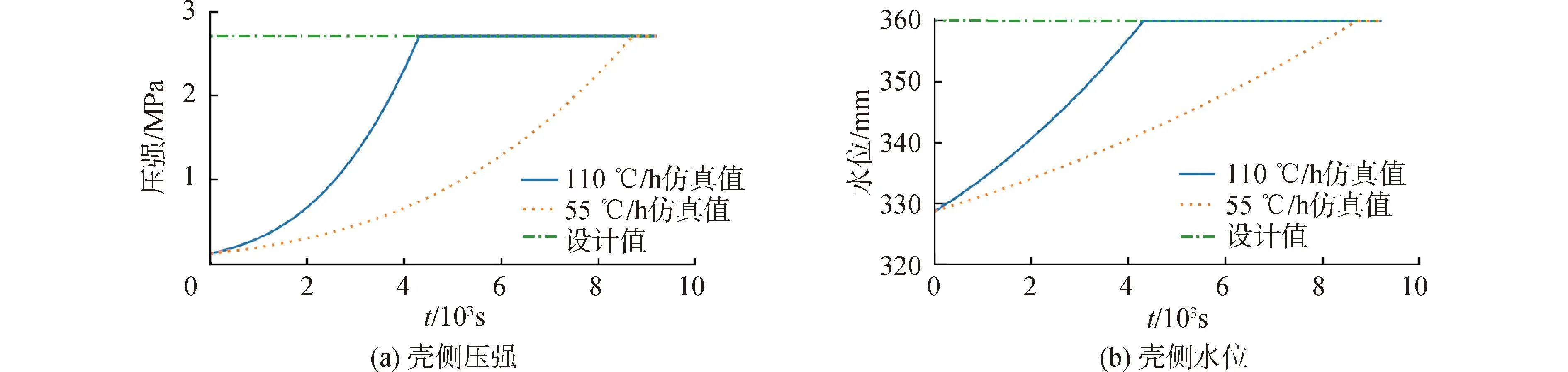
图4 壳侧压强和水位响应Fig.4 Response of shell pressure and water level
图5所示为金属热惯性对模型的影响,当忽略壳体和管板金属材料时,壳侧压强和水位的响应更加迅速,提前约200 s达到稳定状态。
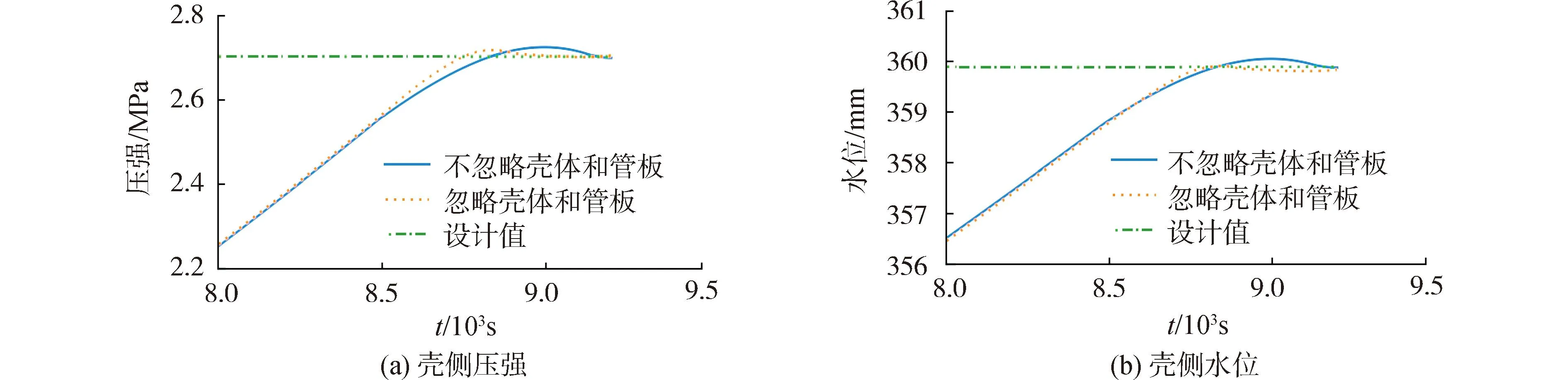
图5 金属热惯性对壳侧压强和水位的影响Fig.5 Response to feedwater pressure and flowrate
图6所示为各给水控制体在不同温度变化率约束下的压强和流量动态特性。距离给水入口越近的控制体,对入口焓值的线性变化响应越剧烈,压强的变化幅度也越大。在系统达到稳定之前,壳侧压强波动导致壳侧向给水的换热量发生变化,进而使给水压强和流量在约4 500 s(110 ℃/h)和约9 000 s(55 ℃/h)时产生波动,然后系统达到稳定状态。
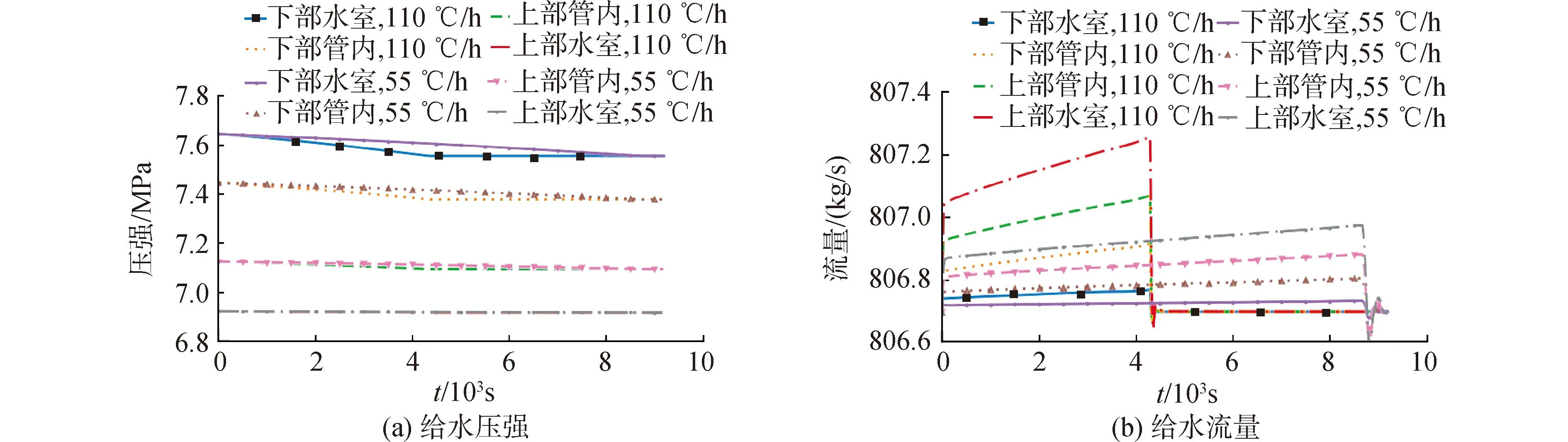
图6 给水压强和流量响应Fig.6 Response to feedwater pressure and flowrate
图7所示为给水各控制体和壳侧蒸汽、疏水的温度动态特性。随着抽汽流量的线性增加,进入壳侧的热量也逐渐增加,首先使蒸汽和疏水温度升高,然后蒸汽和疏水通过管壁向给水的放热量不断增大,使得给水温度逐渐上升至设计值。
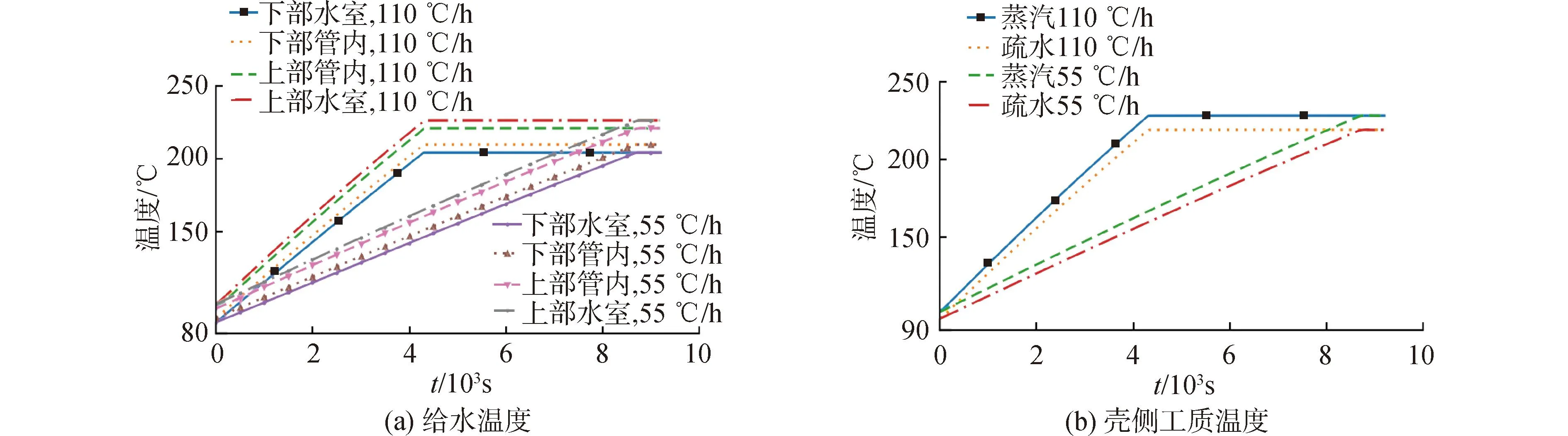
图7 给水温度和壳侧蒸汽、疏水温度响应Fig.7 Response of feedwater temperature, shell side steam and drain temperature
由图8~10可知,高压给水加热器的金属材料温度取决于入口边界条件,当抽汽阀门开度和给水焓值线型增加的速率较大时,金属材料的温度变化速率的峰值也较大。加热器刚启动和启动完成时,温度变化速率的响应较为剧烈,其他时间变化较为平缓。本文中的2种启动方式下,U型管壁、管板和壳体等金属材料的温度变化速率分别在最大温度变化速率限值110 ℃/h和正常运行温度变化速率限制55 ℃/h以下。从管板温度的动态可以看出,由于管板的换热面积和换热系数都很小,导致管板温度变化较为缓慢。
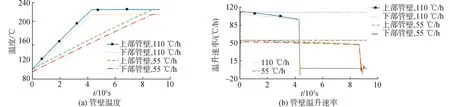
图8 管壁温度和管壁温升速率响应Fig.8 Response of temperature and temperature rise rate of tube wall
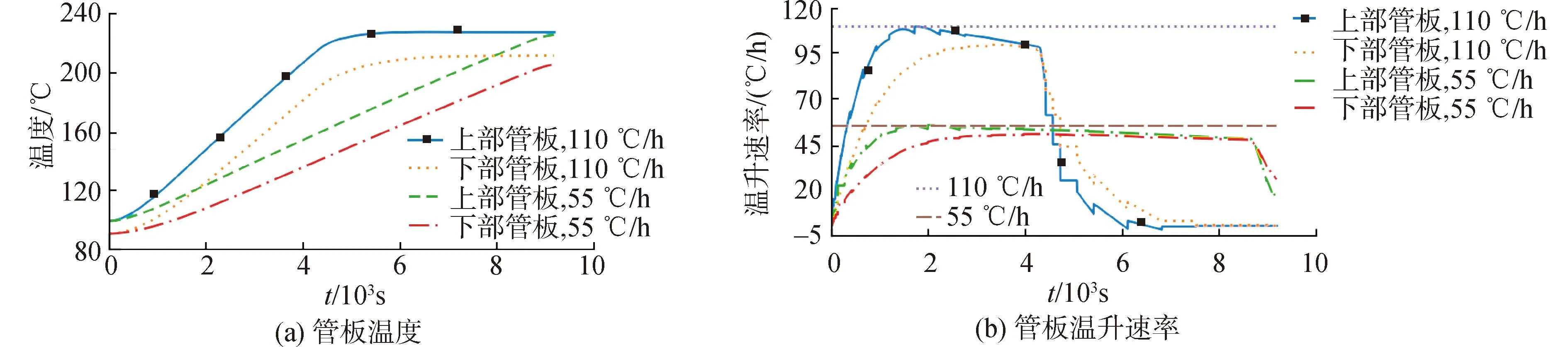
图9 管板温度和管板温升速率响应Fig.9 Response of temperature and temperature rise rate of tube plate
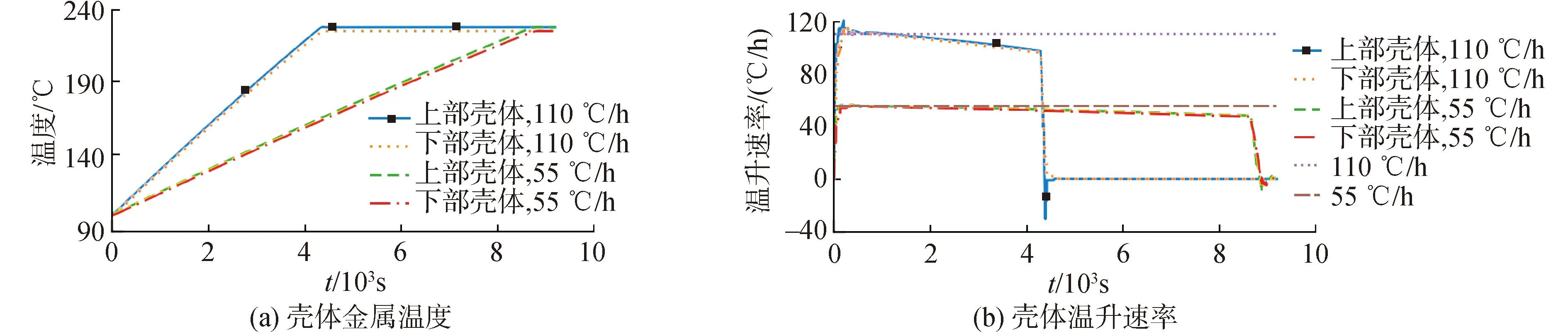
图10 壳体温度和壳体温升速率响应Fig.10 Response of temperature and temperature rise rate of shell metal
110 ℃/h变化速率约束下的启动完成参数如表2所示,高压给水加热器各参数与设计值的相对误差最高值为0.52%,证明该仿真模型具有较高的精度。
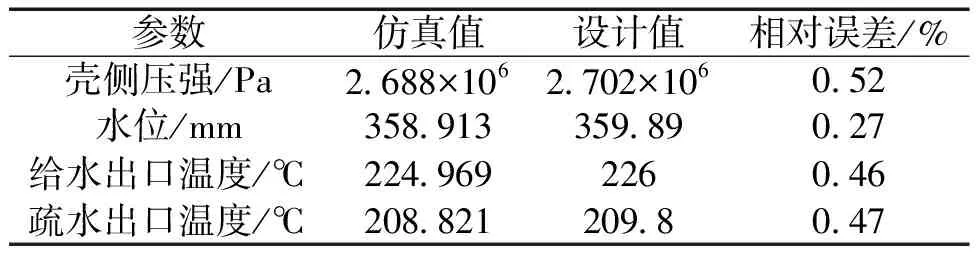
表2 启动完成后参数与设计参数对比
3.4 不同启动方式能耗及时间分析
在正常温度变化率(55 ℃/h)下启动的动态特性与最大温度变化率(110 ℃/h)下基本一致,但是在启动时间和能量消耗方面有显著区别,如表3所示。由于温度变化率的约束,抽汽阀门开度的变化速率最快不得超过75.34%/h,正常变工况运行时不得超过37.24%/h,以保证金属材料的使用寿命。正常温度变化速率下的启动时间、蒸汽消耗量和热量消耗均为最大温度变化率的2倍以上。
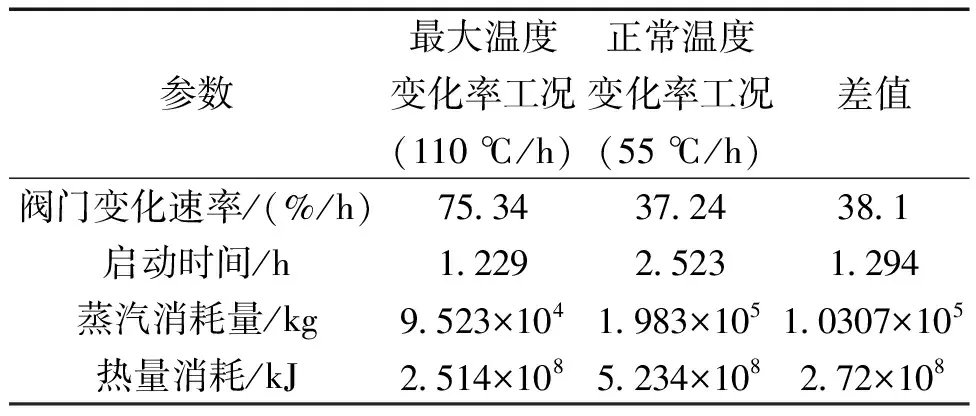
表3 不同启动方式能耗和时间对比
4 结论
1)本文仿真模型的动态特性与试验数据基本吻合,启动完成后的参数与设计参数误差较小,模型具有较高的精度。
2)金属材料的热惯性对高压给水加热器壳侧压强和水位动态特性影响较大,系统达到稳定的速度变慢。
3)本文的仿真研究表明,抽汽阀门开度的变化速率最大不能超过75.34%/h,正常变工况运行时不能超过37.24%/h,对高压给水加热器的启动过程具有重要指导意义。
本文的启动过程控制方式仍是经验性的,若要获得最优控制方式,需要进一步开展启动过程最优控制研究。
