课程标准行为动词的解读与案例分析

【摘 要】课程标准从核心素养内涵、总目标和学段目标等三个维度阐述课程目标。其中，学段目标结合具体的课程内容，通过行为动词描述数学学习应该达到的相应水平和程度。理解行为动词，有助于指导实现教学目标、明确教学知识深度、导航教学活动方向、检测教学活动质量。通过阐述对“了解”“理解”“掌握”“运用”的理解，以及进行案例分析，以期为教师掌握行为动词提供参考。

【关键词】小学数学 课程标准 行为动词 案例分析

【中图分类号】G623.5    【文献标识码】A   【文章编号】1002-3275（2023）18-16-03

在《义务教育数学课程标准（2022年版）》（本文简称课程标准）中，学生学习数学应该达到的学习水平和基本要求是依托每一节课的教学目标来实现的。准确把握每一节课的教学目标，是最终实现课程目标的关键所在。教学目标的确定以课程标准、教学内容、学生学情等为依据，通过相应的行为动词进行陈述。因此，理解课程标准中的行为动词的含义及作用，既是实施义务教育数学课程标准的前提，又是开展数学教学活动和评价数学教学活动是否达成目标的主要依据。

一、课程标准中行为动词的呈现

课程标准通过行为动词来描述学生数学学习应该达到的相应水平和程度，在第三部分学段目标、第四部分课程内容、第五部分学业质量中出现，并且附录2有关行为动词的分类对行为动词进行了专项解释和说明。在学段目标中采用相应的行为动词叙述学生在知识技能、数学思考、问题解决、情感态度等方面应该达到的学习水平。在课程内容中采用相应的行为动词叙述知识与技能、过程与方法、情感态度与价值观等三个维度的教学目标。在学业质量中采用相应的行为动词描述学生在完成课程阶段性学习后的学业成就表现。附录2把行为动词分为两类，一类是使用“了解”“理解”“掌握”“运用”等行为动词描述结果目标，另一类是使用“经历”“体验”“感悟”“探索”等描述过程目标。

二、课程标准中行为动词赋予的作用

清晰可测的教学目标对课堂教学活动十分重要。在课程标准中，制订教学目标是以知识与技能、过程与方法、情感态度与价值观等三个维度为直接依据，体现了教学目标的全面性。为了更好地表述教学目标，课程标准附录2对相关动词的含义进行说明，以发挥行为动词的指导、明确、导航和检测等作用。

（一）指导实现教学目标

课程标准中的两类行为动词是学生要达到的学习要求和水平，对教学活动具有导向作用。正如崔允漷教授提出的，“课堂教学的目标是学校教育目的范畴的一个具体概念，它在教学过程中起的作用是不言自明的：它既是教学的出发点，也是归宿，或者说，它是教学的灵魂，支配着教学的全过程，并规定教与学的方向”［1］。在课堂教学中，行为动词对教师的行为起到指导和支配作用。因此，课程标准中的行为动词不仅明确了各学段知识内容教学需要达到的水平，而且还影响着教师的教学设计、教学方法、教学策略等各个方面。

（二）明确教学知识深度

课程标准的行为动词明确规定了数学知识的范围和教学深度，对课程实施起到一种约束、限制的作用，同时为课堂教学目标指明方向，避免教学的随意性。例如小数和分数的知识在不同学段的学习要求不同。第二学段的要求是初步认识小数和分数，能进行简单的小数和分数的加减运算；第三学段的要求是理解小数和分数的意义，能进行小数和分数的四则运算。

（三）导航教学活动方向

教师在课堂教学过程中基于教学目标调整教学信息、测评学生达到的学习水平。因此，行为动词具有导航教学活动的作用。例如第二学段要求结合实例认识周长和面积，就是要求学生在具体的实例中理解周长和面积，区别周长和面积的不同。如结合数学课本的封面，能指出数学课本边缘的一周是数学课本的周长，数学课本封面的大小就是数学课本封面的面积，认识周长是相同长度单位的累加，面积是相同面积单位的累加。

（四）检测教学活动质量

课程标准是教材编写的依据，不同的教学内容要求学生达到的学习水平不同，不同的行为动词描述了学生对不同的教学内容应当达到的学习水平，使得教学目标明确、具体、可测。因此，描述学习水平的行为动词可以作为检查、测评、评估教学活动有效性的依据。

三、课程标准中结果目标行为动词的理解与案例分析

（一）对“了解”的理解与案例分析

课程标准中关于“了解”的定义是“从具体实例中知道或举例说明对象的有关特征；根据对象的特征，从具体情境中辨认或举例说明对象”。它的同类词是“知道”“初步认识”。从认知水平的程度来刻画，“知道”“初步认识”“了解”属于同一个层次。

要厘清“了解”是什么意思，可以从以下四个维度进行解读：在具体实例当中知道对象的有关特征；在具体实例当中举例说明对象的有关特征；根据对象的特征，从具体情境中辨认对象；根据对象的特征，从具体情境中举例说明对象。

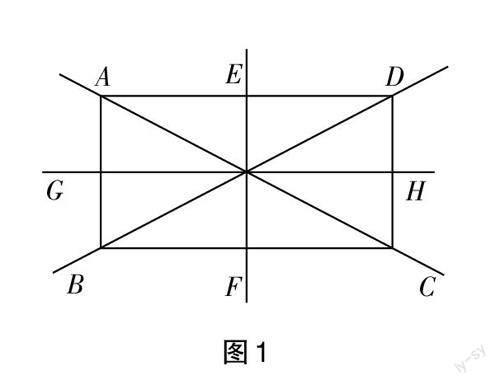
例如课程标准第二学段的具体目标包括“了解图形的轴对称”，这个目标可以描述为“了解轴对称图形的对称轴概念”。结合图1的具体实例解读“了解轴对称图形的对称轴概念”这个目标，即学生需要知道在图1中EF是对称轴，绕着EF对折，图形的两边会完全重合，即图形AEFB与图形DEFC完全重合；同样在图1中GH也是对称轴，绕着GH对折，图形的两边会完全重合，即图形AGHD与图形BGHC完全重合。根据对象的特征，从具体情境中辨认或者举例说明对象。在图1中，学生需要知道EF和GH都是对称轴，同时也要能够辨认出AC与BD不是对称轴。在这个较复杂的图形当中，辨认出哪些直线是对称轴，这就是根据对象的特征在具体的情境中辨认对象。学生做到以上两个方面，就说明他们了解了轴对称图形的对称轴概念。

再如在课程标准第二学段的具体目标中要求学生“初步认识分数”。“初步认识”与“了解”是同类词，根据“了解”的定义，学生在具体实例中要知道分数的特征，即分数的分子、分母和分数线表示的意思，根据分数的特征从具体情境中辨认分数。如对于分数[1/3]，学生要知道“1”表示分子，“3”表示分母，“-”表示平均分；在[1/3]、3、3.5、0这些数中，学生要知道[1/3]是分数；还要能结合实际举例说出分数，如把一根绳子平均分成两段，其中一段可以用分數[1/2]表示。学生知道以上分数的相关知识，说明达到了“了解”的要求。

（二）对“理解”的理解与案例分析

课程标准中关于“理解”的定义是“描述对象的由来、内涵和特征，阐述此对象与相关对象之间的区别和联系”。它的同类词是“认识”“会”。从认知水平的程度来刻画，“认识”“会”“理解”属于同一个层次。课程标准中关于“理解”的定义，可以从两个维度来解读：其一，描述对象的由来、内涵和特征；其二，阐述此对象与相关对象之间的区别和联系。

例如在课程标准第三学段的具体目标中要求学生“理解分数的意义”。这里所描述的对象是“分数”，“理解分数的意义”，即描述分数的由来、内涵和特征，阐述分数与小数、整数之间的区别和联系。从第一个维度看，学生要知道为什么要有分数。对于这个问题，学生可以从平均分的角度去说明为什么要有分数，还要知道分数是如何定义的。小学数学教材中分数的定义是把一个整体平均分成若干份，表示这样的一份或几份的数。这个表达揭示了分数的内涵（本质属性）。从第二个维度看，学生需要表达出分数与小数、整数之间有什么区别和联系。分数与小数之间的关系为分数可以化成小数，一个分数要么能化成有限小数，要么能化成无限循环小数。分数和整数之间的关系为可以把整数看成分母是1的分数。以上就是分数与小数、整数之间的关系，学生能够表达这些要点就代表他们理解了分数的意义。

再如在课程标准第二学段的学业要求中要求学生“认识直角三角形”。“认识”和“理解”是同类词，因此可以将上述要求描述为“理解直角三角形的概念”。学生要达到什么样的学习水平才能称为理解直角三角形的概念呢？根据“理解”的意思，可以从两个维度来理解：第一个维度是描述对象的由来、内涵和特征，实际上就是描述直角三角形的定义。直角三角形内角之间的关系为两个锐角的和等于一个直角，这也是直角三角形所具有的特征。第二个维度是描述直角三角形与其他三角形之间的关系。基于角对三角形进行分类，可以分为锐角三角形、直角三角形和钝角三角形，这就是它们之間的关系。学生能够描述以上两个维度就达到了“认识直角三角形”的要求。

初步认识直角三角形与认识直角三角形有什么区别呢？它们在认知水平的刻画上不一样。初步认识直角三角形属于了解的层次，主要是从具体实例中知道或举例说明对象的有关特征，根据对象的特征从具体情境中辨认或者举例说明对象。显然，初步认识直角三角形不需要达到描述直角三角形的由来、内涵和特征的要求，也不需要阐述直角三角形与其他三角形之间的区别和联系。

（三）对“掌握”的理解与案例分析

在课程标准中，关于“掌握”的定义是多角度理解和表征数学对象的本质，把对象用于新的情境。“掌握”的同类词为“能”。从认知水平的程度来刻画，“能”与“掌握”属于同一个层次。可以从三个维度理解“掌握”的意思：第一个维度是要多角度理解数学对象的本质；第二个维度是多角度表征数学对象的本质；第三个维度是在新的情境中应用数学对象。由此可见，理解、表征这两个维度都要从多角度、多维度出发。

在小学数学学习中，常用的表征方式有五种。一是用实际情境表征，根据数学对象，用一个实际情境把它表征出来；二是用图像表征，用图、表格等形象化的手段表征数学对象；三是操作表征，用行为动作来表征数学对象的本质；四是用口语符号表征，即用口语表达来表征数学对象；五是用书写符号表征。

例如对于乘法口诀“三五十五”，怎样在理解的基础上进行多角度的理解和表征？一是描述一个具体的情境进行表征，例如每行有五个圆圈，有三行这样的圆圈，或者每列有三个圆圈，有五列这样的圆圈。二是用图像表征，出示符合情境表征的图像（见图2）。三是操作表征，可以让学生用小棒摆出3×5＝15的算式。四是用口语符号表征，以5个3相加或者3个5相加来表征，或者3乘以5或者5乘以3来表征。五是用书写符号表征，可以用乘法算式（3×5＝15或5×3＝15）来表征，也可以用加法算式（5+5+5＝15或3+3+3+3+3＝15）来表征。由此可知，只要抓住对象的含义，就可以从不同角度进行理解并从不同角度进行表征，这就是“掌握”的含义。

（四）对“运用”的理解与案例分析

在课程标准中，关于“运用”的定义为基于数学对象和对象之间的关系，选择或创造适当的方法解决问题。它的同类词是“证明”“应用”。由定义可知，只有掌握对象，才可能根据它的关系选择方法去解决问题，或者创造出新的方法解决问题。因此，“运用”是在“掌握”基础上更高一个层次的认知水平，在掌握的基础上才能进行运用。

课程标准中第三学段数与运算中要求学生“能判断一个自然数是否是质数或合数”。例如关于53是质数还是合数这个问题，要根据质数与合数之间的一些关系来解决。方法一为根据质数的概念先用比53小的数去除，接着考虑是不是整除，还有因数、因数的个数等这些与质数概念相关的数学对象。方法二为只要用53除以比它小的质数，如用2、3、5、7这些质数去除53，然后根据是否整除判断因数的个数。方法三为只要除以10以内的质数，因为53如果能够分解成两个因数的乘积，那么这两个数不可能都大于或等于10。这些不同的方法都是关于质数这个对象与其他数学对象之间的关系，而方法的不同则体现了不同的运用水平。

核心素养导向下的教学目标是教学活动的出发点、落脚点和着力点。因此，理解课程标准中的结果行为动词，正确使用行为动词表述学习水平层次，才能真正发挥教学目标的导向作用，帮助学生发展核心素养。

【参考文献】

［1］崔允漷．教学目标：不该被遗忘的教学起点［J］．人民教育，2004（13/14）：17.

谢秋云 / 贺州平桂区公会镇中心学校，高级教师，从事小学数学教学（贺州 542800）