利用直观模型培养学生几何直观素养的实践探究

摘 要：《义务教育数学课程标准（2022年版）》对几何直观这一核心素养进行重新的界定与修订，其重要地位是毋庸置疑的。文章以直观模型为着眼点，结合具体的教学案例展开阐述，致力于激发学生的直观感知，引发学生直观体验，启发学生进行直观洞察，从而达到促进学生数学思维顺利进阶，有效培养学生的几何直观这一数学学科核心素养的目的。

关键词：小学数学；几何直观；几何模型；教学策略

中图分类号：G427                                文献标识码：A                                       文章编号：2097-1737（2023）32-0073-03

何为几何直观？顾名思义，就是几何与直观。几何直观不但包含运用图形或图表这两种几何形式将抽象的不同领域数学知识进行直观的表征，而且还包含几何图形本身元素的内容。众多实践表明，学生学习数学时如果有几何直观的辅助，就能有效地降低数学的抽象难度，将内隐的数量关系外显化，加深对抽象数学概念的理解，加强对枯燥算理的掌握和对复杂数量关系的明晰等，让数学思维看得见，让解题思路可视化。下面，笔者根据自己多年来对几何直观素养培养的专题研究阐述几点浅显的观点。

一、学生几何直观素养培养存在的问题

小学数学几何直观作为学生的一种思维方式、一种数学素养，在日常的教师教学过程中或多或少地存在一些问题，分析这些问题所产生的原因，笔者认为源于以下三个方面：

（一）学生几何直观操作空间过窄

当前，在很多小学数学课堂上，教师在实施教学的过程中会单向性地运用几何直观进行教学，并不重视给学生提供自主实践操作的空间，导致对学生几何直观素养的培养也只是停留于形式，并不能实质性地培养学生的几何直观素养[1]。例如，部分教师在教学人教版数学五年级（下册）“认识长方体”一课时，只是运用课件展示生活中常见的长方体物品图片，让学生通过直观观察长方体图片，总结出长方体的特点。这样，学生对长方体的特点只是停留于视觉层面，不能对长方体的特点有一个深刻的认知与理解。几何直观实践操作空间过窄，不利于学生真正建构长方体的概念，也不利于对学生几何直观素养的培养。

（二）学生的几何概念认知不全面

小学生思维尚处于以直观形象为主的阶段，如果教师在教学几何图形时呈现的图形过于单一，学生往往会产生思维定式，这在一定程度上会影响学生对几何概念的认知[2]。例如，在讲解“梯形”这个知识点时，如果教师所呈现的图形都只是单一的“上窄下宽”的梯形，那么学生就会产生“梯形就是一种上窄下宽、上下底互相平行的四边形”的思维定式。之后，学生在看到直角梯形、上宽下窄的梯形时，往往会产生困扰。由此，在教学几何概念时，教师要慢节奏、多维度、变式性地呈现图形，让学生正确而全面地认知和理解几何概念，为学生几何直观素养的培养奠定基础。

（三）几何图形内部联系分析过少

小学数学知识内部存在着千丝万缕的联系，尤其是几何图形。要想培养学生的几何直观素养，教师需要引导学生分析图形之间的联系。然而，在实际课堂教学中，有的教师往往较少引导学生分析图形之间的联系和区别，导致学生辨别不同几何图形之间的差异的能力较弱，从而直接影响对学生几何直观素养的培养。

二、学生几何直观素养培养的实践路径

基于当前教师在培养学生几何直观素养所存在的问题分析，笔者认为教师可以灵活地运用数学直观模型来培养学生的几何直观素养。同时，小学生的思维正处于由直观形象思维向抽象逻辑思维过渡的阶段，他们的主导思维还是直观形象，因此就会存在学生形象直观思维与数学知识抽象之间的矛盾。而直观模型则是打通学生形象思维与数学抽象思维之间的桥梁。教师借助几何直观这一手段，能有效地促进学生展开丰富的联想与想象，让学生通过直观模型的外形直观洞察它存在的数学规律、数学概念和数量关系等，发展学生创造性思维能力[3]。基于这样的认知，教师在具体课堂实施过程中，应适时、适当地渗透一些典型的几何直观模型，让学生形成几何直观观念，继而在一定程度上促进对学生的几何直观素养的培养。笔者认为，小学阶段应重点渗透以下三种几何直观模型：

（一）利用数轴模型，培养学生的几何直观

一提起数轴，人们都会固执地认为这是初中才学习的内容，殊不知小学数学教材编排中就已经开始有所渗透。對于“数的概念”，小学生总是难以理解其本质意义，而利用数轴这一几何模型，学生能直观地理解数的概念，不但可以培养数感，而且能发展几何直观素养。

以人教版数学二年级（下册）“近似数”一课为例，由于学生是第一次认识近似数，所以他们对近似数概念的认识还只是停留于一种浅层意义上，教材例题也是用数轴呈现（如图1），让学生建构近似数的意义。然而，在教学中，很多教师并没有充分发挥数轴的重要作用，而只是让学生直观感知“因为9985接近于10000，所以10000是9985的近似数”，并没有继续深挖与追问，导致学生对近似数的本质意义还存在着一定的认知模糊。为了深刻揭示“近似数”的本质意义，笔者充分利用数轴，帮助学生真正理解“近似数”的内涵。当学生直观得出“10000是9985的近似数，知道生活中有时不用准确数，只用近似数就可以”之后，笔者再出示9460，让学生说一说它的近似数是多少，有的学生说是9000，还有的学生说是9500。接着，笔者让学生根据数轴说出理由。一个学生能根据数轴自信地说出：“很明显，根据数轴，9000与10000的中间数是9500，而这个9460是在9500的左边，所以更接近9000，它的近似数是9000，而不可能是10000；相反，如果数据是在9500的右边，也就是9500至10000之间，那么它的近似数才是10000。”另一个学生又说：“9460的近似数取9500更好，因为9500更接近于9460本身这个准确数。”紧接着，全班学生一起交流得出：确定一个数的近似数，要根据实际需要，尽量取最接近于准确数本身的数。最后，笔者让学生以小组为单位，互相列举数据并说出其近似数。显然，这样的课堂教学能充分利用教材文本资源，发挥数轴这一几何直观模型的充分作用，让抽象而枯燥的数学概念变得直观而形象，不但培养了学生的数感，而且有效地发展了学生的几何直观素养，为学生今后进一步学习“四舍五入”法做好了充分的铺垫。

（二）巧用线段图模型，培养学生的几何直观

线段图这个几何直观模型一直以来深受小学数学教师青睐。人教版教材的编排遵循学生的思维发展规律而进行了慢节奏、渐进式线段图模型的呈现[4]。其中二年级（上册）“解决问题”一课中，当教材出示“三班小红旗比一班少4面，三班得了多少面”题目之后，先是让学生分析题意“知道了什么”，再用线段图模型表征“怎样解答”（如图2）。很显然，教材编者基于二年级学生的思维特点，先是用画小红旗的方法表征一班的数量，再用条形加文字的形式表征与一班同样多的部分，紧接着用大括号标出少的4面，最后在条形中用问号表示要求的问题。这已经为进一步建构线段图模型做好了铺垫。在二年级（下册）的“混合运算解决问题”一课中，教材出示了题目“面包房一共要烤90个面包，已经烤了36个。如果每次能烤9个，剩下的还要烤几次”，之后在“你知道了什么”这一环节直接让学生用图示表征已知条件与问题（如图3）。相较于二年级（上册）教材，教材在这里直接用方条来代替实物，如果说上册教材用实物侧重于形象直观，而这里则是半抽象了，是介于实物图与真正线段图的中间地带，能让学生直观地看到数量之间的关系。到了三年级（上册）的“解决问题”一课，教材在出示问题之后，在“分析与解答”中（如图4）直接运用线段图表征题中的已知信息与问题，让学生对数量关系有一个直观的理解。教材循序渐进的编排方式充分尊重了学生的思维发展特点，也使学生充分认识到线段图这一几何直观模型对自身数学学习的重要价值，能将抽象的文字语言转译为直观的线段符号，从而直观洞察线段图所表征的数量关系，使线段图成为学生解决抽象、复杂的数学问题的脚手架，同时有效地发展学生的几何直观素养。

（三）活用面积图模型，培养学生的几何直观

线段图模型在解决问题中的重要作用已得到大家的共识，然而有些时候则需要借助面积图模型。尤其是在对算理的推理过程中，面积图模型有着独特的作用，能将一些抽象的算理进行直观的表征，促进算理从内隐走向外显，让算理可视化[5]。

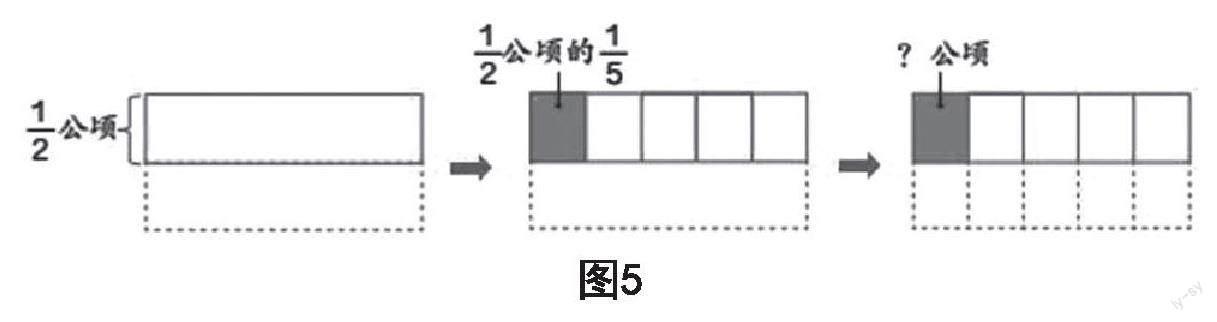
例如，在讲授人教版数学六年级（上册）“分数乘法”这一内容时，学生对“×”的算理常常无法理解，

而教材能立足于学生的现实思维困点，运用画面积图的

方式让学生正确理解（如图5）。第一幅图画出1公顷的一半，表示公顷，第二幅圖将公顷看作一个整体，

平均分成5份，其中的一份就是表示“公顷的”，也就是“1公顷的”，得出答案为公顷。紧接着，教材又呈现“×”。这时，教师就可以放手让学生画面积图表征算理。事实表明，运用面积图几何模型，能成功地将抽象的算理直观化，让每个抽象的数字都能表征它对应的意义，让学生直观感悟出数学运算算理的可视化，不但掌握算法，而且理解算理，更有效地发展几何直观素养。

三、结束语

对学生几何直观素养的培养是一个漫长的、往复的过程，并非朝夕之事。几何直观素养作为一项重要的核心素养，应引起所有小学数学教师的重视。教师应在具体课堂实施过程中根据教学内容的实际与学生思维的内需，通过创设情境、画图、构建直观模型等多种路径激发学生的直观感知，引发学生的直观体验，启发学生进行直观洞察，从而促进学生的数学思维顺利进阶，有效地培养学生的几何直观素养，为学生的学习和发展奠定基础。

参考文献

[1] 魏雯.让“线段图”活起来：以“和倍问题”教学为例[J].小学教学参考，2022（14）：64-66.

[2] 陈秀华.经历活动 积累经验：以“平行四边形的面积”为例[J].基础教育研究，2015（24）：41-42.

[3] 王桂先.小学数学几何的教学策略[J].教书育人（校长参考），2016（2）：74.

[4] 吉芸.小学数学“图形与几何”教学中的德育元素及其渗透[J].小学教学研究（理论版），2018（5）：21-22.

[5] 施雁飞.小学数学教学如何培养学生核心素养[J].中小学教学研究，2018（11）：82-85.

作者简介：许剑钬（1984.2-），男，福建莆田人，

任教于福建省莆田市城厢区灵川下尾小学，一级教师。