基于降维理念与无量纲解法的落石冲击力推导

2024-01-05王星霰建平王永东叶飞黄帅

科学技术与工程 2023年34期

王星, 霰建平, 王永东, 叶飞, 黄帅

(1.长安大学公路学院, 西安 710064; 2.中交第二公路工程局有限公司, 西安 710065;3.中交集团山区长大桥隧建设技术研发中心, 西安 710199)

隧道洞口及道路高边坡处危岩落石灾害常有发生,防护结构准确设计的核心即是准确解析落石最大冲击力,落石冲击力计算现已成为中外学者竞相研究的热点课题。

文献[1]依托模型实验提出一种落石冲击力的半理论半经验的计算方法。文献[2]通过现场实验及动量定理提出一种落石冲击力计算方法。日本道路公团亦提出一种落石冲击力半理论半经验计算方法[3]。文献[4]基于接触理论建立了落石最大冲击力估算模型。文献[5]依托实验研究落石质量、坡面坡度等相关参数对落石跳动范围影响。文献[6]研究分析印度Sutlej河流沿线交通走廊落石稳定性。文献[7]通过采用CADMA软件预测模拟了落石冲击特性及轨迹预测。

《公路隧道设计细则》[8]与《铁路隧道设计手册·隧道》[9]基于动量定理给出了一种落石冲击力算法。文献[10]采用理论计算及数值模拟方法,推导了落石冲击力的弹塑性算法解。文献[11]计算通过Hertz理论及JKR理论探究了落石最大冲击力的计算方法。文献[12]采用正交试验探究了落石下落高度及垫层倾角等若干因素对落石冲击力的影响效果。文献[13]通过试验及无量纲方法提出了一种落石最大冲击力计算方法。文献[14]通过落石冲击棚洞模型试验提出了一种落石冲击力计算方法。文献[15]采用室内落石冲击试验得出落石冲击冲击力与速度呈幂指数相关。文献[16]采用室内模型试验测试及数学归纳方法提出了一种落石冲击力计算方法。文献[17]采用理论及数值模拟方法,归纳一种落石冲击力计算方法。文献[18]结合数值计算与数学拟合算法,归纳出落石冲击输电塔结构的峰值冲击力计算公式。文献[19]基于Hertz弹性理论及Thornton弹塑性理论,提出一种落石最大冲击力计算方法。文献[20]通过3D打印方法构建5种椭球体,并联合室内模型试验推求出与形状系数相关的落石冲击力计算公式。

关于落石最大冲击力算法研究,已有研究成果意义重大,然基于力学及数学视角探究落石冲击力的研究成果仍略有欠缺,为此,现结合多因子降维(multifactor dimensionality reduction,MDR)降维理论推导落石最大冲击力计算公式;基于杨其新算法探究其三角形与正弦积分修正算法;采用LS-DYNA软件模拟落石冲击工况,归纳杨其新算法扩大系数规律;联合室内模型试验及无量纲理论,提出一种落石冲击力无量纲算法。希冀为落石冲击力研究与防护结构设计提供借鉴与参考。

1 冲击力代表性算法

(1)瑞士算法[2]。

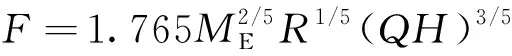
(1)

式(1)中:F为冲击力,N;ME为缓冲垫层弹性模量,Pa;R为落石等效球体半径,m;Q为落石重量,N;H为下落高度,m。

(2)日本算法[3]。

F=2.108(Mg)2/3λ2/5H3/5

(2)

式(2)中:M为落石质量,kg;g为重力加速度;λ为拉梅常数,建议取1 000 kN/m2。

(3)隧道手册算法[9]。

(3)

(4)

(5)

式中:V为冲击垫层瞬时初始速度,m/s;T为冲击持续时间,s;h为垫层厚度,m;c为冲击压缩波传播速度,m/s;ρ为垫层密度,kg/m3;E为垫层弹性模量,Pa;υ为垫层材料泊松比。

(4)杨其新算法[14]。

(6)

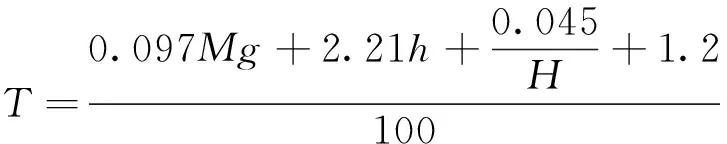
(7)

式中:a为落石冲击加速度,m/s2。

2 MDR降维理论推导计算

落石侵彻下部垫层土体后,球体与垫层间形成球冠接触。结合多因子降维理念 (multifactor dimensionality reduction,MDR),首先计算接触面某点冲击力,扩展该点至水平圆,根据微积分思想再扩展至该点所在水平圆环,通过自下而上积分,结合几何关系与能量守恒计算冲击力,计算模型如图1所示。

L为最大侵彻深度;xθ、yθ为触球冠上某点的横、纵坐标;θmax为过球冠底部水平线与垫层表面连线的夹角;θ为过球冠底部水平线与(xθ,yθ)点连线的夹角;ys(θ)为(xθ,yθ)处垫层压缩量;Fmax为落石最大冲击力;Z为竖轴;O为坐标原点图1 MDR理论模型Fig.1 MDR theoretical model

对于球心在x=0、y=R位置处的圆形,该圆在极坐标下的表达式为

ρ=2Rsinθ

(8)

式(8)中:ρ为极轴长度。

二维圆形与下部垫层平面所接触区域任意一点的坐标(xθ,yθ)可表示为

(9)

假定落球最大侵彻深度为L,接触球冠上某点(xθ,yθ)处垫层压缩量为ys(θ),则ys(θ)可表示为

ys(θ)=L-2Rsin2θ

(10)

侵彻深度值L可用落球底部与垫层上表面边缘最大夹角θmax为

L=2Rsin2θmax

(11)

联立式(10)和式(11),可得

ys(θ)=2R(sin2θmax-sin2θ)

(12)

此时依据微元条分积分原理,可得落石最大冲击力Fmax表达式为

(13)

式(13)中:l为圆环高度;kF为下部垫层结构法向刚度,表达式为

(14)

联立式(9)～式(14)可得

(15)

对式(15)进行积分计算后,可得

(16)

落石侵彻垫层后的能量耗散Wd可表示为

(17)

则有

(18)

对式(18)进行积分后可得

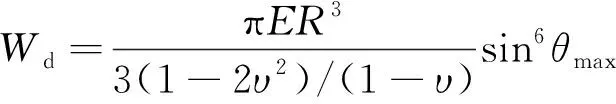
(19)

根据能量守恒原理,则有

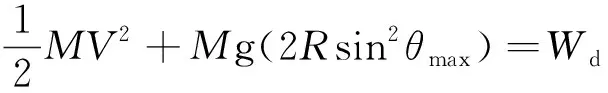
(20)

联立式(19)和式(20),通过给定初始冲击速度V,即可求得θmax、L、Fmax值。

3 理论与数值计算修正

3.1 最大冲击力分析

落石冲击坡面动力过程如图2所示。假定冲击坡面前速度矢量为Vc,沿平行、垂直于坡面依次分解为vq1与vf1,冲击回弹后落石速度矢量为Vt并分解为vq2与vf2,落球冲击坡体持续时间为T,坡体倾角为β,f(t)为冲击力随时间变量。

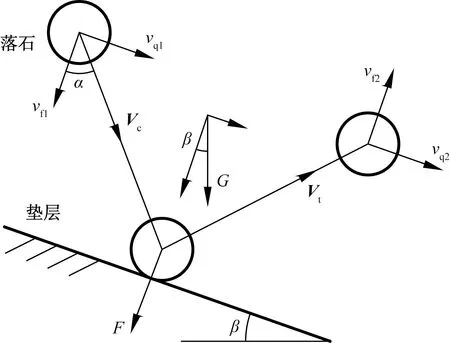
G为落石重力;F为落石冲击力;α为落石冲击入射速度与坡面法向的夹角图2 落石侵彻坡面Fig.2 Rockfall penetratingslope

考虑重力因素对落石冲击力影响,若重力冲量为IG,则有

IG=Mgcosβ×T

(21)

根据冲量定理,则有

(22)

ξn为落石冲击坡面土体的法向回弹系数,按式(23)计算,具体取值参考文献[16]。

(23)

(24)

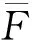
联立式(21)～式(24),落石冲击力修正算式为

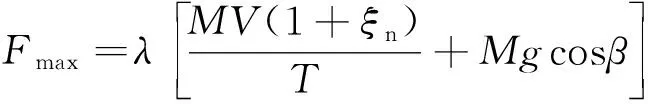
(25)

落石以自由落体运动形式冲击坡面时,其最大冲击力修正算法为

(26)

3.2 冲击力扩大系数推算

3.2.1 三角形修正算法

据Azzoni冲击力模型,可将落石冲击力曲线近似为等腰三角形,据冲量守恒原则,矩形面积SJ与三角形面积SS相等(图3),则有

图3 三角形修正Fig.3 Triangle correction

(27)

落石最大冲击力的三角修正算法为

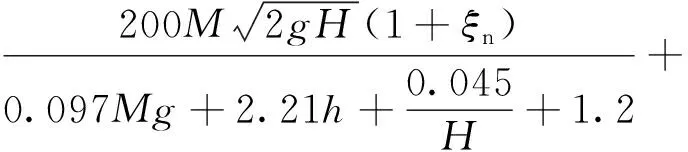
(28)

3.2.2 三角函数修正

采用正弦曲线模拟冲击力曲线。据冲量守恒定律,平均冲击力冲量与实际冲击力形成的冲量相等(图4),则有

图4 正弦修正Fig.4 Sine correction

(29)

由于f(t)满足正弦变化规律,则有

f(t)=Fmaxsin(ωt)

(30)

正弦曲线存在等式为

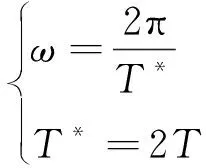
(31)

式(31)中:ω为正弦曲线角速度;t为时间;T*为正弦曲线周期。

联立式(29)～式(31),可得

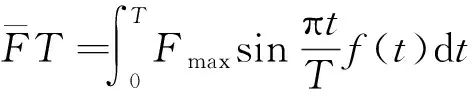
(32)

化简后则有

(33)

即落石最大冲击力的正弦修正算法为

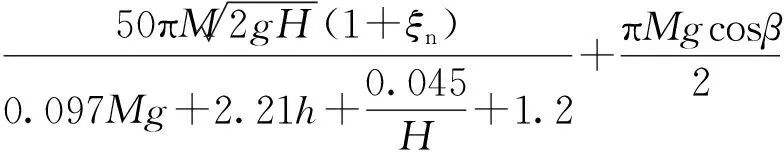
(34)

3.2.3 落石最大冲击力数值计算

构建落石冲击垫层的动力计算模型,寻求冲击速度与扩大系数相关关系。采用LS-DYNA动力显式计算软件,垫层尺寸为长×宽×高=6.0 m×6.0 m×2.5 m,落石半径取0.4、0.6、0.8、1.0 m,下落高度取5、10、15、20、25 m,对应冲击速度为9.899、14.000、17.146、19.799、22.136、24.249 m/s。落石采用Rigid刚性模型,垫层土体采用Drucker-Prager弹塑性计算模型。落球与垫层间采用面-面接触,垫层底部设置全约束,垫层四周面设为无反射边界。冲击时间取为0.5 s,设置100计算步。落球为864个单元,垫层为90 000个单元。重力加速度取9.8 m/s2。计算模型如图5所示,计算参数如表1[16,21]所示。

表1 模型计算参数Table 1 Model calculation parameters

图5 数值计算模型Fig.5 Numerical calculation model

图6为落球半径0.6 m,下落高度为20 m时垫层内部应力云图。由图6可见,在落球瞬态冲击作用下,垫层内部即形成快速的应力响应状态,且有明显的应力集中趋势。随冲击时间推移,正下方应力范围逐步向外震荡扩散。

图6 垫层应力分布云图Fig.6 Cloud chart of cushion stress distribution

图7为落石半径1.0 m时加速度变化曲线。由图7可见,各计算工况下加速度曲线呈同频变化趋势,各曲线整体满足脉冲式变化规律。随落球冲击高度增大,加速度峰值逐步增加,而峰值加速度时间则逐步缩短。当下落高度由5 m增加至25 m时,加速度峰值依次为190.313、224.997、254.100、262.070、268.581 m/s2,即下落高度增至一定程度后,加速度峰值基本呈平稳状态。各计算工况下落球加速度如表2所示。

表2 冲击力模拟值及扩大系数Table 2 Impact force simulation value and expansion coefficient

图7 加速度数值计算曲线Fig.7 Acceleration numerical calculation curve

根据表2的数值计算统计数据,绘制落石冲击速度与扩大系数散点图,如图8所示。由图8可知,针对不同落石半径,冲击力扩大系数拟合曲线变化规律基本类似,随冲击速度增加,扩大系数逐步缓和。采用指数函数进行曲线拟合,可得出4种落石半径下的λ-V关系式为

图8 速度-冲击力扩大系数拟合关系Fig.8 Fitting relationship between velocity impact force amplification coefficient

(35)

综合考虑式(35)所给4种λ-V关系,确定以式(36)表征冲击速度V与扩大系数λ关系。

λ=9.756V-0.499 54

(36)

联立式(26)和式(36),求得落石最大冲击力的数值计算修正算式为

(37)

4 最大冲击力量纲分析法

4.1 冲击力量纲分析

针对影响落石最大冲击力的4项因素构建落石冲击力的无量纲算法公式,包括落石质量M、垫层弹性模量E、垫层厚度h、冲击速度V、速度与坡面法向夹角为α。

关于落石冲击速度,文献[13]结合试验数据得出冲击力F与V4/3成正相关,文献[15]通过试验得出F与V1.85成正相关。隧道手册算法基于动量定理得出F=MV/t,表明冲击力与速度1次方成正相关。杨其新算法基本采用动量定理表达式,其冲击持续时间受下落高度影响,通过代入实际工况参数,0.045/H变量基本对冲击持续影响可近似忽略,即冲击力基本与速度1次方成正相关。日本和瑞士算法均表明冲击力与下落高速H3/5相关,亦即与V6/5成正相关。

针对落石质量参数M,文献[13]与日本算法均表明冲击力F与M2/3相关,国内算法均表明F与M的1次方相关。日本公式表明F与拉梅系数λ2/5相关,根据式(1)得F与E2/5相关。隧道手册算法表明F与时间T成反比,而T与E1/2成反比,即F与E1/2成正比。文献[13]表明F与E1/3相关。

隧道手册算法表明冲击力F与垫层厚度h呈正相关,存在一定准确性。日本算法、瑞士算法均未考虑参数h影响。此处参考杨其新室内试验研究数据[14],拟合h-F关系(图9),归纳出F与h-0.25相关,可见随垫层厚度逐步增加,h值对冲击力影响逐步减小。

图9 h-F拟合关系Fig.9 h-F fitting relationship

基于上述分析提出一种落石冲击计算无量纲表达式为

F=CM2/3E2/5h-1/4(Vcosα)3/2

(38)

为了待定系数C,并验证式(38)的可靠性,本文研究设计一套室内模型试验系统。

4.2 试验验证

采用自主设计的落石冲击棚洞结构相似模型试验装置,装置包括3个系统:门框式落球起吊系统、框架式棚洞系统、数据采集系统,如图10所示。

比例尺为1∶10图10 几何相似室内模型试验Fig.10 Geometric similarity indoor model test

试验参照一定几何相似比CS展开研究,模型试验遵循的相似原则[21]为

CE=Cσ=Cε=1

(39)

式(39)中:CE、Cσ、Cε分别为弹性模量、应力、应变相似比。

模型试验遵循的能量相似比CN为

(40)

式(40)中:JS、JM为实际与模型试验冲击能量。

根据Muraishi等[22]统计记载日本某铁路干线在1987-1997年间的落石情况调查,发现落石冲击能量小于1 000 kJ的落石工况占90%以上。结合上述分析,本文拟定模型试验相似比为1∶10,由此通过模型试验中100 J能量模拟实际工况1 000 kJ能量。

铁球密度7 859 kg/m3,质量为5.52 kg,顶板采用C30混凝土模筑而成,长×宽×厚=130 cm×49 cm×4 cm。顶板两侧采用钢化玻璃防护。加速度计固接于落球正上方,采用日本TMR-381型动态信号采集仪,图10所示。针对不同下落高度、垫层厚度开展试验,下落高度取1.0、0.8、0.6、0.4 m,砂土垫层厚度取12、10、8、6 cm,冲击力测试结果如表3所示。

表3 冲击力实测值与计算值Table 3 Measured and calculated values of impact force

据式(38)及试验值,令χ=M2/3E2/5h-1/4×(Vcosα)3/2,将F-χ关系绘制散点图,如图11所示。判断冲击力系数C靠近值0.136,确定式(41)为冲击力最终算式。再次采用式(41)计算落石冲击力,通过对比试验测试值,验证了该式具备一定可靠性。

图11 量纲法系数拟合Fig.11 Dimensional method coefficient fitting

F=0.136M2/3E2/5h-1/4(Vcosα)3/2

(41)

5 算例验证

5.1 依托工程冲击力对比计算

西宁至成都铁路群科隧道洞口工程,自然坡度为60°～70°,局部基岩出露,为晚二叠系西马组板岩夹变质砂岩夹灰岩,洞口上方山体高陡,基岩裸露,岩石凸起,岩质较坚硬,发育多组节理,岩块易沿节里面崩落,危岩、落石发育。陡坡上岩块易沿节理崩落,属于不稳定岩体,存在危岩、落石隐患,部分落石滚落方向朝向洞口,对隧道洞口及桥墩直接构成威胁,隧道出口斜坡下部堆积大量块石及碎石,一般粒径为0.4～2.0 m。现场考虑以洞口上方粒径1.6 m落石作为控制灾害工况,冲击速度极限值按24 m/s考虑,落石密度按2 450 kg/m3考虑,对应冲击能量为1 512.505 kJ,考虑8、12、16、20、24 m/s计算工况,垫层计算参数参照表2,计算落石最大冲击力,为防护结构设计提供参考。

图12为针对控制性落石在各冲击能量情况下最大冲击力计算结果。由图12可见,MDR理论算法、三角形修正算法、正弦修正算法、数值模拟算法以及无量纲算法结果整体具备一定的吻合性。相较而言,瑞士、日本算法结果适度偏高,这或可能由于二者在计算时均未考虑垫层参数影响所致。杨其新算法结果整体相对偏低,这是由于该算法是计算整个冲击时间内的冲击力,所得冲击力并非冲击力峰值。垫层材料对落石冲击力影响较大,碎石土垫层情况冲击力最高,砂土垫层次之,黏土垫层最小。冲击能量越小,各算法结果吻合度愈高。在砂土垫层情况下,冲击速度为24 m/s时,瑞士、日本算法值依次为6.12、5.57 MN,本文所给5种算法值维持在2.21～3.45 MN,约为瑞士算法1/2,为日本算法的2/3。以下再采用野外实际冲击灾害验证本研究算法。

图12 落石冲击力对比计算Fig.12 Comparison and calculation of rockfall impact force

5.2 Pichler野外落石冲击验证

为探究落石最大冲击力,Pichler进行了野外巨石冲击试验,试验落石质量为10 160 kg,等效直径d=1.63 m,冲击速度为6.26 m/s(工况1)、12.95 m/s(工况2)。再采用18 260 kg落石,等效直径1.99 m,冲击速度为13.00 m/s(工况3)、19.14 m/s(工况4)、19.23 m/s(工况5)。现场采用分层压实砂土垫层,尺寸为长×宽×高=25 m×4 m×2 m,密度为1 800 kg/m3,紧砂垫层弹模取67 MPa。泊松比为0.17。现针对上述试验进行对比计算。

表4为Pichler试验与本文各算法结果对比情况,图13为相应统计图。由图13可见,瑞士算法、隧道手册算法结果适度偏高,本文研究中各算法结果与Pichler试验结果吻合度较好,特别是MDR算法、无量纲算法、日本算法结果均与Pichler试验结果高度吻合,验证本文算法具备一定可靠性。

表4 Pichler试验工况各算法解Table 4 Algorithm solutions of pichler test condition

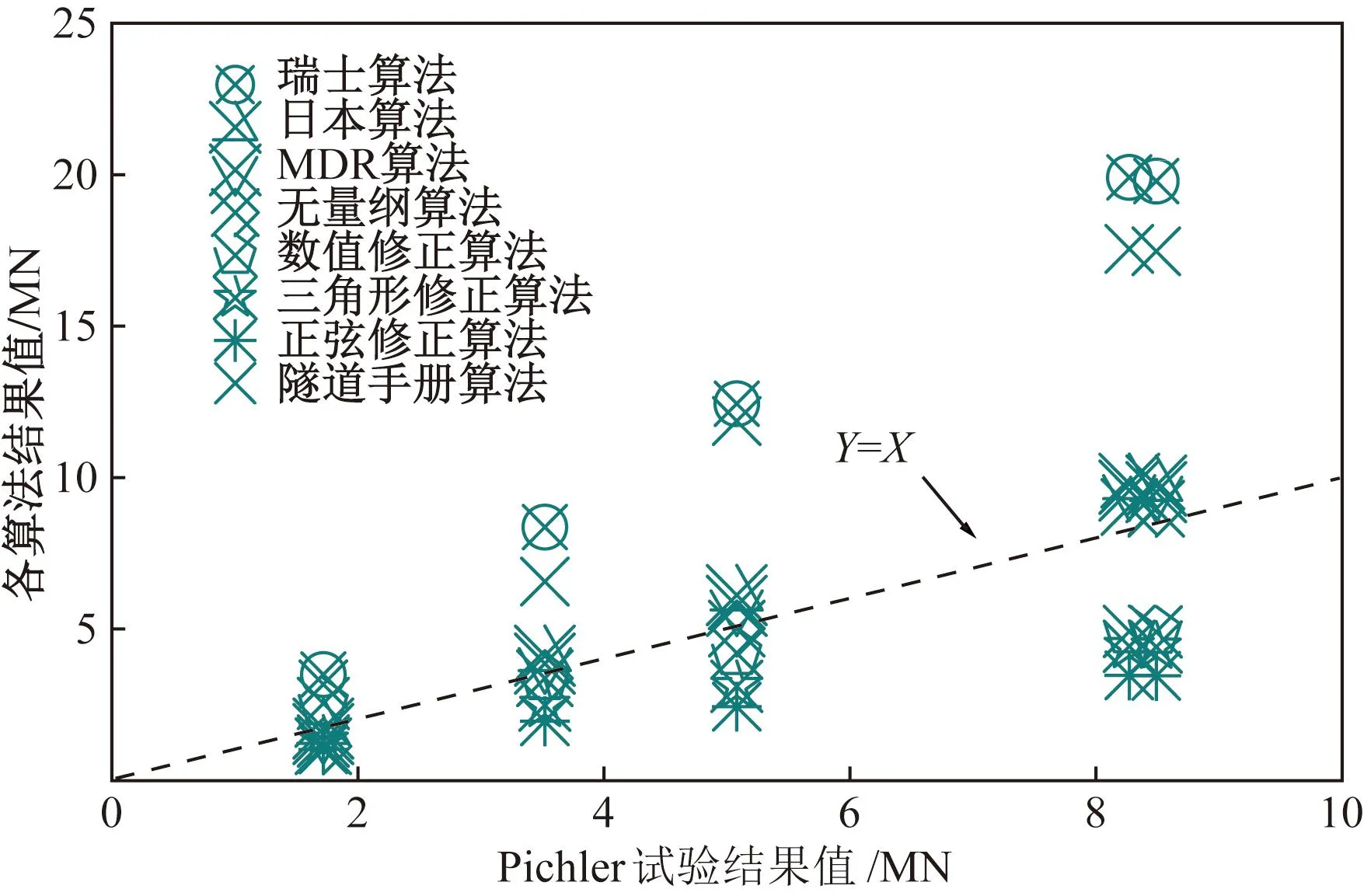
图13 Pichler试验结果-各算法解对比Fig.13 Pichler test results-comparison of solutions of each algorithm

5.3 彻底关大桥野外冲击灾害验证

彻底关大桥位于四川省汶川县境内,为国内最长拼装钢架桥。2009年7月5日05:00左右,连续降雨导致桥墩附近坡体产生崩塌,巨石冲击下部桥墩后致桥面垮塌。经事故调查:撞击巨石质量为M=148 000 kg,密度ρ=2 850 kg/m3,冲击速度V=11.5 m/s,落石弹性模量为83×109Pa,桥墩弹性模量为20×109Pa,桥墩厚度为1.5 m,桥墩抗折断强度为25 MN[13]。

将上述参数代入式(41)进行计算,解得最大冲击力的无量纲算法值为174.5 MN。通过式(16)解得冲击力得MDR算法值为132.5 MN,可见两算法结果较接近,且以该冲击力可轻易摧毁桥墩结构,验证本文算法可在野外环境进行计算应用。