基于量纲分析法的动能弹侵彻深度计算公式

2024-01-05戴银所

弹道学报 2023年4期

戴银所

(陆军工程大学国防工程学院,江苏南京 210007)

动能弹侵彻研究多集中在中低速范围,相关实验研究及经验公式、理论模型和数值模拟等已初成体系[1,2]。目前各国防护手册中侵彻深度的计算公式大都拟合自实验数据,其形式不同,各自适用范围和条件也有差别,具有简便、实用、在其适用范围内准确性高等优点,但也存在适用条件有限、局限性较大的缺点[3-5]。

量纲分析法又称因次分析法,以量纲齐次方程为理论基础,其优点是可以不局限于已知微分方程的物理现象,尤其适合分析机理尚未知、规律尚未掌握的复杂现象[6-8]。量纲分析法有助于确定关键控制因素,弄清蕴含在实验结果中的本质性规律。虽然量纲分析法在控制因素选择上具有一定主观性和假定性,但最终都需要得到尽可能多实验验证[9,10]。

本文基于能量守恒和转化定律以及动能原理,采用量纲分析法,依托布氏硬度计算公式,推导动能弹侵彻深度计算公式,并提出侵彻效率和侵彻效率系数的概念。分别选取动能弹中低速侵彻岩石、金属和混凝土的文献数据,计算侵彻效率系数和侵彻效率,通过评价侵彻效率与速度之间的相关性,判定动能弹侵彻深度计算公式的合理性。

1 侵彻深度计算公式推导

根据各类经典理论和大量研究可知,弹体在侵彻过程中,对侵彻破坏效果产生影响的因素有:弹体的速度、质量、尺寸、密度、强度、弹性模量,靶体的强度、内摩擦角,以及弹靶之间摩擦等[11]。

靶体特征阻力反映靶体材料抵抗侵彻的固有能力,但不同文献的取值方法不同,一般采用靶体材料的单轴抗压强度[12],其表示单位面积所受到的力。而动能弹侵彻可以认为是以球面点开始受力的一种局部作用[13],所以用材料硬度表征材料抗侵彻的能力更准确[14,15]。从细观尺度上来说,岩石和混凝土是非均质材料、各向异性,表面测出的硬度值不能表征材料内部的真实硬度,因此没有硬度指标。但它们的硬度与抗压强度正相关,故可以借助抗压强度来描述其抗侵彻能力[16,17]。推导过程如下:

①确定函数表达式。

侵彻破坏效果以侵彻深度h表示,与弹体材料密度ρ、弹性模量E、质量m、速度v、弹径尺寸d,以及靶体的硬度H、容重γ、泊松比μ、内摩擦角φ之间关系可表达为:

f(m,v,d,ρ,E,H,h,γ,μ,φ)=0

(1)

②确定主要影响因素。

动能弹侵彻试验一般用金属弹丸模拟动能武器。考虑到试验弹丸使用的合金钢与动能武器材料基本一致,故弹体的材料性能参数如E、ρ皆认为为常数,即相似比为1;φ和μ是无量纲物理量;对于岩石、金属、混凝土靶体,容重相似比易于实现为1。因此,为了降低运算难度和运算量,认为弹体的E、ρ,靶体材料的γ、μ、φ等参数是常数,确定影响侵彻效果的主要因素是m、v、d、H,从而建立如下关于侵彻深度的函数表达式:

f(m,v,d,H,h)=0

(2)

③写出因次式。

采用量纲分析法建立常数K的因次式:

K=mavbdcHehg

(3)

式中:a、b、c、e、g都是不为0的整数。

④解出因次式的一般式。

常用物理量的量纲如表1所示,将其带入式(3),得:

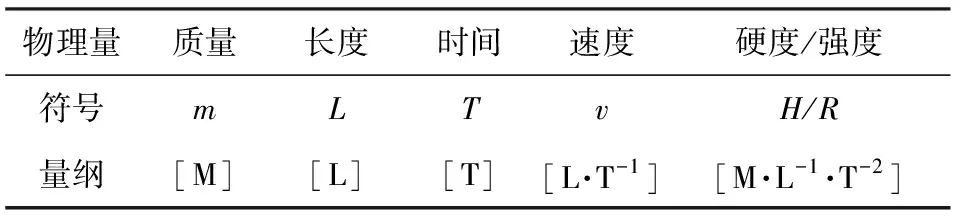
表1 常用物理量的量纲Table 1 Dimensions of common physical quantities

K=[M]a[L]b[T]-b[L]c[M]e[L]-e[T]-2e[L]g

(4)

量纲合并得:

K=[M]a+e[L]b+c-e+g[T]-b-2e

(5)

由于K为常数,等式为无量纲,所以有:

(6)

由于a、b、c、e、g都是不为0的整数,故可以令a=1,解得e=-1、b=2。即:

2+c+1+g=0

(7)

由此,可以得到两组最简单解:

进而可以建立2个一般式,分别是:

(8)

(9)

硬度是描述材料局部抵抗硬物压入其表面的能力,其中布氏硬度HB采用一定直径(1～10 mm)淬硬钢球压入材料表面测量,这与动能弹弹头侵彻材料过程基本相似。根据布氏硬度计算公式可知,当钢球压入材料深度超过半径时,硬度计算式为[18]:

(10)

式中:F为侵入压力,A为受力面积(对于球体来说就是球冠的面积),d为钢球直径。

钢球侵入压力对材料所做的功等于侵入压力侵彻深度的积,当弹体静止时侵彻压力为零,故平均侵彻压力取F/2。

则侵彻压力做功:

EF=h×F/2=πd2hHB/4

(11)

为了与式(8)和式(9)中的硬度H一致,上式改写为:

EF=πd2hH/4

(12)

因此,式(9)分母具有动能弹压力做功的物理意义。将式(12)代入式(9)得:

(13)

式(13)继续变形,得:

(14)

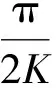
式(9)可以变形为弹体侵彻深度的表达式:

(15)

式中:侵彻效率系数K包含了弹体材料性能、弹头性状、长径比、侵入角度等因素。

2 文献实验数据验算

岩石、金属、混凝土是3类最常使用的防护材料,本节利用推导的侵彻深度计算公式对半球形或近半球形弹体的多组文献试验数据进行侵彻效率计算,并对计算结果的有效性进行评价。

2.1 侵彻岩石

由于岩石是脆性材料,难以采用布氏硬度试验方法测量其布氏硬度,一般用坚固性系数来表示岩石抵抗外力破坏的能力,即普氏硬度系数,其值为岩石标准试样的单向极限抗压强度值的十分之一。用该值来描述岩石破碎抗力具有足够高的准确性和稳定性[20,21]。

①第一组:对文献[22]开展的岩石侵彻深度实验数据进行侵彻效率系数和侵彻效率计算,已知其弹头系数CRH为3,计算结果如表2所示。由于速度超过900 m/s时弹体出现了严重失稳,发生跳弹,故本文仅对速度不超过900 m/s的数据进行计算。

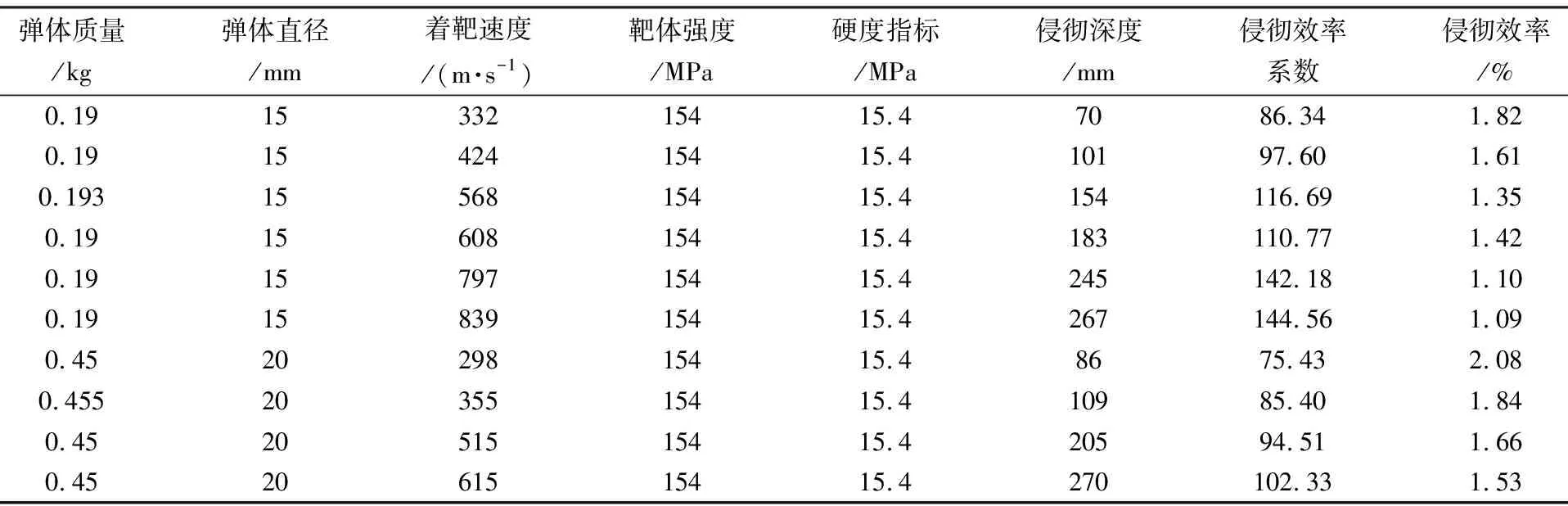
表2 文献[22]侵彻效率计算Table 2 Calculated penetration efficiency of reference [22]

从表2可以看到:速度在332～839 m/s范围时,侵彻效率系数在75.43～144.56范围内,侵彻效率约为1.35%～2.08%;在相同弹体参数的情况下,侵彻效率随速度的增加而逐渐降低。

不区分弹径,将表2中所有的速度与侵彻效率进行拟合得:K=-0.001 6v+2.424 3,拟合公式的可决系数R2=0.913,说明侵彻效率与弹丸速度之间具有很好的负相关关系。

区分15 mm、20 mm两种不同弹径,分别进行拟合,则结果为:

(16)

两种弹径拟合公式的可决系数R2分别为0.965 9和0.930 9,都大于不区分弹径的可决系数,即表明同一种参数的弹进行侵彻试验,侵彻效率与弹丸速度之间的负相关性会更好。这两种不同规格弹体侵彻效率与速度之间拟合公式的一致性非常好,两个拟合公式的系数离散性很小,说明本文推导出的动能弹侵彻深度计算公式具有合理性。

②第二组:对文献[23]中模型弹在岩石介质中成坑效应试验数据进行分析,已知其弹头系数CRH为3,计算结果如表3所示。

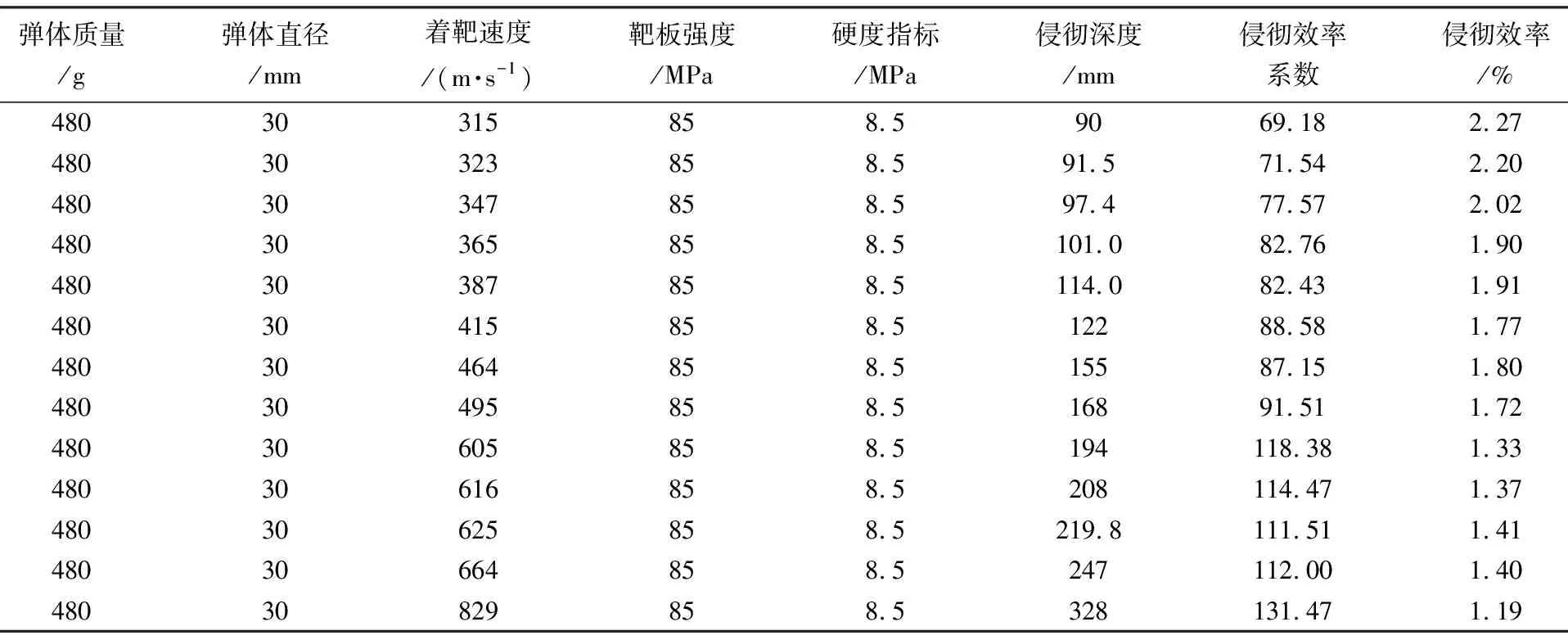
表3 文献[23]侵彻效率计算Table 3 Calculated penetration efficiency of reference [23]

从表3可以看到:速度在315～829 m/s时,计算出侵彻效率系数在69.18～131.47范围内,侵彻效率约为1.19%～2.27%,在相同弹体参数的情况下,侵彻效率随速度增加而逐渐降低。

将速度与侵彻效率进行拟合得:K=-0.002 1v+2.749 1,可决系数R2=0.907 7,说明侵彻效率与弹丸速度之间有很好的负相关关系。

文献[22]和[23]采用不同规格弹丸和靶体进行侵彻岩石试验,侵彻效率与速度拟合公式的系数离散性也很小。

2.2 侵彻金属

金属材料的硬度与强度一般存在正比例关系,抗拉强度一般约为布氏硬度的3倍[24],如碳素钢的抗拉强度为其布氏硬度的3.5～3.6倍。

文献[25]中试验靶板使用4340钢(其布氏硬度在280～320 MPa范围,本文取300 MPa),弹体外径为7 mm,弹头形状均为半球头(弹头系数CRH为0.5)的实验数据进行分析,结果如表4所示。靶板使用6061-T651铝合金(布氏硬度约100 MPa),弹体外径为7 mm,分别选用弹头形状为半球头(弹头系数CRH为0.5)和截卵头(弹头系数CRH为3)的实验数据进行分析,结果如表5所示。由于速度超过3 200 m/s时弹体在自由飞行过程中出现显著的弯曲现象,或侵彻过程中出现明显断裂,故选取速度在3 000 m/s以内的数据,并剔除击穿靶体的试样。

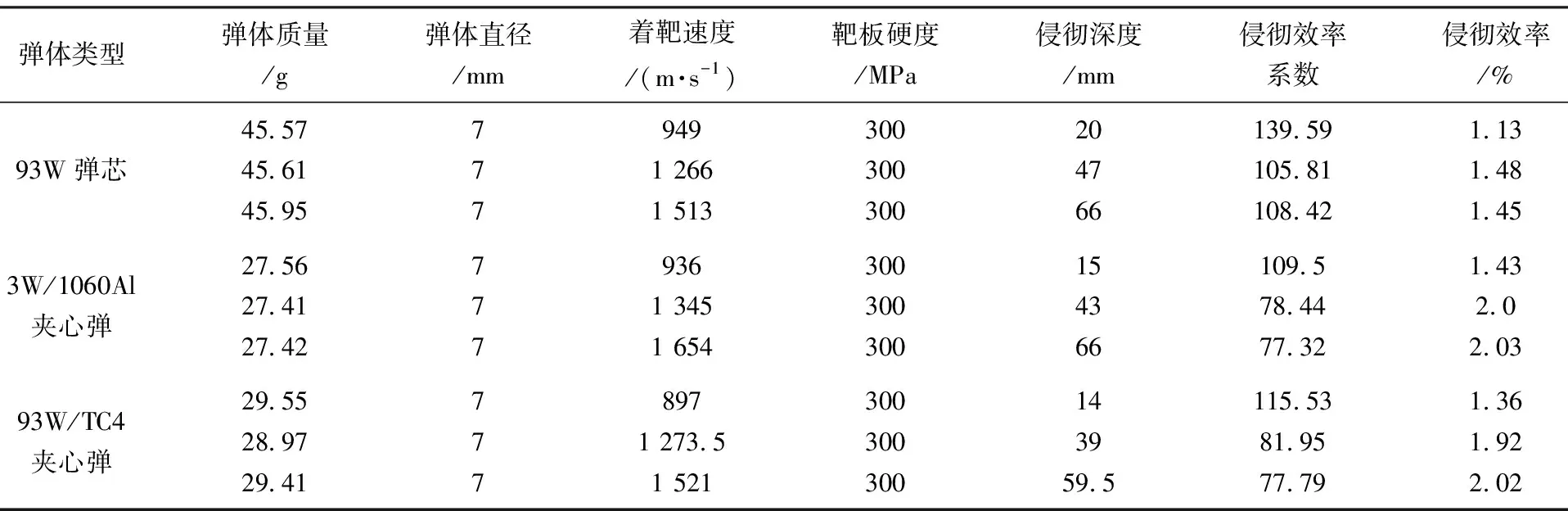
表4 文献[25]4340钢靶侵彻效率计算Table 4 Calculated penetration efficiency into 4340 steel target of reference [25]

表5 文献[25]6061-T651铝靶侵彻效率计算Table 5 Calculated penetration efficiency into 6061-T651 aluminum target of reference [25]

表4可以看到:侵彻效率系数在77.32～139.59范围,侵彻效率约为1.13%～2.03%;在相同弹体参数情况下,侵彻效率随速度增加而逐渐增加。针对三种弹径相同、质量不等的弹丸所有试验数据进行拟合得:K=0.000 9v+0.509 3,R2=0.538 4;对弹径相同、质量也相近的第2、3组数据进行拟合,得:K=0.001v+0.576 9,R2=0.879 7,相关性更好。

对三种不同的弹体分别进行拟合,93W弹芯数据的拟合结果为:K=0.000 6v+0.617 4,R2=0.744 9;3W/1060Al夹心弹数据的拟合结果为:K=0.000 9v+0.685 4,R2=0.849 1;93W/TC4夹心弹数据的拟合结果为:K=0.001 1v+0.421 8,R2=0.932。结果表面同一批试验中侵彻效率与弹丸速度之间有很好的正相关关系。

采用三种不同规格弹丸侵彻相同靶体时,侵彻效率与速度之间拟合公式的系数离散性也较小。

从表5可知:侵彻效率系数在32.92～222.34范围,侵彻效率约为0.71%～4.77%。当着靶速度大于2 000 m/s时,侵彻效率都小于1%。这是因为随着着靶速度增加,存在最大侵彻效率,这时候除了靶体抗压强度以外,弹体长径比、弹体材料强度及机械性能对侵彻效率的影响逐渐突显[26]。因此本文选用的侵彻岩石、混凝土文献其弹头着靶速度基本都在1 000 m/s以内。

将速度与侵彻效率进行拟合,半球头弹芯的数据拟合结果为:K=-0.001 3v+3.692 8,R2=0.857 1;截卵头弹芯数据的拟合结果为:K=-0.001 8v+4.914 2,R2=0.705 4。说明侵彻效率与速度之间有较好的负相关关系。这两组试验结果的拟合公式之间具有较好的一致性,拟合公式的系数离散性较低。

针对2组数据的拟合结果为:K=-0.001 6v+4.374 3,R2=0.707 3。说明其他参数都相同时,虽然截卵头侵彻效率稍大于半球头的侵彻效率,弹芯采用半球头和截卵头对中低速弹丸侵彻效果影响不明显。

2.3 侵彻混凝土

由于混凝土是非均质材料,没有硬度指标;但可以通过回弹法测试混凝土的抗压强度;其实回弹法测试得出的混凝土强度就是混凝土的布氏硬度,低强度时其值一般约为抗压强度的1.1倍[17,27,28]。

文献[10]开展了中长杆射弹侵彻混凝土实验,其弹头系数CRH为3;结合文献[9]可知:10 mm、20 mm弹试验时混凝土靶抗压强度值为16.5 MPa;40 mm弹试验时混凝土靶抗压强度值为30.0 MPa。20 mm弹,10 mm、40 mm弹侵彻混凝土的侵彻效率系数K、侵彻效率计算结果分别如表6和表7所示。

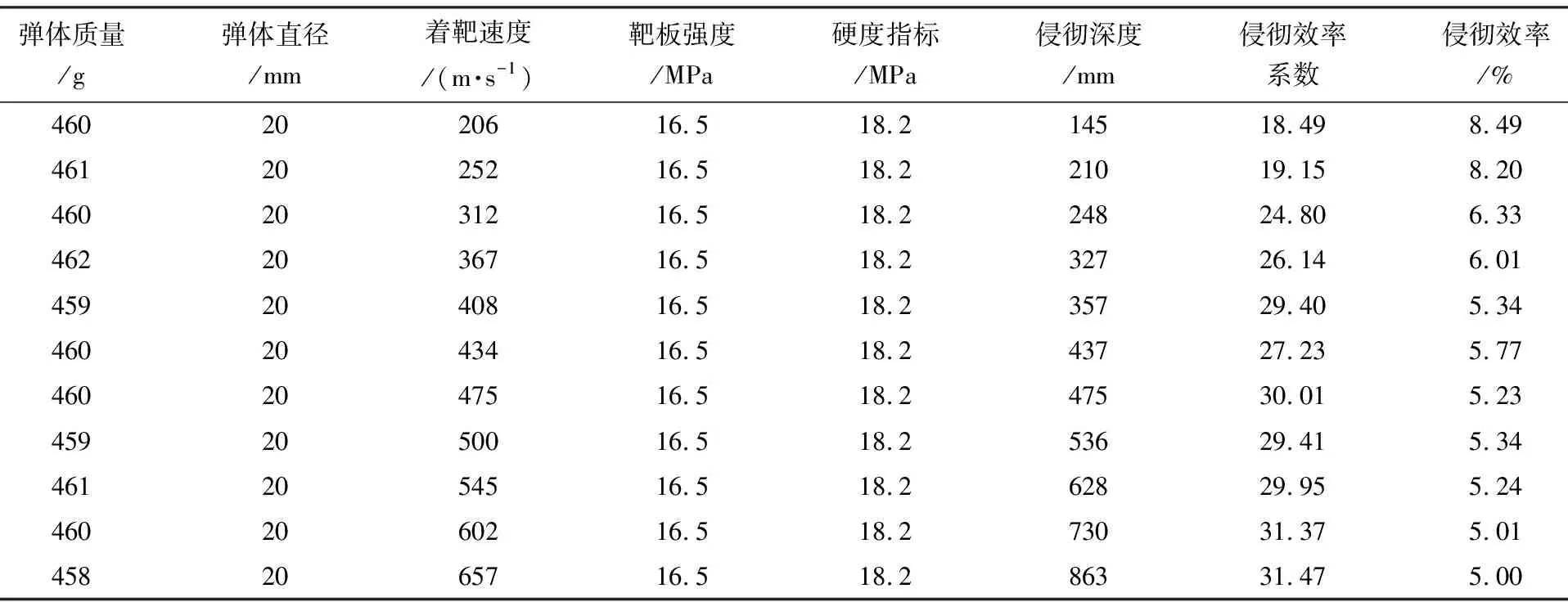
表6 文献[10]20 mm弹侵彻混凝土侵彻效率计算Table 6 Calculated penetration efficiency of 20 mm projectile into concrete of reference [10]

表7 文献[10]10 mm、40 mm弹侵彻混凝土侵彻效率计算Table 7 Calculated penetration efficiency of 10 mm,40 mm projectile into concrete of reference [10]

从表6可以看到:速度在206～657 m/s时,侵彻效率系数在18.49～31.47范围内;侵彻效率约为5.0%～8.49%。侵彻效率随速度增加而逐渐降低。对该数据进行拟合,得:K=-0.007 6+9.304 7,R2=0.774 1,这说明侵彻效率与速度之间有较好的负相关关系。

从表7可以看到:速度在330～831 m/s范围时,侵彻效率系数在12.08～34.99范围;侵彻效率约为4.49%～13.0%。同一种弹体,的侵彻效率随速度增加而逐渐降低。

对直径为10 mm的弹体侵彻混凝土数据进行拟合,结果为:K=-0.005 2v+7.961 6,R2=0.605 8(去除了弹体质量为56.5 g的数据);直径为40 mm的弹体侵彻混凝土数据拟合结果为:K=-0.009v+15.226,R2=0.982 5。说明侵彻效率与弹丸速度之间有较好的负相关关系。

不同弹体(10 mm和20 mm弹体)侵彻同一种靶体时,拟合公式系数离散性较低,变异系数为0.19。