某特殊结构枪弹气动外形与结构参数优化设计

2024-01-05展鹏遥常思江崔慧振

弹道学报 2023年4期

展鹏遥,常思江,崔慧振

(1.南京理工大学能源与动力工程学院,江苏南京210094;2.西北工业集团有限公司,陕西西安 710043)

枪弹作为一种小口径、高转速的无控弹丸,其射程、精度、对目标的作用效果等主要依赖于它的气动特性和结构特性,而气动特性又主要依赖于弹丸本身的气动外形和结构参数。对于常用的普通步机枪弹,其结构主要由弹头壳和弹心两部分组成。弹头壳的材料应具有一定强度和塑性,在膛内外运动时不产生过分形变,减小对膛线的磨损,常见的弹头壳材料为黄铜或铜合金。弹心材料出于成本和强度考虑多为钢或铅[1],如国产CS/DFL型7.62 mm高精度狙击弹采用铜被甲全铅心前装结构,美军5.56 mm M855枪弹采用铅钢复合心结构等。

目前,国内外针对各类弹箭的气动外形优化设计开展了大量研究。SKINNER等[2]对弹箭气动外形优化问题进行了综述,分析了常用优化方法的优点和局限性。王中原[3]针对低阻增程弹,在细长体理论下导出了最小波阻母线方程,同时研究了地炮榴弹[4]、脱壳穿甲弹[5]在不同约束、不同优化目标下的气动外形优化设计问题,均取得了良好的效果。在小口径枪弹弹道研究方面,GKRITZAPIS等[6]采用六自由度飞行动力学模型,对7.62 mm枪弹弹丸的受力情况、飞行轨迹和稳定性进行了详细的分析。SAILARANTA等[7]研究了7.62 mm子弹近乎垂直发射时弹道顶点的转弯现象,采用数值模拟的方法,重点分析了马格努斯力和力矩对子弹在弹道顶点姿态的影响。LAWHORN等[8]为提高弹道系数,采用液态金属技术设计了采用铅合金外壳和钢质穿甲心结构的5.56 mm枪弹,并对其穿甲能力进行了研究。熊镐[9]对枪弹气动力的工程算法和CFD仿真计算方法进行了对比,并构建了基于“标准弹”的气动力快速计算模型,据此研究了枪弹弹头部长度、弹尾部长度和船尾角对其气动特性的影响。李烨等[10]针对12.7 mm穿燃弹对钢靶板的侵彻行为进行了多发弹道试验和数值仿真,研究了侵彻深度、侵彻阻力与弹丸结构和着靶动能之间的关系,并在此基础上建立了弹芯刚性侵彻时的深度预测公式。

枪弹弹头作为一种实心金属弹丸,一般内部无装药、无引信,外部无其它弹身结构。制造枪弹所采用的材料、各材料用量、装配方式等对枪弹质量、重心位置、转动惯量等结构参数有所影响。这些结构参数又与气动外形共同影响枪弹的飞行过程。而目前考虑枪弹弹头结构参数对弹道特性影响的研究相对较少。LAHTI等[11]提出了一种通过设计内部质量分布方式来控制自旋稳定弹丸外弹道性能的方法,对不同任务需求的枪弹设计了不同的稳定性参数,以离散化弹丸内部质量的方式,获得了最佳的弹头质量分布。但这种将弹心离散为400个网格的方式,在目前实际生产中几乎无法实现,并且也未能与气动外形开展联合设计,故具有其局限性。

枪弹弹头内部质量分布对飞行稳定性有较大影响[11],本文从实际工程应用角度出发,以类似美国M855枪弹[12]的弹头结构为研究对象,提出一种同时考虑枪弹弹头气动外形与结构参数的设计方法,以3种材料的体积占比与诸气动外形参数为优化变量,在不改变枪弹弹头质量和初速的前提下,同时考虑弹丸外弹道性能与侵彻装甲能力,以抗横风风偏能力最强和穿甲厚度最大为优化目标,综合考虑外形、结构、稳定性等约束,建立了一个气动外形-结构参数多目标优化设计模型,采用标准粒子群算法寻求全局最优解。本文研究拟为枪弹外弹道设计提供一个新的思路。

1 弹道特性的影响因素分析

1.1 枪弹气动力计算方法

枪弹气动力计算是外弹道设计的基础,目前已有大量的气动力工程计算方法可供使用。在选取具体方法时应考虑尽量满足如下条件:

①有良好的计算精度和较快的计算速度;

②有较好的通用性,以适应对不同外形和结构的计算。

对此,本文选取了若干工程计算方法,如表1所示。

表1 气动力工程计算方法Table 1 Aerodynamic engineering calculation method

上述计算气动力的具体方法参见文献[13],根据表中所列方法已编制了软件可用于气动力计算。对一些已往弹形的计算结果表明,该方法的计算精度和速度作为旋转弹丸的气动力外形设计,使用效果较好。

1.2 气动外形参数对弹道特性的影响

枪弹设计的基本依据应由枪弹的战术技术要求来确定,其中精度是首要条件。影响精度的因素主要是弹丸的稳定性,对于高速旋转的弹丸,要求其满足陀螺稳定与动态稳定。两种稳定性的充分必要条件如下所示:

(1)

式中:Sg为陀螺稳定因子,Sd为动态稳定因子,具体计算公式见文献[14]。

由式(1)可知,陀螺稳定性是动态稳定性的必要条件,即动态稳定的弹丸始终是陀螺稳定的。如以Sd为横坐标,1/Sg为纵坐标,对于满足式(1)的稳定区域如图1中抛物线下方阴影部分所示,在抛物线内部的点都满足稳定性要求,故将此区域称为动态稳定域。

图1 弹丸动态稳定域示意图Fig.1 Dynamic stability region diagram of bullet

常规轻武器枪弹弹头外形结构如图2所示,主要由弧形部、圆柱部、尾锥部3部分组成。图3为3种不同全弹长细比的弹丸,在平射(射角为0.84°)条件下1 000 m射程范围内的稳定性情况。

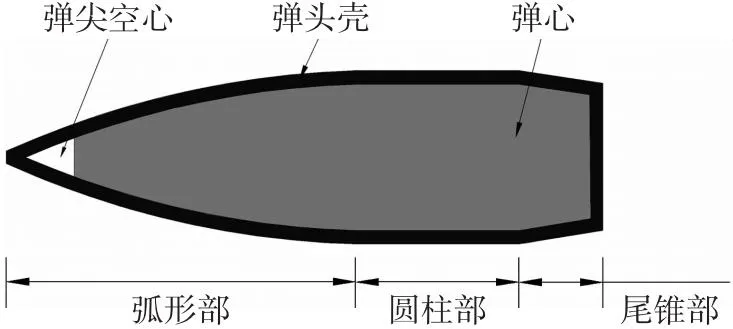
图2 枪弹弹头结构示意图Fig.2 Structure diagram of bullet warhead

图3 不同长细比弹丸飞行的稳定性情况Fig.3 Stability of projectile flight with different slenderness ratios

通常来讲,在一定范围内越细长的弹丸飞行时受到的空气阻力越小[15],在飞过相同射程时其所需飞行时间更短,落点威力更大。但由图3可见,大长细比的弹丸的稳定性更差,长细比λ=3的弹丸飞行全过程均在稳定域内;λ=4的弹丸在弹道末端才进入动态稳定域;λ=5的弹丸全弹道均不满足稳定性条件。因此,良好气动外形与稳定性的匹配成为外弹道设计中的重要问题和难点。

对3种弹丸的抗横风风偏能力进行分析,采用横风对侧偏的敏感因子α进行数学表征,即:

(2)

式中:Zw和Z0分别为有风和无风时的弹丸落点偏流,wz为横风速度。需要说明的是,该公式是一种估算,并不严格精确,但用于表征某种弹道性能,其误差可以接受,故外弹道学中常采用这种估算方式[16]。风偏敏感因子的计算过程为:每次计算两条弹道,一条不考虑横风(横风wz=0),得到落点偏流Z0,一条为存在横风情况(横风wz取为10 m/s)得到落点偏流Zw,代入式(2)即可求得α。在弹丸初速、转速、射程相同的情况下,α值越小,表示弹丸对横风的敏感性越小,抗横风的风偏能力越强。通过计算λ=3的弹丸,风偏敏感因子α=0.491 8;λ=4的弹丸,α=0.268 2;λ=5的弹丸,α=0.360 4。

3种弹丸中,λ=4的弹丸抗横风风偏能力最强。λ=3的弹丸虽然具有最好的稳定性,但其气动外形不佳,飞行时间长,抗风偏能力最弱。同理,λ=5气动外形虽然较好,但稳定性差,抗横风的风偏能力也较差。λ=4的弹丸稳定性与气动外形介于二者之间,具有最强的抗横风风偏能力。气动外形设计良好的弹丸在飞行中受到的阻力更小,在相同初速和射程条件下,落点速度更大,飞行时间也更短。此时,弹丸受横风影响的时长更短,在有横风情况下的偏流Zw更小,对准确命中目标更为有利。

1.3 结构参数对弹道特性的影响

1.3.1 结构参数的选取

本文选取的枪弹结构参数包括铜质弹头壳体积、铅心体积和钢心体积,同时也是本文弹头结构优化设计变量。对弹头结构做如下假设:

①弹头壳厚度均匀,呈完整包覆状态。

②弹心仅由铅钢2种材质填充,为双层结构。

③采用前装方式,在弹心前部可留有空心。

枪弹材质结构示意图如图4所示。

图4 枪弹弹头材质结构图Fig.4 Material structure diagram of bullet warhead

1.3.2 弹头结构特征量的计算

①弹头质量m。

弹头总质量由铜、铅、钢各自质量3部分组成(3者对应参数下标分别为t、q、g),当3者体积确定后,即可由各材料密度求得质量,即:

(3)

式中:Vi和ρi为各材料体积与密度。

②弹头的重心位置Xc。

弹头重心位置的计算公式可写为

(4)

式中:My,i为各材料对弹头顶端切面的重力矩,xi为各材料几何形体的形心至弹头顶端切面的距离。

③弹头的极转动惯量JC。

弹头的极转动惯量值为弹头壳、铅心及钢心极转动惯量的代数和,即:

(5)

式中:CΦ,i为各材质几何形体的体积极转动惯量,g为重力加速度。

④弹头的赤道转动惯量JA。

各简单几何形体的赤道转动惯量求出后,利用平行移轴定理,分别求出3种材质对赤道轴的转动惯量,求和后可得弹头赤道转动惯量,即:

(6)

式中:AΦ,i为各材质几何形体绕弹头赤道轴的体积转动惯量。

1.3.3 结构参数对弹道特性的影响

本节基于以上结构参数的计算方法对3种采用不同材料配比的弹头进行稳定性和风偏敏感因子的计算,弹丸外形参数和弹头壳厚度取为定值。通过调整铅心和钢心在弹心中的体积占比,计算弹丸结构参数,出于弹尖空心的限定,将铅心和钢心总体积定为弹心体积的90%。选取的3种弹丸结构参数如表2所示。

表2 弹丸结构参数Table 2 Structural parameters of projectile

由表3可知,弹A为全铅心弹丸,弹B与弹C为铅钢复合心弹丸。由于铅钢的密度不同造成弹丸质量分布不均,通过调整铅钢比例可使弹丸重心位置沿弹轴移动。计算结果显示弹B与弹C的重心位置均比弹A靠近弹头前端。对3者进行稳定性计算,结果如图5所示,弹A、B、C在飞行初始阶段均处于稳定域外,弹B与弹C在飞行后程进入了稳定域内,相比之下,弹A只有在弹道终点的很小一部分才满足稳定性条件,弹A的飞行稳定性整体要差于弹B与弹C。

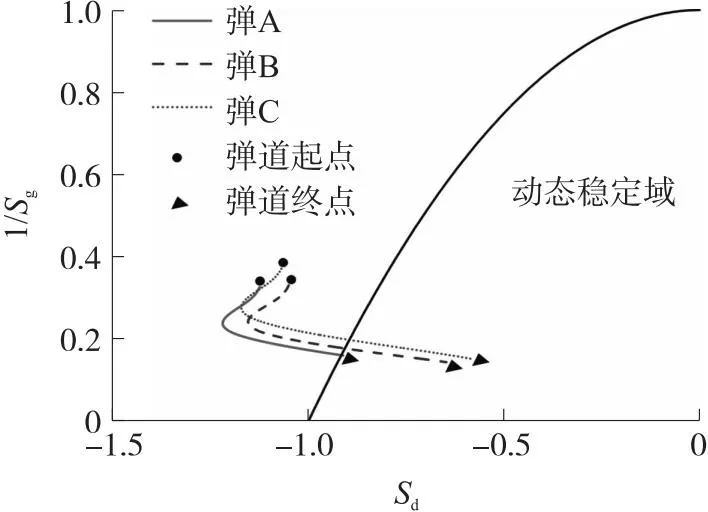
图5 不同结构参数弹丸飞行稳定性Fig.5 Flight stability of projectile with different structural parameters

表3 初始方案及仿真条件Table 3 Initial scheme and simulation conditions

弹A、弹B、弹C对应的风偏敏感因子分别为0.298 8,0.356 1,0.398 1。尽管弹A稳定性不佳,但风偏敏感因子要小于弹B与弹C,其主要原因为弹A的质量要大于弹B和弹C,在横风相同的情况下,侧偏方向上的速度和加速度小于弹B和弹C,因此其抗横风能力较强。

良好的结构参数设计可使弹丸获得更好的稳定性,即飞行时抗各种扰动的能力强,扰动引起的攻角、偏角小,收敛性好。特别是在受到横风强扰动作用时,抗风偏能力强意味着飞行弹道的侧偏变化小,对命中精度的影响也较小。

根据飞行稳定理论,当弹头的重心进行适当的前移时,弹头的外弹道飞行稳定度会提高,因此在弹头上进行合理的结构调整,可寻求弹头重心最前位置,即外弹道飞行稳定性最好的极限[17]。同理,将结构与气动外形联合设计,可寻求既满足稳定性又具有良好气动外形的弹丸。

2 优化设计建模与求解

2.1 优化设计变量的选取

①气动外形优化设计变量。

(7)

式中:RT为与给定前体长度相同的正切卵形半径,R为实际的头部圆弧半径。

②结构参数优化设计变量。

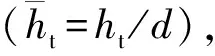
(8)

综上所述,将枪弹气动外形参数与结构参数进行联合处理,以上8个参数就是本文枪弹的优化设计变量,即:

2.2 优化目标函数

对于本文研究的这类弹头结构,除考虑外弹道飞行性能外,其作战任务中一般都有反轻装甲目标的要求。因此,将弹丸穿甲能力与抗风偏能力综合考虑,建立多目标优化模型,设计如下目标函数:

(9)

式中:ω1、ω2为加权系数,b0、α0分别为初始方案的穿甲厚度和风偏敏感因子,b和α分别为优化过程中的穿甲厚度和风偏敏感因子。其中弹丸穿甲厚度选用实际工程中常用的经验公式德马尔公式[18]计算:

(10)

式中:vc为穿甲前初速度即外弹道末速度;k是考虑钢甲机械性能等影响的修正系数,对于高硬度均质钢板,k约等于2 500;b即为所求穿甲厚度;m为弹头穿甲质量,枪弹的穿甲弹头除钢心外还有弹头壳和铅心,它们不能全部参与穿甲。因此,枪弹穿甲时的质量应该是:

m=mg+Δ(mq+mt)

(11)

式中:Δ为铜壳和铅心参与穿甲的百分数,可近似取为0.5[1]。

由德马尔公式可知,当弹丸结构参数和外弹道终点速度已知时即可计算其穿甲厚度b,同时,钢心所占比例越高穿甲质量越大,则b值越大,在一定程度上反映了铅钢混心弹丸的穿甲能力优于全铅心弹丸。

由式(9)的定义可知,优化目标是使b尽可能的大,α尽可能的小。为了将两个目标统一为单目标,设定两个加权系数满足ω1+ω2=1,ω1>0,ω2>0。在工程中应根据实际情况,经调试确定二者大小,如更加重视穿甲能力,则取较大的ω1值,本文算例中取ω1=0.5,ω2=0.5。

2.3 约束条件的确定

①外形参数约束。

②结构参数约束。

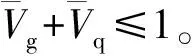
由于弹头的总质量为定值,因此在外弹道设计中初速和枪口转速保持恒定。为满足质量约束和弹头强度约束,由弹丸外形参数共同确定的弹心体积不能过大或过小,如弹心体积过大,即使全部填充密度较小的钢,在达到弹头规定的总质量情况下也无法填充至弹心体积的80%,同理,弹心体积过小则会存在即使将弹心充满密度较大的铅也无法达到弹头规定总质量的问题。

③稳定性约束。

弹身过长或重心位置过于靠后会影响弹丸稳定性,因此要求弹丸全弹道飞行过程中都满足稳定性条件,即陀螺稳定因子和动态稳定因子都应位于图1所示的动态稳定域内。

2.4 全局寻优方法

本文采用全局寻优能力较强的标准粒子群算法进行寻优[18],标准粒子群算法采用带有惯性权重的方式更新粒子速度,在一个D维的搜索空间中,有N个粒子组成一个群落,其进化过程为

vnj(t+1)=μvnj(t)+c1r1(t)[pnj(t)-xnj(t)]+
c2r2(t)[pgn(t)-xnj(t)]

(12)

xnj(t+1)=xnj(t)+vnj(t+1)

(13)

式中:n=1,2,…N;j=1,2,…D;c1和c2为学习因子;r1和r2为[0,1]范围内的均匀随机数;vnj为粒子速度;xnj为粒子位置;pnj和pgn为粒子个体极值和全局极值;μ为惯性权重,μ较大则全局收敛能力较强,反之则全局收敛能力较弱,局部收敛能力较强。

将寻优算法、弹丸外形与结构参数变量、气动力计算、弹道计算相结合,构建优化设计方案,在初速和枪口转速不变的情况下开展优化设计,具体流程如图6所示。

图6 优化设计流程图Fig.6 Optimized design flow chart

图6中气动力工程计算部分输出结果为弹丸的零升阻力系数、升力系数、静力矩系数、赤道阻尼力矩系数、极阻尼力矩系数以及马格努斯力矩系数,用于外弹道计算的模型采用六自由度刚体弹道模型,具体可参见文献[14]。

3 仿真优化分析

3.1 仿真条件

为验证本文所提的优化设计方法,以某12.7 mm全铅心枪弹为对象开展仿真分析,初始方案及仿真条件如表3所示。

3.2 优化结果与分析

对第2.2节建立的以风偏敏感因子最小和穿甲厚度最大为优化目标的函数进行寻优计算。为更好搜索到全局最优解,经反复试算,设置粒子群算法粒子个数为50,加速常数取为c1=c2=2,惯性权重取为μ=0.8,粒子群算法对目标函数的优化收敛历程如图7所示,经过41次迭代后开始逐渐收敛,各优化变量具体优化结果如表4所示。

图7 粒子群算法收敛曲线Fig.7 Particle swarm algorithm convergence curve

表4 优化结果与初始方案的对比Table 4 Comparison of optimization results with the initial scheme

由初始方案与优化方案结果可知,优化方案整体弹丸长度(52.18 mm)略大于初始方案。具体来看,优化方案弧形部变长,圆柱部和尾锥部则有所缩短。弹丸结构上,由全铅心弹丸变成了铅钢复合心弹丸,铜壳厚度也相应有所调整,铅钢总体占弹心的比例由71%上升至99%,弹丸结构优化结果如图8所示。

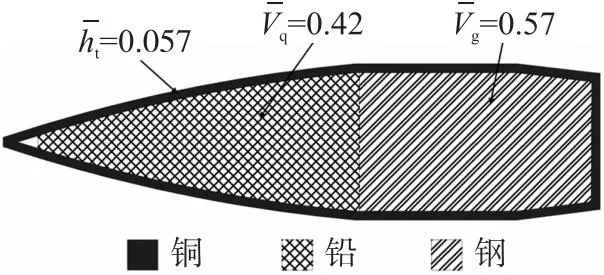
图8 弹丸结构优化结果Fig.8 Optimization results of projectile structure

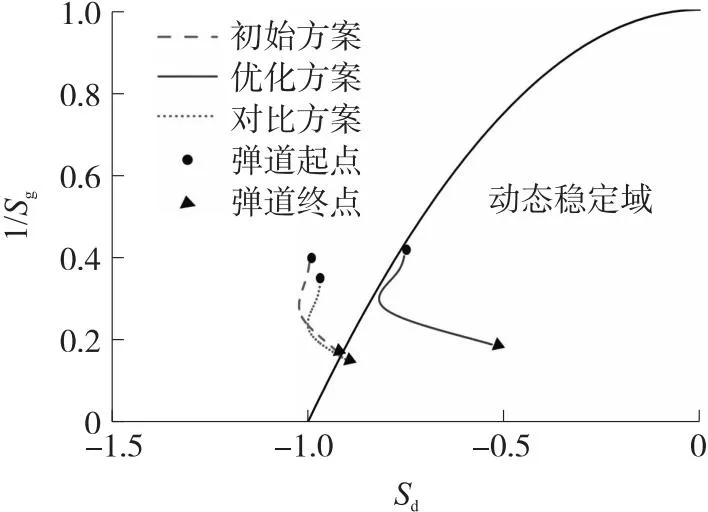
图9 不同方案飞行稳定性Fig.9 Flight stability of different schemes

由图9可见:优化方案的全弹道飞行过程都在动态稳定域内,稳定性较初始方案有较大提高。与对比方案相比,虽然具有相同的气动外形,但结构上质量分布的变化使得弹丸获得了更好的稳定性。

初始方案对应的α=0.397 9,b=5.52 mm,优化方案对应的α=0.332 5,b=7.83 mm。优化方案较初始方案风偏敏感因子减小了约16.4%,穿甲厚度提高了约41.8%。3种方案速度变化曲线见图10,初始方案飞行时间为1.49 s,落点动能为5 042 J,优化方案飞行时间为1.42 s,落点动能5 990 J。优化方案较初始方案飞行时间减小0.07 s,落点动能增加18.2%,优化方案在提高稳定性的同时,抗风偏能力、穿甲能力和落点动能均大幅度好于初始方案。

图10 不同方案时间-速度图像Fig.10 Time-velocity images of different schemes

同时,观察对比方案和优化方案,两者在速度变化方面几乎一致,说明气动外形是影响弹丸飞行速度的主要原因;通过弹丸材质的调整,优化方案的穿甲厚度较对比方案高出约24.9%,结构参数的优化使弹丸在气动外形相同的情况下获得了更好的稳定性和穿甲能力。综合来看,本文将气动外形与结构参数进行联合设计的方式解决了稳定性与气动外形设计之间的平衡问题,使弹丸在保证稳定性的前提下,获得了以抗风偏能力和穿甲能力最强为优化目标的气动外形与弹心结构优化结果,同时经验算,其存速能力同样优于初始方案。