基于热解动力学的喷管耦合传热数值研究

郑 健,杨玉龙,薛海峰

(1.南京理工大学 机械工程学院,江苏 南京 210094;2.南京晨光集团有限责任公司,江苏 南京 210006)

作为火箭发动机的能量转换装置,喷管在固体火箭发动机工作时要承受高温高压燃气的冲刷,由此带来的热防护问题给火箭发动机的安全带来隐患。碳/酚醛具有良好的隔热和耐烧蚀性能,当温度达到热解温度时,酚醛树脂会发生热解反应吸收热量,并释放出气体引射到边界层中,以达到热防护的目的;并且酚醛树脂热解之后会在表面形成炭化层,它具有良好的抗烧蚀性能[1]。因此,碳/酚醛作为耐烧蚀材料被广泛应用于火箭发动机喷管。

研究碳/酚醛材料在高温下热解炭化及传热特性时,通常采用炭化层,热解层以及原始材料层的多层结构模型[2-4],通过分别求解各层材料的热传导方程获得温度分布。研究表明,碳/酚醛材料的热解反应具有温度和时间相关性,在对其热物性变化过程进行描述时需结合热传导方程,求解不同时刻热解反应速率,获得碳/酚醛材料在时间和空间上的热物性变化规律。而碳/酚醛材料的热物性变化进而会对喷管的传热产生影响,为了得到喷管在工作过程中准确可信的传热数据,需要对这一物性变化过程进行描述。

一般情况下,喷管的尺寸参数依照最佳膨胀状态确定,但是在实际应用时由于外界压强的变化以及单室多推的实际需求,燃气也会存在过膨胀和欠膨胀状态。碳/酚醛材料在这3种工作状态下热物性参数变化也会有不同的趋势。研究者已经证明了耦合传热方法在喷管流固耦合问题的热量传输和结构温度场的计算中具有很高的可靠性[5,6],本文基于Fortran平台开发了一套变热物性耦合传热程序,对某型复合结构喷管在不同膨胀状态下的传热进行了数值仿真研究。在对程序进行验证之后,通过改变喷管入口的质量流率使喷管处于不同的膨胀状态,获得流体域和固体域的参数分布;并对喷管中使用的碳/酚醛材料因热解而产生的密度、比热容和热导率变化进行描述,得到了喷管在不同工作条件下热解炭化随时间和空间的分布。

1 数学与物理模型

1.1 流体域控制方程

根据Navier-Stokes方程的二维轴对称非定常可压缩流动形式结合k-ωSST湍流模型求解流体域,其方程形式如下[7]:

(1)

式中:U为守恒变量,Fc和Gc为对流通量,Fv和Gv为黏性通量,H为几何源项,nx,ny为边界单元法向向量。对流项采用三阶MUSCL格式进行离散[8],采用AUSM-PW+方法对控制体边界面的原始变量进行重构[9],对粘性项采用中心差分格式,采用Jacobian方法计算粘性通量偏导数。

由于碳/酚醛材料热解产生的热解气体对流场具有加质作用,需要在流场的控制方程中添加源项,Sf为根据碳/酚醛热解数学模型定义的源项。

1.2 固体域控制方程

1.2.1 基本假设

①对发动机工作初期进行仿真计算,忽略喉衬两端形成的喷管缝隙的变形。

②不考虑接触热阻和燃气辐射热。

③碳/酚醛材料受热生成的热解气体当前时间步存在于孔隙之中,下一个时间步即逸出引射到流体域中。

④碳纤维不发生化学反应,也不存在升华现象。

1.2.2 固体域热传导控制方程

采用导热微分方程求解固体域的传热特性:

(2)

式中:ρ为材料密度;t为时间;T为温度;cp为材料比热容;λx为材料轴向热导率,λy为材料径向热导率;SS为源项。对于本文研究的变热物性问题,假设在计算时间步内材料的热物性不变,采用有限体积法对式(2)进行求解,获取固体域的热传导特性。

1.2.3 源项表示方法

本复合结构喷管中,其收敛段和扩张段的隔热层均采用碳纤维/酚醛材料,所采用的源项SS由轴对称几何源项Ssh、酚醛数值热解潜热Ssl和热解气体逸出携带的能量Sse三项组成,计算公式如下[10]:

SS=Ssh+Ssl+Sse

(3)

其中:

(4)

式中:A0为热解反应指前因子;ρc为酚醛树脂完全炭化以后的密度;E0为反应活化能;hA为反应潜热;因为动能占总焓比例仅为1/108[11],故忽略热解气体的动能,hg为热解气体静焓。

由于碳/碳喉衬和钢壳体在发动机工作过程中不发生热解反应,故其源项只考虑轴对称几何源项。

热解气体对流场的加质作用可以通过添加源项实现,本数值模型考虑在靠近碳/酚醛材料的第一层流体网格内添加源项Sf,其实现方法如下。

①质量源项。

(5)

式中:δt为求解的时间步,ρt和ρt+δt分别为两个时刻的燃气密度;Vsj为固体单元体积。

垂直于边界方向的单元体,在单位时间步内产生的热解气体速率,定义为质量源项Sm,其表达式为:

(6)

式中:Vf为与燃气流场接触的一层网格体积。

②动量源项。

边界单元产生的热解气体将垂直于壁面喷射到流场中,在本计算模型中,Smv,x为沿x方向的动量源项,Smv,y为沿y方向的动量源项,其表达式如下:

(7)

(8)

式中:垂直x、y方向的面积分量分别用Aw,x、Aw,y表示,ρg为流场中的燃气密度。

③能量源项。

能量源项Sfe则表示从固体域逸出的热解气体注入到流场所携带的能量,其表达式为:

Sfe=-∑jSseVs,j/Vf

(9)

④组分源项。

在不同的温度,碳/酚醛热解会产生不同比例的气体组分。那么由于传热导致每个网格在不同时刻的温度不同,因此要计算每个时刻的不同气体组分,并进行求和计算:

(10)

式中:Vj为每个单元的体积;Yi为j单元i组分占总热解气体的质量分数;i为碳酚醛热解气体组分,i=1,2,…,4。

1.2.4 碳/酚醛热物性模型

①密度模型。

热解过程中,酚醛树脂的密度变化可以通过阿累尼乌斯方程求解的热解速率来表征:

(11)

式中:T0为碳/酚醛初始热解温度;当ρ<ρc时,碳/酚醛热解结束,其完全炭化。

在碳/酚醛材料中,酚醛树脂比例以及酚醛树脂的成碳率εc决定了ρc的大小,其表达式为:

ρc=εcΓρp+(1-Γ)ρcf

(12)

式中:在碳/酚醛原始材料中,Г为酚醛树脂所占的体积比,ρp为酚醛树脂密度,ρcf为碳纤维密度。

假设不同时刻的温度为常数,对式(11)进行积分得:

(13)

原始材料密度ρo可由下式表示:

ρo=Γρp+(1-Γ)ρcf

(14)

②比热容模型。

碳/酚醛热解简化模型假设:酚醛树脂在热解过程中一部分树脂瞬间热解成无定形碳和小部分气体,剩余部分维持原材料结构不变。因此碳/酚醛的密度则表示为:

ρ=σcpεcΓρp+(1-Γ)ρcf+(1-σcp)Γρp

(15)

式中:σcp为转化为无定形碳的酚醛树脂质量转化率;

农村土地流转是指农村家庭承包的土地通过合法的形式，保留承包权，将经营权转给其他农户或其他经济组织的行为。一般以土地承包经营权流转、集体建设用地使用权流转、宅基地使用权流转三种形式存在。

联合式(14)和式(15)求解,结果如下:

(16)

σp,σc,σcf分别表示酚醛树脂、热解形成的无定形碳和碳纤维3种材料组分的质量分数,其计算式为:

(17)

根据多组分模型得到的热解层比热容:

cp=σpcpp+σccpc+σcfcpcf

(18)

式中:cpp、cpc、cpcf分别为上述3种材料组分的比热容;当σp=0时,根据式(18)求得的cp为炭化层的比热容。

③热解气体的热物性模型。

酚醛树脂在高温热解后,其主要产物有甲烷、乙烯、乙炔、苯,其质量分数和摩尔分数分布见表1[12]。

表1 酚醛树脂热解产物Table1 Phenolic resin pyrolysis products

查阅JANAF表,热解气体各组分在不同温度下的定压比热容,可以进行分段多项式拟合,得到如下表达式:

cPi=a+bT+cT2+dT3+eT4

(19)

(20)

式中:T为气体温度;M为气体摩尔质量;σ为气体碰撞直径;Ωk为Lennard-Jones碰撞积分;R0为标准气体常数。求得各组分热导率λg,i之后,通过多组分气体混合物热导率公式可求得热解气体的定压比热容cp和热导率λg。

④热导率模型。

酚醛树脂热解产生热解气体逸出引射到流场,阻挡热流侵入,形成热阻塞效应[13],并在原始材料中形成大量孔隙,因此在进行碳/酚醛材料的导热计算时需要将空隙内部的热解气体纳入考虑范围之内。

本文所研究的碳/酚醛材料为各项异性材料,且其热解形成的孔隙与碳纤维方向有关[14],根据多孔介质理论的有效导热系数法[15],将多孔介质的传热问题折算为一般材料的相当导热问题,得到折算的垂直纤维方向和沿纤维方向的有效导热系数,分别用下标v和p表示:

(21)

式中:Гcf为碳/酚醛中的碳纤维体积分数,Гp为酚醛树脂体积分数,Гc为无定形炭体积分数;ψ为孔隙的体积分数,当酚醛树脂完全热解时,孔隙率ψc=(ρc-εcρp)/ρc,则:

(22)

ψ=ψcσcpГ

(23)

通过式(21)计算得到λv和λp,然后根据碳纤维在碳/酚醛材料中的实际排列方向,求解x,y两个方向上的热导率λx和λy。

1.2.5 碳/酚醛热化学烧蚀模型

发动机工作过程中,推进剂燃烧产生高温燃气中含有CO2和H2O气体,两者会发生异相反应,导致碳纤维/酚醛热防护层发生热化学烧蚀反应,其反应式如下:

(24)

①质量源项。

在式(24)中,热防护层壁面烧蚀反应消耗的碳质量流率由两部分组成,一是C与CO2反应消耗的碳质量流率;二是C与H2O反应消耗的碳质量流率。其表达式如下:

(25)

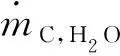
(26)

式中:pC,H2O和pC,CO2分别为H2O和CO2的分压,Aw为壁面的面积,kC,H2O、EC,H2O和kC,CO2、EC,CO2为化学反应动力学参数,其值见表2。

表2 化学反应动力学参数Table2 Chemical reaction kinetic parameters

将根据式(25)和式(26)计算得到的质量源项添加到靠近壁面的第一层流体网格上。

②动量源项。

烧蚀反应的产物以垂直于壁面的方式加质到流场中,Smv,x和Smv,y分布是x、y方向的动量源项,其表达式为:

(27)

式中:ρf为流体靠近壁面第一层网格的气体密度,Aw,x和Aw,y分别为该网格面在x、y方向定义的面矢量。

③能量源项。

发生烧蚀反应时会从流场中吸收热量,靠近壁面第一层网格的能量源项定义为:

(28)

式中:cp和TS分别为固体域耦合壁面处第一层网格的比热容以及温度。

④组分源项。

发生烧蚀反应也会造成壁面附近燃气组分的变化,为了能够描述异相化学反应造成的燃气组分随时间的变化过程,需要对各个组分分别添加质量源项。

(29)

式中:MCO2、MH2O、MH2、MCO和MC分别为CO2、H2O、H2、CO和C的分子量。

1.3 耦合传热方法

对流固耦合交界面采用保证温度连续、热流密度大小相等的处理方法实现耦合传热计算:

(30)

式中:流体在壁面处流动状态为层流,热导率λf=μcp/Pr;将两式联立即可得到界面处温度:

Tw=(ΔyfλyTs+ΔysλfTf)/(Δyfλy+Δysλf)

(31)

将壁面温度Tw分别代入流体域与固体域,重新求解其边界条件就可以实现对流体域和固体域的耦合传热。

2 算例验证

采用11英寸陶瓷风洞中获得的钝头碳/酚醛试件气动加热实验结果,验证本文所开发程序的准确性[16],来流的总压为4.97×105Pa,总焓为2.55 MJ/kg,碳/酚醛试件的几何参数如图1所示。本文使用转化为无定形碳的酚醛树脂占原始材料中酚醛树脂的质量分数σcp表示炭化程度,将其定义为炭化率,σcp为1时表示酚醛树脂完全炭化,此时材料只包含碳纤维和无定形碳。此处使用炭化率值为0.99位置作为炭化层与原始材料边界。将文献中给出的试样头部表面的温度测量结果、炭化层边界与程序计算结果进行比较,结果如图2所示。可以看出,表面温度和炭化层边界的仿真结果与实验数据相符,验证了本文使用的变热物性耦合传热程序的准确性。

图1 钝头碳/酚醛试件几何参数Fig.1 Geometric parameters of blunt carbon/phenolic specimens

图2 流体域计算网格Fig.2 Fluid domain calculation grid

该验证算例采用轴对称模型对流固区域的传热特性开展数值仿真,计算网格如图2和图3所示。

图3 固体域计算网格Fig.3 Solid domain calculation grid

钝头碳/酚醛试件头部表面的温度测试结果、炭化层边界与程序计算结果的对比见图4。由图可见,其表面温度及炭化层边界的仿真结果与实验结果相符,验证了本文所编制的程序在求解耦合传热中的准确性。

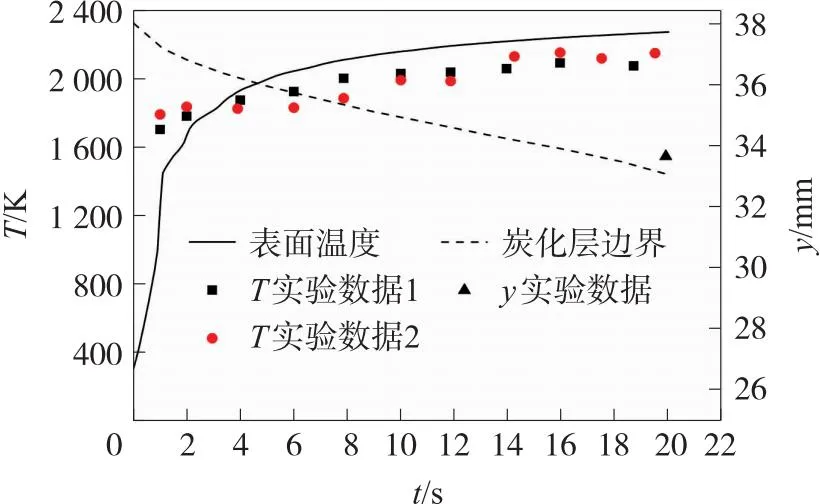
图4 驻点处表面温度、炭化层边界仿真结果和实验结果Fig.4 Simulation and experimental results of surface temperature at stagnation point and boundary of carbonization layer

3 计算结果及讨论

本文研究的复合结构喷管扩张比为2.7∶1,喷管喉径为82 mm,喷管外壳和喉衬分别为45钢和C/C复合材料,本文研究重点为碳/酚醛材料的热物性参数变化,因此仿真计算中将C/C复合材料视为各向同性材料;碳/酚醛采用模压制造工艺,其组分的物性参数如表3所示。

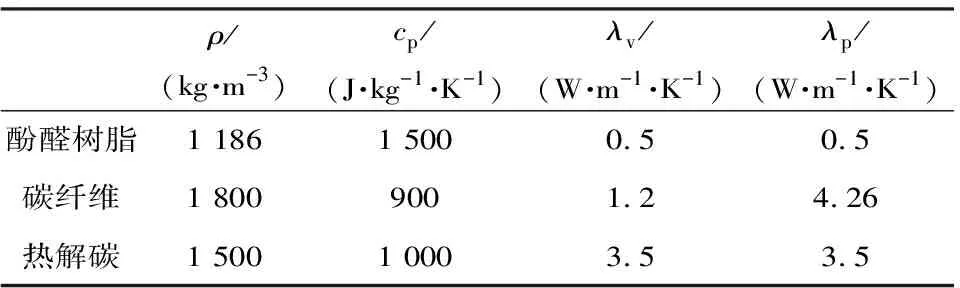
表3 碳/酚醛各组分物性参数Table 3 Physical properties parameters of carbon/phenolic components

通过改变喷管入口的质量流率,对喷管处于过膨胀、最佳膨胀和欠膨胀这3个状态分别进行传热研究,入口质量流率分别为4.5 kg/s、17.3 kg/s、20 kg/s。仿真计算模型和网格如图5所示。喷管入口燃气的总温T0为3 200 K,比热比γ为1.26,气体常数R为320 J/(kg·K);数值仿真中在壁面处加入了5个监测点,以监测各点处的温度随时间的变化,其具体位置如图6所示。

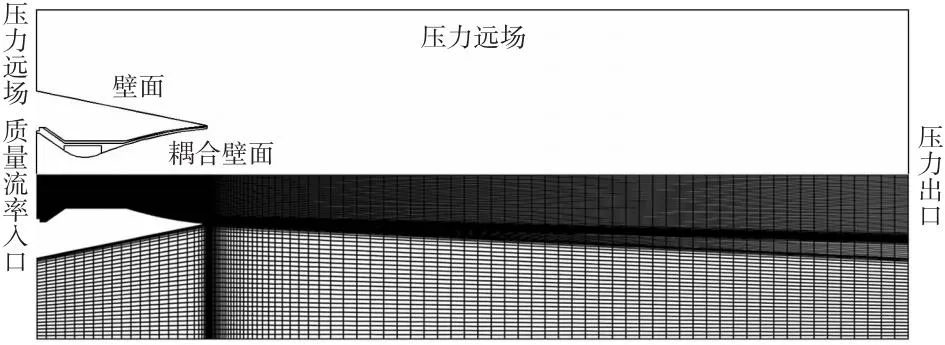
图5 网格划分及边界条件Fig.5 Mesh generation and boundary conditions

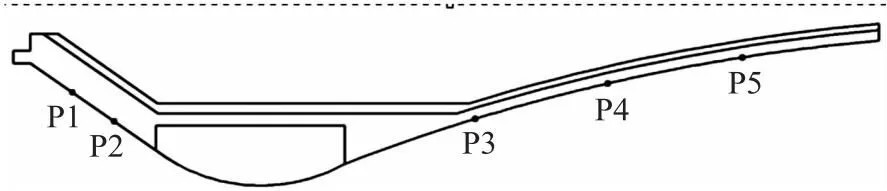
图6 壁面监测点Fig.6 Wall monitoring Points

3.1 流场仿真结果分析

不同入口质量流率条件下的马赫数云图如图7所示,从图中可以看到,质量流率为4.5 kg/s时,喷管出现了分离流动并形成一道斜激波;质量流率为17.3 kg/s时,喷管处于最佳膨胀状态,流场流动状态与质量流率为20 kg/s时相似。图8为不同质量流量条件下壁面附近的压力分布,三个质量流率条件下壁面附近压力沿轴向总体呈递减趋势,但在收敛段入口位置均出现了一道压力峰,经过收敛段和喉衬之后持续减小并在喉衬与扩张段的材料交界面均出现了压力增加,入口质量流率为4.5 kg/s时在0.36 m位置出现了分离流动,在分离点之后压力逐渐升高直到达到环境压力。

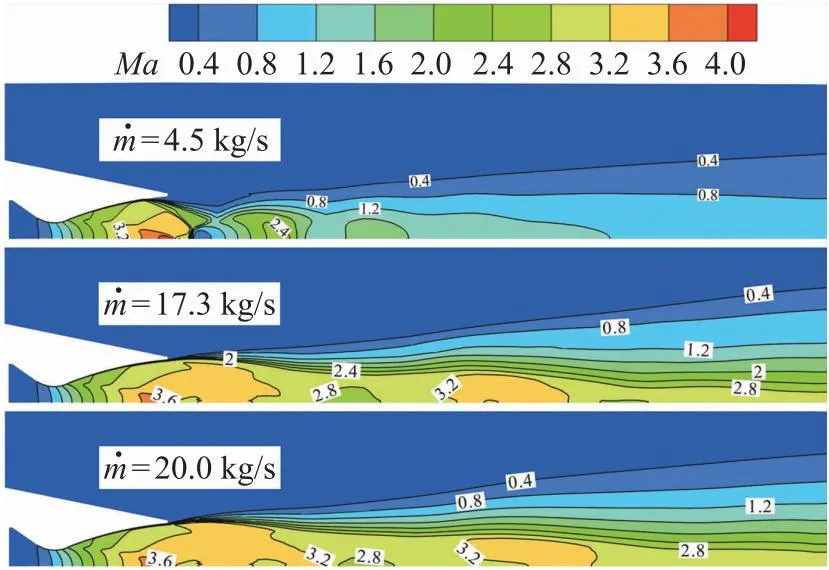
图7 不同质量流率下马赫数云图Fig.7 Mach number cloud map under different mass flow rates

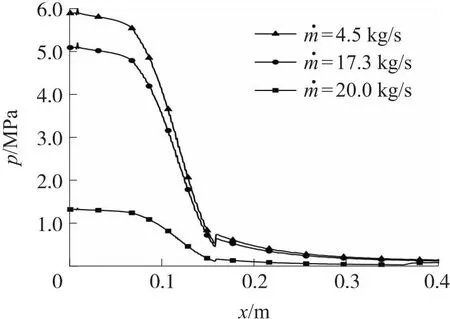
图8 喷管内壁面压力分布Fig.8 Pressure distribution on the inner wall of the nozzle

3.2 耦合场仿真结果分析

发动机开始工作后,喷管受到高温燃气加热作用开始升温,而在喷管不同位置流动参数不同,壁面温度和热流密度分布也有差异。图9为1 s时不同质量流率条件下喷管内壁面的温度分布,从图中可以看到对于没有流动分离的情况,温度在喷管等直段下降,在收敛段温度沿轴向上升,在扩张段温度沿轴向下降,与单一材料喷管计算结果不同的是,在喉衬位置温度没有达到最大值,并且呈沿轴向降低趋势,温度在喉衬与碳/酚醛材料的交界面附近出现极大值和极小值,这是由材料的不同热物性参数导致的。质量流率为4.5 kg/s时,由于在喷管扩张段出现流动分离,在0.36 m位置壁面温度突然升高,之后又快速下降。

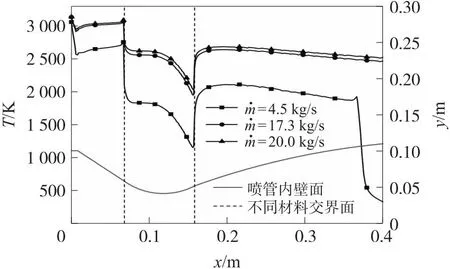
图9 t=1 s壁面温度分布Fig.9 Wall temperature distribution at t=1 s

图10为耦合壁面热流密度的分布,此处规定热量从流体域传递到固体域符号为正。可以看到,在喷管入口平直段热流密度逐渐减小并在拐角位置热流密度增加,在收敛段和扩张段热流密度维持在较低水平并且变化不大,与温度分布曲线相同,突变也发生在材料的交界位置,在喉衬位置热流密度量级大于碳/酚醛材料表面热流密度,并在喉部热流密度达到最大值。喷管出现分离流动时,由于分离点之后气体温度较高,分离点处热流密度会突然升高,之后急剧下降;分离点之后热量由碳/酚醛材料传递到气体,热流密度为负值,而在分离点下游距离分离点越远,壁面温度越低,热流密度沿轴向逐渐升高直到变为0。

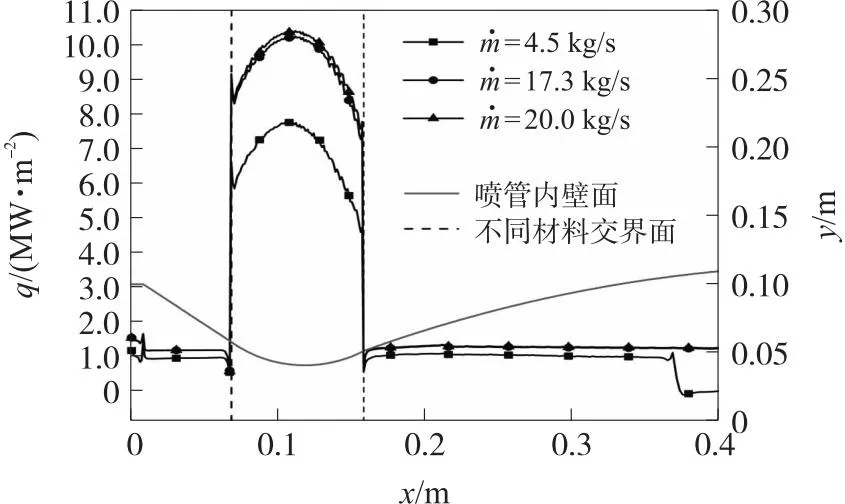
图10 t=1 s耦合壁面热流密度分布Fig.10 Coupled wall heat flux density distribution at t=1 s

图11为喷管内壁面5个监测点的温度在各个工况下随时间变化曲线,可以看出在每个工况下各点温度随时间增加趋势相近,并在t=1s时温度变化开始趋于稳定,对于本文研究的3个工况,喷管入口质量流率增大引起壁面附近压力增加,进而引起对流换热强度增加,同一时刻同一位置壁面温度增加。

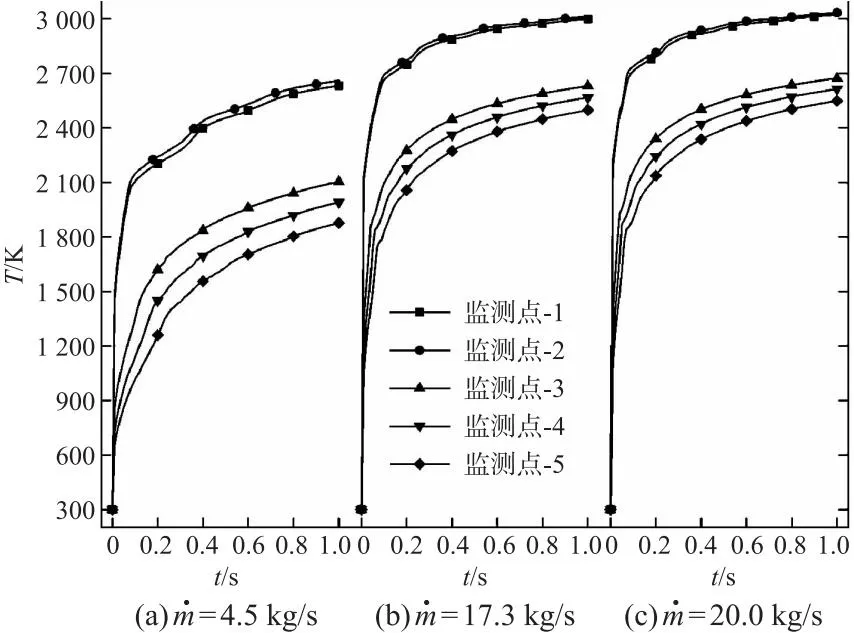
图11 监测点温度随时间变化曲线Fig.11 Temperature variation curve of monitoring points over time

图12和图13分别为0.5 s和1 s时刻3个工况下的炭化层厚度沿轴向变化曲线,在收敛段部分,炭化层厚度在入口位置最小,沿轴向逐渐增加,由于在与喉衬交界位置热流密度较大,炭化层厚度在该区域最大,如图14与图15所示。

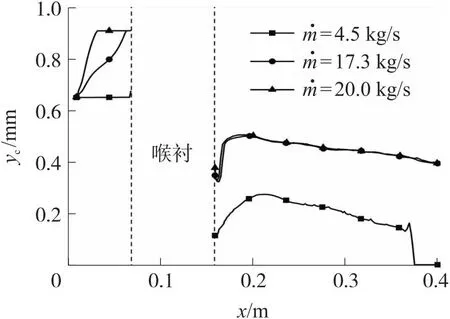
图12 t=0.5 s炭化层厚度沿轴向变化曲线Fig.12 Curve of axial variation of carbonization layer thickness at t=0.5 s

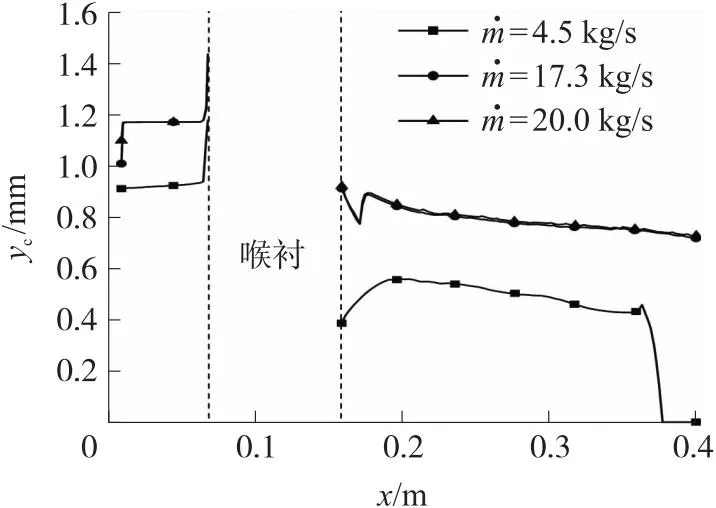
图13 t=1 s炭化层厚度沿轴向变化曲线Fig.13 Curve of axial variation of carbonization layer thickness at t=1 s

图14 t=0.5 s喉衬附近孔隙率云图Fig.14 Cloud map of porosity near the throat liner at t=0.5 s

图15 t=1 s喉衬附近孔隙率云图Fig.15 Cloud map of porosity near the throat liner at t=1 s

对于没有出现流动分离状态,扩张段部分炭化层厚度变化趋势与时间相关,发动机工作之后炭化层厚度最大值位置在0.19 m,与扩张段温度最大值点相近,而随着时间推进在与喉衬交界位置炭化层厚度继续增加直至在该处形成扩张段内最大区域,从图中也能直观看出在喉衬两端炭化层厚度增加,并且随时间推进变化增大。当扩张段内出现流动分离,炭化层厚度最大值区域出现在交界面之后,并且随时间推进最大值区域向喉衬方向移动;在分离点处由于壁面温度、热流密度较高,炭化层厚度突然增加,之后沿轴线迅速下降。

4 结论

①喷管内壁面热流密度在收敛段和扩张段变化较为平缓,由于喉衬的热导率较大,其表面热流密度与碳/酚醛材料表面热流密度出现量级差异,并在与收敛段交界面位置引起热流密度突增,在分离点气体与壁面对流换热作用增强。

②收敛段的炭化层厚度大于扩张段炭化层厚度。对于收敛段,炭化层厚度沿轴向增加,在与喉衬接触面附近增加明显,并且随时间推进增加幅度越剧烈。对于扩张段,没有流动分离情况下,发动机工作初期炭化层厚度与温度分布趋势相近,但由于喉衬部分的热流密度较大,随时间推进与喉衬交界面位置炭化层厚度逐渐增大,直至该区域形成炭化层厚度最大区域;当扩张段出现流动分离,分离点处炭化层厚度突然增加,之后炭化层厚度沿轴线逐渐减小,直至变为零。