基于改进DQN方法的滑翔制导炮弹弹道规划

谢蕃葳,王旭刚

(南京理工大学 能源与动力工程学院,江苏 南京 210094)

超远程滑翔制导炮弹滑翔段的弹道规划一直以来都是研究的重点和难点,其既要满足宽空域宽速域飞行过程中的强耦合、快时变以及强非线性的运动约束关系,还需要在被限制的控制空间内寻求最大作战射程[1,2]。滑翔段的弹道规划的实质是求解非线性带约束最优控制问题,对应的动力学模型是时变非线性微分方程组。随着非线性条件和约束条件的增多,目前该方程组难以通过解析的方式求得目标解。因此,现在的弹道规划方法主要归纳为三类:间接方法[3,4]、直接方法[5,6]和智能启发式方法[7-9]。

深度强化学习是采用深度神经网络做函数拟合的一类新兴强化学习算法,它不同于依靠大量最优弹道数据样本进行弹道规划训练的深度学习方法[10],而是通过与环境的自主交互寻求最优规划网络参数。目前,强化学习的相关应用已经在围棋[11]、电子竞技[12]等场合中展示了在复杂环境下处理各种信息,并将信息转换为规划决策的能力。目前,基于深度强化学习的飞行器弹道规划研究仍处于起步阶段。文献[13]在设定初速度与出射角的情况下,在弹丸的外弹道飞行过程利用Q-learning算法输出控制指令,通过强化学习迭代计算实现弹道优化目标,导弹射程比无控时明显增加。文献[14]提出了一种基于网络优选双深度Q网络的深度强化学习方法,保存了训练过程当中的最佳网络,突出了算法优越的性能表现。但文中对奖励函数的落速惩罚没有指明,没有明确的约束限制指向。文献[15]提出了一种无模型的强化学习和交叉熵方法相结合的在线航迹规划算法,利用近端策略优化算法离线训练智能体,可以在复杂多变的飞行空域中生成曲率平滑的航迹,拥有较高的突防成功率。文献[16]利用深度确定性策略梯度算法训练得到巡飞弹突防控制策略网络,在1 000次飞行仿真下拥有82.1%的任务成功率,平均决策时间仅有1.48 ms。

然而,以上深度强化学习算法研究的重点主要集中在算法的应用性能上,算法本身的稳定性研究方面稍有欠缺。强化学习的相关研究领域普遍存在着训练不稳定的问题。所以,为了建立稳定的深度强化学习训练过程,本文以超远程滑翔制导炮弹滑翔段作为研究对象进行弹道规划,创新性提出了一种IM-DQN算法,采用无效经验剔除的经验池管理方法,将训练过程中整体表现低效的回合样本点全部剔除以保证提取样本时避开这些低效环节,并且添加探索限制策略进行更新,保证训练网络效果不会大幅度跌塌,使得训练效果更加稳定。

1 问题描述

滑翔制导炮弹在弹道顶点展开鸭舵进行滑翔,本文聚焦智能规划方法在滑翔段的适用性问题,为了突出研究问题的重点,给出了典型滑翔运动模型,攻角为控制参数,其三自由度运动模型为[17]:

(1)

式中:x、y是惯性坐标系下的位置,v、θ、m分别是炮弹飞行速度、弹道倾角、炮弹质量。阻力Fx和升力Fy计算公式如下:

(2)

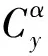
超远程滑翔制导炮弹的弹道规划往往期望在有限制条件下实现最大射程,因此将连续问题离散化,建立目标优化函数。

(3)

式中:vf表示落速,vc为落速限制,tf表示终止时间。xa表示离散后一个步长ts内通过执行a动作得到的航程距离。

针对滑翔段轨迹优化问题,提出用深度强化学习方法训练深度神经网络,将非线性规划问题离散化,转化为序列决策问题。它根据此时的状态和内置深度神经网络可以在毫秒级快速输出对应的控制动作,然后迭代状态和控制指令得到一条最优规划曲线,避免了在飞行过程中求解复杂的非线性规划问题,通过地面训练的方式减少了空间飞行过程中的计算量,规划流程如图1。

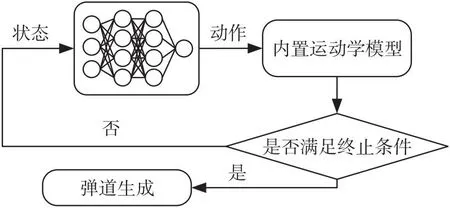
图1 基于神经网络的弹道规划Fig.1 Trajectory planning based on neural network

滑翔初始数据参数设定见表1。

表1 滑翔初始参数设定Table 1 Initial glide parameter setting

本文研究的是滑翔段无动力滑翔,为保证飞行过程中的稳定性,飞行过程中的控制量具有严格限制,设置攻角幅值的约束为α∈[0,12°],综合考虑寻优空间的大小与寻优时间的长短,将控制攻角离散化,控制攻角取值为0～12°之间的整数。

2 基于强化学习方法的弹道规划

2.1 DQN方法

DQN方法起源于Q-learning方法,采用一个价值表格记录下每个状态下的动作,并且赋予每个动作相应的值,以表明此状态下各动作的优劣。但随着状态空间和动作空间的变大,整个价值表格的容量空间也会随之变大,如果状态空间是连续的,则无法使用Q-learning方法。因此,Q-learning方法可以解决离散状态空间问题,而无法解决连续状态空间问题。面对此类连续空间问题,DQN采用一个神经网络结构代替价值表格,即动作价值网络Q(st,at,μi),输入当前的状态和动作即可得到相应的动作价值Q值,解决了连续空间状态维度爆炸的问题。

为了使训练过程更加稳定,DQN算法采用了相同神经元个数和参数配置的双网络结构,分别是当前评估价值网络μ和目标价值网络ω。在每次训练开始前,在给定的参数范围内初始化状态参数;在训练过程中,动作的选择遵循贪心策略,即在开始训练的一段时间内,网络模型会在动作空间内随机选择动作,但随着训练的不断推进,一段时间后会逐步根据当前的动作价值网络的最大值选择最优动作。

根据当前状态和动作输出下一阶段的状态参数,输入当前经验样本et=(statrtst+1)到记忆经验池容积De=(e1e2…et)当中,记忆经验池方法有效打破了样本之间的关联关系,提高了数据利用率,每一次在固定时间步长之后从经验池容积当中提取小批量样本重新计算其动作价值,DQN算法误差更新如下式[18]:

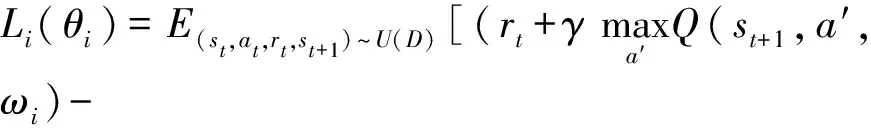
(4)

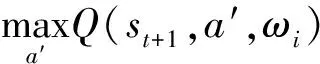
2.2 IM-DQN算法

传统DQN方法在前期训练的时候,参数通过经验池样本中随机抽取一批样本进行更新,里面包含的低性能数据样本,不利于网络模型的最优解。本文提出IM-DQN算法,在传统DQN的原先经验池方法[19]基础上添加优秀经验保存,在更替网络方面添加了限制探索率的策略模式,具体实现过程如下:

①优秀经验保存会剔除表现低效的整个回合样本点,只保留优秀回合样本,网络模型在随机抽取样本的时候不再从低效回合样本中学习经验。

②传统DQN方法在每固定回合后,无条件将目标价值网络参数替换为评估价值网络参数。限制探索率方法与之相比增加了一个限制探索率,如果多次训练出来的评估价值网络的一个回合奖励值低于目标价值网络的一个回合奖励值乘以限制探索率的值,则这次更新停止反而将评估价值网络重新替换为目标价值网络,否定了网络模型这一轮回合的探索工作。IM-DQN算法流程[20]如图2所示。

图2 IM-DQN算法流程框图Fig.2 Flowchart of Improved DQN algorithm

2.3 基于IM-DQN算法的弹道规划

本文将IM-DQN算法思想移入到弹道规划当中。算法采用了3步式的设计思路:状态空间设计、状态转移方式设计以及奖励值函数设计。

状态空间设计:针对滑翔段飞行场景,滑翔制导炮弹滑翔横向距离x、当前高度y、飞行速度v、弹道倾角θ及动作值作为状态空间,定义为S=(xyvθα)。

状态转移方式设计:在IM-DQN算法当中,确定当前状态参数之后,动作价值网络本身就是策略网络,在有限的动作空间内选取最大动作,相当于一个非线性函数映射当前状态下最佳动作。确定了当前状态、动作选取以及运动学模型,再通过数值方法求解相关非线性方程确定下一状态参数。

奖励值函数设计:为提高样本效率和完成约束限制条件,本文采取连续奖励项和惩罚项相结合的奖励函数设置,设计如下式所示:

r(s)=rx+rp

(5)

式中:rx为每一步的航程奖励函数,只与当前点到初始点的距离有关。rp为约束惩罚项。综合以上两点,现对奖励函数具体设计如下式:

(6)

(7)

设置rx的目的是压缩每一步的奖励,促使着滑翔制导炮弹朝着更远的方向飞行。设置rp的作用是在炮弹落速低于约束限制之后给予一个惩罚措施。需要注意的是,相比于最优控制求解过程的强制约束,DQN的约束往往呈现的是一种弱约束限制,它只是促使着弹道规划落速朝着限制点运动,结果不一定严格满足约束,而是在约束附近摇摆不定。

IM-DQN在训练过程中的步骤如下:

①初始化记忆经验池De,设置神经网络的超参数,初始化评估价值网络μ和目标价值网络ω。

②外循环:初始滑翔制导炮弹的滑翔起点状态参数s0,然后进入到内循环当中。

③内循环:内循环是一个训练回合里面的工作循环。首先在每一步由贪心策略选取动作a,执行动作a即可得到下一状态st+1,采用优秀经验保存机制存放(starst+1)到经验池De当中;在隔了N个步长后将经验池De中随机采样一批样本(si,a,r,si+1)进行价值判定,当提取的样本满足终止条件时:yj=rj,而在其它情况下,其价值均为:yj=rj+γmaxa′Q(st+1,a′,ω),再进行梯度计算loss=[yj-Q(st,at,μt)]2,以此更新评估网络μ。传统DQN算法是在一定步数后无条件更换目标价值网络,而IM-DQN算法会根据限制探索率进行更新,若满足更新限制率,则ω=μ,反之则μ=ω。

3 仿真实验设计及结果分析

3.1 实验仿真流程及参数设置

本文以滑翔制导炮弹为研究对象开展弹道规划,为了更大程度模拟真实作战情况以及探索更多状态空间,训练过程中在表1的滑翔参数基础上添加随机扰动:滑翔初始高度为57.5～58.5 km,初始速度为1 250～1 300 m/s,初始弹道倾角为-3°～0°。网络学习率设置为η=0.01,折扣因子γ=0.99,经验池容量ND=20 000,采样规模ba=64,训练时间步长设置为5 s。仿真实验全部网络采用同一种结构,设置两个隐藏层,每层64个神经元,中间全部采用tanh激活函数进行连接。具体网络结构及激活函数设置设计见表2。为更直观的显示规划算法性能表现,设置参照组最大升阻比方法、GPM方法与强化学习算法进行横向性能比较。

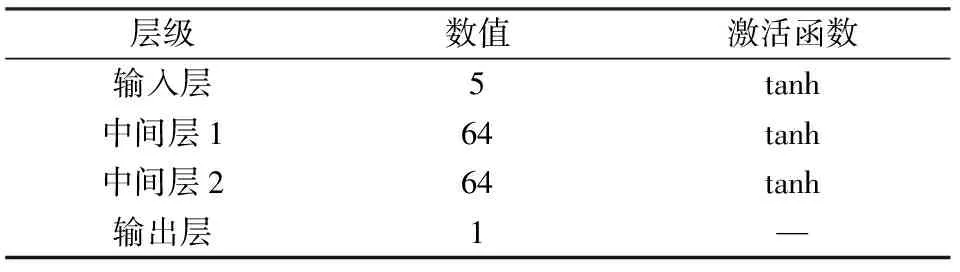
表2 网络结构Table 2 Network structure

考虑到最大升阻比方法无法对落速进行约束,本文设计了两种实验,最大升阻比方法、DQN方法、IM-DQN方法3种实验在无落速约束条件下进行仿真对比;GPM、IM-DQN方法2种实验在有约束条件下进行仿真对比。

3.2 无落速约束仿真

无落速仿真实验选择rx作为奖励函数,不再考虑惩罚约束项。为更方便观察奖励值的变化趋势,本文设计每100个值取一次平均值作为平均奖励值点。分别设计DQN和IM-DQN算法在10 000、30 000和50 000这三组不同训练回合下的对比实验,为尽可能减少训练过程的偶然性对实验的影响,每种回合分别训练10次取其中最优网络参数。两种方法的具体奖励趋势如图3和图4所示。

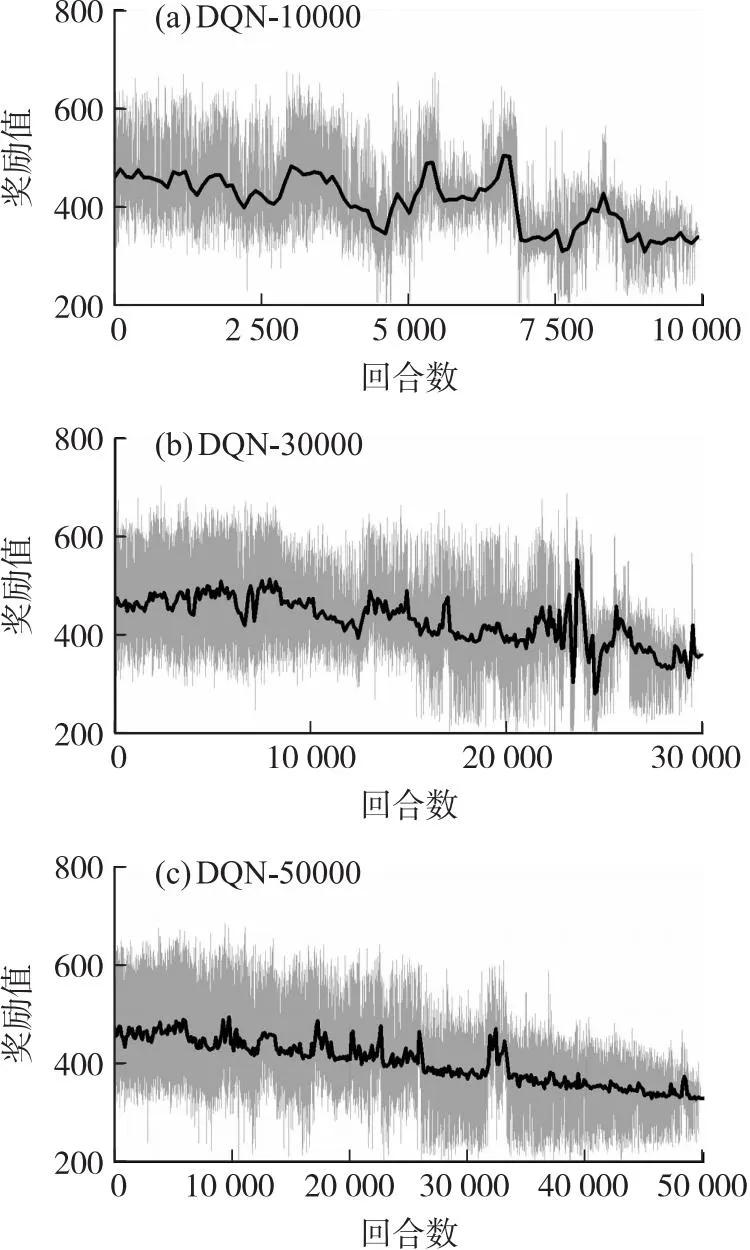
图3 无约束下的DQN算法奖励趋势图Fig.3 Unconstrained DQN algorithm reward trend graph

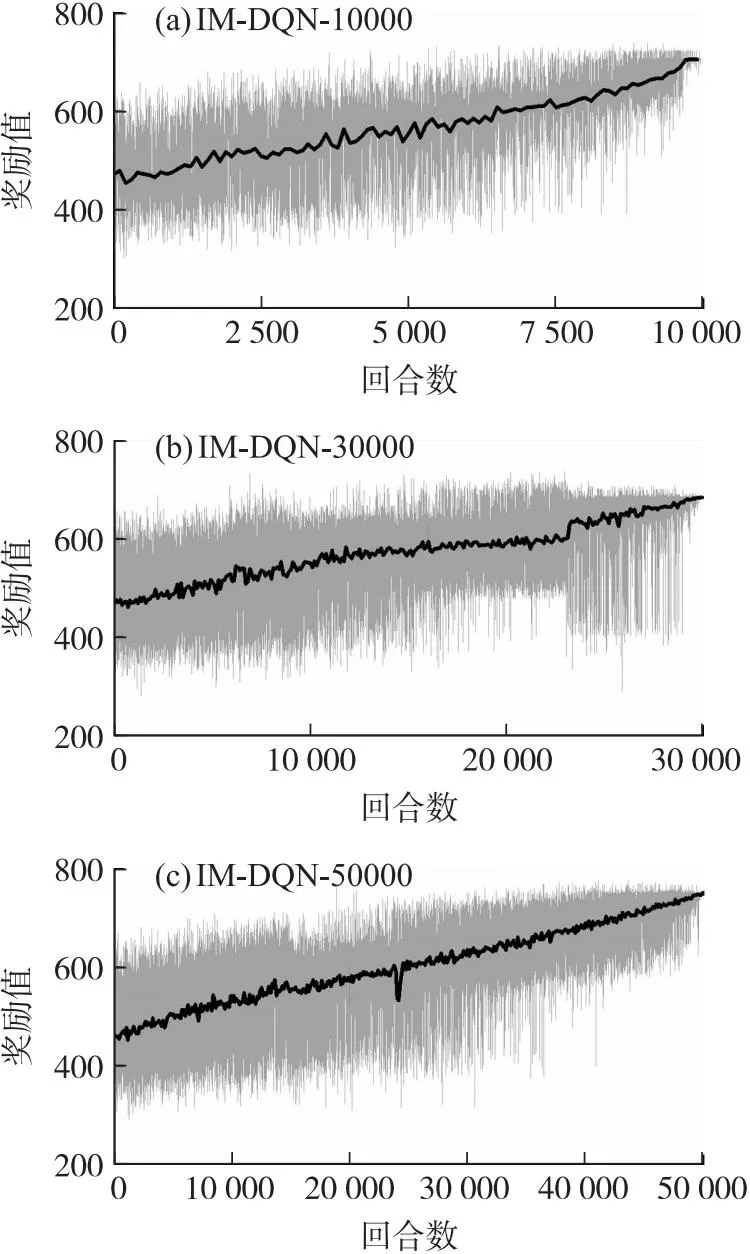
图4 无约束下的IM-DQN算法奖励趋势图Fig.4 Unconstrained IM-DQN algorithm reward trend graph

从上面奖励趋势图可以得出,传统DQN算法的训练过程呈现出一种强随机性,它的最终序列动作很难寻求到航程最优值。反观IM-DQN方法,在不同回合下它们的奖励值全部呈现一个逐步上升的趋势。表3为两种方法的最终训练结果。

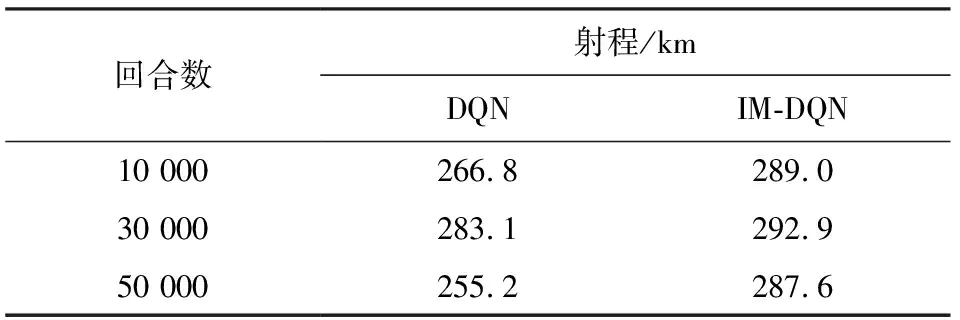
表3 无约束下两种算法的最优训练结果Table 3 The optimal training results of the two algorithms without constraints

根据对比结果看出IM-DQN方法训练结果更加稳定。两种算法皆在30 000训练回合数达到航程最大值,故选取30 000回合数作为最终训练回合数。本小节对比了IM-DQN方法、DQN方法和最大升阻比方法,3种算法的性能表现如图5所示。

图5 3种算法下的性能效果Fig.5 Performance effects of the three algorithms

对比图5的仿真结果可以得出,IM-DQN方法相较于DQN方法和最大升阻比方法的射程都有所提升,其中相较于DQN方法和最大升阻比方法分别提升了9.8 km和19.5 km,说明IM-DQN方法在无约束条件下具有较好的优化性能。飞行过程中该方法对应的速度曲线相较于其它两种方法更加平滑。3种方法的具体性能如表4所示。

表4 无约束下的三种方法性能比较Table 4 Performance comparison of three methods without constraints

3.3 有落速约束仿真

有落速约束下的奖励函数选用公式(5),完整考虑连续奖励项和约束惩罚项。在有落速约束下选取合适的训练回合次数,同样设置10 000、30 000和50 000共3组不同训练回合,每组重复训练10次,各选其中性能表现最好的一组作为实验参照组。为观察奖励值点的位置情况,3种训练回合下皆以等差的形式取400个点作为观察对象。奖励值点及其相关表现如图6和图7所示。

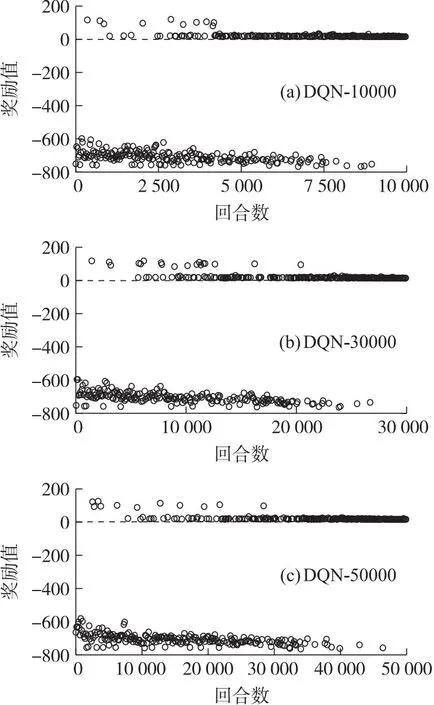
图6 有约束下的DQN算法奖励值点图Fig.6 Constrained DQN algorithm rewards value point plot

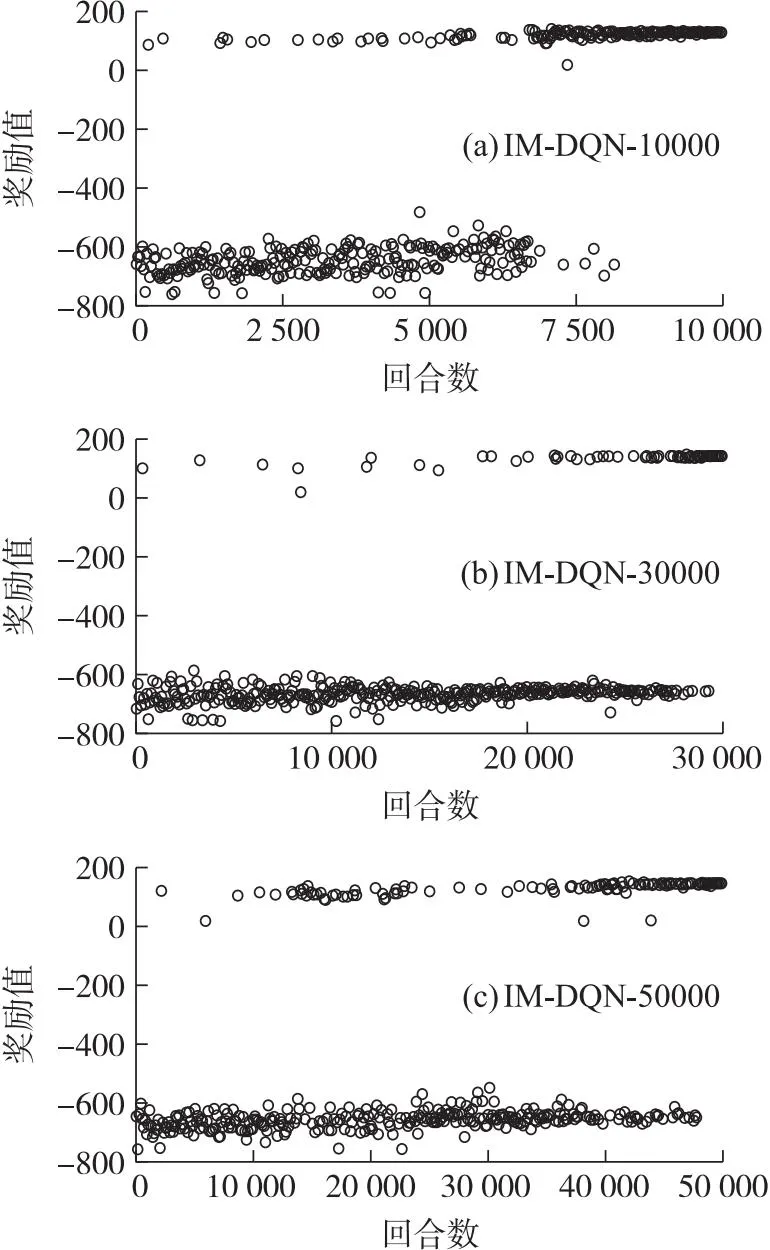
图7 有约束下的IM-DQN算法奖励值点图Fig.7 Constrained IM-DQN algorithm rewards value point plot

由图6和图7可以得出,两种方法的奖励值点在不同训练回合的末端皆落于零值以上,说明两种训练方法都可以良好的满足落速约束限制。但从性能表现来看,IM-DQN方法训练结果的奖励值点最后在150附近起伏,而DQN方法的3种训练回合的结果奖励值仅有15,在图6中基本与右零刻度线重合,说明了航程性能上的差异。两种方法的具体性能如表5所示。

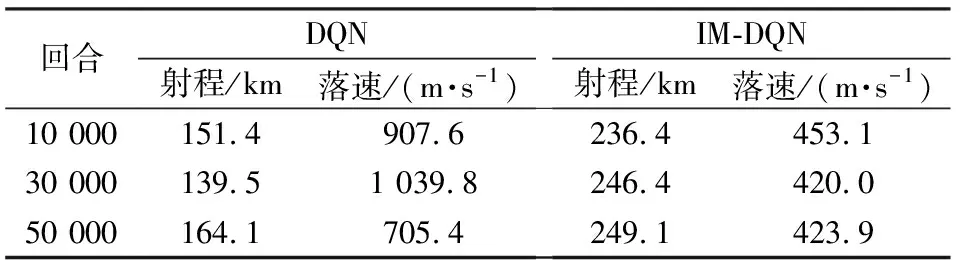
表5 有约束下两种算法的最优训练结果Table 5 Optimal training results of two algorithms under constraints

根据上述仿真实验结果可知,在有限次数训练下,传统DQN方法的性能效果完全无法跟相同训练回合下的IM-DQN方法相比。在有约束条件下,DQN方法难以寻求到最优动作价值网络,它仅仅满足了约束限制,但不能在有约束下寻求最优。从不同训练回合可以看出DQN方法随着训练回合数增加,网络性能逐渐发生变化,这种情况说明要想通过DQN方法完全体现出其最优性能网络可能还需要更多的训练回合数,这同时也延长了前期训练的准备时间,不利于实际作战的应用。从图7及表5可以得出,不同于于无约束情况下,当问题复杂之后,随着训练回合的增多,网络所呈现的效果也就越好,综合考虑下选取50 000训练回合数的神经网络作为有约束下的动作价值网络。为观察IM-DQN具体性能表现情况,本小节设计基于最优控制理论的高斯伪谱法作为仿真对比参照组,通过GPOPS工具箱可以得到最优控制规划曲线。IM-DQN方法与GPM的具体性能效果对比仿真如图8所示。

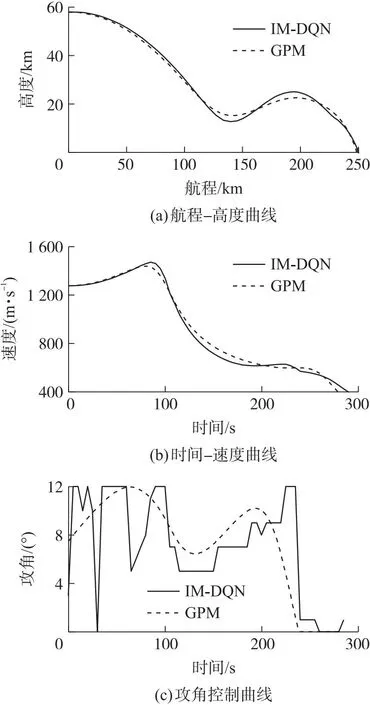
图8 两种算法下的性能对比效果Fig.8 Performance comparison between the two algorithms

图8和表6是IM-DQN和GPM算法的性能结果对比,由图可以得出IM-DQN方法规划曲线与GPM十分相似,甚至结果值还略高于GPM,这也展示了强化学习在与环境交互过程中的优越性能,它拥有着在约束条件下寻求最优性能网络参数的能力。强化学习之所以可以在有约束条件下寻求到了最优性航程网络参数,是因为深度强化学习在探索过程中带有记忆性,并且赋予这种记忆价值,这种价值不同于深度学习限制于数据样本自身的局限性,强化学习的记忆基于与环境的交互过程,在环境交互中评定动作的优劣程度,使得深度强化学习可以突破单纯深度学习的局部样本最优解。但在神经网络训练过程中有许多因素会导致网络性能崩塌,本文IM-DQN方法添加了低效经验池剔除和探索限制率的组合策略,使得网络的鲁棒性更高,不容易在训练过程中发生崩塌。随着学习过程的逐渐增加,网络也积累着更多的知识从而做出更优的指令。

表6 有约束下的两种方法性能比较Table 6 Performance comparison of two methods under constraints

4 结论

本文利用强化学习与环境交互的特点,提出了一种基于IM-DQN的滑翔制导炮弹弹道规划方法,在传统DQN算法的基础上,利用低效经验池剔除加限制探索率策略,有效解决了传统DQN学习效率低,奖励曲线方向不明确的问题。仿真结果证明,IM-DQN方法很好地解决了传统强化学习方法在寻求最优控制过程中网络崩塌现象无法寻求到最优解的问题,为智能弹道规划提供一种新的选择。