红外探测下的拦截弹制导律辨识与弹道预报方法

张雪松,王 锋,李东泽,朱雅萌,储思思

(1.解放军信息工程大学 数据与目标工程学院,河南 郑州 450000;2.中国人民解放军32035部队,陕西 西安 710000;3.军事科学院 国防科技创新研究院,北京 100071;4.中国运载火箭技术研究院,北京 100071)

利用飞行器搭载的红外传感器对拦截弹进行探测,不仅丰富了探测手段、拓展了探测范围,同时也保证了平台的隐蔽性、增强了生存能力,对于机动突防和反拦截有着十分重要的意义[1-3]。而飞行器进行机动规避实施突防的关键是对拦截弹制导律的辨识、运动状态的估计以及后续弹道的预报。

由于红外探测器测量时仅能获得角度信息,对拦截弹定位属于不完备观测,而系统的可观性是后续制导律辨识以及运动状态估计的前提。目前,对系统可观性问题的研究较多,常用的方法有微分几何方法、数值分析方法等[4,5]。文献[6,7]采用微分几何方法对制导律辨识的非线性系统进行了可观性分析,给出了系统弱可观的充要条件。文献[8]构建了被动传感器对再入阶段弹道目标的运动参数估计模型,并基于Fisher信息矩阵对系统的可观性进行了数值验证。

根据零化视线角速率的思想,各类制导律都可以等价为不同制导律系数的比例导引[9,10],因此对制导律的辨识可以转化为对比例导引模型中制导律系数的辨识估计。文献[11-13]基于多模型自适应卡尔曼滤波算法,将制导律辨识转化为对模型的辨识,能够准确地辨识出制导律类型和制导参数,但当模型集内无匹配的制导律时,则辨识效果较差。文献[14]以飞行器和拦截弹的相对运动数据为样本输入,拦截弹制导律为标签,基于门循环单元(GRU)实现了制导律的准确辨识,但该方法未考虑双方的动力学信息,辨识的准确性有待进一步研究。

在弹道预报方面,研究的关键主要有两方面:一是获取准确的预报初值;二是建立精确的动力学模型或运动学模型。文献[15,16]采用弹道参数辨识和状态估计的思想获取预报初值,通过建立修正动力学模型,实现对弹道的预报。文献[17]通过构建深度神经网络,基于传统模型弹道数据进行训练,实现了导弹弹道的规划和快速预报,但这种方法对强机动目标效果较差。

在已有文献研究的基础上,本文采用“滤波估计—弹道预报”的思想解决红外探测条件下的拦截弹制导律辨识与弹道预报问题。首先,根据矩阵理论对系统可观性进行证明分析。在此基础上,将制导律系数增广为滤波状态分量,构造滤波器对制导律系数与运动状态进行辨识估计,并给出一种滤波稳定判断方法,将稳定收敛时刻的制导律系数及运动状态作为弹道预报初值。最后,构建拦截弹弹道预报方程,采用无迹变换的方法进行弹道预报与误差传播分析。

1 制导律辨识的可观性分析

为了便于理论分析,这里不考虑噪声的影响。设初始时刻飞行器的状态矢量为:

拦截弹的状态矢量为:

在k时刻,相对距离矢量为ΔRk,则飞行器与拦截弹的位置矢量关系为:

XMk=XIk+ΔRk

(1)

假设加速度符合指数模型,此时飞行器与拦截弹的状态矢量分别为:

(2)

(3)

式中:λi,ωi(i=x,y,z)为机动时间常数。

飞行器对拦截弹的视线方位角为βk,视线高低角为εk,则沿视线坐标系y轴的单位矢量为:

uk=(-cosβksinεkcosεksinβksinεk)T

(4)

根据矢量的正交性,由式(1)、式(4)可得:

(5)

将式(2)～式(4)代入,经过整理可以得到:

(6)

式中:

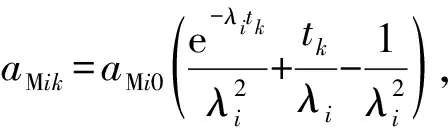
可观性即在相应的观测时段能够唯一确定系统的初值。对于式(6),等式两边左乘AT,通过观察分析可知,ATA为6×6对称矩阵,且前3行与后3行对应成比例,即Rank(ATA)=3,可知ATA不满秩。因此,对于k时刻的一次观测,式(6)没有唯一解,系统不可观。

当飞行器对拦截弹连续观测,即k=1,2…m,式(6)可以写成:

BX=C

(7)

式中:

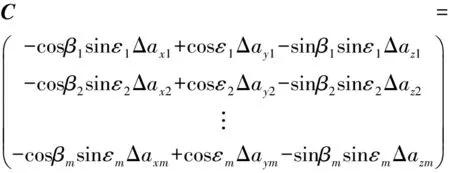
对于观测矩阵B,考虑以下几种情况:

①当视线方位角β为固定值时,矩阵B经过初等变换,有:

B→(B0Om×2)

(8)

式中:B0为m×4矩阵,Om×2为m×2零矩阵。

根据矩阵秩的定义可知,矩阵B的非零子式的最高阶小于6,即Rank(B)<6。而式(7)的状态变量维数为6,因此没有唯一解,系统不可观。

同理,对于视线高低角为固定值时,系统同样不可观。

②当视线方位角、视线高低角有变化时,对于矩阵B进行分析可知,矩阵B为列满秩,即列向量线性无关,也就是说B的零空间仅包含零向量。对于BTB来说,构造零空间BTBv=0,则有vTBTBv=0,即(Bv)TBv=0,所以Bv=0。由于v是B的零空间向量,所以BTB也是列满秩,而BTB为6×6对称矩阵,行秩等于列秩,即Rank(BTB)=6,满足唯一解条件,即系统可观。

2 制导律系数辨识模型

2.1 系统状态方程

在拦截弹的制导段,主要受到地球引力、气动力、离心力、科氏力和制导力的作用。总加速度a由以下几项组成,包括引力加速度ag、制导力加速度as,气动力加速度aA、离心力加速度acf和科氏力加速度aco,即a=ag+as+aA+acf+aco。

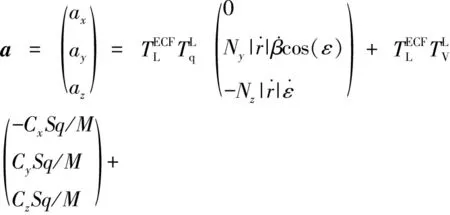
(9)

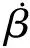
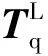
(10)

式中:φ、ψ、γ分别为俯仰角、偏航角和滚转角,P1、P2、P3分别为绕x、y、z旋转一定角度的方向余弦矩阵。

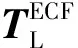
(11)

式中:ζ为发射方位角,φ为发射点的纬度,λ为发射点的经度。

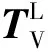
(12)

式中:ν、σ、θ分别为倾侧角、速度偏角、速度倾角。

(13)

对式(13)进行离散化处理,可以得到制导段系统状态模型。

Xk+1=ΦkXk+Ukak

(14)

式中:

其中I为单位矩阵,O为零矩阵,T为采样周期。

2.2 系统观测方程

当飞行器利用红外探测器对拦截弹进行探测跟踪时,测量数据为观测方位角ζ、观测俯仰角ξ,与拦截弹状态矢量X间的关系为:

Z(ζ,ξ)=H(X)+V

(15)

式中:V为等效测量噪声,其协方差矩阵为Cov=E(VVT),H表示拦截弹状态矢量X与观测角度的变换关系。

在地固坐标系中,设飞行器的位置矢量为(xMyMzM)T,拦截弹的位置矢量为(xIyIzI)T,则拦截弹在飞行器视场坐标系中的位置矢量为:

(16)

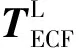
由此可以计算红外探测器的测量值为:

(17)

式(16)～式(17)构成了观测方程的解析表达式。

3 制导律系数辨识滤波器设计

3.1 过程噪声方差设计

滤波器的性能主要取决于过程噪声方差的设计,对于拦截弹的制导律系数来说,其作为制导控制指令参数通常具有非随机性和相关性,因此可以采用自相关函数为指数衰减形式的一阶Markov过程进行表示[18]。

(18)

式中:τ为机动时间常数。

将式(18)进行离散化,可以得到:

(Ni)k+1=(Ni)kexp(-T/τ)+φk

(19)

式中:φk为用于辨识制导律系数的离散化驱动白噪声,噪声方差为:

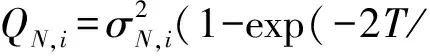
(20)

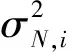
(21)

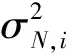
对于拦截弹的制导律系数,其取值一般为有限区间Ni∈[Nmin,Nmax],假设制导律系数在区间内满足均匀分布,则其方差为:

(22)

在制导段拦截弹一直处于机动状态,机动频率取飞行时间的倒数。

3.2 滤波算法流程

①使用式(9)计算ak/k,并进行状态预测。

(23)

②使用3.1节方法计算过程噪声方差Qk,用于补偿预测协方差矩阵。

(24)

③采用修正比例采样规则构造Sigma采样点χk+1/k(l)和相应权重Wl。

(25)

式中:n为状态向量维度,κ表示Sigma采样点的散布程度,一般取n+κ=3。

④基于观测方程的非线性传播:

Zk+1/k(l)=H[χk+1/k(l)]l=0,1,…,2n

(26)

⑤计算观测值的预估值和协方差矩阵。

(27)

⑥计算新息矢量和新息协方差矩阵。

(28)

⑦状态估计与协方差更新。

(29)

4 弹道预报与误差传播分析

4.1 预报初值确定

对拦截弹的弹道预报需要滤波结果达到稳定收敛后才能进行。对于滤波得到的数据X1,X2,X3…,从第j个数据Xj开始,依次对w个数据相邻求差的值取模

|Xj-Xj-1|=δ1
|Xj-1-Xj-2|=δ2
⋮
|Xj-w+2-Xj-w+1|=δw-1

(30)

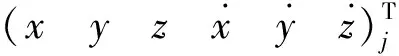
4.2 弹道预报方程

(31)

拦截弹在制导段总的加速度可由式(9)计算。同时,考虑拦截弹具有过载饱和,可以表示为:

(32)

根据滤波稳定收敛的结果,采用四阶龙格库塔积分求解微分方程得到弹道预报方程。

y=RK4[f(X),Sp,y0,h]

(33)

式中:Sp为积分区间,y0为积分初值向量,h为积分步长。

4.3 误差传播分析

由于预报初值是滤波稳定收敛时的估计值及对应的协方差,在利用有误差的估计值进行弹道预报时,会得到的一个逐渐扩散的“误差管道”,如图1所示。因此,需要对拦截弹弹道报结果进行误差传播分析。常用的分析方法有协方差描述函数法和无迹变换法,而无迹变换不需要对非线性方程线性化,精度更高[19,20],因此本文采用基于无迹变换的方法进行误差传播分析。

图1 飞行器对拦截弹探测示意图Fig.1 Diagram of aircraft detecting interceptor

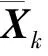
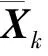
(34)

②基于式(33)的拦截弹弹道预报方程,得到sigma采样点的输出值。

γl=RK4(χl)l=0,1,…,2n

(35)

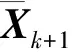
(36)

具体流程如图2所示。

图2 基于无迹变换的弹道预报流程Fig.2 Trajectory prediction process based on Unscented Transformation

5 仿真实验与结果分析

5.1 仿真场景

根据飞行器动力学方程和数值积分算法,优化一条飞行器滑翔弹道。拦截弹发射点地理坐标为19.6°E、0.4°N,高程为5 m,发射方位角为-117.65°,在发射后26.2 s进入制导段,采用比例导引方式,制导律系数为4。以飞行器飞行时间为基准,拦截弹在575.4 s发射,在601.6 s进入制导段,构建三维场景如图3所示。

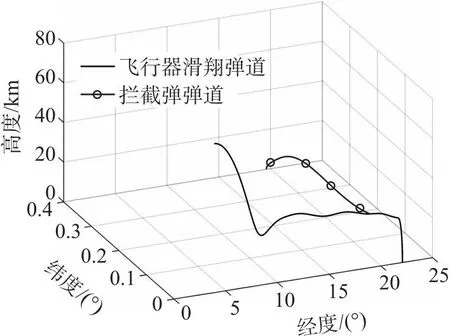
图3 三维弹道曲线Fig.3 Three-dimensional trajectory

飞行器搭载红外探测器对拦截弹进行探测跟踪,采样周期为T=0.1 s,视线方位角、视线高低角如图4所示。

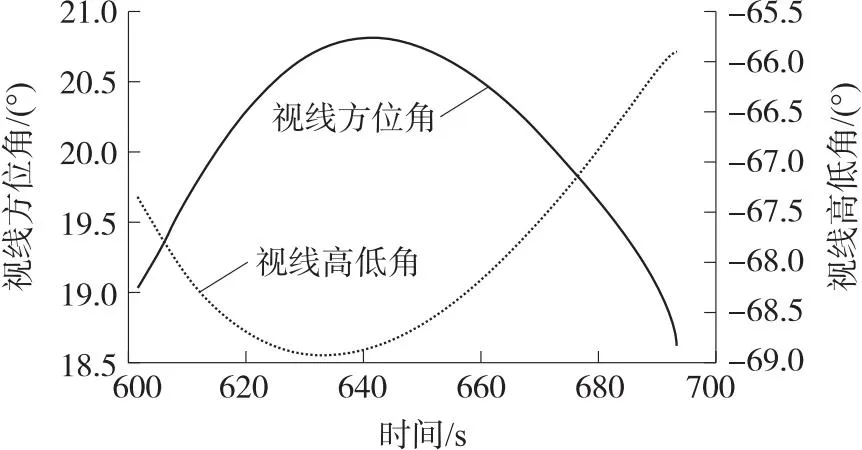
图4 视线角变化曲线Fig.4 Variation curve of line-of-sight

可以看出,视线角有较大程度的变化,根据第2节分析可知,系统是可观的。

5.2 制导律辨识

①参数设置

假设以拦截弹助推段滤波估计结束后的数据作为拦截弹初始状态矢量,制导律系数取值范围N∈[2,6],根据经验取值为3,则滤波初始估计值为:

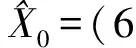
初始协方差矩阵可设为:

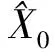
②结果分析

根据上面的参数设置,本文算法的制导律系数的辨识结果如图5所示,对比方法的制导律辨识结果如图6所示。

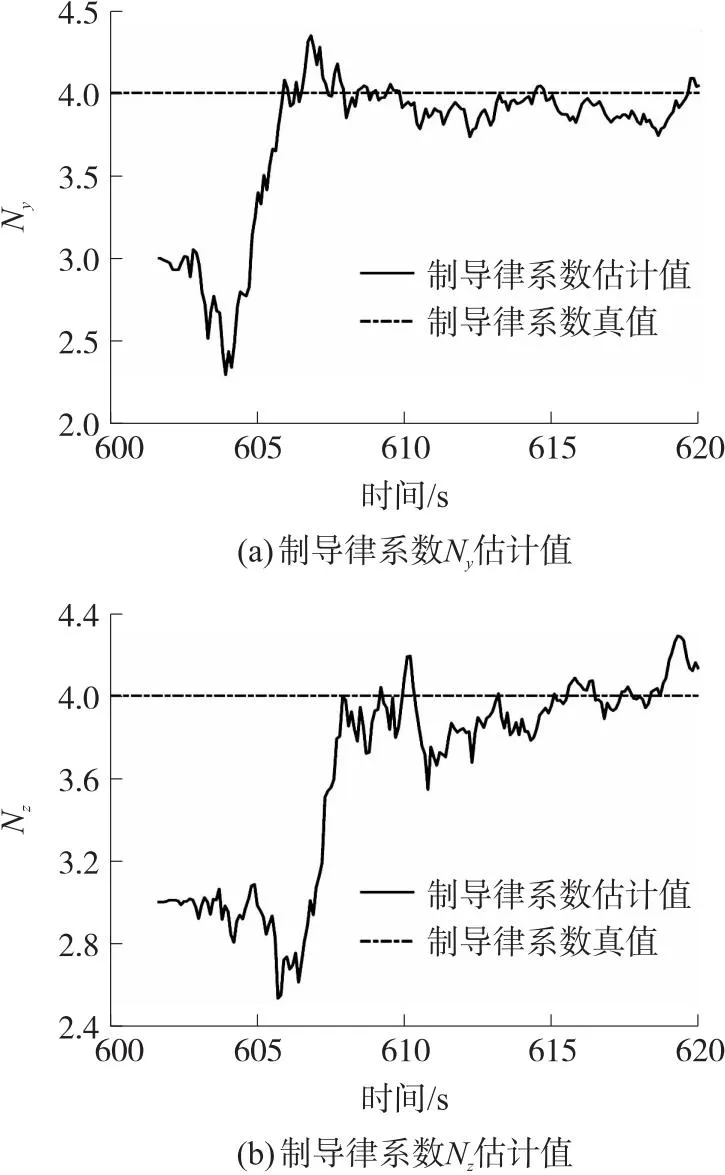
图5 拦截弹制导律系数估计值Fig.5 Estimation of guidance law coefficient for interceptor

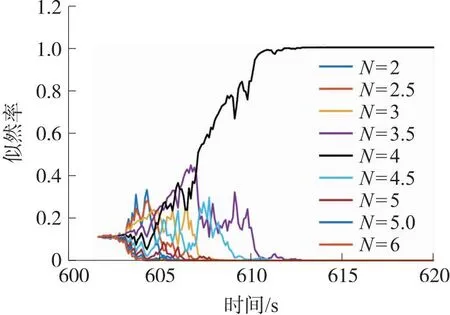
图6 对比方法的制导律辨识结果(有匹配制导律)Fig.6 The guidance law identification result of the comparison method(with matched guidance law)

从图5辨识结果可以看出,约在607 s制导律系数开始稳定收敛于真值附近,辨识结果较好,而图6中对比方法约在610 s左右辨识出制导律模型。本文算法能够直接对制导律系数实时估计,不需要构建制导律系数模型集,且辨识速度较快。而当模型集中无正确的制导律系数模型时,即N∈{2,2.5,3,3.5,4.5,5,5.5,6},辨识结果如图7所示,其辨识结果是错误的,可见该算法的辨识准确性受限于模型的数量。而本文算法解决了对比算法因模型集有限而导致的辨识估计不准确的问题,具有更强的实时性和适用性。

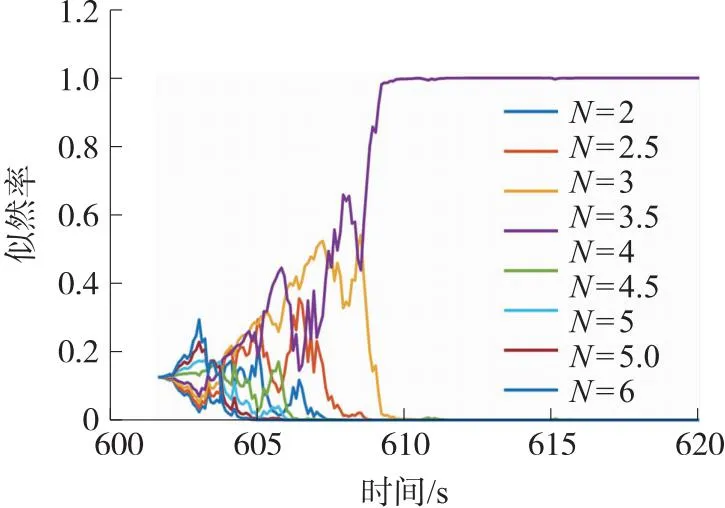
图7 对比方法的制导律辨识结果(无匹配制导律)Fig.7 The guidance law identification result of the comparison method(without matched guidance law)

对于拦截弹运动状态估计,采用均方根误差RMSE表示跟踪过程中的误差变化。以x轴方向状态估计均方根误差为例,其它方向基本相同,进行100次蒙特卡罗仿真,仿真结果如图8、图9所示。

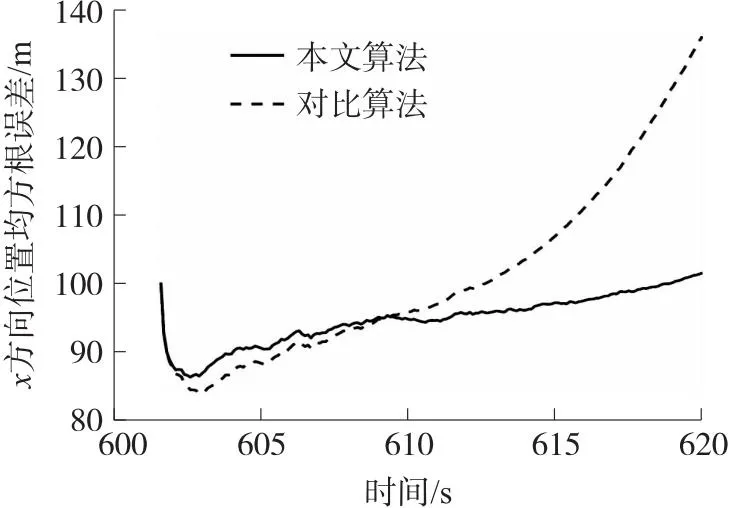
图8 x方向位置均方根误差Fig.8 RMSE of position for x-direction

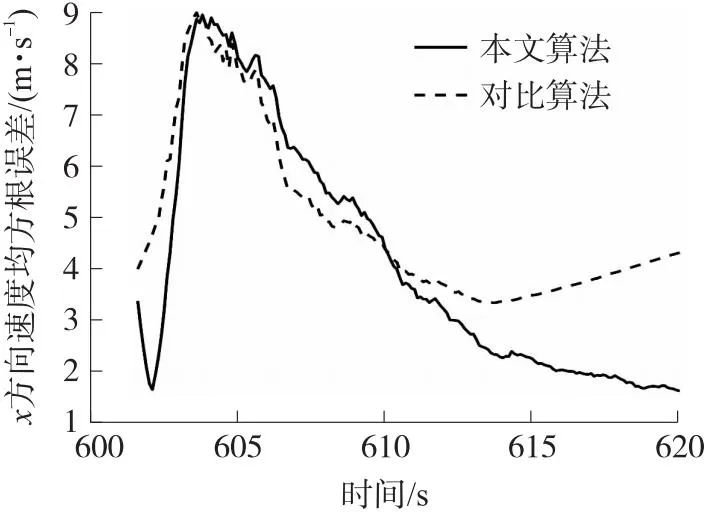
图9 x方向速度均方根误差Fig.9 RMSE of velocity for x-direction

实线描述本文算法的估计结果,虚线描述对比方法的估计结果。从图中可以看出,本文算法滤波稳定时的位置均方根误差约为95 m,而对比算法的位置均方根误差呈缓慢发散趋势;本文算法滤波稳定时的速度均方根误差约为3 m/s,而对比算法的速度均方根误差在610 s前与本文算法基本一致,而后逐渐发散。由此可见,本文算法滤波稳定性更好,对拦截弹的滤波更为稳定,且在整体上滤波估计的精度更高。

5.3 弹道预报

①参数设置

根据滤波估计得到的拦截弹制导律系数及状态估计值,采用第4节中方法进行弹道预报。滤波数据处理过程中,w=20,阈值κ=5。经计算,在607.8 s时拦截弹运动状态滤波结果整体稳定收敛,取该时刻数据作为预报初值,此时的状态估计值为:

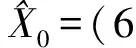
对应的估计协方差矩阵为:

对应的3σ误差椭球如图10所示。

图10 预报初始时刻误差椭球Fig.10 Error ellipsoid of initial time

②结果分析

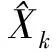
图11 弹道预报误差椭球变化曲线Fig.11 Error ellipsoid variation of trajectory prediction

由图可知,拦截弹预报初始时刻的误差椭球随着预报时间的增加而逐渐扩散,并形成了“误差管道”。而且在y方向上的预报误差增速较大,在x方向、z方向上的增速较小。由于是3σ椭球,真实的弹道将以97.3%的概率从误差椭球构成的“误差管道”穿过。

弹道预报位置的标准差与实际预报误差的变化曲线如图12所示,其中虚线表示弹道预报的标准差,实线表示弹道预报的实际误差。

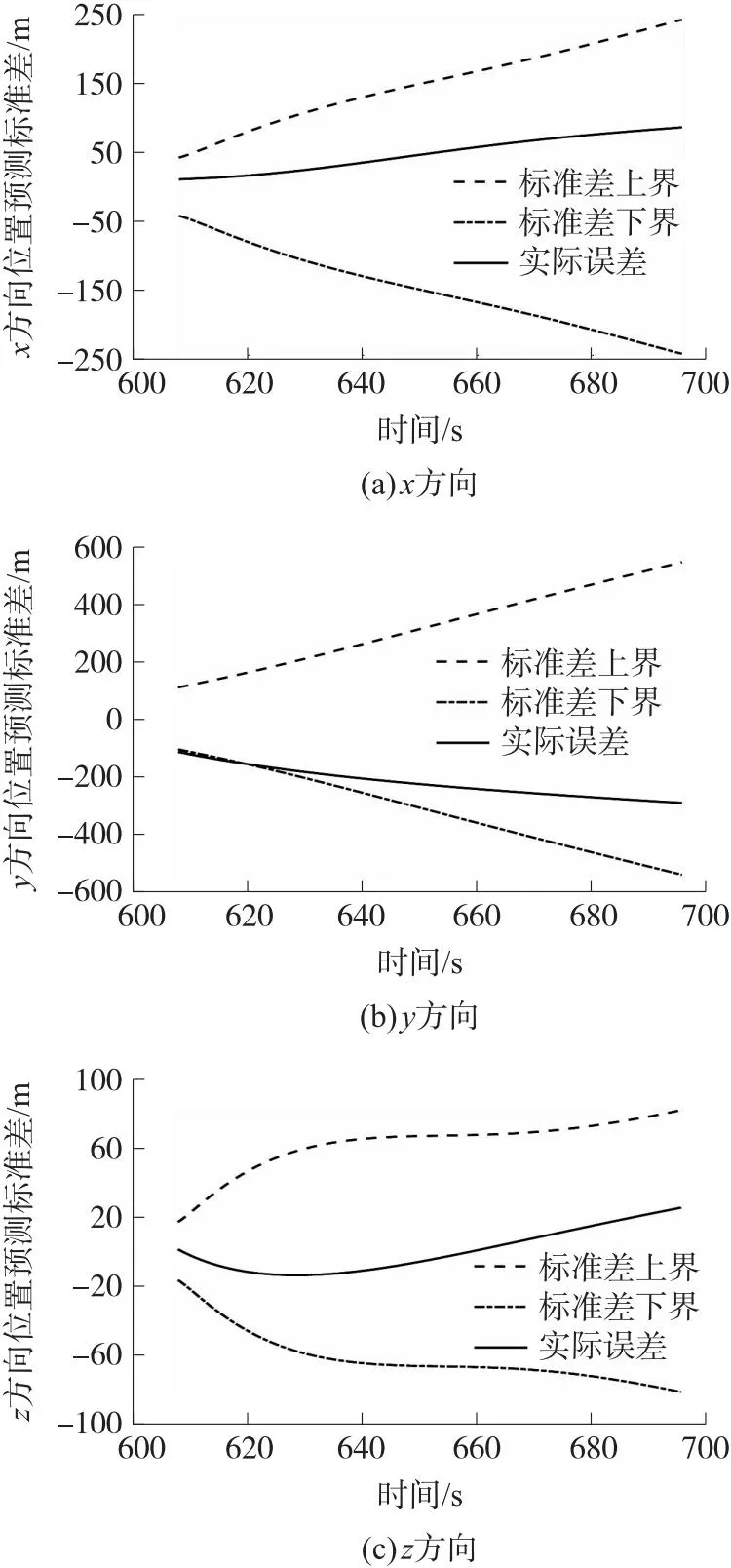
图12 弹道预报标准差与实际误差曲线Fig.12 Trajectory prediction standard deviation and actual error

由图可知:各方向弹道预报的实际误差基本落在标准差范围内,y方向弹道预报的实际误差在起始阶段低于误差标准差下界,这是因为在“滤波估计—弹道预报”过程中,滤波稳定收敛时,在y方向拦截弹位置估计误差大于其他两个方向。在整个预报过程中,随着预报时刻的推移,各方向实际误差的变化趋势与标准差相符,位置误差均不断累积,呈发散趋势,但整体均在标准差范围内。在预报终止时刻,x方向实际误差为85 m,预报标准差为240.7 m;y方向实际误差为292.6 m,预报标准差为537.5 m;z方向实际误差为25 m,预报标准差为80 m,总体来说弹道预报效果较好。

通过分析可知,引入无迹变换的弹道预报算法能够实现拦截弹弹道的准确预报,并且能够给出弹道预报的误差范围,但弹道预报的精度主要取决于对拦截弹制导律系数与运动状态的估计精度。

6 结论

本文针对红外探测下的拦截弹制导率辨识与弹道预报问题,主要做了以下工作:一是分析了在仅有角度测量信息的条件下,系统的可观性取决于飞行器与拦截弹的观测角变化情况;二是将制导律系数增广为滤波状态分量,提出一种过程噪声自适应的无迹卡尔曼滤波算法,实现了对拦截弹制导律系数与运动状态的准确估计;三是采用无迹变换的方法对拦截弹的弹道进行预报和误差传播分析。仿真结果表明,本文提出的算法是有效的,对制导律系数和运动状态的辨识与估计在收敛速度和精度上能够满足后续计算要求,同时对弹道预报的结果能够为飞行器机动突防和规避拦截提供理论支撑。