基于光幕阵列的近炸引信炸点坐标测量方法

2024-01-05王佳,杨帅,董涛

弹道学报 2023年4期

王佳,杨帅,董涛

(1.西安工业大学科学技术研究院,陕西西安 710032;2.西安机电信息技术研究所机电动态控制重点实验室,陕西西安 710065;3.西安工业大学光电工程学院,陕西西安 710032)

在对近炸引信近炸距离参数进行试验测量时,无论带有近炸引信的弹丸是否爆炸,安装有引信的弹丸和被毁伤目标的相对位置是判定引信近炸距离合格与否的一个重要依据[1,2]。近炸引信在离目标较近的距离爆炸,靠弹丸形成的破片和冲击毁伤目标[3]。当被攻击目标在空间内的位置固定时,只需要测得装有引信的弹丸爆炸点在三维空间内的坐标,即可得到引信作用时的炸点位置与被攻击目标之间的距离。所以实现近炸引信弹丸的炸点坐标和空间飞行弹道轨迹的精确测量,对近炸引信的研制和试验评估具有重要意义。

现阶段在兵器靶场测试中对近炸引信空间炸点三维坐标测量的常用方法主要包括声阵列测量法[4-6]、双CCD交汇测量法[7-9]和多光幕阵列测量法[10-12]。声阵列测量法采用多个声传感器组成声阵列测量系统,声阵列采集弹丸爆炸产生的声波,测量系统提取爆炸声波到达各个传感器的时间差来计算出炸点位置,但该方法容易受到高速飞行弹丸产生的激波影响造成误触发且无法探测未爆炸弹丸的位置信息。双CCD交汇测量法采用双CCD相机作为探测器,两台相机视场交汇布置,使相机的视场包含目标位置,两台相机捕捉到弹丸爆炸时产生的火光,通过相机布置参数及靶机的位置参数,计算得到炸点坐标。该方法同样无法探测未爆炸弹丸的坐标,且对相机的精度和分辨率要求较高,成本较大。文献[12-14]采用的四光幕阵列及圆形阵列测量方法仅可用来测量飞行弹丸的着靶坐标,无法测量弹丸的炸点坐标。文献[15]采用六光幕阵列进行环形布阵,实现对静爆破弹丸破片在任意水平方向速度的测量,但无法得到弹丸的炸点坐标。文献[10]采用四光幕靶及闪光靶对弹丸炸点坐标进行测量,虽然可以测量得到弹丸的炸点坐标,但无法得到弹丸飞行过程中的其他参数。文献[11]在四光幕的基础上额外增加光幕,构建六光幕阵列,配合炸点火焰探测器,同时可以实现对理想条件下呈直线飞行状态弹丸的速度、飞行俯仰角、方位角以及炸点坐标的测量。但是考虑到实际试验时,弹道的区截距离较长,弹丸在飞行过程中会受到重力和空气阻力的影响速度逐渐衰减,此时弹丸的运动轨迹呈曲线,在终点弹道段弹丸的散布区域就会增大[16,17]。继续使用理想情况下的直线测量模型就会产生较大的测量误差。

针对现有弹丸空间炸点三维坐标测量系统和方法存在的不足,本文提出一种基于多光幕阵列配合火焰探测原理的曲线运动弹丸空间炸点三维坐标测量方法,采用2台“N”形三光幕探测器和1台单光幕探测器组成7光幕阵列,配合炸点火焰探测器构建测量系统主探测单元,建立弹丸炸点坐标测量数学模型,并对炸点坐标测量误差进行分析、仿真和实验验证。

1 光幕探测原理

光幕探测原理如图1所示,单光幕探测器以天空为背景,由于光阑狭缝的限制,进入光学镜头的光线为有一定厚度的扇形,称之为探测光幕。当弹丸等高速飞行物体穿过该光幕时,遮挡了进入光阑狭缝的部分光线,此时通过狭缝到达光电转换器件接收面的光通量就会发生变化,信号处理电路就会产生一个对应弹丸穿过光幕时刻的脉冲信号[18]。

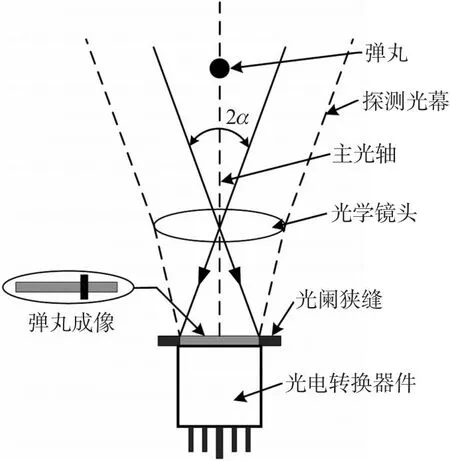
图1 光幕探测原理示意图Fig.1 Schematic diagram of light screen detection principle

对于图1所示的单光幕探测系统,一般情况下镜头焦距越短,其探测视场角越大,但系统的通光孔径会随之减小,进而使得系统的探测灵敏度降低。因此,为了兼顾系统探测灵敏度和探测视场角,本文采用了如图2所示的双镜头拼接扩展扇形探测视场的方法,每2个镜头为一组形成一道探测光幕,单只镜头焦距为50 mm,配合有效光敏面为30 mm的光电管形成30°的扇形探测视场,2个镜头拼接可形成60°的扇形探测光幕。图2(a)为三光幕探测器的俯视图,中间光幕与两侧光幕的夹角在水平面内为α。图2(b)为三光幕探测器的主视图,两侧探测光幕与中间光幕任一镜头主光轴的角度为β。由以上光机结构固定三组光学镜头,便可以在空间形成“N”形探测幕面。

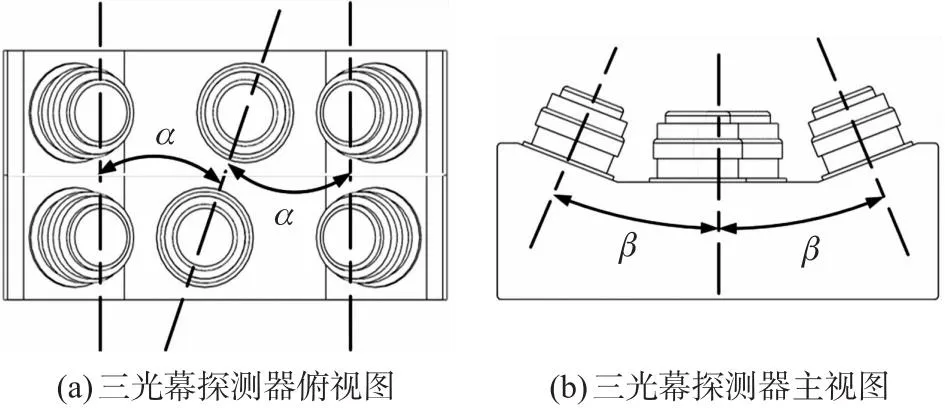
图2 三光幕探测器结构示意图Fig.2 Schematic diagram of three-light screen detection structure

炸点火焰探测器使用有效探测面为圆形的光电转换器件,配合光学镜头在空间形成锥形的探测视场。当弹丸在炸点火焰探测器的视场内爆炸,光电转换器件探测到爆炸产生的火光,相应的处理电路便会产生与弹丸爆炸时刻对应的脉冲信号[19]。

2 系统探测原理

2.1 多光幕阵列探测系统布置方案

图3为基于多光幕阵列配合火焰探测原理的弹丸空间炸点三维坐标测量系统总体组成示意图。沿预定弹道线间隔一定距离分别放置2台三光幕探测器,分别为启动探测器与截止探测器,在2台三光幕探测器中间放置1台单光幕探测器,称之为中间探测器,构建7光幕阵列,并且在截止探测器末端一定距离沿弹道线放置1台炸点火焰探测器。

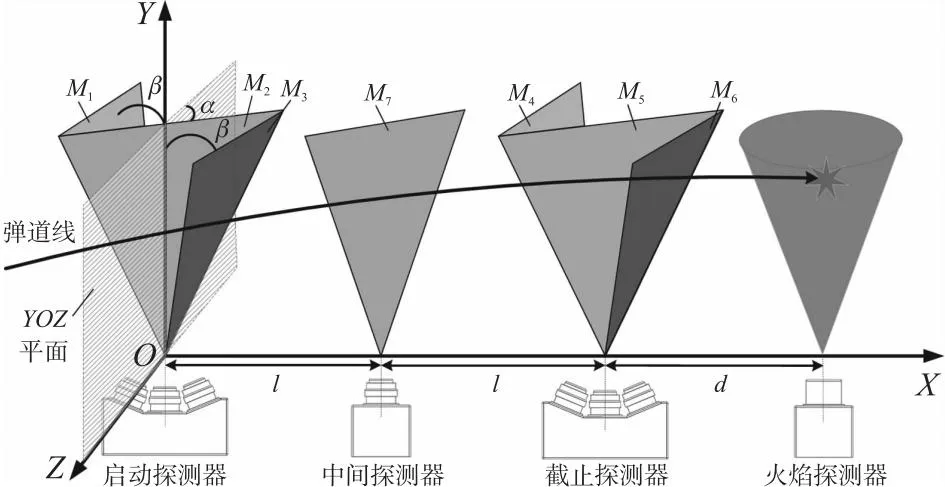
图3 测量系统组成示意图Fig.3 Measurement system composition diagram

当带有近炸引信的飞行弹丸依次穿过探测系统的7道探测光幕Mi(i=1～7),7道探测光幕对应的处理电路依次输出7个弹丸信号,经弹丸信号采集处理仪采集,通过弹丸过幕时刻提取算法计算[20,21],得到弹丸穿过7个探测光幕的时刻值ti(i=1～7),进一步根据系统光幕阵列的空间位置参数构建弹丸运动方程。当飞行弹丸在炸点火焰探测器的探测视场内爆炸时,炸点火焰探测器探测到弹丸爆炸产生的火焰信号并输出对应爆炸时刻的脉冲信号,经处理后得到弹丸穿过YOZ平面到爆炸点的时间间隔TB,将该时间间隔代入弹丸运动方程获得炸点坐标。

当弹丸没有发生爆炸时,系统可得到弹丸穿过7道探测光幕的着靶坐标和速度。

2.2 构建多光幕阵列平面方程

根据外弹道学以及实际测量环境下的测试需求,建立空间三维笛卡尔测量坐标系。以第1个“N”形光幕中3个探测光幕的交点为坐标原点O,预定弹道线方向为X轴,Y轴垂直水平面向上,依据右手定则确定Z轴。2台三光幕探测器布置于预定弹道线下方,2台三光幕探测器距离为S,单光幕探测器放置于2台三光幕探测器的中间位置,其与2台三光幕探测器的距离均为l,2台三光幕探测器的垂直距离为h(以截止探测器高为正,则h>0,否则h<0),炸点火焰探测器到截止探测器的距离为d。根据图2三光幕探测器的结构参数及图3所建三维坐标系,对启动探测器进行分析可知:光幕M1,M3与YOZ平面的夹角为β,光幕M2与YOZ平面的夹角为α。因截止探测器与启动探测器完全相同,所以上述的结构参数也相同,光幕M1与M4相互平行,M3与M6相互平行,光幕M2,M7,M5相互平行。

根据以上7个探测光幕的空间位置关系,可建立光幕M1～M6的空间平面方程:

(1)

整理成为矩阵形式为:

(2)

2.3 阻力加速度测量公式

当弹丸处于末端弹道,特别是在长区截弹道时,受到重力、空气阻力以及其他因素影响,弹丸飞行速度低,散布区域大,弹丸运动轨迹呈曲线状态。此时,外部作用力产生的影响已不可忽略。根据外弹道学及空气动力学分析,重力对弹丸运动的影响始终向下,空气阻力对弹丸做质心运动时速度大小和方向的影响与阻力加速度a有关[16,17]。弹丸在空气中运动时空气阻力加速度a的矢量方向始终与弹丸的质心速度矢量方向相反。

如图4所示,预定弹道O1与XOZ平面平行,光幕M2,M7和M5相互平行且都垂直于平面XOZ,并且与Z轴成一定的角度α(α<90°),光幕M2,M7与弹道线交点的距离,光幕M7,M5与弹道线交点的距离均为l,则S1=lcosα。弹丸穿过光幕的时刻值分别为t2,t7,t5。则可求得弹丸在X轴的阻力加速度ax:

(3)

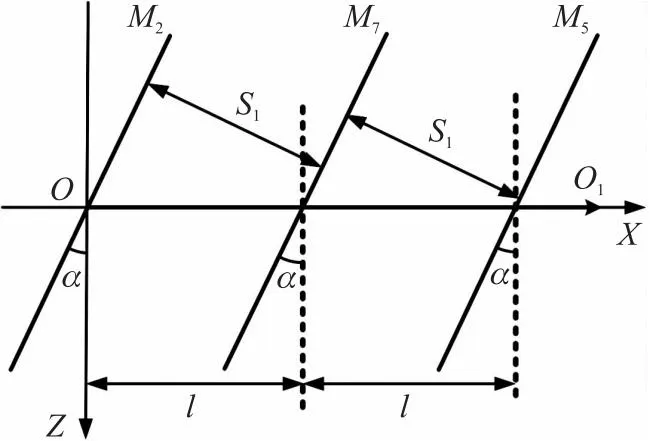
图4 加速度测速原理图Fig.4 Schematic diagram of acceleration speed measurement

(4)

(5)

2.4 炸点坐标测量公式

弹丸在飞行过程中可视为做质心运动,弹丸的速度矢量沿预定弹道线方向,加速度的矢量方向与弹丸质心速度矢量共线相反,重力加速度g对弹丸的影响始终垂直向下。假设弹丸穿过光幕M1时的坐标为(x1,y1,z1),穿过光幕M1时弹丸速度在XOZ平面上的投影为(vx1,vy1,vz1)。测量得到弹丸穿过7个光幕的时刻ti(i=1～7)以及弹丸穿过全部探测光幕后到达炸点火焰探测器探测视场爆炸的时刻值TB,其中t1=0,为参考零时刻。根据运动学方程便可得到弹丸在空间中做曲线运动的数学表达式,结合弹丸穿过6个探测光幕的时间,便可计算得到弹丸飞行时的运动轨迹和穿过剩下5个探测光幕的坐标和瞬时速度的投影,则弹丸穿过所有探测光幕时的空间曲线运动方程如下:

(6)

通过式(6)计算出弹丸穿过剩下5道探测光幕时的坐标和瞬时速度,并将6个坐标和对应的瞬时速度依次代入式(2)并整理为矩阵形式,可得:

A·C=B

(7)

式中:

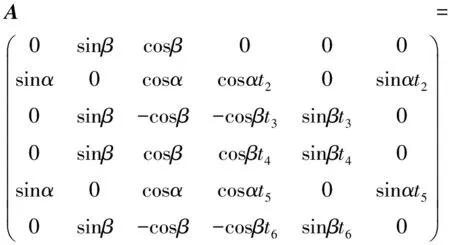
因此有:

C=A-1·B

(8)

将三光幕探测器的结构参数角度α,β,两探测器的间距S,两探测器的高度差h,弹丸依次穿过探测光幕的时刻值ti以及式(5)所解出的阻力加速度分量ax代入式(8),即可计算得到弹丸的坐标和速度。

弹丸速度矢量V在穿过第一道探测光幕时空间三维坐标系中的方向如图5所示,其中,速度矢量与XOZ水平面的夹角为俯仰角θ;速度矢量在XOZ平面上的投影与XOY平面的夹角为方位角γ。

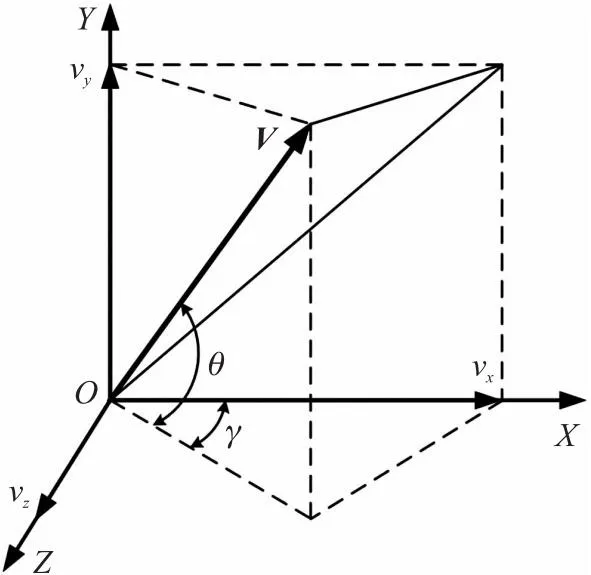
图5 弹丸速度矢量方位图Fig.5 Projectile velocity vector azimuth map

则有:

(9)

(10)

(11)

将式(8)计算得到的(x1,y1,z1)以及(vx1,vy1,vz1)代入式(9)～式(11)便可得到弹丸的飞行速度,飞行速度方向的俯仰角和方位角。

已知弹丸穿过YOZ平面到达爆炸点的时刻为TB,则弹丸炸点坐标(X,Y,Z)为:

(12)

(13)

Z=z1+vz1TB

(14)

3 炸点坐标测量误差仿真分析

由式(12)～式(14)可知,炸点坐标是弹丸穿过光幕M1时的着靶坐标、速度、重力加速度和爆炸时间的函数。炸点坐标X,Y,Z的测量误差分别为ΔX,ΔY,ΔZ,由误差传递理论,即:

(15)

(16)

(17)

设置仿真条件:假定vz1取4 m/s,vy1取5 m/s,vx1取值在0 m/s到200 m/s区间变化,速度的测量误差取0.4 m/s;位置的测量误差取5 mm;TB取值在0 ms到20 ms区间变化,炸点时间TB测量误差取6 μs;ax的测量误差为1 m/s2;考虑到实验地点海拔高度变化不大,因此g的测量误差忽略不计。则炸点坐标的误差分布规律如图6所示。

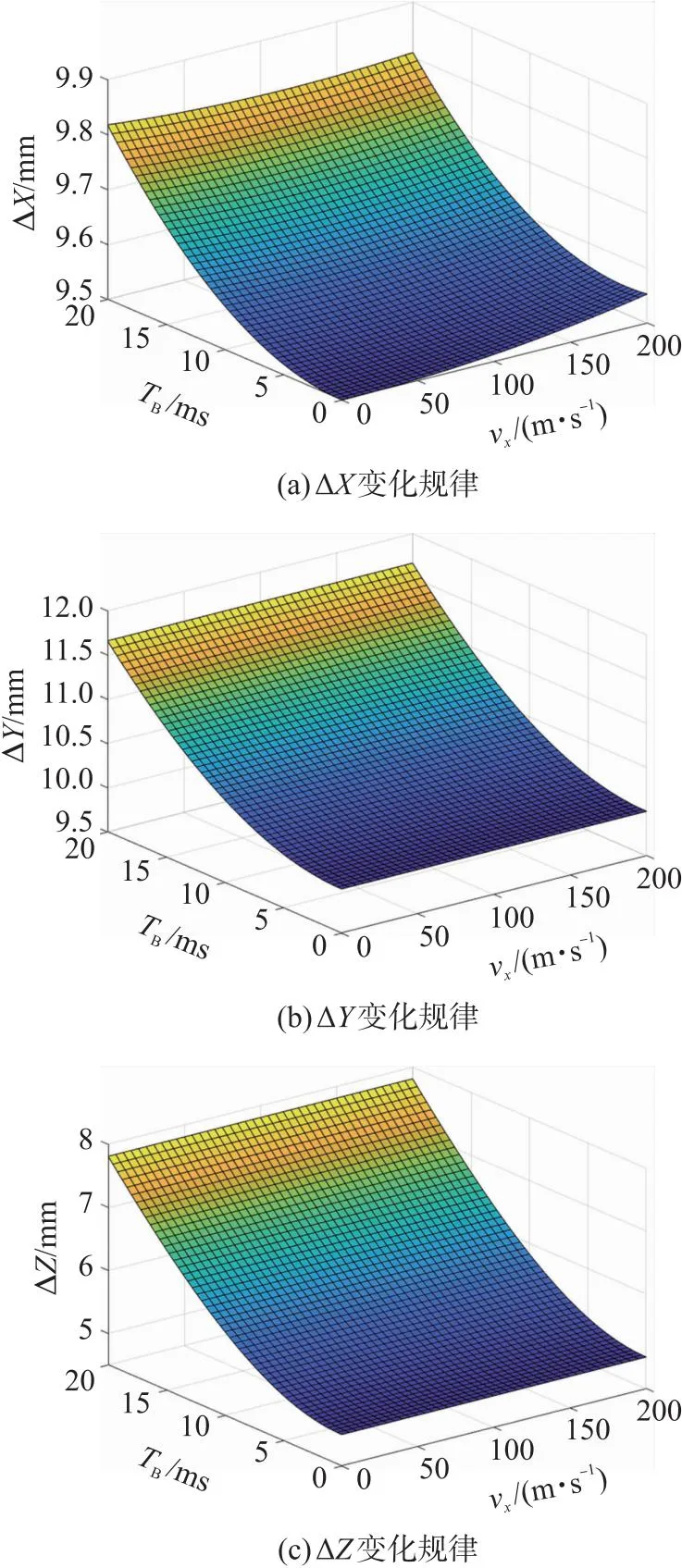
图6 炸点坐标误差变化规律Fig.6 Variations of explosion point coordinates error

由图6可看出,炸点坐标X的测量误差同时受到TB和vx的影响,且随着爆炸时间TB和vx的增加而增加,ΔX最大为9.817 mm;炸点坐标Y、Z的测量误差ΔY、ΔZ随着爆炸时间TB和vx的增加而增加,但是ΔY、ΔZ受vx的影响很小。ΔY最大为11.66 mm,ΔZ最大为7.81 mm。

令TB为20 ms,ΔX受vx的影响如图7所示。

图7 ΔX随vx变化规律示意图Fig.7 Variations of ΔX along with vx

由图7可以看出当TB为20 ms时,vx从100 m/s变化至120 m/s时,ΔX呈逐渐减小趋势,最小不超过8.354 mm,但是vx从120 m/s到200 m/s变化时,ΔX呈逐渐增大趋势,最大不超过9.809 mm。

4 实验验证

为了验证上述测量系统的误差结果,按照图8所示搭建7光幕阵列配合炸点火焰探测器的炸点坐标测量系统,炸点火焰探测器使用单光幕探测器替代,使用弹丸穿过单光幕探测器时的触发信号模拟弹丸爆炸时产生的触发信号。启动探测器与截止探测器的距离S=3 992 mm,两探测器高度差为20 mm,中间探测器位于2台三光幕阵列探测器中间位置,单光幕探测器距离截止探测器1 115 mm,纸靶置于截止探测器后方2 000 mm。采用一台8通道数据采集仪,采集弹丸穿过每个探测光幕时对应处理电路输出的弹丸模拟信号,以及使用单光幕探测器模拟的弹丸在炸点火焰探测器视场内爆炸时炸点火焰探测器电路输出的炸点模拟信号,并通过相关算法计算得到弹丸穿过每个探测光幕对应的时刻值及弹丸炸点时刻值。最后通过式(9)～式(11)求解出弹丸的飞行速度、俯仰角和方位角,通过式(12)～式(14)求解出弹丸的空间炸点坐标。使用气枪发射直径为7 mm的钢珠弹进行实验,将弹丸穿过所有探测光幕的时刻值和模拟炸点时刻值分别代入文献[11]中提出的直线测量模型和本文提出的测量模型。首先计算出两种模型的坐标与纸板靶坐标的相对误差,然后通过相对误差求解得到各坐标的测量误差,得到的两种模型的部分实验数据如表1所示。

表1 部分弹丸炸点坐标实验数据Table 1 Partial projectile explosion coordinate measurement data

图8 实验布局示意图Fig.8 Schematic diagram of the test layout

由表1中的数据可以看出,本文测量模型计算得到的炸点坐标测量误差均小于直线测量模型计算得到的炸点坐标测量误差。本文方法得出的炸点坐标测量误差绝对值最大(8.4 mm,8.2 mm,5.9 mm)。由此可以计算得到炸点坐标误差的标准差σx、σy、σz分别为2.89 mm、4.97 mm、2.19 mm。仿真与实弹实验数据结果表明,本文所提出的测量方法和系统具有可行性,且坐标测量误差均优于直线测量模型,可以实现对近炸引信弹丸炸点三维坐标的测量。