核心素养立意下的函数与导数命题
2024-01-04周建锋
周建锋

1 命题
原创题已知函数f(x)=ex-1-ln x(其中e=2.718 28……是自然对数的底数),过点(a,b)(a≠0)可作曲线f(x)的两条切线.
(1)请给出a,b应满足的充要条件;
(2)求证:b<2ea-1-2ln |a|-12a2+a-32.
(参考数据:e≈1.65.)
考查目标:重点考查学生综合运用函数和导数解决实际问题的能力,以及对新情境问题分析理解的能力.
设计思路:近几年全国及各地高考数学卷对极值点偏移问题考查得比较多,广大师生对这类题的研究比较深入,难以考查出学生的实际能力.2022年全国Ⅰ卷别出心裁,考查交点问题并证明三个交点横坐标成等差数列,体现出推陈出新的导向.
本题融入切线问题,考查学生对切线问题的分析能力.f(x)是一个下凸函数,过某些平面区域的点可作两条切线,过某些平面区域的点可作一条切线,过某些平面区域的点没有切线,这需要学生进行深入分析,并作出严谨的论述.得到a,b应满足的充要条件后,第(2)问设计了一个不等式,需要利用第(1)问的结论,将不等式进行优化,而且优化后直接证明也有难度,需要用放缩或分析隐零点等手段进一步证明.
2 命题过程
原始题已知函数f(x)=ex-1-ln x(其中e=2.718 28……是自然对数的底数).
(1)求f(x)的最小值;
(2)若过点(a,b)(a≠0)可作曲线f(x)的两条切线,求证:a+b-2f(a)<115+ln 2.
(参考数据:ln 2≈0.693 1,ln 3≈1.098 6,ln 5≈1.609 4.)
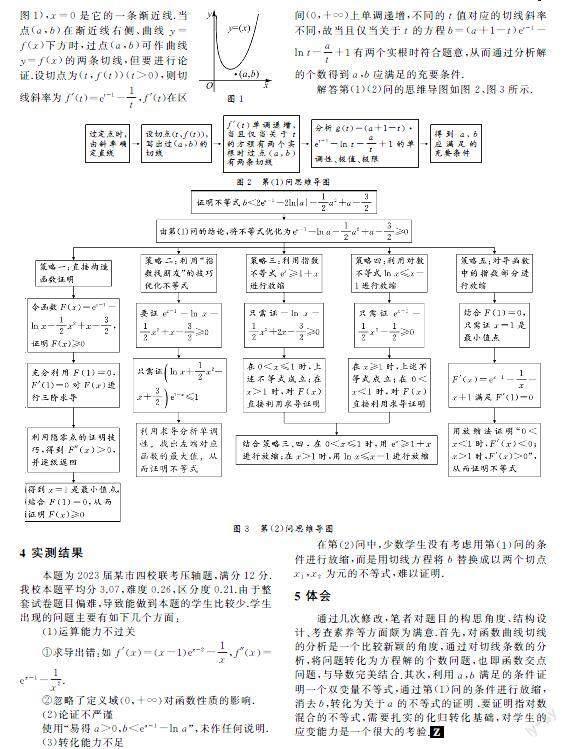
说明:命题的最初想法就是角度新一些,从分析过一点作函数曲线的两条切线,得到a,b应满足的充要条件a>0,b 修改1已知函数f(x)=ex-1-ln x(其中e=2.718 28……是自然对数的底数). (1)求f(x)的最小值; (2)若过点(a,b)(a≠0)可作曲线f(x)的两条切线,求证:b<2f(a)-a2+2a-1. (参考数据:ln 2≈0.693 1,ln 3≈1.098 6,ln 5≈1.609 4.) 说明:通过这次修改,第(2)问需要证明一个复杂的不等式ex-1-ln x-x2+2x-1>0,但可以通过第(1)问的结论,放缩为-x2+2x>0在0 修改2已知函数f(x)=ex-1-ln x(其中e=2.718 28……是自然对数的底数). (1)求f(x)的最小值; (2)若过点(a,b)(a≠0)可作曲线f(x)的两条切线,求证:b<2ea-1-2ln |a|-a2+2a-54. (參考数据:ln 2≈0.693 1,ln 3≈1.098 6,ln 5≈1.609 4.) 说明:解决了修改2的两个问题后,题目已经比较完善了,但又觉得第(1)问与第(2)问没有关联性,显得别扭(仅仅为了给学生送几分而已),故修改为删去第(1)问,把第(2)问分割成两个问题. 修改3已知函数f(x)=ex-1-ln x(其中e=2.718 28……是自然对数的底数),过点(a,b)(a≠0)可作曲线f(x)的两条切线. (1)请给出a,b应满足的充要条件; (2)求证:b<2ea-1-2ln |a|-a2+2a-54. (参考数据:ln 2≈0.693 1,ln 3≈1.098 6,ln 5≈1.609 4.) 说明:到第四稿,还是觉得第(2)问的结构不是很完美,证明过程中过多地用到一些特殊数据,所以再次修改,得到最终稿,即本文开头的原创题. 3 试题分析 第(1)问分析:对f(x)求导,f′(x)=ex-1-1x, f″(x)=ex-1+1x2>0,发现f(x)是一个下凸函数(如图1),x=0是它的一条渐近线.当点(a,b)在渐近线右侧、曲线y=f(x)下方时,过点(a,b)可作曲线y=f(x)的两条切线,但要进行论证.设切点为(t,f(t))(t>0),则切线斜率为f′(t)=et-1-1t,f′(t)在区间(0,+∞)上单调递增,不同的t值对应的切线斜率不同,故当且仅当关于t的方程b=(a+1-t)et-1-ln t-at+1有两个实根时符合题意,从而通过分析解的个数得到a,b应满足的充要条件. 解答第(1)(2)问的思维导图如图 2、图3所示. 4 实测结果 本题为2023届某市四校联考压轴题,满分12分.我校本题平均分3.07,难度0.26,区分度0.21.由于整套试卷题目偏难,导致能做到本题的学生比较少.学生出现的问题主要有如下几个方面: (1)运算能力不过关 ①求导出错:如f′(x)=(x-1)ex-2-1x,f″(x)=ex-1-1x2. ②忽略了定义域(0,+∞)对函数性质的影响. (2)论证不严谨 使用“易得a>0,b (3)转化能力不足 在第(2)问中,少数学生没有考虑用第(1)问的条件进行放缩,而是用切线方程将b替换成以两个切点x1,x2为元的不等式,难以证明. 5 体会 通过几次修改,笔者对题目的构思角度、结构设计、考查素养等方面颇为满意.首先,对函数曲线切线的分析是一个比较新颖的角度,通过对切线条数的分析,将问题转化为方程解的个数问题,也即函数交点问题,与导数完美结合.其次,利用a,b满足的条件证明一个双变量不等式,通过第(1)问的条件进行放缩,消去b,转化为关于a的不等式的证明 .要证明指对数混合的不等式,需要扎实的化归转化基础,对学生的应变能力是一个很大的考验.
