聚焦椭圆与三角溯源算理与算法

余泳 吴宣良 武星红

1 问题再现

（2023年全国高考数学甲卷理科第12题）已知椭圆x29+y26=1，F1，F2为两个焦点，O为原点，P为椭圆上一点，cos∠F1PF2=35，则|OP|=（）.

A.25

B.302

C.35

D.352

2 问题分析

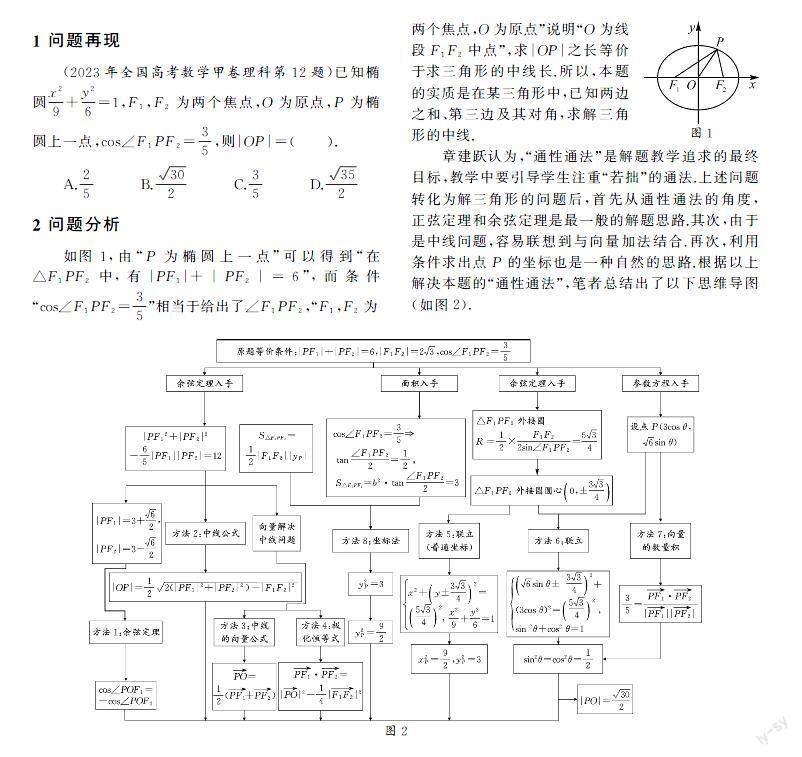
如图1，由“P为椭圆上一点”可以得到“在△F1PF2中，有|PF1|+|PF2|=6”，而条件“cos∠F1PF2=35”相当于给出了∠F1PF2，“F1，F2为

两个焦点，O为原点”说明“O为线段F1F2中点”，求|OP|之长等价于求三角形的中线长.所以，本题的实质是在某三角形中，已知两边之和、第三边及其对角，求解三角形的中线.

章建跃认为，“通性通法”是解题教学追求的最终目标，教学中要引导学生注重“若拙”的通法.上述问题转化为解三角形的问题后，首先从通性通法的角度，正弦定理和余弦定理是最一般的解题思路.其次，由于是中线问题，容易联想到与向量加法结合.再次，利用条件求出点P的坐标也是一种自然的思路.根据以上解决本题的“通性通法”，笔者总结出了以下思维导图（如图2）.

3 问题解决

余弦定理思路：利用椭圆的定义以及余弦定理直接求出|PF1|，|PF2|，再利用余弦定理列方程求出|PO|的值，得到方法1.

方法1：在△F1PF2中，由cos∠F1PF2=35，得

|PF1|2+|PF2|2－65|PF1||PF2|=12.①

由题可得

|PF1|+|PF2|=2a=6.②

联立①②得|PF1|=3+62，|PF2|=3-62.

又cos∠POF1=－cos∠POF2，|OF1|=|OF2|=3，所以可得

|PO|2+|F1O|2－|PF1|22|PO||F1O|

=－|PO|2+|F2O|2－|PF2|22|PO||F2O|.

解得|PO|=302.

人教A版新教材必修二课后习题中给出了中线公式，学生可以直接利用椭圆的定义以及余弦定理求出|PF1|2+|PF2|2，再由中线公式求解，得到方法2.

方法2：同方法1得到①②，联立得

|PF1|2+|PF2|2=21，|PF1|＼5|PF2|=152.

由中线公式，知|F1F2|=23，解得|PO|=302.

事实上，中线公式可以由向量推导而来，因此求出|PF1||PF2|，|PF1|2+|PF2|2后，结合中线的向量公式以及数量积即可求出|OP|，于是得到方法3.

方法3：由PO=12（PF1+PF2），得|OP|=|PO|=12|PF1+PF2|

=12|PF1|2+2PF1·PF2+|PF2|2=21+2×35×152=302.所以|PO|=302.

在利用向量考慮中线问题时，极化恒等式是常用思路之一，这里求出|PF1||PF2|后可以利用极化恒等式求解，于是得到方法4.

方法4：由极化恒等式PF1·PF2=|PO|2－14|F1F2|2，得|PO|=PF1·PF2+14|F1F2|2.又|F1F2|=23，解得|PO|=302.

正弦定理思路：本题直接利用正弦定理会遇到困难，因为|PF1|与|PF2|的长度未知.但由|F1F2|=23，cos∠F1PF2=35，可知|F1F2|与∠F1PF2是定值，因此由正弦定理可以求解三角形外接圆半径和确定外接圆圆心的位置.点P可以看作是圆弧与椭圆的交点，进而求出点P坐标.

假设点P的坐标为（x0，y0），联立椭圆方程与圆弧方程求解（x0，y0），于是得到方法5.

方法5：由|F1F2|=23，cos∠F1PF2=45，可知点P的轨迹是两段圆弧，其半径为|F1F2|2sin∠F1PF2=534，圆心O1，O2在y轴上且与原点的距离为|F1F2|2＼5|cot∠F1PF2|=334.所以，两段圆弧所在圆的方程为x2+y±3342=7516，结合椭圆方程得P（x0，y0）满足x0=±322，y0=±3.故|OP|=302.

利用参数方程可以避免联立椭圆与圆弧所在圆的方程，设点P的坐标为（3cos θ，6sin θ），联立圆弧所在圆的方程求解即可，得到方法6（略）.

求解坐标思路：根据题目条件建立方程求解点P的坐标也是较为通用的思路，利用参数方程和向量可以求解，得到方法7.

方法7：设点P的坐标为（3cos θ，6sin θ），则PF1=（－3－3cos θ，－6sin θ），PF2=（3－3cos θ，－6sin θ）.由35=PF1·PF2|PF1||PF2|，化简可得2cos 4θ+13cos 2θ－7=0.解得cos 2θ=12，故sin 2θ=12.因此|OP|=9cos 2θ+6sin 2θ=302.

焦点三角形面积公式是常用的二级结论之一，根据焦点三角形面积公式求出△F1PF2的面积，即可得到点P的坐标，得到方法8.

方法8：设∠F1PF2=2θ，0<θ<π2，所以S△F1PF2=b2tan∠F1PF22=b2tan θ.

由35=cos∠F1PF2=cos 2θ=cos 2θ－sin 2θcos 2θ+sin 2θ=1－tan 2θ1+tan 2θ，解得tan θ=12.所以S△F1PF2=6×12=3.

又S△F1PF2=12|F1F2||yP|=12×23×|yP|=3|yP|，所以3|yP|=3，解得y2P=3.

所以x2P=9×1－36=92.

因此|PO|=x2P+y2P=302.

4 问题溯源

溯源1“爪型”三角形与斯特瓦尔特定理

在三角形中，连接一个顶点与其对边上任意一点，因其形状类似爪子所以被称为“爪型”三角形，如图3所示.“爪型”三角形的问题可以利用cos∠APB+cos∠APC=0和余弦定理求解.

1746年，蘇格兰数学家斯特瓦尔特发现了这种关系，并由此给出了“爪型”三角形中五边的关系：AP2=BPBC·AC2+CPBC·AB2－BP·CP.当然，究其本质，是余弦定理的运用.

当点P特殊时，还可以得到如下推论：

若AP为中线，则AP2=12AB2+12AC2－14BC2.

若AP为角平分线时，则AP2=AB·AC－BP·CP.

溯源2隐圆问题

如图4，设线段AB的长度为定值，∠ACB=θ为定值，则点C的轨迹是以O1，O2为圆心，以AB2sin θ为半径的两段圆弧.圆心O1，O2在线段AB的中垂线上，距离为AB2|cot θ|.

实际上，文中给出的8种解题思路是从不同角度对斯特瓦尔特定理和隐圆问题的证明和应用.

5 问题拓展

在“爪型”三角形中，P可以是BC上的任意一点.

（2022年全国高考数学甲卷理科第16题）已知△ABC中，点D在边BC上，∠ADB=120°，AD=2，CD=2BD，当ACAB取得最小值时，BD=.

解：略.

“爪型”三角形是解三角形问题中最常见的一种类型，解决

此类问题的常规思路就是利用余弦定理或向量求解.

6 反思建议

2023年全国高考数学甲卷理科第12题中涉及的方法很典型，解三角形问题常规入手方式就是正弦定理与余弦定理，因为题目是求三角形的中线，所以又可以联想中线公式、中线的向量表达式、极化恒等式等.同时，该题套有椭圆外衣，因此还可以从椭圆的参数方程、椭圆焦点三角形面积的二级结论入手.

备考时，提醒学生注意数形结合，注重三角形边角关系的转换，以及与其他知识的联系.鼓励学生一题多解、多题一解，并让学生自己归纳总结此类题型的解题技巧和思想方法，培养学生的数学运算、逻辑推理等数学核心素养.