基于队长策略捕鱼算法的改进及性能测试

梁 晓 龙

(石家庄职业技术学院 食品与药品工程系,河北 石家庄 050800)

0 引言

捕鱼算法(an optimization algorithm on using fishing strategy,简写为“FSOA”)是模拟渔夫捕鱼行为策略而提出的一种群智能优化算法[1-2].该算法因具有鲁棒性强、收敛速度快、搜索策略简单、容易编程实现等优点,已被广泛应用于水资源预测[3]、车间调度[4]、大数据中用户特征信息优化定位[5]、无线电频谱分配[6]等诸多领域,并取得了较好的效果.捕鱼算法因其良好的寻优性能而被不断改进和研究,有自适应精英捕鱼算法[7]、与蜜蜂进化型遗传算法相结合的算法[8]、改进二进制捕鱼算法等[9].智能优化算法是通过模拟自然界生物行为或者自然现象规律而提出的搜索策略,如遗传算法、粒子群算法、蚁群算法、灰狼算法、鲸鱼算法、蝙蝠算法、布谷鸟算法等[10-13].诸多学者对智能优化算法的寻优性能、搜索策略、算法复合策略、推广应用展开了研究,极大地丰富了优化技术理论,推动了智能优化算法的发展.传统的优化方法(线性规划法、最速下降法、二分法等)仅适合解决简单问题,遇到多维度、非连续、多极值的问题时,则存在收敛速度慢、计算量随维度增加呈指数增长、容易陷入局部极值等问题.智能优化算法在解决复杂问题、寻找较优方案时具有明显的优势.

本文针对捕鱼算法缺少信息共享机制、对当前群体最优信息利用不充分的问题,提出队长策略捕鱼算法(fishing algorithm based on captain strategy,简写为“C-FSOA”),以期提升捕鱼算法的寻优性能.

1 基于队长策略捕鱼算法的改进

1.1 捕鱼算法的假设和方式

捕鱼算法模拟渔夫捕鱼行为策略基于以下假设:(1)搜索空间的静态性和初始未知性.搜索空间的静态性是指搜索空间内任意点的适应度值不随搜索的进行而改变;初始未知性是指在搜索开始前,对搜索空间内任意点的适应度值均是未知的.(2)渔夫的趋优性、贪婪性和排斥性.趋优性是指渔夫总是趋向于在鱼群密度大的区域内搜索;贪婪性是指对于鱼群密度较大的区域,渔夫会用网眼更小的渔网捕鱼以期捕获更多的鱼;排斥性是指渔夫之间相互排斥,避免在相同区域内搜索.

捕鱼算法中各渔夫根据自己的状态分别按照移动搜索、收缩搜索和随机搜索3种策略独立搜索,能够较好地避免陷入局部极值,并最终搜索到最优解.

1.2 队长策略

各渔夫按照移动搜索、收缩搜索和随机搜索各自独立搜索,不能充分发挥群体行为中最优个体的指导作用.针对这一现象,提出队长策略,即所有渔夫完成一代搜索后,渔夫群体共享搜索信息,找出当前最优个体确定为队长,在之后的搜索进程中处于劣势的渔夫群体(寻优适应度值排名靠后的渔夫群体)认为队长周围的鱼群密度会更高,在搜索过程中选择跟随队长进行搜索的策略.因渔夫之间的排斥性,仍然保留处于优势的渔夫群体(寻优适应度值排名靠前的渔夫群体)独立搜索,从而避免过早陷入局部极值.

1.3 实现步骤

步骤一,初始化.N个渔夫随机选择自己在搜索空间D内的初始位置

步骤二,独立搜索.各渔夫i在当前位置xi为中心的邻域内,随机选取p个搜索点,见公式(1),并求其适应度值).

其中,N为群体规模;rk∈(0,N]为渔夫搜索半径调控系数;T为设定的迭代阈值;t为渔夫搜索迭代次数；为t代渔夫i的搜索中心;为t代渔夫i的第k次搜索;rand(0,1)为随机数,模拟渔夫撒网的不确定性;A∈[1,10]为收缩调控系数;p为渔夫在当前位置的搜索次数.

步骤三,移动搜索.渔夫i当前搜索的最大适应度值|i=1,2,…,N;k=1,2,…p},判断其是否大于原中心位置xi的适应度值,若f()＞f(),则渔夫i的中心位置移动至;反之,渔夫i中心位置不变,继续搜索.

跳出机制:若搜索到的最优解满足设定的误差要求或迭代次数达到迭代阈值T,跳出搜索,输出最优解,否则搜索继续.

步骤四,信息共享.当渔夫独立搜索进行到T1代后,共享所有渔夫的当前适应度值,并对渔夫群体按其适应度值排序.取适应度值最大的渔夫为队长,适应度值较小的[τ(N-1)]个(τ为追随控制系数,控制追随队长移动的渔夫数量)渔夫向队长所在位置移动,并进行搜索,迁移方式见公式(2).剩余适应度值较大的N-[τ(N-1)]个渔夫继续保持独立搜索.

其中,为队长的当前中心位置；为渔夫i当前中心到队长所处中心的向量;κ∈(0,1)为迁移控制系数,越靠近1,表示渔夫个体对于队长的迁移程度越高.

步骤五,迁移.渔夫在向队长移动之后在新的位置独立搜索,转入步骤二.

2 C-FSOA搜索性能测试

2.1 函数测试

为测试C FSOA 寻优性能,选取能够反映寻优速率、全局收敛性能的6 个典型函数进行测试[11],并与FSOA 的寻优性能进行比较.6 个测试函数表达式、约束区间及理论最优解见表1.其中,DeJong F1 函数为单峰函数;Camel 函数、Schaffer F6函数、Shubert函数为多峰函数,存在较多的局部极值,容易使优化算法陷入局部极值,影响其寻优速率效果,这些函数能够较好地反映出被测试算法的全局收敛性能;Rosenbrock函数为典型的单峰病态函数,其理论全局最优解位于函数的一个狭窄凹区间内,寻找难度较大,运用此函数能够较好地反映出被测试算法的优化效率.

作为对比测试,FSOA 算法和C-FSOA 算法在测试过程中群体规模N、迭代阈值T、初始化状态等参数设置均相同,见表2.

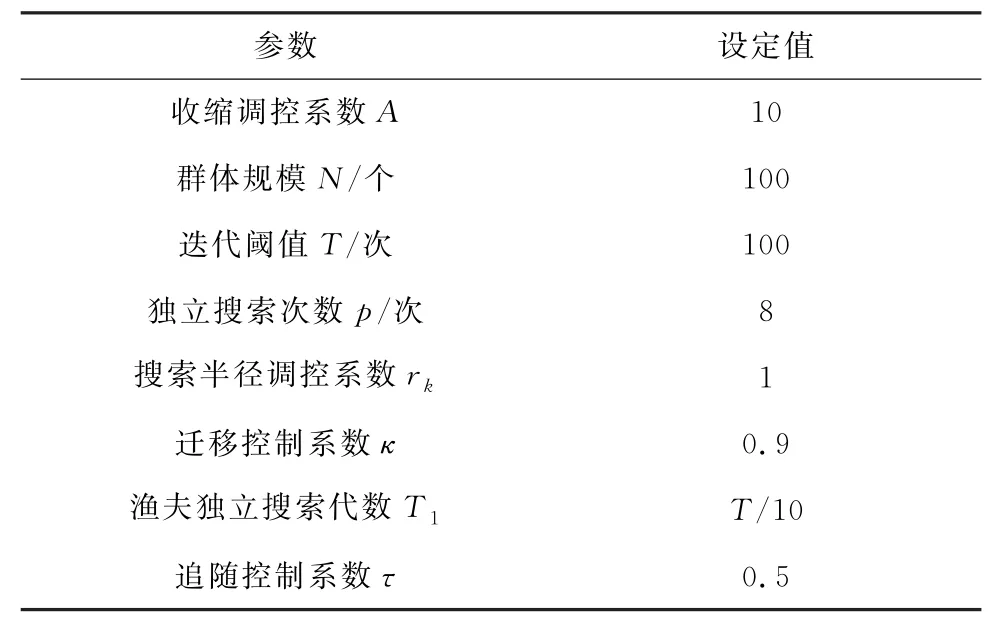
表2 FSOA 与C-FSOA 参数设置

2.2 FSOA 和C-FSOA 测试结果分析

2.2.1 寻优速率

在参数设定相同的条件下,FSOA 和C-FSOA分别对6个测试函数迭代10次.为方便表示,各测试函数的适应度值设置为:G1=1/(2+f1),G1=1/(1+f2),G3=1/(1+f3),G4=1/(188+f4),G5=1/(1+f5),G6=1/(1+f6).两种算法对6个测试函数的适应度值随迭代次数t变化趋势见图1.

图1 FSOA 和C FSOA 对6个测试函数适应度值G j 的迭代曲线

由图1可以看出,测试函数f1,f2,f3,f5,f6的C-FSOA 寻优速率具有明显优势;因多峰测试函数f4存在较多的局部极值,FSOA 寻优速率更快一些.整体测试反映出C-FSOA 在信息最优个体“队长”指导下寻优速率有明显的提升.

2.2.2 寻优性能

为进一步验证算法的寻优性能,在参数设定相同条件下,FSOA 和C-FSOA 分别对6个测试函数独立求解100次.分别记录100次寻优结果的最优解、平均值、标准差和最差解,以此分析两种优化算法的寻优性能.数据见表3.

表3 FSOA 与C-FSOA 测试结果比较

由表3 可以看出,对于Rosenbrock 函数、De-Jong F1函数、Rosenbrock 2函数,C-FSOA 优化结果的最优解、平均值、标准差和最差解较与FSOA优化的结果均提高了几个数量级;对于Camel函数,两种算法均找出了最优解,但是C FSOA 的寻优结果标准差要比FSOA 的寻优结果标准差小两个数量级,表明C-FSOA 寻优稳定性更好;对测试函数Schaffer F6函数的寻优效果,两种算法的测试结果相当,均能找到理论最优解;对于Shubert函数,C-FSOA 寻优结果中最差解、平均值和标准差均劣于FSOA 寻优结果,但也搜索出了理论最优解,寻优性能也属合格.综合来看,C-FSOA 在寻优速率、稳定性方面均有明显提升.

3 结论

在参数设置相同的情况下,C-FSOA 算法的稳定性和收敛效率相较于FSOA均有所提高;而针对局部极值较多的函数寻优性能有所降低,其原因是部分渔夫在追随队长捕鱼之后会影响渔夫的多样性,对多极值函数的搜索效率会相应的降低,但是也搜索到了最优解,对该函数的搜索也是合格的.测试结果表明,基于队长策略的捕鱼算法利用群体最优个体信息能够在一定程度上提升算法的搜索效率,原理简单,容易编程实现,具有一定的推广应用价值.