基于改进SGM算法的双目立体匹配*

宋 坤,易怀安,舒爱华,宋欣茹,黄杰锋

(1.桂林理工大学机械与控制工程学院,桂林 541006;阜阳师范大学计算机与信息工程,阜阳 236000)

0 引言

双目立体视觉技术是计算机视觉中的一个重要领域,其原理是利用双目相机模仿人的双眼获取一对二维图像,通过立体匹配算法从一对二维图像中计算出三维结构信息。该技术具备操作简单、效率高、成本低的优点,因此有广泛的应用领域,如计算机视觉[1-2]、机器人工业[3]、自动驾驶技术[4-5]、遥感测绘[6-7]等方面。双目立体视觉技术的主要工作流程包括5个步骤:图像采集、相机标定[8]、立体校正、立体匹配和三维重建[9]。其中,最核心的步骤为立体匹配。它是根据左右相机获取的一对图像,建立被拍摄物体在左右图像之间投影点的对应关系,通过立体几何原理计算投影点的视差,从而得到视差图。根据视差图可以恢复其深度信息,重构物体的三维空间几何。因此,立体匹配获得视差图的精度直接决定三维重建得到立体场景的精确度,所以,提高立体匹配的精度成为了当前研究的热点。

为了提高立体匹配的精度,科研人员进行了一系列的研究。根据优化理论方法的不同可分为全局立体匹配、局部立体匹配和半全局立体匹配。全局立体匹配算法使用全局优化算法进行视差估计,主要有DP[10]、GC[11]、BP[12]算法。该类算法是在能量函数框架下,把立体匹配问题转换为求解能量函数最小化问题。该算法虽然有较高的精度,但是该算法复杂程度较高,耗时长,难以达到实时性。而局部立体匹配使用的是局部优化,主要是利用SSD、SAD、Census等局部代价函数进行视差估计[13],该类算法灵活多变且运算速度快,但是精度较低。因此,HEIKO[14]提出一种半全局立体匹配(SGM)的方法,该算法通过沿图像上的多条(通常为4或8条)独立路径求解一维最小化问题来近似全局解。虽然较好地中和局部匹配和全局匹配的优缺点,但在处理遮挡区域以及视差不连续区域的能力较弱,在遮挡区域的地方出现较大的偏差。近几年由于深度学习的快速发展,CAO、CHEN等[15-17]提出了AMDCNet、PGNet、PSNet等立体匹配方法,虽然该方法能很好的解决以上问题,且匹配精度也很高,但是该类方法泛化能力不足,需要依赖大量的训练数据集,立体匹配数据集采集难度大,成本高,且应用的场景也过于局限。因此该类方法不能很好的应用到实际场景。

本文针对SGM算法在图像匹配中遮挡区域以及视差不连续区域的能力较弱问题,在SGM算法基础上进行视差优化,提出一种基于SGM算法结合泛洪填充算法[18-20]和中值平滑的视差优化方法。泛洪填充算法是模拟流体扩散过程用特定的颜色填充联通区域的一种算法,该算法被广泛应用在二维空间中确定连通区域的图像处理中,且该算法填充不仅效率高且有较高的准确性,因此利用该算法对视差图中的遮挡区域以及视差不连续区域进行空洞填充,接着对视差图进行中值平滑处理,进一步对视差进行细化的方案,大大增加了视差图的匹配准确度和适用性。

1 算法原理

本文算法流程如图1所示,输入左右相机采集的图像对,经过Sobel算子处理、代价计算、代价聚合、视差计算、唯一性检测、泛洪填充算法、中值平滑及左右一致性检测等步骤最终生成视差图。首先,本文在代价计算过程中使用BT代价计算,相较于传统的互信息像素代价计算降低运行时间的同时也提高匹配的精度。然后通过对多路径的一维约束进行求解各路径的能量函数计算像素点总的匹配代价。采用WTA算法进行视差计算。本文在视差优化阶段使用唯一性检测、亚像素插值对错误的视差进行剔除,接着通过泛洪填充算法对视差弱纹理、重复纹理以及视差不连续区域进行填充,利用中值平滑在剔除噪点的同时保留物体的边缘特征,最后生成视差图。

1.1 SGM算法

1.1.1 预处理

本文在采用Sobel算子对初始图像进行水平处理,该算子根据相邻点灰度的加权差,在边缘处达到极值这一现象检测边缘。对噪声具有平滑作用,可以精准的计算出边缘信息,因此使用SobelX水平算子对输入图像的边缘进行提取,水平方向进行梯度滤波处理。

然后再经过一个函数将SobelX处理后图像上像素点的像素值P,映射到一个新的图像,像素值为Pnew,映射函数为:

(1)

式中:preFilterCap是一个参数,可以根据不同的需求进行调整,经过上述处理,可以得到图像的梯度信息,用于下一步的代价计算。

1.1.2 匹配代价计算

(2)

(3)

取两个代价的最小值:

C(xR,y,d)=min(cos1,cos2)

(4)

1.1.3 代价聚合

通过图像上多个方向上的一维路径约束,建立一个类似全局的马尔科夫能量方程,代替全局匹配中的能量函数,每个像素最终的匹配代价是所有路径的叠加,每个方向方向都按照动态规划的方法进行能量积累,如式(5)所示。

(5)

式中:C(P,d)代表的是基于BT代价计算的初始代价项,P是像素点(xR,y),r代表聚合路径,P1,P2是惩罚因子,数学模型如式(6)所示。

P=x*number*SAD*SAD

(6)

式中:x为常数,number为待匹配图像通道数,SAD是代价计算的窗口大小。

将每个方向的匹配代价进行累加得到该像素点总的匹配代价,公式为:

S(P,d)=∑rLr(P,d)

(7)

1.1.4 视差计算

在本文算法中,采用赢家通吃(WTA)算法进行视差计算,即每个像素都选择最小的代价聚合值所对应的视差作为初始视差(D(p)),一般会把每个像素计算到的视差以左图为参考存储视差值,再结合图像的内外参数即可转换为深度图,计算公式为:

(8)

1.1.5 后处理

SGM算法中后处理阶段主要包括:唯一性检验、亚像素插值、左右一致性检测。本文在后处理阶段做了大量的处理,在经过左右一致性检验后,视差图会有大量的无效区域,对此本文加入泛洪填充算法与中值平滑,对泛弱纹理、重复纹理以及视差不连续区域进行填充,再用中值平滑对图像的噪点进行剔除。

左右一致性检查即把左右图像的位置进行对调,对右图像进行视差图计算,并对照两个视差图的同名点对是否能够相互匹配,一般是把左视差图的每一个像素点计算出同名点在右视差图中的像素点的位置。再判断视差值之差的绝对值是否小于一个阈值,如果超过阈值则视为不一致,即该位置视差为无效值。计算公式为:

(9)

1.2 泛洪填充算法

泛洪填充算法[15-16]是模拟流体扩散过程用特定的颜色填充联通区域的一种算法,该算法被广泛应用在二维空间中确定连通区域的图像处理中。从一个选定的像素点F(x,y)出发,根据该像素点与周围像素点灰度值的差值对周围目标像素点判断是否属于该联通区域,满足判断则对该点进行填充,并将该目标点作为新的种子点进行下一轮填充过程,直到完全填充该联通区域。泛洪填充最常见的有四连通和八连通两种填充算法,如图2所示。

(a) 四连通填充方向 (b) 四连通填充区域

由图2可以看出,四连通填充算法是指从选定的像素点F(x,y)出发,对上、下、左、右4个填充方向上的相邻像素点进行判断,以确定是否对该填充方向进行扩展,见图2a。八连通填充算法则是在四联通填充的基础上加入了左上、左下、右上、右下4个填充方向,见图2b;图2c和图2d分别为四连通和八连通填充区域。相比较两种算法,后者会出现跨区域填充的情况,对于细节较多的视差图来说会增大视差图的误差,而且计算量较大、耗时较长。而四联通不仅会减少计算量在对视差图空洞填充中的“鲁棒性”较强,因此本文选用四联通填充算法对视差图中的空洞进行填充,在视差图中图像中,由于无效点(其灰度值为0)与有效点之间的灰度值是存在突变,可以利用泛洪填充算法找到空洞中的某一非零灰度像素点作为起始像素点,对该联通区域进行填充以获取匹配度更高的视差图。

1.3 中值平滑

中值平滑是一种基于排序统计理论的图像处理技术,同时也是一种邻域运算,是生成一个滤波模板,通过从视差图中的二维模板取出奇数个像素点的灰度值进行排序,用排序后的中值取代该滑动窗口中心像素的灰度值,从而达到对视差图的平滑处理。假设w为输入的二维模板,能够在整幅图像上滑动,通常尺寸为3*3或5*5区域,也可以是不同的形状如线状、圆形、十字形、圆环形等。一般设{xij(i,j)∈I2}表示视差图各点的灰度值。窗口大小为A,yij是窗口A在xij像素点的中值,则有:

yij=Med{xij}=Med{xi+r,(i,s),(r,s)∈A,(i,j)∈I2}

(10)

中值平滑是一种经典的平滑处理方式,它的目的是保护视差图边缘特征的同时可以填补视差图中噪声点,能够克服线性滤波器带来的视差图像中细节模糊等弊端。

2 评价指标

为了验证算法参数的有效性,我们引入均方根误差(RMSE)、峰值信噪比(PSNR)对视差图进行分析[18],同时为了更详细地量化匹配结果,引入平均结构相似性(MSSIM)评价指标计算本文算法得到的视差图与真实视差图像相似性。

2.1 均方根误差

均方根误差反映的是变量间的差异程度,是一种基于像素误差的图像质量客观评价指标,用于衡量生成视差图像和真实视差图像之间的差异,MSE越小,表示生成的视差图像效果越好。表达式如下:

(11)

2.2 峰值信噪比

峰值信噪比,用于衡量图像有效信息与噪声之间的比率,是衡量图像失真或噪声水平的客观指标,能够反映图像是否失真。PSNR的值越大,表示图像的匹配质量越好。公式为:

(12)

式中:M*N表示图像的大小,X(i,j)和Y(i,j)表示两幅图像的灰度值。

2.3 结构相似性

结构相似性是一种用以衡量两张图像相似程度的指标,它分别从亮度、对比度、结构3个方面度量图像相似性,尤其反映了图像的轮廓,细节等的相似度,很适合在本实验中用来衡量生成视差图与真实视差图之间的相似程度的客观评价指标,MSSIM值越大,说明与真实视差图像更接近,视差图效果越好,计算公式为:

MSSIM(X,Y)=

(13)

式中:μXk、μYk分别表示图像X和Y的均值,σXk、σYk分别表示图像X和Y的方差,σXkYk表示图像X和Y的协方差,C1、C2、C3为常数,为了避免分母为零的情况。

2.4 实验参数选取

在SGM算法的参数中,有3个关键参数对视差生成效果有很大影响,即SADNowSize、NumDisparities和UniquenessRatio。

(1)SADNowSize(SWS):计算成本步骤中SAD窗口的大小SW应该是奇数,一般在范围(3,11)内。

(2)NumDisparities(NDis):视差窗口,即最大和最小视差值之间的差值,必须是16的整数倍。

(3)UniquenessRatio(UniR):主要是为了防止不匹配,这个参数对最终的匹配结果有很大的影响。在立体匹配中,如果存在不匹配,遇到障碍物检测应用程序将非常麻烦。此参数不能为负,可在范围(5,15)内获得。

因此,我们将重点分析SWS、NDis和UniR的参数,以选择最佳算法参数。利用MSSIM与RMSE对视差图进行了评估。首先,在程序中,我们设置参数的初始值,然后调整其中一个参数(保持其他参数不变),使值变化最大。同样,我们调整其他参数以使其达到最佳状态,最后选择所有最佳参数。设置参数的初始值:SWS=5、NDis=64和UniR=10。我们仅以teddy的视差图为例,图3是配重参数SWS=5和UniR=10时。更改NDis值时Teddy视差图所对应的MSSIM与RMSE的评价指标,NDis的值范围为:(16～112)。

图3 相对于Ndis的teddy变化(SWS=5,UniR=10)

从图3可以看出,当Ndis=16、32、48时,teddy的视差图中的RMSE值在不断的下降,MSSIM值在不断的提高,视差图在随着Ndis值的增大精度在不断地提高,当Ndis=80、96、112时,teddy的视差图中的RMSE值在不断的上升,MSSIM值在不断的下降,视差图在随着Ndis值的增大精度在降低,由此看见,当Ndis=64时,teddy的图像匹配效果与真实视差最接近,此时的匹配效果最好。

图4是配重参数Ndis=64和UniR=10时。更改SWS值时Teddy视差图所对应的MSSIM与RMSE的评价指标。

从图4可以看出。当SWS=3、5、7、9、11时,teddy的视差图中的RMSE值在不断的上升,MSSIM值在不断的下降,由此可见当SWS增大时视差误差越大,但是视差图的相似性越大。为平衡二者的优劣,本文取SWS=5。

图5是配重参数Ndis=64和SWS=5时。更改UniR值时Teddy视差图所对应的MSSIM与RMSE的评价指标。

从图5可以看出,当参数UniR改变时,teddy的图像匹配效果没有显著变化。为了评估生成的teddy视差图像的全局精度,平衡二者的优劣,本文取UniR=12。结果表明,组合(Ndis=64,SWS=5,UniR=12)产生的结果最准确。

3 实验结果及分析

为了验证本文提出的视差图像优化算法的性能,进行3组实验。分别选用teddy、Books、Dolls、Cloth进行实验验证,该实验的目的是通过评价指标定量评估算法性能;本文算法的代码通过PyCharm Community Edition 2021.3.2中OpenCV库实现,在配备Intel(R) Core(TM) i5-10400F 2.90 GHz的CPU以16GB内存的计算机上运行。

3.1 实验结果

在Middlebury立体匹配数据集中选取teddy、Books、Dolls、Cloth场景,参考以上实验中的主要参数取值,用原始SGM算法与本文改进SGM算法分别进行实验,得到结果如图6所示。

图6 teddy、Books、Dolls、Cloth的立体匹配结果

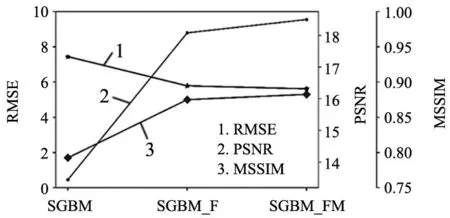
图7 改进前后RMSE、PSNR、MSSIM指标平均值变化曲线

通过与传统SGM算法所生成的视差图比较,本文所提的泛洪算法对视差图的遮挡区域有很好的填充效果,如图6c所示。中值平滑可以剔除对视差图中的噪点,从而进一步改善视差图,如图6d所示。

3.2 结果分析

为了进一步验证本文改进的SGM算法的优越性,利用均方根误差(RMSE)、峰值信噪比(PSNR)、结构相似性(MSSIM)评价方法对实验结果进行量化评价。从而对本文所改进的SGM算法进行量化分析。定量评价结果如表1所示,其中b列是传统SGM算法得到视差图的量化评价,c列为在SGM算法的基础上引入泛洪填充算法所得到视差图的量化评价,d列为在c列的基础上再对视差图进行中值平滑处理所得到视差图的量化评价。

表1 基于Middlebury数据集部分图像匹配量化指标

通过对表1中的量化指标分析可以看出,所提改进SGM算法增加了泛洪填充算法与中值平滑算法的方法,仅在SGM算法中加入泛洪填充算法,RMSE指标平均值下降1.66,PSNR指标平均值上升4.64;MSSIM指标平均值上升8.25%,由于改进后的视差图是根据空洞边缘的视差值来决定空洞的视差值填充,对于丢失的部分可以得到有效的补充,使得改进后的算法所生成的视差图准确度得到提升。在后处理阶段加入中值平滑后,RMSE指标平均值下降0.17;PSNR指标平均值上升0.42;MSSIM指标平均值上升0.75%,中值平滑可以很好的去除视差中的噪点,从而提高视差的精确度。通过对3项指标的量化分析可以看出,改进后的SGM算法,RMSE指标平均值下降1.83;PSNR指标平均值上升5.06;MSSIM指标平均值上升9.00%。与传统SGM算法相比较之下,本文改进的SGM算法在立体匹配中性能有较高的提升。

4 结论

本文提出一种在SGM算法基础上引入泛洪填充算法以及中值平滑。在视差后处理阶段采用泛洪填充算法对图像匹配中遮挡区域以及视差不连续区域中空洞进行填充,先是对空洞边缘的信息进行选取,然后基于空洞的边缘信息进行空洞填充,不仅很好的保留图像的边缘信息,而且对视差图的空洞很好的进行填充,接着再对图像进行中值平滑处理,对视差图中的噪点进行剔除。与传统SGM算法相比本文所改进的立体匹配准确度提高了9.00%。