考虑能耗的多AGV系统无冲突路径规划*
2024-01-03陈晶晶方叶祥王文凤
陈晶晶,方叶祥,王文凤
(南京工业大学经济与管理学院,南京 211816)
0 引言
自动引导车在货物运输时能够有效的提高搬运效率、降低生产成本,是具有敏捷性、自动化等优点的运输工具[1],现如今节能减排已成为全球制造业实现可持续发展的共识[2]。制造型企业车间开始推行自动化改进,引入AGV进行货物运输,因此为AGV规划出一条无冲突且节能的路径,既可以提高AGV系统的整体运行效率也可以达到节能减排的效果。
AGV的路径优化已经成为国内外于仓储车间中的主要研究问题之一[3],为了规划出无冲突的路径。杨洁等[4]对仓储分拣库区进行数学建模,采用两个冲突解决方式不同的模型为分拣库区多AGV规划出无碰撞路径。于会群等[5]以AGV完成任务的空载时间与AGV的空置率为优化目标,改进Q-Learning算法生成多AGV无冲突路径,最终完成多AGV路径优化。王然等[6]通过构建奖惩矩阵的形式,提出一种在线学习的Q-Learning算法,实现多AGV的无冲突路径规划。泰应鹏等[7]提出以时间窗为基础的多AGV路径规划方法,对路径冲突进行侦测,通过路径变换、策略等待等方式解决。刘维民[8]为解决多AGV运行路径利用率不均衡造成的碰撞问题,而提出基于时间窗的路径算法,最后为多AGV系统规划处一条利用率均衡且无冲突的路径;张中伟等[9]通过时间窗检测冲突类型,对多AGV系统规划出无冲突路径,将等待时间、行驶距离、任务紧急程度等作为量化动态优先级策略。
针对车间AGV节能减排问题,郭亚铭等[10]以最短运输距离和最小化能耗为目标优化制造车间单AGV节能路径规划;李俊兰等[11]针对AGV多任务运输以运输距离和能耗作为优化目标,对AGV多运输任务时合理安排顺序和规划运输路径能够提升AGV能效;吴立辉等[12]建立节能路径模型,优化目标为最小能耗和搬运距离,提出改进Dijkstra算法和NSGA-Ⅱ算法集成的多载具AGV节能路径规划。WANG等[13]在研究AGV调度问题时,根据车间实际复杂度考虑对AGV能耗的影响,合理安排AGV的运输路径;宋栓军等[14]在时间窗的基础上,建立受负载和时间控制的能耗计算方法,以系统能耗最低为目标构建AGV冲突消解模型,该方法可以减少系统内的AGV的充电次数,提高多AGV系统的工作效率。
上述文献主要研究了多AGV无冲突路径规划及考虑单AGV能源消耗的路径规划,然而现阶段针对多AGV系统规划无冲突路径时考虑能耗指标、实现绿色节能路径的较少,并在仓储车间多AGV进行物流运输领域开展节能减排路径规划的研究总体而言仍较为匮乏。针对现有多AGV能耗优化无冲突路径存在的问题,本文以仓储车间环境下多AGV为研究对象,提出两阶段优化方法。第一阶段建立多目标节能优化第模型,利用算例分析验证模型的可靠性;第二阶段对初始路径进行冲突检测及解决。最后以案例研究验证了模型的有效性。
1 问题描述和建模
1.1 问题描述
本文采用拓扑图表达仓储车间环境,而仓储车间内路线并不是完全相通的,会有部分区域禁止通行。引入三维变量定义部分连通无向图为G=(W,A,B),其中W={0,1,2,…,n+1}为货架和路径交叉等具有特殊意义的节点集合,A={(i,j):i,j∈W,i≠j}是车间过道边的集合,用dij表示边之间的距离。B=min(i,j)表示寻找两个节点间的最短距离。K={1,2,…,k}为AGV数量集合,每台AGV起始点在同一位置,且各自有不同的目标节点。多AGV执行任务时互为彼此的动态障碍物并且会产生能耗,问如何规划出全局无冲突多AGV系统搬运路径,以使得总时间最短,并且AGV总能耗最小,建模过程服从如下假设。
(1)本文针对单行双向潜伏式AGV;
(2)AGV以匀速直线和匀速转弯两种速度行驶;
(3)每台AGV的运输的载重量、体积不会超过其额定载荷;
(4)AGV装卸物料的时间包含在搬运时间以内;
(5)AGV不考虑AGV任务途中充电情况,且能连续工作无障碍。
1.2 模型建立
建立模型,定义参数和决策变量如表1所示。

表1 模型参数和决策变量定义表
(1)搬运时间。分析AGV搬运时间,首先要确定AGV的行走距离D。AGV行走距离D主要包括运输遍历节点间的距离D1和节点区域行驶距离Dnode,其中:
(1)
(2)
式中:nL表示直行通过节点数目,nT表示转弯通过节点数目,即:
D=D1+Dnode
(3)
小车在运输过程中速度保持不变,AGV匀速直线行驶的总距离Dulm和匀速转弯行驶的总距离Dutm分别为:
Dulm=D1+2RnL
(4)
(5)
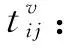
(6)
则AGV完成所有搬运任务的总搬运时间表示为:
(7)
(2)能耗。为降低分析AGV能耗难度,本文主要从AGV的运动角度进行切入,将搬运过程总能耗分解为待机能耗、匀速直线运动能耗Eulm和匀速转弯运动耗能Eutm。Pso为AGV的待机运动功率,故AGV系统搬运过程最小总能耗表示为:
(8)
AGV做匀速直线运动时加速度为零,匀速转弯时,车辆与地面的静摩擦力完全提供向心力。设AGV匀速运动共有u个阶段,其中匀速转弯通过的节点有nT个,故匀速直线阶段有u-nT个。因此,第y个匀速运动的驱动力。
(9)
式中:my表示第y个匀速运动阶段AGV和货物的总质量,kg;Cr为滚动摩擦系数。
即可计算出AGV匀速转弯的总耗能Eutm:
(10)
式中:η表示行走驱动电机功率因数,θ表示AGV的转向角度,R1、R2、R3、R4表示AGV四个车轮的转弯半径。
进而可计算出AGV匀速运动在直线路段的总能耗Eulm:
(11)
现以最小搬运时间和能耗为优化目标,可建立数学模型:
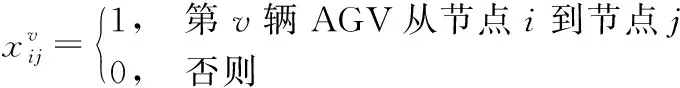
(12)
(13)
(14)
(15)
(16)
m0≤my≤m0+Q
(17)
约束式(12)~式(13)表示变量的定义;约束式(14)~式(15)表示每个节点都能被访问一下;约束式(16)表示每个任务节点只能由一辆AGV运输;约束式(17)表示AGV运输重量不能超过其最大载重。
2 问题求解
本文多AGV节能无冲突路径规划问题,提出两阶段优化方法,如图1所示。第一阶段建立多目标数学模型,根据NSGA-Ⅱ算法求解出初始节能路径;第二阶段对路径冲突进行检测与解决,得出最优路径。

图1 求解框架
2.1 NSGA-Ⅱ算法
在选择、交叉、变异等算法上采用传统NSGA-Ⅱ算法[16],鉴于本问题设计路径和能耗两类,本文重点介绍编码和解码算法,其余不作赘述。
2.1.1 编码
针对n个搬运任务的场景,路径规划核心是对n个搬运任务搬运能耗最少的最短搬运路径的选择。采用实数编码方式,将n个搬运任务随机排列在染色体上,染色体上基因总数与搬运任务相对应,且每一个基因在染色体上只表达一次。例如:3辆AGV,10个搬运任务的实数编码如图2所示。

图2 编码示例
则3辆车的搬运任务分别表示为:0-2-5-8-0,0-4-7-10-1-0,0-3-7-9-0。
2.1.2 解码
步骤1:根据染色体编码获得搬运任务基因位信息,按照满足搬运重量条件约束下,分配到各辆AGV;
步骤2:若v辆AGV搬运重量小于等于极限重量,则染色体内第i个搬运任务分配到该AGV;若v辆AGV搬运重量大于极限重量,则染色体内第i个搬运任务分配到第v+1辆AGV;
步骤3:获得各AGV的搬运路径及路段间的距离,分析AGV行驶过程中的运输载重量及拐弯次数,计算直线和拐弯行驶的能耗,通过式(8)求得能耗值、式(7)求得时间;
步骤4:重复步骤1~步骤3,直至解码完成。
2.2 模型可靠性分析
为验证1.2节中提出的多目标模型的可靠性,以文献[15]中的算例为例。应用本文模型,采取NSGA-Ⅱ算法求解得出初始节能路径,本文计算结果与文献[15]计算结果对比如表2所示。

表2 结果对比
由表2可知,本文模型的计算结果与文献[15]的结果一致度较高,因此验证了本文提出多目标节能模型的可靠性。
2.3 AGV冲突检测及避撞算法
依据NSGA-Ⅱ算法求解出的初始节能路径,判断多AGV系统同时运行时可能发生的冲突[17],常见冲突类型:相向冲突、节点冲突和占位冲突。本文主要采用时间窗[9]的思想进行判断AGV冲突类型并通过避撞机制解决冲突。
2.3.1 主动避撞机制
(1)时间窗右移方法。时间窗右移是处理冲突常见的策略,当某个路段出现AGV冲突,采用时间窗右移时,所有受影响的路段时间窗都需要推迟一段时间,流程如图3所示。
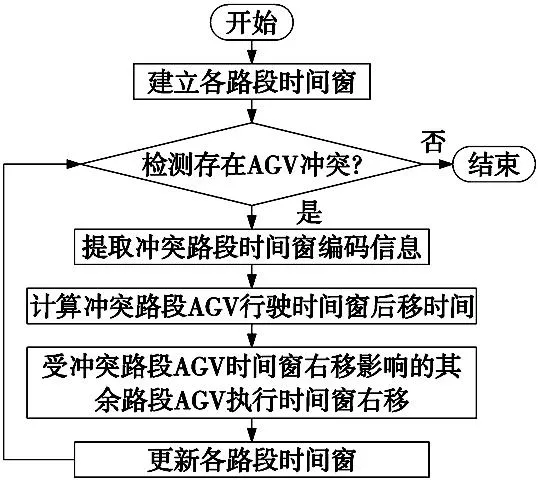
图3 时间窗右移流程

图4 基于时间窗的动态优先级的任务分配算法
(2)动态优先级策略。动态优先级策略考虑的因素有等待时间、距离以及负载程度,主要原因如下:①当AGV发生冲突时,若等待时间过长,设置高优先级可以减少过长的等待时间,同时可以避免因长时间等待而引发新的占位冲突;②考虑AGV路径距离,当AGV到任务节点的剩余路径较长时,设置高优先级优先执行任务,可有效减少等待浪费的时间,从而缩短运输时间;③实时考虑AGV行驶时的载重情况,当AGV到目标点的负载较大,需提高AGV优级才能使其尽早完成运输任务。优先级数学模型:
(18)

2.3.2 被动避撞机制
多AGV系统的实际运行中,会出现一些不可预见的因素影响车辆的运行,例如:AGV突发故障、货物掉落等。当遇这些情况时,采取被动避撞机制对AGV进行路径二次规划。具体步骤如下:
步骤1:根据AGV上传的位置路段设为不可通行区域,同时为后续要经过此路段的车辆重新规划路线,得出新的初始路径;
步骤2:根据求解出的初始路径,建立各路段时间窗,再次采取时间窗与动态优先级结合的主动避撞机制检测冲突并调整至全局无冲突路径。
3 案例研究
3.1 案例描述
为验证本文提出优化方法的有效性,本文采用某太阳能光伏组件制造企业的一个硅片仓储车间数据进行实验。所建立车间拓扑地图如图5所示(0为拣货区,01,02为AGV停靠点,1,2,…,20为货架),转弯半径R为0.8 m。车间选用6辆额定功率为80 W的其技术参数如表3所示,车间各货架的搬运量如表4所示。

图5 车间拓扑图

表3 AGV技术参数

表4 货架的搬运量
3.2 优化方法的有效性分析
首先利用NSGA-Ⅱ算法求解数学模型,关键参数设置如表5所示。

表5 关键参数设置
求解模型得出Pareto解对应的优化目标值如图6所示。
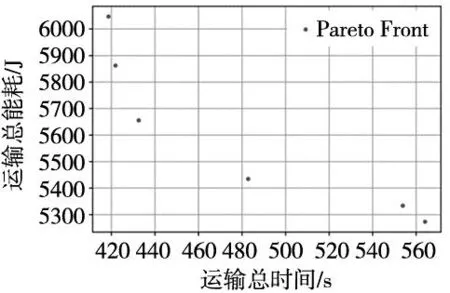
图6 初始节能Pareto集
为对比能耗优化效果,本文选择Pareto解集中对应能耗最低的解进行分析,如表6所示。
分两种情形验证模型节能效果的有效性:情形1下AGV执行运输任务的顺序可优化调整,仅关注搬运时间T。情形2下AGV执行运输任务的顺序可优化调整,综合考虑搬运时间T和总能耗Etotal。求解结果如表7所示。
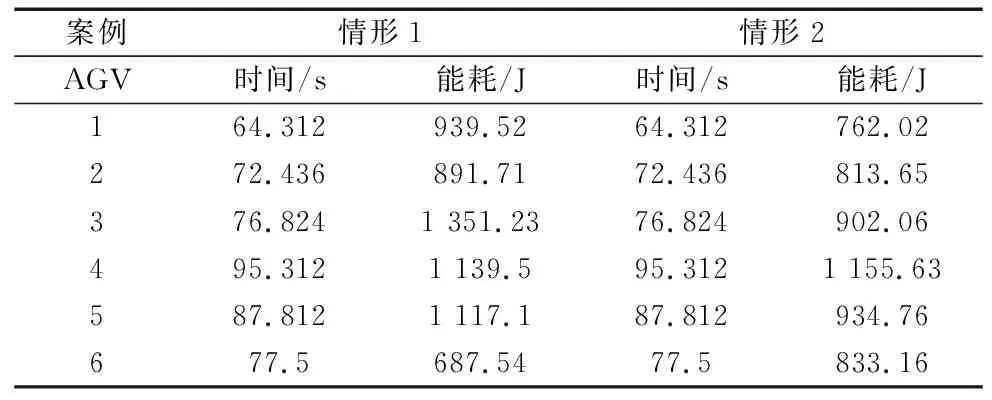
表7 情形对比
两种情形都得到了最短搬运时间,而情形2与情形1相比,能耗降低11.84%。因为情形2综合考虑搬运时间和能耗两个优化目标,在AGV执行运输任务时,加入考虑AGV的能源消耗,得出既能保证搬运效率又能有效降低AGV能耗的搬运路径。
针对多AGV系统进行运输任务时容易发生冲突问题,根据不同冲突类型进行消除。经第一阶段路径规划模型计算得出各AGV的初始节能路径安排如表5所示,得出初始AGV路径时间窗如图7所示,进而第二阶段冲突检测及避撞算法,采用动态优先级策略,结合图3冲突消减流程处理AGV冲突。节点冲突判断的时间阈值δ取2.67 s,α=β=γ=1/3。

图7 初始AGV路径时间窗
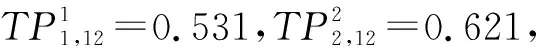

图8 动态优先级策略消减冲突后的AGV路径时间窗
多AGV系统在完成运输任务时易出现冲突问题,故在对模型所得的初始路径进行碰撞调整,由图所知AGV2、AGV4、AGV6执行运输任务的时间未受到优先级策略的影响,尽管AGV1、AGV3、AGV6在执行运输任务的时间有所增加,但是AGV系统总的运输时间并没有发生变化。可知基于动态优先级的策略有效避免了冲突问题,既能做到降低路径上车辆堵塞又能做到提高系统的运行效率。
4 结束语
针对部分连通车间多AGV系统动态无冲突节能路径规划问题,提出两阶段优化方法进行求解,首先建立以搬运时间和能耗为优化目标的多AGV节能路径规划模型,求解出初始节能路径。然后利用时间窗检测冲突类型,构建动态优先级策略进行主动避撞机制。当出现突发情况时,通过被动避撞机制对AGV进行重调度,以规划出全局多AGV无冲突路径。基于案例研究表明:
(1)采用NSGA-Ⅱ算法求解模型,分两种情形进行分析对比,发现在综合考虑搬运时间和能耗的情形下,能够保证搬运时间最短的基础上,同时能耗能够降低11.84%,验证模型的有效性。
(2)分析出AGV系统运输过程中的冲突类型,采用动态优先级策略解决冲突问题可缩短任务完成时间,解决车辆堵塞,该方法灵活简单。在未来工作中可以加入考虑AGV电量情况、充电类型进行规划,获取均衡的冲突解决节能路径。
