基于改进鸡群优化算法的机械臂轨迹规划*

2024-01-03李长勇

组合机床与自动化加工技术 2023年12期

马龙,李长勇,司庆

(新疆大学机械工程学院,乌鲁木齐 830017)

0 引言

随着工业的发展,机械臂在工业领域应用的越来越广泛[1]。机械臂的轨迹规划是机械臂控制领域的研究重点,机械臂轨迹规划分为笛卡尔空间轨迹规划和关节空间规划,笛卡尔空间轨迹规划是对机械臂末端执行器的轨迹规划,而关节空间轨迹规划是对各个关节角度进行规划。目前进行轨迹优化的主要是对关节空间进行轨迹规划,目的包括以下4种:缩短运动时间,降低运动能量,减少关节的运动冲击,以及综合考虑多目的[2]。

当前诸多学者对机械臂的轨迹规划进行了研究,刘贝贝等[3]为了减少冲击和振动对机械臂造成的损害,采用一种5次多项式结合均匀5次B样条的来进行轨迹规划,得到了较为光滑的关节角度、角速度、角加速度关于时间的变化曲线,减少了运动的冲击,但是对时间没有优化,无法提升机械臂工作效率;郝晗等[4]进行了遗传算法的初始种群生成方式、变异算子和交叉算子的构造优化研究,使用3次B样条曲线进行轨迹插值,将改善后的遗传算法运用到轨迹优化中,仿真结果证明该方法有效的缩短了机械臂运行时间,但未考虑机械臂运动中冲击造成振动与磨损的问题;袁旭华等[5]通过增加控制点对三次B样条曲线进行完善,并给出了优化搜索策略蜂群算法的解决途径,提高了曲线拟合准确性,并减少了规划时间,但是机械臂在轨迹起点的初始加加速度不是零且曲线不平滑,会造成机械臂机运动冲击过大;孙颙琰等[6]在传统蝙蝠算法中的局部搜索中加入动态干扰系数,并改进局部搜索和全局搜索策略,使用5次多项式进行轨迹插值,将时间、能耗和冲击设为优化目标,使用改进算法对机械臂运动进行轨迹优化,有效的提高了机械臂的运行效率,但是求解过程复杂,计算耗时长。

目前,机械臂的轨迹优化主要把时间最优或冲击最优作为单一优化目标,机械臂在工厂工作中,要长时间搬运重物,为了提高工作效率、减少关节磨损,综合考虑机械臂运动时间和冲击,进行六自由度机械臂轨迹优化研究。利用5次B样条在关节空间构造插值曲线,并加入鸡群优化算法。将鲸鱼算法与蜉蝣算法融入到鸡群优化算法中,提高算法收敛速度;引入莱维飞行策略,进而提升算法全局搜索能力;引入变异操作,防止陷入局部最优。通过改进的鸡群优化算法对时间和冲击进行优化,规划出关节轨迹,达到缩短时间减小冲击的目标。

1 机械臂运动学分析

为了研究机械臂轨迹规划,对机械臂进行运动学分析必不可少,本文中以埃夫特ER3A-C60型机械臂为研究对象,如图1所示,其拥有6个关节并均为旋转副,能承受较大载荷,可以搬运较重的零件。对机械臂关节建立连杆固连坐标系,如图2所示。

用标准D-H参数法对该机械臂进行模型建立,该机械机器臂D-H参数如表1所示。

表1 D-H参数

使用MATLAB机器人工具箱建立模型,世界坐标系与机械臂的基坐标系相互重合,减少计算量,机械臂在零位时的模型如图3所示,借助搭建的模型,可以验证机械臂正、逆运动学正确性。

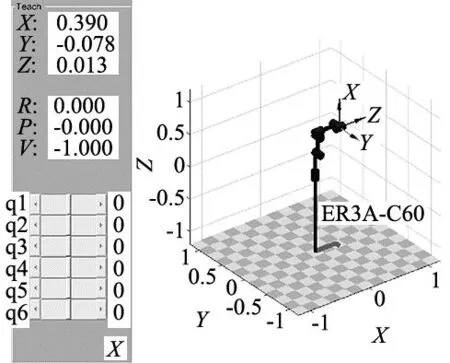
图3 ER3A-C60型机器人模型

1.1 机械臂的运动学分析

(1)

式中:c为cos,s为sin。

(2)

(3)

式中:[n,o,a]3×3表示机械臂末端相对于基坐标的姿态矩阵,[Px,Py,Pz]T表示机械臂末端相对于基坐标的位置矩阵。

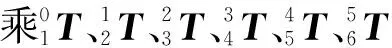
1.2 轨迹规划模型

机械臂在工作过程中执行器末端在笛卡尔空间会通过一系列轨迹点,{oi},i=0,1,…,m,其中o0代表机械臂末端起始轨迹点,om代表机械臂末端终止轨迹点,通过机械臂逆运动学求解,可以推导出轨迹点对应的关节空间位置为{θij},j=1,2,…,n,其中n是机械臂关节的个数[5]。优化目标定义为:

(4)

(5)

式中:F1代表机械臂运动总时间,ti代表从轨迹点oi到oi+1的时间,i=1,2,…,m-1,F2代表机械臂关节冲击。

归一化目标函数如下:

Ff=KtF1+KjF2+KpFp

(6)

式中:Kt为时间系数,Kj为冲击系数,Kp为惩罚项系数,设定Kt=0.4,Kj=0.6,Kp=5;Fp是惩罚项,初始值是0,当关节超过各约束都会使其值增加1。

机械臂运动过程中,需要满足以下约束函数:

(7)

1.3 B样条插值构造

B样条曲线具有较高的灵活性,可以进行局部微小的修改操作,而且各个关节需要满足关节角度、角速度、角加速度和角加加速度的约束,使用五次B样条曲线对机械臂进行轨迹规划插值拟合[7-8],得到角度、角速度、角加速度、角加加速度都平滑连续的函数曲线。B样条曲线方程为:

(8)

(9)

式中:u是变量,di是控制顶点,规定0/0=0;Bi,k(t)是k次B样条基函数,区间u∈[ui,ui+k+1]定义节点矢量U=[u0,u1,u,…,u2k],对于一点ui最多有k+1个非0的k次B样条Br,k(u),其中r∈[i-1,i],其他k次B样条基函数都为0。因此B样条曲线可另外表示为:

(10)

将插值曲线的定义域转换成规范定义域,节点矢量为:

(11)

对时间节点归一化,得到:

(12)

得到满足插值条件的n+1个方程:

(13)

式中:ui+k∈[uk,un+k],i=0,1,…,n。

使用切矢边条件约束可以得到k-1个条件,5次B样条曲线可以得到:

(14)

式中:vs和ve是关节启停速度,as和ae是关节启停加速度。根据德布尔递推公式求出各阶矢导:

(15)

(16)

根据上述公式可得个n+5个方程,以矩阵形式表示:

Ajdj=pj

(17)

(18)

通过式(17)可反推求解出控制点:

(19)

根据式(12)、式(19)、式(9)求出的时间节点向量、控制顶点向量和B样条基函数;由式(10)得到关节在t∈[t0,tn]的轨迹曲线,由式(15)可以得出各阶导曲线,可在求解最优轨迹规划时构造约束函数。

2 鸡群优化算法

常用的轨迹优化算法有遗传算法,粒子群算法等,但上述算法针对多目标优化存在求解精度低,后期迭代速度慢等问题,而鸡群优化算法不需要对问题进行特殊处理,比如不需要引入特殊的编码方式、特殊的交配和突变操作等,有着收敛速度快,收敛精度高的优点,因此本文选用鸡群优化算法来进行机械臂的轨迹优化。

2.1 原始鸡群优化算法(CSO)

鸡群优化算法中种群分为3类:公鸡、母鸡和小鸡,将鸡群按适应度值排序,靠前的NR个是公鸡,最后的NC个是小鸡,剩下的是母鸡;将鸡群分为NR个组,保证每个组中都有一个公鸡,母鸡随机分配到各个组中,与公鸡确立跟随关系;随机选取NH个母鸡,小鸡随机分配到母鸡身边,与母鸡确立母子关系。且不同的种群的位置更新方法不同。若第i只鸡用i表示,d表示解的维度,表示解中的第j维,G表示当前迭代轮数,则表示在第G轮迭代时,第i只鸡在第j维上的位置[9]。公鸡的位置更新方法如式(20)、式(21)所示。

(20)

(21)

式中:N(0,σ2)表示均值为0、方差为σ2的正态分布;k代表不同于公鸡i的另一只公鸡k,f为每只公鸡的最优适应度值,ε为计算机中最小的常数,其作用是防止公式中的分母为0造成无法计算。

母鸡跟随自己组中的公鸡寻找食物,母鸡位置更新方法如式(22)～式(24)所示。

(22)

(23)

S2=exp(fr2-fi)

(24)

式中:R表示区间[0,1]上的随机数,abs()表示取绝对值运算,r1为母鸡i所在组内的公鸡,r2为鸡群优化中除了母鸡i和与其同组的公鸡r1之外的另一只公鸡或母鸡。

小鸡跟随自己的母鸡进行觅食,小鸡的位置更新方法如式(25)所示。

(25)

式中:m表示小鸡i的母亲,F表示小鸡跟随母鸡进行觅食的调节参数,由于小鸡群优化体中的每个个体也存在差异性,因此F为区间[0,2]上的随机数。

2.2 改进的鸡群优化算法(ICSO)

公鸡的位置更新方式呈现正态分布,其随意性造成公鸡错过全局最优解,本文将鲸鱼算法[10]的包围机制和蜉蝣算法[11]的速度机制融入公鸡的位置更新方式中,增强全局搜索能力,ICSO中的公鸡的位置更新方法为:

(26)

(27)

S=2Ab2-A

(28)

(29)

(30)

基于莱维的运动方式是非破坏觅食环境中觅食者最佳搜索方法[12],为了使母鸡和小鸡可以更精准的模仿鸡的觅食,引入莱维飞行策略,进而提升算法全局搜索能力。ICSO算法中的母鸡的位置更新方法为:

(31)

(32)

(33)

式中:L(λ)表示莱维飞行产生的步长,β为常数,取值1.5;μ、v为均值为0、方差为1的正态分布;Γ为Gamma函数[13]。

小鸡跟随母鸡,为了增强其全局搜索能力,将小鸡跟随母鸡进行觅食的调节参数替换成莱维飞行步长,ICSO算法中的小鸡位置更新方法为:

(34)

鸡群迭代前期,种群差异较大,但是在迭代后期,个体之间差异程度降低,导致种群多样性降低,致使过早收敛,陷入局部最优。为了优化鸡群优化算法这个缺陷,本文引入随机差分变异操作[14],其定义为:

X(G+1)=Q(pbest-X(G))+Q(X′(G)-X(G))

(35)

式中:Q为差分变异算子,pbest为当前最优个体,X′(G)为群体中随机选出的个体,X(G)为进行变异操作的个体,其作用是对差分值进行缩放。

Q取较大值时,可以让算法搜索范围变广,但是会导致收敛速度减慢;Q取值较小的时候,虽然搜索速度加快,但是会导致陷入局部最优。为了避免上述问题,对差分变异算子进行改进,使算法前期搜索大范围,随着迭代进行加快搜索速度,进后的定义如下:

(36)

式中:M为最大迭代次数,G为当前迭代次数,rand为[0,1]之间的随机数。

鸡群迭代前期,不需要对太多个体进行变异操作,因此,设定前期随机选取变异个体少,随着迭代进行,种群差异变多,增加变异个体,对变异数量的设定为:

(37)

式中:min()为取其中最小值,int表示取整操作,Hm为变异数量上限,定为种群规模的20%。

2.3 ICSO算法步骤

算法基本步骤为:

步骤1:对算法参数初始化,设定鸡群大小N、最大迭代次数M、个体位置维度、公鸡母鸡小鸡的比例;

步骤2:对鸡群进行初始化,将鸡群按适应度值排序,确定公鸡、母鸡与小鸡,并进行分组,确定母鸡与小鸡之间的对应关系;

步骤3:开始迭代,判断是否更新分组,是否跟新集群中的关系,需要则更新;否则公鸡、母鸡与小鸡各自按照式(26)、式(31)、式(34)对自己的位置进行更新,同时计算更新后的适应度值;

步骤4:比较新旧位置适应度值,保留小适应度值的位置;

步骤5:根据式(35)对种群中随机个体进行差分变异操作;

步骤6:判断是否满足迭代停止条件,若是满足。那么算法结束,输出最优解;否则回到步骤3。

2.4 性能测试

为了验证ICSO的有效性,使用MATLAB R2018A平台对ICSO进行性能测试仿真试验,同时添加CSO、WOA两种算法进行对比。设定群数量M为30,最大迭代次数为500次,所有测试函数如式(38)～(43)所示,实验结果如图4所示。

f1=max{|xi|,1≤i≤n},[-100,100]n

(38)

(39)

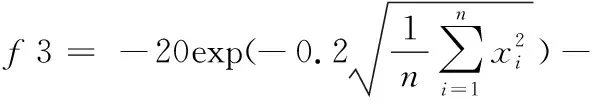
(40)

(41)

(42)

(43)

式中:f1为单峰测试函数,用来衡量算法求解精度;f2、f3为多峰测试函数,用来度量算法全局搜索能力;f4、f5、f6为固定维测试函数,用来测试算法的求解复杂多维能力。

由图4a可知,在求解f1时随着迭代次数的增加,ICSO比WOA和CSO达到更低的函数值,说明ICSO具有更好的收敛精度。由图4b和图4c可知,在求解f2、f3时,起始阶段ICSO就开始快速收敛,并能跳出局部最优,求解f2时ICSO尽管收敛速度比WOA慢,但是能在140次左右达到最优值,且收敛值比WOA低,而CSO收敛速度慢而且收敛值差;求解f3时尽管3种算法收敛值一样,但ICSO在前期能多次跳出局部最优值,最快到达全局最优,体现了ICSO良好的全局寻优能力。由图4d～图4f可知,在求解f4时,ICSO在10次就完成收敛;在求解f5和f6时,ICSO收敛值最低,且不断跳出局部最优解,验证了ICSO的有效性。

图4 测试函数仿真结果

3 实验与分析

为了验证本文提出的ICSO在机械臂轨迹规划中的有效性,以埃夫特ER3A-C60型机械臂为研究对象,使用MATLAB中机器人工具箱对其建模,如图3所示,可通过其中Teach模块控制机械臂运动。机械臂在笛卡尔空间内经过一条轨迹,其中包括起始点和终止点的8个轨迹点对应的各个关节的角度信息如表2所示,将这些关节角度信息记录到电脑中。

表2 轨迹点关节角度

在MATLAB中采用五次B样条,CSO优化和ICSO优化分别对起始点到目标点的共8个轨迹点的的运动轨迹规划仿真对比实验。智能算法迭代次数设置为200次,鸡群数量设置为30,公鸡、母鸡、小鸡的比例为1:2:2,以式(6)中F1、F2为优化指标,得出不同方案下的各关节角度、角速度、角加速度和冲击随时间的变化曲线如图5所示,CSO和ICSO算法轨迹规划收敛曲线如图6所示。

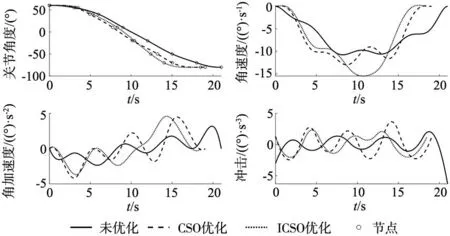
(a) 关节1

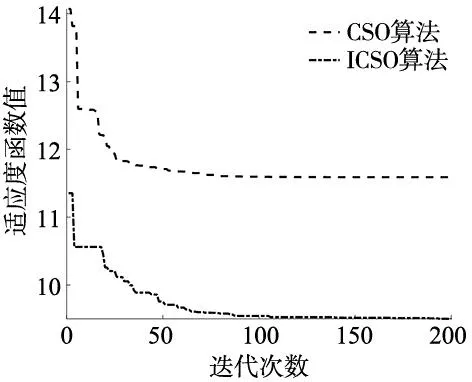
图6 轨迹规划收敛曲线

由图5可知,ICSO收敛值小于CSO,且在迭代20次、40次时均可跳出局部最优。由图6可知,不同方法下规划的曲线都是连续光滑,但能看出经过CSO优化和ICSO优化,机械臂运动时间减少,冲击曲线起伏变小。具体的,各段轨迹运行时间、总运行时间如表3所示,不同方案下关节最大冲击如表4所示。

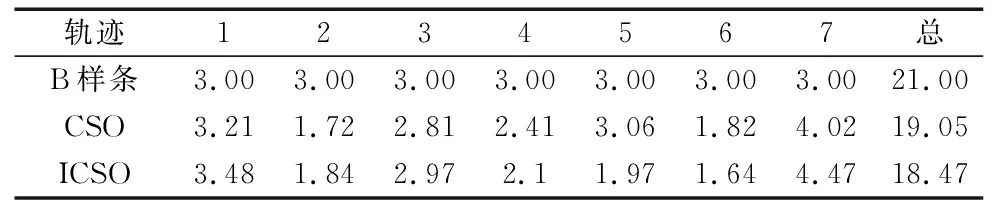
表3 不同方案机械臂运动时间 (s)

表4 不同方案下关节最大冲击 ((°)·s-3)

由表3可知,CSO优化后比B样条轨迹规划的曲线时间减少9%,而ICSO优化后时间减少12%。由表4可知,在经过CSO优化后,比B样条轨迹规划,关节1冲击减少42%,关节2冲击减少66%,关节3冲击减少12%,关节4冲击减少65%,关节5冲击减少67%;而在ICSO优化后,比B样条轨迹规划,关节1冲击减少63%,关节2冲击减少78%,关节3冲击减少25%,关节4冲击减少73%,关节5冲击减少74%。使用CSO和ICSO轨迹优化后关节最大冲击减小,但ICSO效果更优。因此本文提出的ICSO算法不仅降低了机械臂运行时间,还降低了机械臂运动时的冲击,延长了机械臂使用寿命。