三相鼠笼异步电机转子断条故障检测

陈佳炜,陈家新

(东华大学机械工程学院,上海 201600)

0 引言

鼠笼式异步电动机具有结构简单、体积小、价格低廉、坚固耐用等特点,广泛应用于工业生产。随着技术的发展以及电气自动化程度的提高,电机运行环境也越来越复杂,电机一些不合理的结构设计和生产制造上的缺陷,都会导致电机出现故障,使生产效率降低。而在电机的诸多故障中,转子导条断裂约占电机总故障率的10%。因此对转子断条故障进行检测,具有重要意义。

关于转子断条故障检测技术的研究,传统非侵入式电机电流信号分析 (motor current signal analysis,MCSA)方法是目前最常用的故障检测方法,当电机出现转子断条故障时,定子电流中会出现频率为(1±2s)f1的转子断条故障分量,对其进行频谱分析即可诊断转子断条故障。但是,当电机空载或轻载运行时,转差率s极小,转子断条故障分量频率和基波频率很接近,且转子断条故障分量幅值与基波幅值相比极小,导致转子断条故障分量易被基波及噪声所淹没。为了解决上述问题,马宏忠等[1]提出Hilbert模量分析方法,即通过Hilbert变换把定子电流中的基波分量转换成直流分量,将频率为(1±2ks)f1故障成分转换成2sf1和4sf1的低频分量,最后通过频谱来诊断转子断条故障。王臻、阳同光等[2-3]为解决传统Hilbert模量诊断方法频谱过于复杂的问题,提出通过瞬时无功功率来诊断转子断条故障。ZANDI、MALEKPOUR等[4-8]将自适应滤波技术运用于转子断条故障诊断,以此抵消基波信号对断条故障的干扰。张雅晖、许允之等[9-11]则提出将小波包分析和应用于转子断条故障的诊断。

然而,目前大多数研究均在电机负载运行状态下检测转子断条故障,并且未考虑所提取的转子断条故障分量的正确性。针对上述问题,本文提出了需要设置初始有效阶数的基于奇异值增长率的SVD-Prony算法[12-15],用于提取空载低压运行状态下的转子槽谐波及转子断条故障分量。仿真结果表明,所提方法不仅能精确计算电机转速,而且可以验证所提取的转子断条故障分量的正确性,提高了转子断条故障的诊断能力。

1 转子断条故障特征及转子槽数计算公式

一般情况下,鼠笼异步电机定子电流频率和电源频率f1一致,当出现转子导条断裂故障时,定子电流频谱中会出现与f1相差2倍转差频率±2sf的转子断条故障分量。

电源频率表达式为:

(1)

式中:p为电机极对数,n1为电机同步转速。

则二倍转差频率表达式为:

(2)

式中:nr为转子转速。

由于异步电机中的定转子齿槽的存在,会使气隙磁通受到影响,使气隙磁导变得不均匀,导致转子槽谐波磁场的产生。转子槽谐波存在于定子电流以及定子电压,仅和转子槽数Z2有关。转子转速与转子槽谐波频率fRSH关系表达式如下:

(3)

式中:fr为转子频率,K2=±1,±2,…,Z2为转子槽数,α=±1,±2,…。

则转子断条故障分量频率与转子槽谐波频率关系表达式为:

(4)

在未知电机转子槽数时,可使电机运行在空载(380 V)下,此时,nr约等于电机同步转速n1。可从定子电流中提取一对转子槽谐波分量,频率分别为fRSH,1,FRSH,2,并且fRSH,1-fRSH,2=100 Hz。对应频率为fRSH,1的转子槽谐波分量的α=1,频率为fRSH,2的转子槽谐波分量的α=-1,则可计算得整数倍转子槽数K2Z2,如式(5)所示。

(5)

以Y160M-4型鼠笼异步电机作为研究对象,电机相关参数值如表1所示,转子槽数为26。

表1 Y160M-4型电机参数

在空载条件(380 V)下进行二维瞬态电磁场有限元仿真,并分析定子电流FFT频谱,获取转子槽谐波分量。仿真时长1.5 s,采样率5000 Hz,获取稳态下的1 s数据进行分析。如图1所示,在未知电机转子槽数时,利用转子槽数倍率的整数特性,根据式(5)以及频率为1248 Hz和1348 Hz的转子槽谐波,可得K2Z2=52。

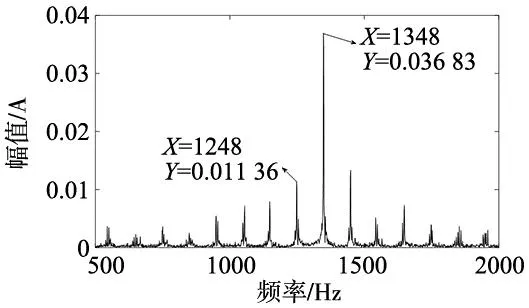
图1 空载定子电流FFT频谱

根据式(4),当转差率过小时,转子断条故障分量频率与基波频率非常接近,容易被基波淹没。因此提出在空载低压运行状态下检测转子断条故障分量,在此状态下,转差率偏大,转子断条故障分量频率偏离基波分量,容易提取。此外,根据空载运行状态下计算所得的K2Z2及式(4)即可计算得到标准转子断条故障分量频率,然后,设定相应频率误差阈值,从定子电流中提取实际转子断条故障分量。

根据式(3)可得,转子槽谐波频率的精度决定了电机转速的计算精度,继而影响转子断条故障分量频率的精度,因此,在提取转子槽谐波及转子断条故障分量时,需使用频率分辨率更高的信号处理算法。

2 SVD-Prony算法理论模型

以下通过基于奇异值增长率的SVD-Prony算法获取转子槽谐波及转子断条故障,Prony算法频率分辨率很高,但其对于噪声较为敏感,易受噪声信号的影响,而电网系统中包含着大量噪声,决定通过SVD来滤除定子电流中的噪声信号。

将采样信号x[n]表示为:

x[n]=z[n]+c[n],n=1,2,…,N

(6)

式中:N为采样点数,z[n]和c[n]分别为定子电流信号和噪声信号。

采样信号构造的 Hankel 矩阵为:

(7)

式中:M+L=N+1,对矩阵R进行奇异值分解。

R=UΣVH

(8)

式中:U,V分别为矩阵R的左奇异矩阵和右奇异矩阵,Σ是M×N阶对角阵,其主对角元素σ1≥σ2≥…≥σh≥0,称为R的奇异值。

奇异值σi是矩阵R的信号的体现,Σ中前k个大的奇异值表现为有效信号,后续较小的表现为噪声。将后续较小的奇异值置为0,则将Σ置0后的矩阵记为Σk,可得R(k)如式(9)所示。取矩阵R(k)的第一行和最后一列,首尾相连,重构信号,即可得到滤除噪声后的信号。

(9)

对于采样信号来说,若定义的有效阶次k过小,即便能滤除大部分噪声信号,但是还会有部分有效信号丢失。若有效阶次k过大,则不能很好的去除噪声信号。因此需要一种方法,能够有效的、自适应的去获取有效阶次k,才能更好的滤波。

从SVD理论可知,非零奇异值个数与矩阵的秩是相等的。无噪信号所构成Hankel矩阵是病态的,矩阵的秩r远小于min(M,L)。因此只有前r个非令奇异值,后续皆为0,在第r个奇异值处会出现转折。对于噪声信号,由其构成的Hankel矩阵相邻行不相关,矩阵是良态的,矩阵的秩r=min(M,L),并且其奇异值大小相等。因此对于理想带噪信号来说,存在第k个奇异值,奇异值序列在此处出现明显转折,奇异值大小急剧下降,后续则趋于平滑。因此可以通过奇异值增长率曲线来寻求相应的奇异值转折点,以此自适应的确定有效阶次k。

(10)

因定子电流成分非常复杂,除了基波分量,还会存在很多谐波成分,当谐波次数很高时,高次谐波成分幅值会与噪声幅值接近,并且基波能量占比很大,导致所期待的ki所代表的奇异值突变点无法出现。因此,提出设置初始有效阶次n,然后在n+1～h区间下寻找奇异值增长率中最大的ki,以此确定最终有效阶次k,如式(11)所示。

(11)

经SVD滤波后的信号为y(n),假设y(n)由任意p个模式的指数函数线性组合而成,表示如下:

(12)

式中:Ri=Aiejθi,zi=exp(-δi+j2πfi)Δt,Ai为幅值,n=0,1,…,N-1,θi为相位,δi为衰减因子,fi为频率,Δt为采样时间间隔。

其平方误差ε为:

(13)

令ε最小即可求出{Ai,θi,δi,fi},为了求解非线性最小二乘法问题,考虑使用常系数线性微分方程,因此式(12)即为式(14)的齐次解。

(14)

(15)

求解该方程得到系数{ai,εp},根据ai系数求解多项式1+a1λ-1+…apλ-p=0,解得λi,以此求出衰减因子δi和频率fi。

(16)

然后,式(12)可简化为以Ri为未知参数的线性方程为:

(17)

则幅值Ai和相位θi分别为:

(18)

3 有限元仿真研究

为了确保最终有效阶次所代表的信号分量包含转子槽谐波及转子断条故障分量,提出如下流程。流程Ⅰ目的为提取转子槽谐波,流程Ⅱ目的为提取转子断条故障分量。

流程Ⅰ:①通过FFT频谱提取转子槽谐波分量,保存其频率fRSH-FFT。②设定初始有效阶数n,并进行SVD分解,根据奇异值增长率曲线及式(11)获取并保留最终有效阶数k,并根据最终有效阶数k重构定子电流信号,通过Prony算法辨识去噪后的定子电流信号;③设置频率误差阈值为FFT频率分辨率/2。对比Prony辨识结果与先前保存的转子槽谐波的频率,若Prony辨识结果中存在频率接近fRSH-FFT的信号成分,且频率误差小于FFT频率分辨率/2,则初始有效阶数n设置正确,保存Prony辨识得到的转子槽谐波频率。若不存在,则将下一流程的初始有效阶数n设置为上一个流程的步骤②中保留的最终有效阶数k,重复步骤②～③;

流程Ⅱ:①在知晓转子槽谐波后,计算得转子断条故障分量频率;②根据上述最终有效阶数k重构定子电流信号,设置频率误差阈值为0.2 Hz,在Prony辨识结果中寻找与步骤4中所计算转子断条故障分量频率接近的信号成分,且频率误差小于0.2 Hz,保存Prony辨识得到的转子槽谐波及转子断条故障分量,并结束流程。若不存在,则重复步骤②,不同的是,需将上一流程步骤②中的最终有效阶数设置为该流程的初始有效阶数,并以此重新生成最终有效阶数来重构定子电流。

以Y160M-4型电机为研究对象,设置转子1根断条,线电压区间170 V～242 V,间隔18 V,负载转矩0。设定仿真步长为 0.000 2 s,仿真时间为1 s。

图2a展示了正常情况下Y160M-4型电机的Maxwell 2D有限元模型,图2b则表示该型号电机一根转子断条故障Maxwell2D有限元模型,图中淡红色的转子导条则代表导条断裂。

(a) 健康电机 (b) 一根断条电机图2 Y160M-4电机模型

以线电压为170 V下的转子断条故障分析为例,根据上述所提流程对定子电流进行分析。

(1)根据FFT频谱获取转子槽谐波频率,如图3所示,转子槽谐波频率为1332 Hz和1232 Hz。

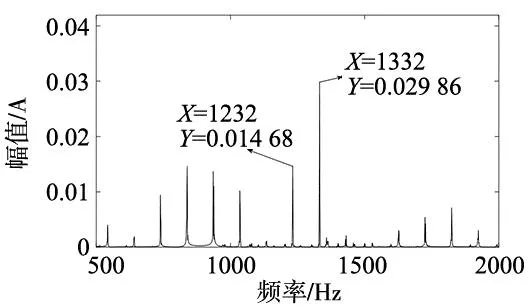
图3 170 V空载定子电流FFT频谱

(2)设置初始有效阶数为12,如图4所示,流程Ⅰ经1次循环,最终有效阶数分别为22。如图5所示,在有效阶数为22的Prony辨识结果中寻找到转子槽谐波频率为1 332.267 1 Hz。

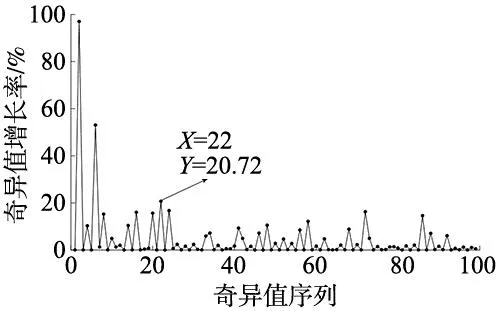
图4 奇异值增长率曲线

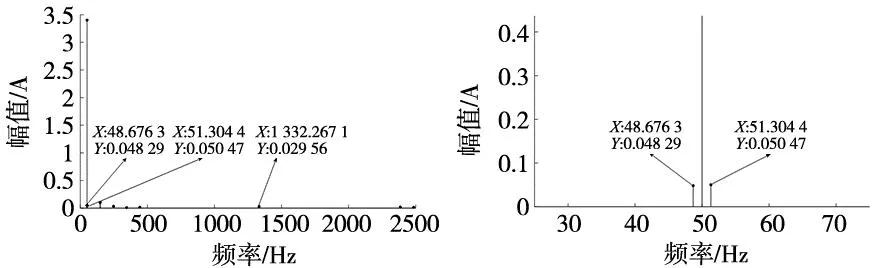
(a) Prony辨识结果 (b) 转子断条故障分量(局部放大)图5 Prony辨识结果

(3)在获取到转子槽谐波后,根据式(4)计算可得转子断条故障分量频率为51.364 1 Hz、48.635 9 Hz。以此为标准在有效阶数为22的Prony辨识结果中寻找转子断条故障分量,如图5所示,转子断条故障频率为48.676 3 Hz、51.304 4 Hz,误差小于0.2 Hz,转子断条故障分量验证正确,表明存在转子断条故障。

测试结果如表2所示。可以发现,在空载低压运行状态下,所提方法不但可以精确计算电机转速,而且可以验证所提取的转子断条故障分量的正确性,更加准确的诊断转子断条故障。

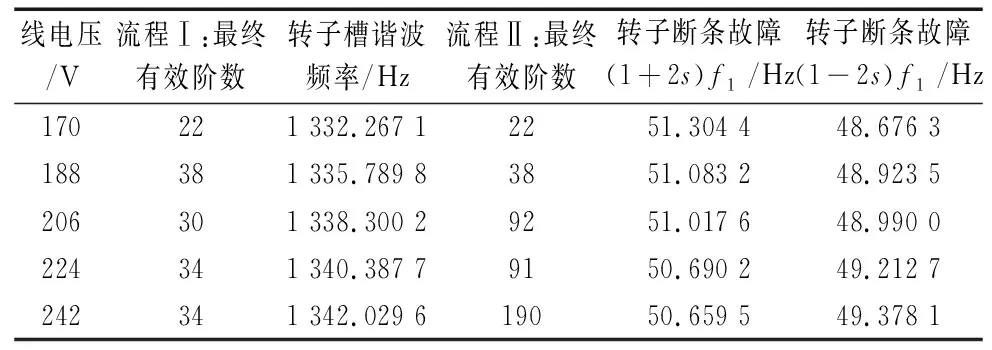
表2 低压空载运行下测试结果

4 结论

本文基于转子断条故障特征及转子槽谐波测速机理,给出了整数倍转子槽数的理论计算公式及转子断条故障分量频率与转子槽谐波频率的关系表达式,并提出了需要设置初始有效阶数的基于奇异值增长率的SVD-Prony算法,用于提取转子槽谐波及转子断条故障分量。通过对三相异步电机在空载低压运行状态下的转子断条故障分析,表明所提方法不仅能精确计算电机转速,而且可以验证所提取的转子断条故障分量的正确性,减少了转子断条故障误判的可能性,提高了转子断条故障的诊断能力。