两自由度电液振动台随机波形复现控制*
2024-01-03王志超关广丰王海涛
王志超,关广丰,熊 伟,王海涛
(大连海事大学船舶与海洋工程学院,大连 116026)
0 引言
电液振动台广泛用于大型结构件的振动环境模拟试验,可以在实验室内复现实际工况下产品所受的振动环境和环境效应,鉴定产品的环境适应性[1]。许多产品在工作环境中受到的振动形式以随机振动为主,所以研究振动台时域随机波形复现具有重要意义。
在波形复现控制系统中,两自由度电液振动台控制系统由伺服控制系统和振动控制系统两部分组成。伺服控制系统利用极点配置原理通过三状态控制等方法,拓展系统频宽,提高系统稳定性[2]。但仅应用伺服控制时,受到系统频宽及非线性特性的影响,系统的响应信号与参考信号会有较大的偏差[3]。为了更好的复现参考信号,要在系统内环伺服控制的基础上外环设计振动控制系统。
振动控制系统主要对伺服驱动信号迭代,进一步减小系统响应误差。UNDERWOOD等[4-5]详细介绍了振动控制的理论基础和核心算法,并通过电液振动台进行实验验证。MOTEN等[6]提出基于自适应逆控制和迭代学习控制的复合控制算法,用于振动台时域波形复现实验。EKSTEEN等[7]提出基于非线性逆模型的迭代学习控制器用于波形复现算法。NAJAFI等[8]在进行地震台模拟实验时,外环通过离线迭代控制对系统驱动信号不断修正来提高加速度信号时域跟踪效果。陈广初等[9]在多输入多输出随机振动实验中引入牛顿迭代算法对驱动信号迭代,使信号功率谱密度达到控制要求。ZHANG等[10]引入Underwood提出的自适应迭代控制方法用于振动台台阵系统的随机波形复现实验。GUAN等[11]引入拟牛顿算法中的Broyden算法和DFP算法,考虑系统耦合时变影响,实时更新系统阻抗矩阵。其中,通过DFP算法可以较好的实现两自由度振动台系统的随机波形复现,但由于迭代中采用固定步长以及算法本身收敛性的限制,随机波形复现精度还有待提高。
目前对于电液振动台时域波形复现的研究已取得很多成果,但仍存在一些不足。当时域上采用自适应逆控制等方法时系统辨识难以消除频响函数存在的抖动特性;而采用频域自适应算法迭代过程多为离线迭代,无法实时更新系统频响函数,并且频域迭代步长一般取定值,而实际过程中步长会随迭代的进行发生变化。另外,上述拟牛顿算法本身不能严格保证迭代中海森矩阵的正定性,使算法的收敛性受到影响。
为解决上述拟牛顿算法中海森矩阵迭代时出现奇异矩阵而影响收敛精度的问题,引入PSB拟牛顿算法进行海森矩阵的迭代。PSB算法在Broyden算法的基础上进行矩阵变换,使海森矩阵具有对称正定的性质,保证了迭代过程的强收敛特性[12]。针对频域迭代步长变化的特性,引入自适应变步长算法,进一步加快迭代收敛过程。本文首先给出两自由度电液振动台基本结构,介绍振动控制系统基本组成,简要分析传统控制算法的不足,然后给出PSB算法的基本原理,并推导出以PSB算法为基础的频域驱动谱迭代公式,结合自适应变步长公式,设计随机波形复现控制器。基于两自由度电液振动台,进行控制系统仿真及实验,验证该控制算法的有效性。
1 两自由度电液振动台系统概述
两自由度电液振动台结构如图1所示,振动台处在工作准备位置。4组阀控液压缸并联构成驱动系统,通过虎克铰将振动台上平台与下基面连接。下基面固定在地面上,上平台通过连接处的虎克铰可以实现rx和ry两个转动自由度。振动台主要参数如表1所示,在俯视图中用符号d1、d2、d3表示液压缸在下基面的位置,分别为0. 8m、0.7 m、0.4 m。其中,d1表示1号(3号)和2号(4号)液压缸上铰点中心的距离在Y轴上的投影;d2表示1号(2号)液压缸上铰点中心和虎克铰中心的距离在X轴上的投影;d3表示3号(4号)液压缸上铰点中心和虎克铰中心的距离在X轴上的投影。

表1 振动台主要参数
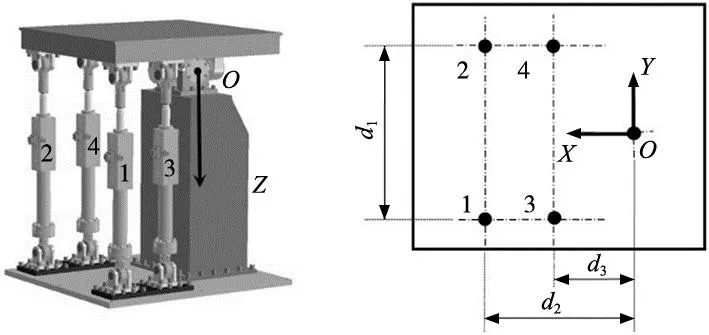
(a) 三维模型 (b) 俯视图图1 二自由度电液振动台工作准备位置结构
2 随机波形复现控制器设计
2.1 PSB广义阻抗更新算法
图2为波形复现振动控制策略基本原理流程框图。图中,两自由度电液振动台伺服控制器结构可参考文献[13]。振动控制算法主要包含初始阻抗辨识、阻抗矩阵迭代、驱动谱迭代三部分。控制系统的原理是通过系统的频响函数,对系统驱动信号进行多次循环迭代补偿,使系统的响应信号与参考信号误差修正后在一定允许范围内。
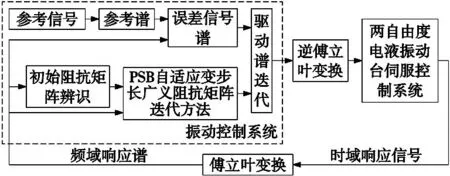
图2 随机波形复现振动控制策略基本原理图
设振动试验参考信号为r(t),其频谱为R(f);系统时域驱动信号为d(t),频谱为D(f);时域响应信号为c(t),频谱为C(f);误差信号谱为E(f),即E(f)=R(f)-C(f);系统频响函数矩阵为L(f),阻抗矩阵为Z(f),则存在关系Z(f)=L-1(f)。
传统波形复现控制算法驱动谱迭代公式为:
Dn+1(f)=Dn(f)+δnZ(f){R(f)-Cn(f)}
(1)
式中:δn为迭代步长,n为迭代次数,Dn(f)为迭代第n次时的信号驱动谱,Cn(f)为迭代第n次时的信号响应谱。
在传统波形复现算法中,系统不更新阻抗矩阵Z(f)。而实际系统中阻抗矩阵具有时变特性,导致估计得到的阻抗矩阵与系统真实阻抗矩阵始终存在误差。在驱动谱迭代过程中,误差不断累积放大,多次迭代后可能导致系统发散。
采用PSB拟牛顿算法对阻抗矩阵进行更新,PSB算法迭代公式为[14]:
(2)
式中:上标T表示复向量的转置,Bn及Bn+1分别表示采用PSB算法迭代第n次及第n+1次后的海森矩阵,Sn为每次驱动谱迭代增量,Yn为迭代梯度差。即存在关系:Sn(f)=Dn+1(f)-Dn(f)、Yn(f)=Cn+1(f)-Cn(f)。
考虑采用迭代海森矩阵Bn替换系统阻抗矩阵Z(f)进行实时更新。但在拟牛顿算法迭代过程中,每次迭代都要对海森矩阵求逆,求逆矩阵的过程带来很大的运算量,降低算法迭代收敛速度。引入Sherman-Morrison-Woodbury公式[15]对式(2)变换,得到新的PSB算法迭代公式为:
(3)
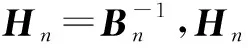
(4)
式中:上标H表示复向量的共轭转置。将广义阻抗矩阵Pn(f)替换传统迭代阻抗矩阵Z(f)可得到新的驱动谱迭代公式为:
Dn+1(f)=Dn(f)+δnPn(f){R(f)-Cn(f)}
(5)
式(5)中,应用迭代公式(4)对广义阻抗Pn(f)迭代。
2.2 自适应变步长算法
文献[16]中利用L2范数来描述多输入多输出控制系统的误差信号谱。基于随机波形复现算法,定义两自由度电液振动台随机波形复现控制优化问题的目标函数为:
(6)

为了得到最优驱动谱D(f),需要寻找最优迭代步长δn使F[D(f)]最小,且满足迭代条件F[Dn+1(f)]≤F[Dn(f)]。假设控制系统为全纯的,则存在关系:
Cn+1(f)-Cn(f)=L(f){Dn+1(f)-Dn(f)}
(7)
将式(5)代入式(7),可得:
Cn+1(f)-Cn(f)=δnL(f)Pn(f){R(f)-Cn(f)}
(8)
由式(8)可得控制响应谱更新公式为:
Cn+1(f)=Cn(f)+δn{In+ΔLn(f)}En(f)
(9)
式中,En(f)=R(f)-Cn(f),ΔLn(f)为当前迭代时阻抗矩阵估计误差,In为单位矩阵。
若目标函数F[D(f)]为近似厄米特二次型且系统为全纯的,将目标函数对δn求复微分,可得自适应变步长公式为:
(10)
εn(f)={In+ΔLn(f)}En(f)
(11)
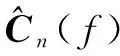
(12)
(13)
(14)
3 仿真分析
3.1 仿真设定
图3为基于PSB自适应变步长控制算法搭建的随机波形复现仿真模型,与图2振动控制策略原理图各部分相对应。其中,广义阻抗迭代部分用来实现式(4)。通过式(13)实现自适应变步长的更新,使驱动谱迭代分为定步长和自适应变步长两步迭代,分别实现式(12)和式(14)。
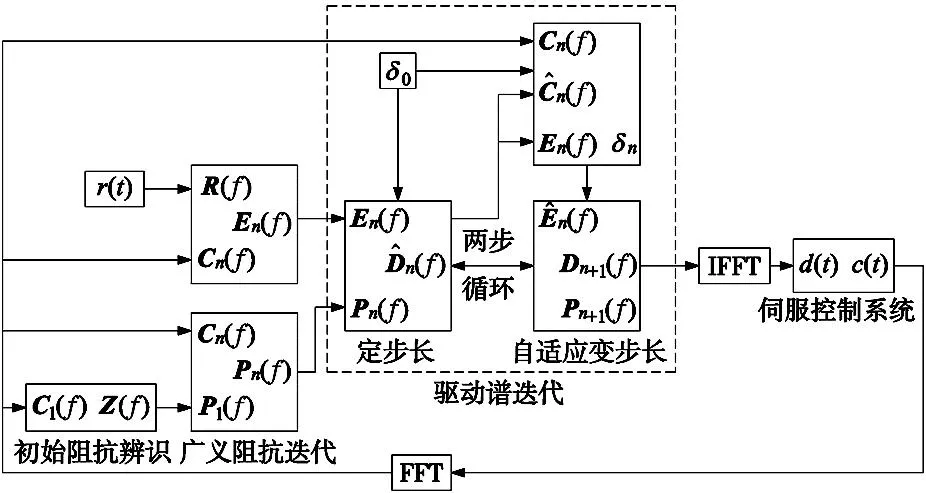
图3 随机波形复现控制算法仿真模型
基于MATLAB/Simulink进行DFP定步长随机波形复现算法和PSB自适应变步长随机波形复现算法仿真。其中,通过H1法辨识得到系统频响函数矩阵初值,求逆得到初始阻抗矩阵,再利用上述两种算法进行广义阻抗矩阵迭代分析。
仿真中设置随机参考信号r(t)的最大峰值为1.2 rad/s2,频带为10~100 Hz,取定步长δ0值为0.7。考虑到实际中振动台系统耦合时变性,为了验证波形复现算法的有效性,仿真程序中设置参数切换模块,在第40次迭代时,通过调整伺服系统内部增益模拟实际系统的频率特性变化。
采用时域波形最大误差评价波形复现精度,计算公式为:
(15)
3.2 仿真结果
分别给出基于DFP定步长算法和基于PSB自适应变步长算法两种情况下两自由度振动台的随机波形复现曲线。
文献[11]中对传统波形复现算法进行仿真,结果表明,当系统频率特性突变后,系统迭代快速发散。图4为频率特性突变前后,两个自由度随机波形复现最大误差走势图。在突变之前,两种波形复现算法的迭代过程都逐渐收敛。其中,第25次迭代时,DFP定步长算法rx自由度Emax为43%,ry自由度Emax为38%;而PSB自适应变步长算法rx自由度Emax为25%,ry自由度Emax为16%。PSB自适应变步长算法波形复现误差更小。系统增益耦合突变后,DFP定步长算法需经过6个迭代周期,系统才收敛至稳定;而PSB自适应变步长算法经过3个迭代周期,系统快速收敛达到稳定状态。PSB自适应变步长算法收敛速度更快。

(a) rx自由度 (b) ry自由度图4 波形复现最大误差仿真结果
第60次迭代时,采用两种算法均已再次收敛,分别给出其波形复现曲线。图5为采用DFP定步长算法时两个自由度的波形响应,其中rx自由度Emax为8.2%,ry自由度Emax为5%。图6为采用PSB自适应变步长算法时两个自由度的波形响应,两个自由度的Emax均小于3%。PSB自适应变步长算法波形复现精度更高。
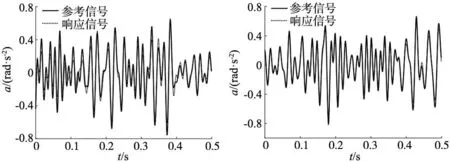
(a) rx自由度 (b) ry自由度图5 DFP定步长算法波形复现仿真结果
4 实验研究
应用图7所示的两自由度电液振动台实验系统进行随机波形复现实验研究,在仿真基础上进一步验证控制算法的有效性。振动台参数如表1所示。两自由度电液振动台系统由恒压式变量泵供油。在每组液压缸上均安装传感器测量系统位移、速度及加速度。振动台控制系统软件基于MATLAB/XPC平台构建。控制系统算法执行周期为1.2 ms。实验中每4帧信号作为一次迭代进行。两自由度加速度随机波形信号应用MATLAB预先生成,并作为参考信号输入实验系统。rx和ry两个自由度的随机波最大峰值分别为2.3 rad/s2和3.0 rad/s2,实验频带为5~50 Hz。实验中初始定步长δ0数值同样设置为0.7。

图7 两自由度电液振动实验台
实验时,分两组进行实验研究。第一组采用DFP定步长算法,第二组采用PSB自适应变步长算法。为方便观察分析实验结果,选取一次迭代中的500个频率点数据做出实验曲线。
分别计算两组实验中每次迭代最大误差并作出曲线,如图8所示。实验中在系统收敛稳定后第15次迭代时调整系统总增益,可看出波形复现误差会有一个突变,经过2次迭代可再次收敛回来。与采用DFP定步长算法相比,采用PSB自适应变步长算法随机波形复现最大误差明显降低。

(a) rx自由度 (b) ry自由度图8 波形复现最大误差实验结果
同时,给出系统收敛稳定后第12次迭代时,两组实验的随机波形复现曲线。图9为采用DFP定步长算法的波形复现曲线,其中rx自由度Emax为26.5%,ry自由度Emax为24.2%。图10为采用PSB自适应变步长算法的波形复现曲线,其中rx自由度Emax为15.4%,ry自由度Emax为12.1%。可看出第二组实验中,采用PSB自适应变步长算法波形复现效果更好。
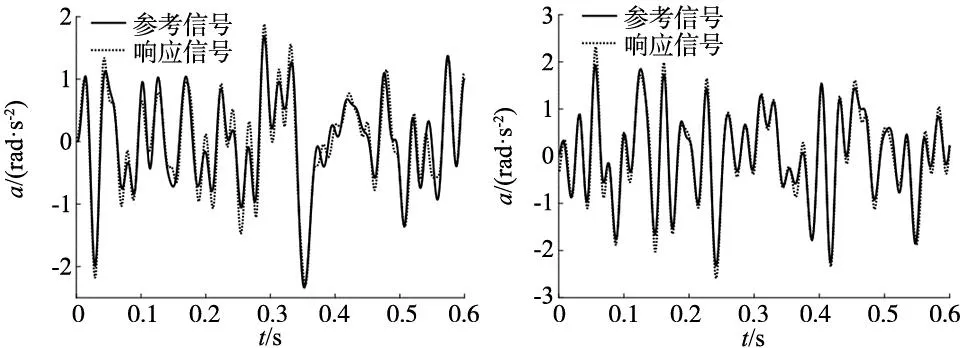
(a) rx自由度 (b) ry自由度图9 DFP定步长算法波形复现实验结果
5 结论
针对两自由度电液振动台受负载特性变化等因素影响时域随机波形复现精度的问题,提出了基于PSB自适应变步长的波形复现控制算法,对驱动谱广义阻抗矩阵实时迭代更新。基于MATLAB/Simulink平台搭建振动台控制系统仿真模型,设计了PSB自适应变步长算法控制器。实验研究表明,采用PSB自适应变步长算法进行两自由度随机波形复现时,rx自由度加速度时域最大误差为15.4%,ry自由度加速度时域最大误差为12.1%。与DFP定步长算法控制器比较,PSB自适应变步长算法控制器具有更强的迭代收敛特性,能够实现两自由度电液振动台加速度随机波形的高精度复现。
由于实际电液振动台系统具有较强的非线性特性,导致实验结果与基于线性模型的仿真结果相比存在一定的偏差,后续将继续开展基于振动台非线性模型的随机振动控制方法研究。
