基于POE和CSSA的冗余机械臂逆运动学求解方法

黄振宇,姜勇

(1. 沈阳理工大学 自动化与电气工程学院,辽宁 沈阳 110006;2. 中国科学院 a. 网络化控制系统重点实验室; b. 沈阳自动化研究所,辽宁 沈阳 110016;3. 中国科学院 机器人与智能制造创新研究院,辽宁 沈阳 110169)

0 引言

传统串联机械臂通常采用D-H参数法[1]来建立机械臂的运动学模型。D-H参数法需要在机械臂各个关节处建立关节坐标系,然后得到每一个关节坐标系相对于前一个关节坐标系的齐次变换矩阵,将得到的齐次变换矩阵按照关节的顺序连乘,即得到机械臂的正向运动学方程。赵志亮等[2]利用D-H法建立7自由度仿人机械臂正运动学方程对其工作空间进行分析。哈佛大学教授ROGER Brockett最先开始将机械臂的运动使用旋量的几何特性映射来进行描述,进而形成了一种机械臂基于指数积的建模方法,通常也将这种方法称为指数积公式。随着大量学者使用指数积公式在机器人领域进行广泛应用和深入研究,该方法也越来越成熟。吴亮等[3]采用旋量法建立机械臂正运动学方程进行运动学分析。相较于传统的D-H参数建模法,使用旋量指数积公式建模法来描述机器人的运动具有两个方面的优势:一是该方法在建模中只用到基础坐标系和工具坐标系这两个坐标系,并且能够对转动关节和移动关节利用相同参数进行统一描述,具有很好的通用性;二是运动螺旋能够将机械臂运动的几何意义完整且清楚地描述出来,有利于避免机械臂出现奇异性问题。

相较于传统6自由度机械臂来说,冗余机械臂因其自由度的增加使得计算运动学反解的难度也随着增加。文献[4]中使用Paden-Kahan子问题法对工业机械臂进行逆运动学求解。该方法是一种运动学逆解问题的几何算法,其利用正向运动学解映射的指数积公式进行构造。使用这种方法通常可以得到一个或两个精度较高的封闭解,可是面对冗余度机械臂逆解的无穷性子问题法将遭遇较大的困难。冗余机械臂由于其具有复杂的耦合性,为了求解机械臂的逆解,文献[5]采用牛顿拉普森数值迭代法求解近似逆解。对于特定结构的仿人机械臂手臂,赵志亮等提出了一种7自由度机械手模型的参数化逆运动学解,讨论了如何表示机械臂的冗余,然后进行运动学分析,推导出机械臂的参数化逆运动学解。针对传统方法在机械臂逆运动学求解问题中的不足,许多学者也试着将一些智能算法[5-10]应用到逆运动学求解中,其优点在于求解不受机械臂构型的限制,具有较强的通用性。

本文以具有S-R-S构型的7自由度冗余机械臂为研究对象,提出一种7自由度仿人机械臂的逆运动学求解方法。首先基于旋量指数积法建立机械臂正运动学方程;然后,采用一种改进的混沌麻雀搜索算法[11]求解运动学逆解,该算法引入高斯变异和混沌序列使其搜索精度提高并且防止陷入局部最优解;最后在MATLAB上编程实现反解算法进行验证,将求出的逆解利用旋量指数积建模法画出的机械臂位姿进行验证。重复进行实验,统计机械臂实际末端位姿与预期位姿之间的误差并进行分析。

1 基于POE运动学建模

在三维空间中,为了描述刚体的运动,不仅需要描述刚体的位置,还要确定其姿态。在旋量理论中,刚体在空间中的所有运动都可以通过绕某个旋转轴的转动加上沿平行于该轴线的移动得到。

假设{B}为固连在机械臂的坐标系,称其为本体坐标系,{A}为空间坐标系,称其为基础坐标系,且都是笛卡儿空间坐标系。定义3×3的矩阵

R=[x,y,z]

(1)

式中:x,y,z∈R3,是本体坐标系相对于基础坐标系的方向矢量;R是一个旋转矩阵,用来描述本体坐标系与基础坐标系的相对姿态变化。R∈SO(3),属于李群元素,具有如下性质:

RRT=RTR=I,detR=1

(2)

式中I为3×3的单位矩阵。

向量P∈R3为一个三维向量,位置矢量用来描述本体坐标系与基础坐标系的相对位置变化。结合姿态矩阵和位置矢量可以组成一个位姿矩阵T=(R,P)∈SE(3),写为齐次矩阵形式如下:

(3)

机械臂各关节运动均可看作旋量运动,取各关节轴向矢量为ω∈R3,取各关节轴线上一点r∈R3,则其运动旋量ξ为

(4)

(5)

刚体的旋量运动若以矩阵指数的形式来表示,则有

(6)

本文研究的7自由度机械臂具有S-R-S构型。S-R-S机械臂也称为拟人机械臂,通常用作仿人手臂,因为该机械臂的结构与人类手臂相似。如图1所示,7个旋转关节被布置成与人类手臂类似的肩部、肘部和腕部。肩关节(1、2和3)可以视为虚拟球形关节,因为这些关节轴在一个点相交。腕关节(5、6和7)也具有相同的结构。此外,两个相邻的关节轴垂直放置。

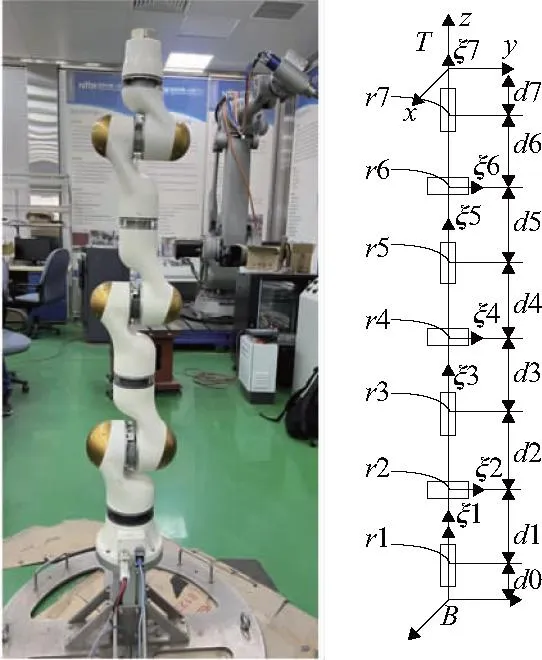
图1 机械臂模型

图2 CSSA算法流程

将坐标系建立在机械臂末端,则工具坐标系T相对于基础坐标系B的位姿矩阵可以由gbt表示,机械臂初始位姿为gbt(0),机械臂的正运动学为

(7)

2 基于CSSA逆运动学求解

机械臂逆运动学求解是已知末端位姿gbt求解关节角θ=(θ1,θ2,θ3,θ4,θ5,θ6,θ7)的过程。本文采用一种改进混沌麻雀搜索算法求解7自由度冗余机械臂的逆解。算法首先设置初始化参数,其中需要初始化的参数有麻雀种群规模N,发现者和跟随者数量比例,目标函数gbt(θ)的维度,最大进化迭代数和求解精度,在关节角度范围内利用佳点集均匀分布的特性初始化种群,生成N个取值范围在(-π,π)内的七维向量Zi。计算种群中每只麻雀的适应度值fi,选出当前最优适应度值和最坏适应度值以及所对应的位置。挑选适应度值较优的前P个个体作为发现者,剩余的麻雀作为追随者,根据公式更新发现者和追随者的位置。一次迭代完成后,重新计算每只麻雀的适应度值fi和麻雀种群的平均适应度值favg。根据当前种群的状态,更新麻雀个体所迭代出的最优和最坏适应度值以及对应的位置。最后判断算法运行是否到达设置的程序退出条件,如果满足其中之一,则循环结束并输出寻优结果,否则继续更新发现者和跟随者的位置进行迭代,直至满足循环结束条件。

发现者位置更新:

(8)

式中:t是当前迭代次数;T是最大迭代次数;α为(0,1]的均匀随机数;Q为标准正态分布的随机数;L为元素均为1的d维向量;R2和ST为阈值和安全值。

跟随者位置更新:

(9)

A+=AT(AAT)-1

(10)

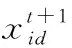
为了计算机械臂实际末端位姿和预期位姿之间的误差,根据位置矢量p和接近矢量a进行加权来构造适应度函数。

(11)

式中:α、β、γ是适应度函数的权重值;θinit为初始关节角;f2为关节角最小变化值。

3 仿真实验

为了检验该算法在求解冗余机械臂逆解的可行性,在MATLAB中进行仿真实验,设置麻雀种群大小都为POP_size=100,最大进化迭代次数MAX_gen=100,适应度函数的权值分别为α=0.001,β=1,γ=0.5。在经过100次迭代之后,其中一组实验适应度曲线如图3所示。

图3 适应度曲线

该次仿真实验中,算法迭代了100次,根据每次计算之后得到最后的适应度,输出最优种群结果即一组关节角值,将S-R-S机械臂配置成肩肘腕的模型,在MATLAB中绘出机械臂的位姿状态(图4)。为了验证其正确性,还将对应的逆解值输入实验室机械臂控制器中,使其点动达到实验的期望位姿,如图5所示。

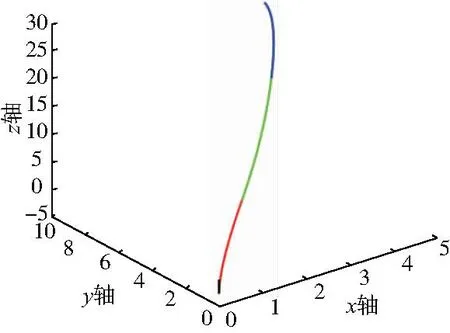
图4 机械臂仿真图

图5 机械臂实验图

此外,本文进行了100次实验,统计了100次实验中机械臂期望位姿与实际位姿的误差,如图6所示。

图6 位姿误差

从图6中可以看出,在100次实验中,实验的位姿误差均为10-4数量级,且有91次实验的位姿误差小于2×10-4。

4 结语

本文运用旋量指数积的方法对一种7自由度冗余机械臂进行正运动学建模,并且进行正运动学分析,这种方法能够清晰地描述机械臂整个系统的运动,简化了机械臂运动学分析的过程,而且它从整体上就可以描述机械臂的运动,从而避免在使用传统方法为机械臂建模时可能产生机械臂关节的奇异性。同时运动旋量与力旋量存在对偶关系,所以有关运动旋量的理论也适用于力旋量,本文建模方法对于后续机械臂动力学分析提供了完备的研究基础。然后本文采用一种改进混沌麻雀搜索算法来对机械臂进行逆运动学分析,求解出机械臂的逆解,这种算法求逆解不需要考虑冗余机械臂的高度耦合特性,并且其计算出的结果经过MATLAB中的仿真验证后,所得到的结果误差可以维持在10-4数量级。