数控系统中S型曲线加减速控制算法研究
2024-01-03刘远凯
刘远凯
(深圳众为兴技术股份有限公司,广东 深圳 518052)
0 引言
在数控运动控制系统中,加减速控制算法直接影响着运动控制系统的实时性、稳定性与加工精度等。可通过加减速控制算法对待加工轨迹段位移、速度、加速度和加加速度曲线进行合理规划,实现在启动、停止、加速和减速运动阶段对系统的柔性控制,避免系统产生失步、震动、超程等现象,保证系统高速平稳运行。
对于柔性加减速控制算法,国内外学者已经进行了探讨。郭新贵等[1]利用三角函数构建加减速曲线,减少了在进给过程中的柔性冲击问题;冷洪滨[2]建立了五次多项式的加减速控制模型,具有速度曲线、加速度曲线和加加速曲线均连续的特性;李明等[3]利用切比雪夫多项式逼近正弦函数方法,构造了一种加加速连续的加减速算法。上述的算法研究与S型加减速曲线相比,具有更高阶的连续性,但速度规划的复杂程度却大大提升,有些甚至都不能实现。因此这些加减速算法在实际工程应用中并不多。
S型加减速控制算法因其速度曲线和加速度曲线均具有连续性,成为当前数控系统中使用较多的一种速度控制算法[4-6]。S型加减速因其实用性,也受到了很多学者的关注,目前主要的研究热点在于其高效通用的求解模型。ALTINTAS[7]给出了7段式S型加减速模型,但未给出S型加减过程中的求解方法;石川等[8]将S型加减速归纳成8种情况,采用解析式和二分迭代的方法对其进行求解;尹国梁[9]将S型加减速曲线17种不同类型的速度划分为3类,再利用二分法进行求解;朱明等[10]利用拉格朗日法构造二次方程来逼近无理方程求解,但精度却无法保证;杨亮亮等[11]将S型加减速中的五元非线性方程转化成二元非线性方程组和一元线性方程组,再用牛顿迭代法和迭代修正的方式求解。由于S型加减速算法的表达式是分段表达式,上述研究都不能将方程式转化成一个类似于二次方程求根的公式,只能采用二分迭代法、牛顿迭代法以及拟合法等数值解析的方法求解。
综上所述,一种7段式S型加减速控制算法的解析式方法是目前国内数控系统所缺乏的。本文提出了一种7段式S型曲线加减速控制算法及其解析式的求解方法,研究基于给定的轨迹长度与临界长度对比进行分类的方式,将其转换成一元二次方程、一元三次方程或一元四次方程来求解各段运行时间,最后在自主开发的多轴运动控制器上进行验证。
1 7段式S型曲线加减速控制模型
S型曲线加减速的名称由系统在加减速控制阶段的速度曲线形状呈现出S型而得来。如图1所示,正常情况下S曲线加减速的运行过程可分为7段:加加速段、匀加速段、减加速段、匀速段、加减速段、匀减速段、减减速段。
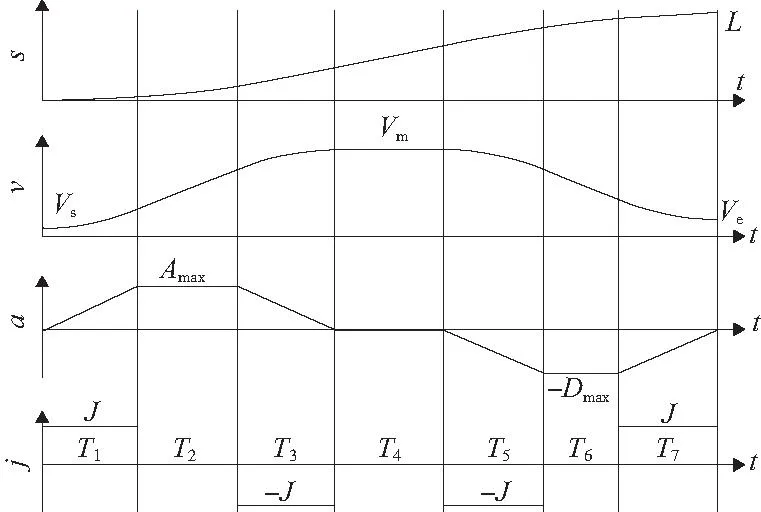
图1 7段S型加减速示意图
图1中:T1表示加加速段的运行时间;T2表示匀加速段的运行时间;T3表示减加速段的运行时间;T4表示匀速段的运行时间;T5表示加减速段的运行时间;T6表示匀减速段的运行时间;T7表示减减速段的运行时间;j表示加加速度曲线;a表示加速度曲线,v表示速度曲线,s表示位移曲线;Vs表示初速度;Ve表示末速度;Vm表示最大驱动速度;L表示实际路径长度。
设电机加速度曲线从0达到最大值和从最大值到0所用的时间相等,此时间定为系统的一个特性时间常数tm,图1中,Amax=Dmax。
在目标运动过程中,A表示最大加速度;J表示最大加加速度。当加速度能够达到最大值时,T1=T3=T5=T7=A/J=tm;当加速度无法达到最大值时,T1=T3,T5=T7。
7段式S型加减速控制模型中加加速度j(t)的计算公式为
(1)
加速度a(t)的计算公式为
(2)
速度v(t)的计算公式为
(3)
位移s(t)的计算公式为
(4)
式中:令k=1,2,…,7;tk表示各个阶段的过渡时刻;τk表示局部时间坐标,即以各个阶段的起始点作为零点的时刻;Tk表示各个阶段的持续运行时间。
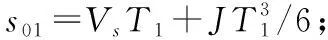
匀速段的运行时间T4的计算公式为
(5)
加速区具体包括加加速段、匀加速段、减加速段,加速区的路径长度Sa的计算公式为
(6)
减速区具体包括加减速段、匀减速段、减减速段,减速区的路径长度Sd的计算公式为
(7)
则加速区的路径长度与减速区的路径长度的总和Sall的计算公式为
Sall=Sa+Sd
(8)
当初速度可达末速度时,则加/减速段长度也可表示为[9]
La(Vs,Ve)=Ld(Ve,Vs)=
(9)
式中:La(Vs,Ve)表示从初速度Vs加速度到末速度Ve的路径长度;Ld(Ve,Vs)表示从末速度Ve减速到初速度Vs的路径长度。
2 S型曲线加减速具体控制算法
2.1 计算临界长度
典型的S型加减速控制算法由7段组成,但由于初速度、末速度、实际路径长度等限制,并不能保证每次速度规划都存在完整的7段。可以将所有的速度规划类型分为3大类:仅存在加(减)速度类型、有匀速段类型和无匀速段类型。由式(10)可求得第一临界长度
L1=La(Vs,Ve)=Ld(Ve,Vs)
(10)
第二临界长度
L2=La(Vs,Vm)+Ld(Vm,Ve)
(11)
式中:La(Vs,Vm)表示从初速度Vs加速至最大驱动速度Vm时的路径长度;Ld(Vm,Ve)表示从最大驱动速度Vm减速至末速度Ve时的路径长度。
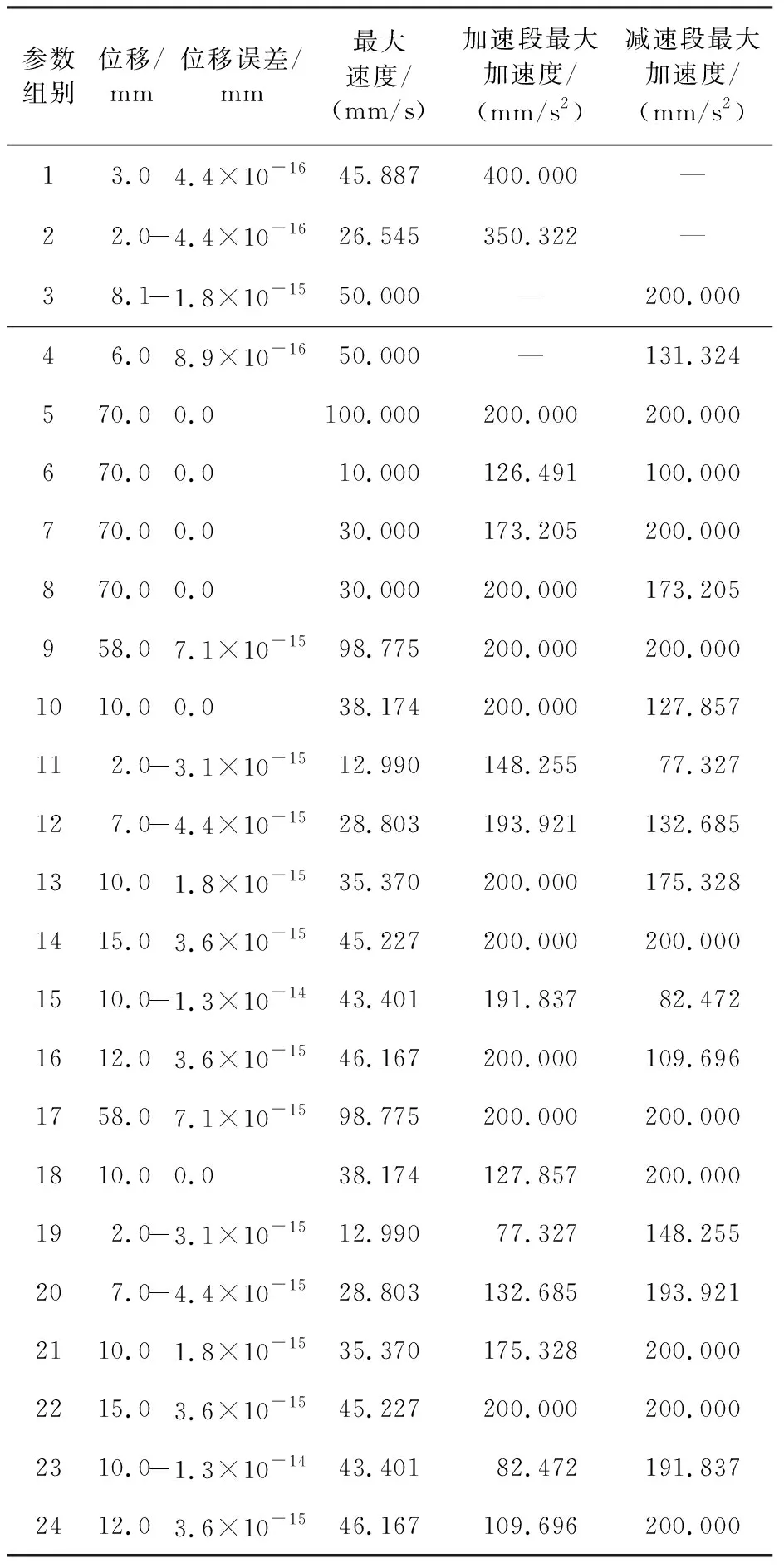
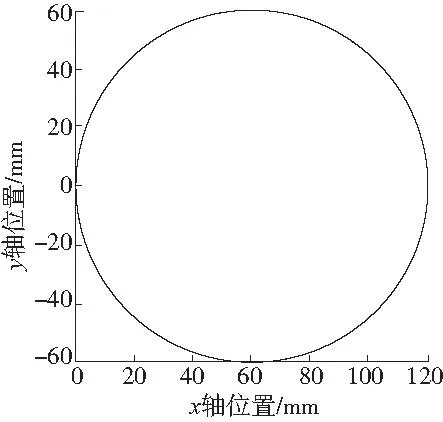
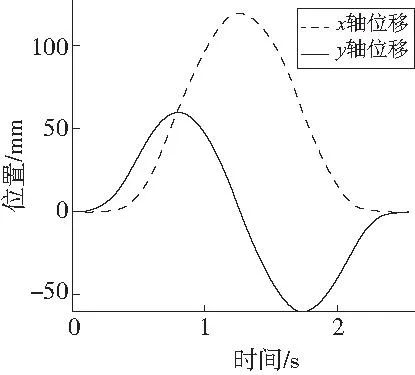
若实际路径L≤L1时,仅存在加(减)速度类型,则说明从初速度Vs不能加(减)速到达末速度Ve;若实际路径L≥L2时,有匀速段类型,则说明从初速度Vs可加速到最大速度Vm,再从最大速度Vm减速到末速度Ve;若L1 当实际路径L≤L1仅存在加(减)速时,判断是否存在匀加速段或匀减速度段可分为4种情况讨论。其中:S13为当T1=T3=A/J,T2=0,T4=T5=T6=T7=0时运动过程的路径长度;S57为当T1=T2=T3=T4=0,T5=T7=A/J,T6=0时运动过程的路径长度。 1)当L≤L1且Vs≤Ve,若(Ve-Vs)>(A2/J)且L>S13时 该段规划从初速度Vs加速到末速度Ve可达到最大加速度,即存在匀加速段,则可确定目标运动过程仅包括加加速度段、匀加速段、减加速段,并得到T1=T3=A/J=tm,T4=T5=T6=T7=0。 根据目标运动过程和式(6)得到第一方程 (12) 最后,利用一元二次方程的求根公式求解第一方程,舍去T2的非可行解即可。 2)当L≤L1且Vs≤Ve,若(Ve-Vs)≤(A2/J)或L≤S13时 该段规划从初速度Vs加速到末速度Ve不能达到最大加速度,即不存在匀加速段,则可确定目标运动过程仅包括加加速度段、减加速段,并得到T2=T4=T5=T6=T7=0。 根据目标运动过程和式(6)得到第二方程 (13) 最后,利用一元三次方程的盛金公式求解第二方程,舍去T1的非可行解即可。 3)当L≤L1且Vs>Ve,若(Vs-Ve)>(A2/J)且L>S57时 该段规划从初速度Vs减速到末速度Ve能达到最大加速度,即存在匀减速段,则可确定目标运动过程仅包括加减速段、匀减速段、减减速段,并得到T1=T2=T3=T4=0,T5=T7=A/J=tm。 根据目标运动过程和式(7)得到第三方程 (14) 最后,利用一元二次方程的求根公式求解第三方程,舍去T5的非可行解即可。 4)当L≤L1且Vs>Ve,若(Vs-Ve)≤(A2/J)或L≤S57时 该段规划从初速度Vs减速到末速度Ve不能达到最大加速度,即不存在匀减速段,则可确定目标运动过程仅包括加减速段、减减速段,并得到T1=T2=T3=T4=T6=0。 根据目标运动过程和式(7)得到第四方程 (15) 最后,利用一元三次方程的盛金公式求解第四方程,舍去T5的非可行解即可。 当实际路径L≥L2有匀速段时,可根据加速段和减速段是否能达到最大加速度来分为4种情况进行讨论。 1)当L≥L2,若(Vm-Vs)>(A2/J)且(Vm-Ve)>(A2/J)时 该段规划的加速段和减速段都可达到最大加速度, 可确定目标运动过程包括加加速段、匀加速段、减加速段、匀速段、加减速段、匀减速段、减减速段,根据目标运动过程得到第五方程 (16) 2)当L≥L2,若(Vm-Vs)≤(A2/J)且(Vm-Ve)≤(A2/J)时 该段规划的加速段和减速段都不能达到最大加速度,则可确定目标运动过程仅包括加加速段、减加速段、匀速段、加减速段、减减速段,根据目标运动过程得到第六方程 (17) 3)当L≥L2,若(Vm-Vs)≤(A2/J)且(Vm-Ve)>(A2/J)时 该段规划的加速段不能达到最大加速度,减速段能达到最大加速度,则可确定目标运动过程仅包括加加速段、减加速段、匀速段、加减速段、匀减速段、减减速段,根据目标运动过程得到第七方程 (18) 4)当L≥L2,若(Vm-Vs)>(A2/J)且(Vm-Ve)≤(A2/J)时 该段规划的加速段能达到最大加速度,减速段不能达到最大加速度,则可确定目标运动过程仅包括加加速段、匀加速段、减加速段、匀速段、加减速段、减减速段,根据目标运动过程得到第八方程 (19) 当L1 1)当L1 该段规划从初速度Vs加速到末速度Ve存在匀加速段,并且实际路径L>S12357以及(Vm-Ve)>(A2/J),说明从新的最大驱动速度V′m减速到末速度Ve可达最大加速度,即存在匀减速段,则可确定目标运动过程仅包括加加速段、匀加速段、减加速段、加减速段、匀减速段、减减速段,可得到 T2=(Ve-Vs)/A+T6,T1=T3=T5=T7=A/J=tm (20) 根据目标运动过程和式(8)得到第九方程 (21) 最后,利用一元二次方程的求根公式求解第九方程,舍去T6的非可行解即可。 2)当L1 该段规划从初速度Vs加速到末速度Ve存在匀加速段,并且实际路径L≤S12357或者(Vm-Ve)≤(A2/J),说明从新的最大驱动速度V′m减速到末速度Ve不能达到最大加速度,即不存在匀减速段,则可确定目标运动过程仅包括加加速段、匀加速段、减加速段、加减速段、减减速段,则可得到 (22) 根据目标运动过程和式(8)得到第十方程 (23) 最后,利用费拉里法求解关于T5的一元四次方程,舍去T5的非可行解即可。 3)当L1 该段规划从初速度Vs加速到新的最大驱动速度V′m, 再减速到末速度Ve都不能达到最大加速度,即不存在匀加速段和匀减速段,则可确定目标运动过程仅包括加加速段、减加速段、加减速段、减减速段,可得到T1=T3,T5=T7,T2=T4=T6。 根据速度曲线公式和式(6)得到 (24) (25) 根据式(24),可得: (26) 将式(26)代入式(25)中,可得 (Vs+Ve)·(T1+T5)+J·T1·T5·(T1+T5)=L (27) 令 (28) 由式(28)及式(24)可得 (29) 将式(29)代入式(27)可得第十一方程 (30) 然后,利用费拉里法求解关于m的一元四次方程得到可行解,最后,根据式(28)和式(26)即可求解T1、T5。 该段规划可确定目标运动过程仅包括加加速段、减加速段、加减速段、减减速段,根据目标运动过程利用第十一方程求解即可。 5)当L1 该段规划可确定目标运动过程仅包括加加速段、匀加速段、减加速段、加减速段、减减速段,根据目标运动过程利用第十方程求解即可。 6)当L1 该段规划可确定目标运动过程仅包括加加速段、匀加速段、减加速段、加减速段、匀减速段、减减速段,根据目标运动过程利用第九方程求解即可。 7)当L1 该段规划可确定目标运动过程仅包括加加速段、减加速段、加减速段、减减速段,根据目标运动过程利用第十一方程求解即可。 8)当L1 该段规划可确定目标运动过程仅包括加加速段、匀加速段、减加速段、加减速段、减减速段,根据目标运动过程利用第十方程求解即可。 基于三轴正交的数控系统实验平台如图2所示。主要包括PC机、ADT8989H1高性能运动控制卡、步进电机以及正交工作台。图2中,ADT8989H1高性能运动控制卡处理器选用某公司XC7Z010-1CLG400I4334, 用于计算各坐标轴所需信息。所研究的7段式S型曲线加减速控制算法均在该处理器中实现,可用于多轴运动控制。将上述总共24种参数不同的情况通过PC机下发到ADT8989H1高性能运动控制卡,经过S型加减速控制处理,采集并分析ADT8989H1高性能运动控制卡实际输出的位移、最大速度和最大加速度以验证提出的S型曲线加减速控制算法的有效性。 图2 三轴正交的数控系统测试平台 S型加减速控制算法实现流程图如图3所示。 图3 S型加减速控制算法实现流程 S型加减速控制算法实现要有3个步骤:1)读取S型曲线加减速控制所需要的运动信息;2)根据加减速类型判断,计算S型曲线加减速7段所对应的时间;3)根据S型曲线加减7段对应时间以及系统参数,实时计算各轴每个周期的输出量,直至整段轨迹加减速控制完成。 设置系统参数:插补周期1ms,24种不同参数的运动轨迹参数如表1所示,对每组轨迹分别进行S型曲线加减速控制。 表1 24种不同参数的S型运动轨迹 表2为采用24种不同参数的S型曲线加减速控制后实际输出的位移、最大速度和最大加速度统计结果。由表2可知,所提出的S型加减速控制算法能正确规划出不同轨迹参数下的速度变化曲线,在加速阶段、匀速阶段以及减速阶段,达到的实际最大速度和最大加速度均小于设定的最大驱动速度和最大加速度,说明所提出的S型曲线加减速算法可保证最大速度及最大加速度不超限。由表2可知,24组实际输出的位移与对应给定的位移误差最大值为第15组和23组的1.3×10-14mm,说明计算输出的实际轨迹长度与给定轨迹长度相等。 表2 24种不同参数的S型曲线实际输出参数 在所搭建的基于三轴正交的数控系统实验平台上,进行单段圆弧加工实验验证。设置系统参数:插补周期为1ms,各轴最大速度为300mm/s,各轴最大加速度为800mm/s2;设置运动轨迹参数:插补起点速度和终点速度为0mm/s,最大插补驱动速度为200mm/s,最大插补加速度为500mm/s2,最大插补加加速度为2 000mm/s3,圆弧轨迹起点终点均为坐标原点,圆弧半径为60mm。圆弧加工输出的位移合成轨迹、两轴位移轨迹、速度、加速度分别如图4—图7所示。 图4 两轴位移曲线合成轨迹 由图4和图5可知,x轴和y轴输出位移曲线相互协调,同时到达各自指定的终点位置,两轴合成的位移曲线为给定的整圆轨迹;由图6和图7可知,两轴的速度曲线平滑过渡,加速度曲线连续,并且两轴速度曲线、加速度曲线以及合成的速度曲线、加速度曲线的最大值都未超过设定的最大值。 图5 两轴位移曲线 图6 速度曲线 图7 加速度曲线 为了解决数控系统中所缺乏的7段式S型加减速控制算法的解析式方法,本文利用给定的路径长度与第一临界长度和第二临界长度进行对比,将所有的S型曲线的加减速控制划分成24种情况,并归纳为11种情况的一元二次、一元三次或一元四次方程求解的形式,再利用求根公式即得到S型7段对应的时间。实验结果表明:所提出的S型曲线加减速控制方法计算时间短、精度更高,能很好地满足加工要求,减少了机床运动的冲击和震动,特别适合高精加工,提高了机床的加工精度和效率。2.2 仅存在加(减)速度类型
2.3 有匀速段类型
2.4 无匀速段类型
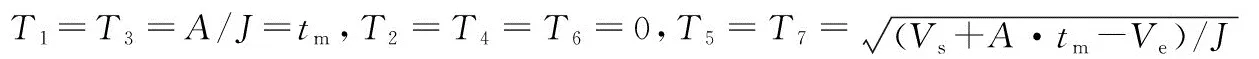
3 S型曲线加减速控制算法实验验证

3.1 S型曲线加减速控制算法实现
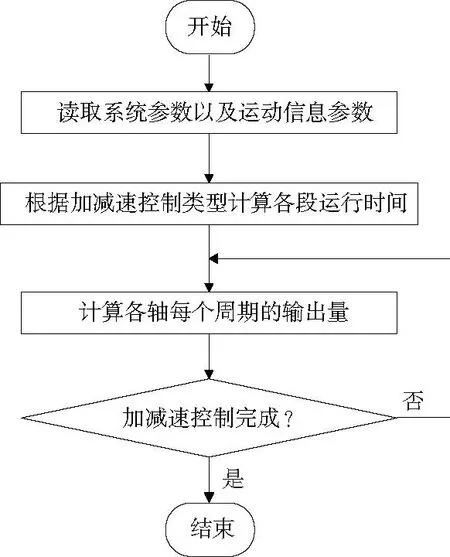
3.2 实验验证与分析

3.3 加工实例


4 结语
