螺栓连接梁非线性振动的定频试验研究

汤涛,臧朝平,张根辈,张磊,陈俊杰

(1. 南京航空航天大学,江苏 南京 210016;2. 中航工业航空动力控制系统研究所,江苏 无锡 214036)

0 引言

螺栓连接具有简单、可靠和装拆方便等优点,在航空、航天、兵器、船舶、电力、机械等工程领域广泛使用。但是螺栓连接结构中存在摩擦、接触、拧紧等大量非线性、不确定性问题,如果设计不当,使用中发生螺栓断裂、松动、连接界面变形等故障,可能会引起严重事故。

在过去的几十年中,国内外学者对螺栓连接结构的动力学建模仿真做了大量的研究。刘宗魁、王攀等[1-2]基于螺栓连接模型的刚度理论、赫兹接触理论和M-B分形模型,推导了不同螺栓预紧力作用下的亚区域薄层单元的弹性模量,使用隔板薄层单元模拟航空发动机匣的螺栓连接结构。王立等[3]采用一种基于参数灵敏度的动力学模型确认方法建立了航空发动机连接机匣。SEGALMAN等[4]用单个非线性本构单元,即Iwan单元,模拟螺栓周围的接触区域耦合的两个刚性表面,该单元可以模拟连接界面的微滑移。FESTJENS等[5]开发了一种准静态技术,后来LACAYO等[6]对其进行了简化,创建了一种高效、准确的算法,用于计算螺栓连接界面中建立的Iwan元件模型的振幅相关频率和阻尼。王东等[7]从螺栓连接结合面的跨尺度物理机理角度出发,建立接触载荷与变形的非线性关系。胡阳等[8]提出了螺栓松动仿真的建模方法,分析了循环往复载荷作用下接触状态与残余预紧力的变化规律,并研究了外部激励变化对螺栓连接松动的影响。

由于螺栓连接结构存在非线性、不确定性因素,还需要开展试验研究,利用试验数据进行螺栓连接模型修正和参数辨识。张根辈等[9]对一个螺栓连接的三层框架结构建立了3类不同类型单元的动力学模型,通过模态计算与测试结果的比较分析,讨论了连接建模中的不确定因素。郭宁等[10]采用一种结合薄层单元法和模型修正的建模方法,建立了螺栓连接板结构模型,通过试验数据验证了该方法的有效性。但目前主要的试验方法仅局限于线性条件,螺栓连接界面的非线性试验测量仍然非常困难[11]。

2015年,为了深入研究螺栓连接结构接触界面的试验测量与建模仿真方法,同时考虑到试验的可重复性,BRAKE等[12]设计了Brake-Reuß螺栓连接梁。该梁在低预载水平下会表现出显著的强非线性,而在高预载水平下表现出接近线性的行为,可以作为螺栓连接的标准结构进行研究。BONNEY、BALAJI、LACAYO等[13-15]采用不同的非线性建模方法,对Brake-Reuß螺栓连接梁进行了大量的仿真计算分析。但是,目前对于Brake-Reuß螺栓连接梁的非线性动力学特性仍然缺乏系统、精确的试验研究。

2019年,ZHANG等[16-18]提出了一种定频试验方法,测量了非线性转子及其支承结构在每个频率下激励与响应之间的关系。本文将定频试验方法应用到国际标准的Brake-Reuß螺栓连接梁结构,改进了螺栓连接结构的定频试验方法,对螺栓连接梁结构的非线性振动特性进行深入研究,精确测量结构在每个频率下激励与响应之间的非线性关系。并基于定频试验结果,重构恒力条件下的非线性幅频及相频特性曲线,分析不同激励水平及不同拧紧力矩条件下结构非线性振动响应的变化规律。

1 螺栓连接梁的定频试验方法

1.1 螺栓连接梁的结构介绍

螺栓连接梁如图1所示,由2根尺寸相同的梁,通过3颗螺栓连接组成,组装后的连接梁长度为820mm。每根梁截面尺寸为30mm×30mm,一端有1个半厚度延伸,材料为304不锈钢。螺栓的规格为M6×50,材料也是304不锈钢。这种保证螺栓连接梁的整体长度相对螺栓搭接界面长度较长,在外界的横向激励下更容易产生摩擦行为。其中在两根梁的轴向连接界面保留1mm间隙,可以避免2个轴向接触面发生摩擦,从而聚焦螺栓搭接面摩擦接触引起的非线性振动。

1.2 螺栓连接梁的试验装置

螺栓连接梁的试验装置如图2所示。连接梁保持水平状态,采用弹性绳悬挂,模拟自由—自由边界条件。采用电动激振器(型号为美国某公司的ET-160电动激振器)进行激励,激振器底座安装在铸铁平台上。激振器的顶杆与连接梁水平对齐,顶杆与结构之间安装阻抗头以测量实际激振力。采用激光测振仪(型号为PSV-400)测量连接位置的振动响应。激光测振仪采用非接触测量方式,测量精度高,无附加质量影响。在计算机上的信号发生器中设置正弦信号的电压和频率,通过功率放大器放大,驱动激振器产生正弦激励,以最大限度激发结构非线性。

图2 螺栓连接梁的试验装置

1.3 螺栓连接梁的定频试验方法

本文改进了定频试验方法,在定频试验的基础上重构了恒力条件下的频率响应曲线并应用于螺栓连接结构的非线性振动测试。这种方法利用电动激振器频率精确的特点,无需采用反馈控制,简便易行。试验流程如图3所示。

图3 螺栓连接梁的定频试验流程

螺栓连接梁的定频试验流程主要包括3部分。

1)对螺栓连接梁进行不同条件下的快速正弦扫频,检测系统的非线性,观察非线性的影响范围,确定合适的频率范围和激励电压。

2)在关注的频率范围内,确定合适的频率间隔,对每个频率进行定频测试。在每个频率下固定激励频率,不断增大激励电压,精确测量每个频率ω下响应幅值R、响应与激励之间相位差φ随激励幅值F变化的曲线。其中对于激励信号、响应信号采用正周期重采样,通过频谱分析精确提取基频及倍频成分,详见文献[17]。

(1)

3)利用定频试验结果,重构恒力条件下的频率响应曲线包括幅频曲线和相频曲线。例如,给定激励水平为F0,则每个频率ωk下的响应幅值Rk和相位差φk分别为:

Rk=g(F0,ωk)

(2)

φk=h(F0,ωk)

(3)

2 螺栓连接梁的非线性振动试验

2.1 快速正弦扫频

在3种不同拧紧力矩条件分别为1N·m、2N·m、3N·m下,对螺栓连接梁进行同等水平的快速正弦扫频,以初步观察螺栓连接非线性对结构频率响应的影响情况。试验中,在试验件上沿长度方向分两行均匀布置30个测点,利用扫描式激光测振仪测量。

不同拧紧力矩下测量得到的频响曲线如图4所示。从图4(a)中可以看出,非线性主要影响共振附近的响应,特别是第1阶弯曲模态(振型如图5所示),对第2阶弯曲模态(振型如图6所示)影响不大。随着螺栓拧紧力矩的增大,第1阶模态最大响应对应的峰值频率逐渐增大,如图4(b)所示,分别为 110.6Hz、113.1Hz和115.3Hz,反映了结构连接刚度增大的趋势。

图4 不同拧紧力矩下螺栓连接梁的频率响应曲线

图5 第1阶模态振型

图6 第2阶模态振型

2.2 定频试验

针对受非线性影响显著的第1阶模态,在3种不同的拧紧力矩下,对螺栓连接梁开展定频试验。

在定频试验中,激励信号为单频正弦。激励频率范围覆盖第1阶模态的共振区,在拧紧力矩为1N·m时,激励频率范围为108Hz～112Hz;在2N·m时,激励频率范围为111Hz～115Hz;在3N·m 时,激励频率范围为112Hz～115Hz。频率步长均为0.1Hz。每个频率下电动激振器的输入电压范围为0.05V～2.00V,步长为0.05V,即对每个频率进行40次测试。每次测试中,采样频率为10 000Hz,采样时间为20s,保证每次测试中响应达到稳定状态。

在3N·m 拧紧力矩下,定频试验测量得到的不同频率下速度响应的幅值、相位差随着激励幅值的变化曲线如图7和图8所示。可以看出,在不同激励频率下,随着输入电压的增大,响应及相位差随着激励幅值发生了复杂的变化:对于远离共振的频率,例如112Hz,响应幅值随激励幅值基本线性变化,相位基本保持稳定不变,说明该频率下响应受非线性影响不大;但是对于靠近共振附近的频率,例如114Hz,响应幅值随激励幅值发生复杂的“S”型变化,相位变化则超过90°,反映了螺栓连接非线性对结构响应的复杂影响。

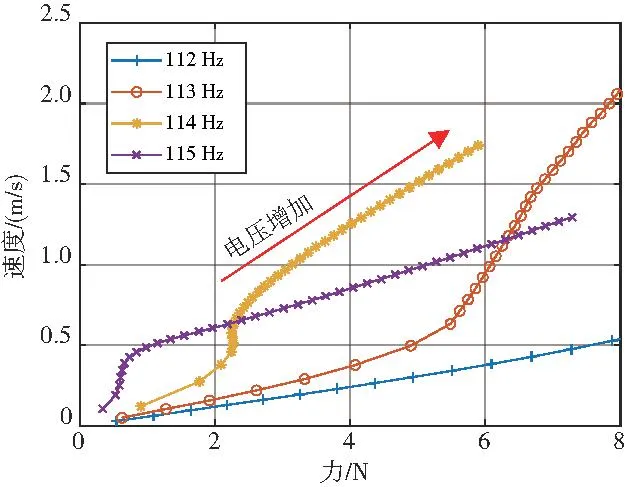
图7 不同频率下激励与响应之间的幅值曲线

图8 不同频率下激励与响应之间的相位差

3 螺栓连接梁的恒力响应构建

将定频试验数据重构,获取不同激励水平下的频率响应曲线,可以深入分析螺栓连接对结构非线性响应的影响。下面主要以3N·m拧紧力矩为例,分析不同激励水平对结构非线性响应的影响;以3N的恒力激励为例,分析不同拧紧力矩对结构非线性响应的影响。

在3N·m 拧紧力矩下,重构的不同激励水平下结构频率响应的幅频特性曲线和相频特性曲线如图9所示。从图中可以看出,随着激励水平的增大,第1阶模态最大响应对应的峰值频率降低,结构呈现刚度软化现象。其他拧紧力矩下情形类似。

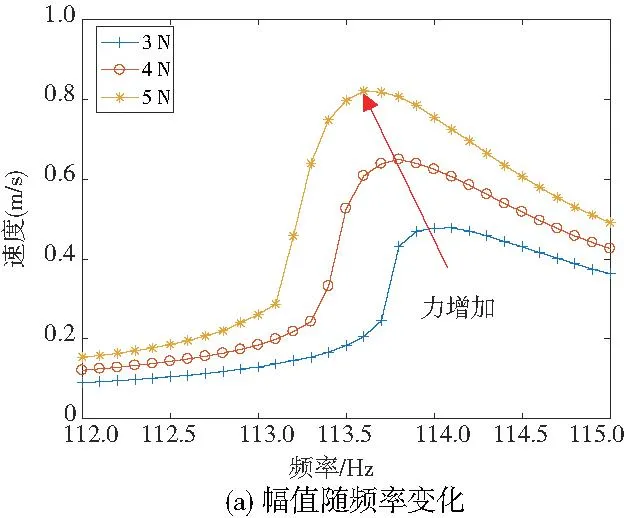
图9 螺栓拧紧力矩为3N·m 时的恒力频率响应

在同一激励水平3N的恒力条件下,不同拧紧力矩下的频率响应如图10所示。从图中可以看出,随着螺栓拧紧力矩的增加,连接梁的共振频率逐渐增加,整体的刚度增强。其他激励水平下情形类似。

图10 外激励为3N时不同螺栓拧紧力矩下的频率响应

4 结语

本文改进了螺栓连接结构的定频试验方法,对国际上标准的Brake-Reuß螺栓连接梁结构的非线性振动特性进行了深入研究,主要得到以下结论。

1)该试验方法可以精确测量螺栓连接结构在不同频率下响应与激励之间的幅值和相位关系。

2)利用定频试验测量结果,可以重构恒力条件下频率响应的幅频特性曲线和相频特性曲线。

3)在同一拧紧力矩下,随着外激励水平增大,螺栓连接梁的峰值频率逐渐减小,呈现刚度软化现象;在同一外激励水平下,随着螺栓拧紧力矩增大,连接梁的峰值频率逐渐增加,整体连接刚度增强。

上述定频试验方法无需反馈控制,简便易行,可以为结构的非线性建模仿真提供精确的参考数据,有助于深入认识结构的非线性振动特性。