基于旋量理论的并联机构过约束分析步骤的改进

汪建晓

（佛山科学技术学院机电工程学院，广东佛山528225）

并联机构是由基座、动平台以及联接它们的若干分支所组成的多闭环机构，具有刚度大、精度高以及动态响应快等特点，因而在运动模拟、取放作业、组装以及多轴加工等许多场合得到广泛应用。

在进行并联机构的分析与综合时计算其自由度是最基本内容之一。当采用传统的机构自由度计算公式即Grübler-Kutzbach（G-K）公式对并联机构进行分析时，常会由于机构的特殊几何形状而不能得到正确解，特别是对于一类所谓过约束并联机构。其原因在于G-K公式将所有约束都当成有效约束，即使那些不影响机构自由度的冗余约束（或虚约束）也不例外。

旋量是具有旋距要素的线矢量（也称为螺旋）。旋量可以表示运动学中的一般刚体运动或者静力学中的广义力（包括力和力偶）。旋量理论可以追溯到18世纪的Mozzi瞬时运动轴及19世纪初叶的Poinsot合力中心轴与Chasles位移轴。至1876年，Ball完成了对这一理论的系统研究，并体现在其1900年的著作当中。

并联机构的运动和约束情况较为复杂，因而最适宜采用旋量理论进行描述。20世纪80年代以来陆续有学者开始用旋量来表达Stewart平台和6-6R并联机构等的分支运动，用旋量理论研究少自由度并联机构的型综合，以及用互易旋量研究一些并联机构自由度的计算方法。

戴建生、黄真等人［1-2］系统研究了并联机构的一系列旋量系，创建了并联机构旋量系分析的理论体系，揭示了这些旋量系与机构运动和约束之间的内在联系，并提出了一种修正的G-K公式，为并联机构的自由度和过约束分析计算奠定了理论基础，引起国际上机构学界的广泛关注［3-5］。近十余年来这一理论体系得到丰富和完善［6］，已逐步普及到相关专业研究生或高年级本科生教材中去了［7-8］。

文献［1-2］重点研究了各旋量系之间的关系，并用多个示例验证了修正的机构自由度计算方法的正确性，然而并未给出条理化的机构自由度与过约束（包含虚约束和公共约束）分析的步骤，这对于初学者掌握这一方法有些不便。文献［7-8］给出的机构自由度与过约束分析步骤除部分变量符号不同外，步骤的内容都是一致的，然而当笔者按这些步骤进行并联机构自由度计算时，却发现过约束的分析步骤中存在公式表达不准确、不完善的问题。

本文的目的在于针对上述问题，提出一种改进的机构过约束分析的步骤，以便于基于旋量理论的并联机构自由度计算方法的推广应用。

1 机构自由度计算的G-K公式及其修正

自1869年Chebychev提出第一个机构自由度计算公式至今的150年里，很多学者一直在找寻通用的机构自由度计算公式，提出的公式在40种以上［3，9］。其中，较为传统的、最具代表性的、应用也最为普遍的要属Grübler-Kutzbach公式［10-11］，即

其中，F为机构的自由度数；d为机构的阶数，d=6-λ，λ为公共约束数；n为构件数（包含机架）；g为运动副数；fi为第i个运动副的自由度数目。

不过，目前已证明，对于很多机构的自由度，利用该公式计算的结果都不正确，因此提出了许多修正公式。戴建生、黄真等人提出的修正的G-K公式为［1-2，6］

其中，ν为机构的冗余约束（或虚约束）数。

当考虑机构的局部自由度时，式（2）进一步修改为［12］

其中，ζ为机构的局部自由度数。

应用式（2）或（3）计算机构自由度的难点在于公共约束和虚约束的判定，而基于旋量理论的并联机构过约束分析方法能有效地解决这个难题。

2 基于旋量理论的并联机构自由度和过约束分析方法

如图1所示，并联机构中包含3个基本互易旋量系对，分别是：1）与单个从基座到动平台的分支（ii=1，2，…，p，其中p为分支数）对应的分支运动旋量系Sbi和分支约束旋量系。2）与动平台对应的平台运动旋量系Sf和平台约束旋量系Sr。3）与整个机构对应的机构运动旋量系Sm和机构约束旋量系Sc。此外，还有分支补约束旋量系和平台补约束旋量系等。

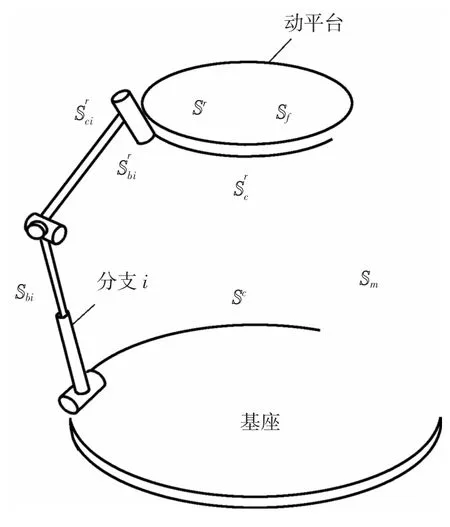
图1 并联机构中的几对基本旋量系

假定每个分支的旋量是线性独立的，则冗余自由度和奇异在每个分支中都被排除。这些旋量系的定义与相互关系详见文献［1-2，6-7］。为叙述方便，下文主要以文献［6-7］为代表进行阐述。

这里先给出基于旋量理论的通用自由度分析过程［7］，这也是机构过约束分析的前序步骤，具体步骤如下。

（1）判断机构是否含有局部自由度，并计算出具体数值ζ。

（2）构造各个分支的运动旋量系Sbi。

（5）根据SfΔSr=0，计算得到动平台的运动旋量系Sf。

（6）观察Sf的特点，进一步确定机构的自由度分布情况。

（7）改变机构的位形，重复上述步骤，以验证所求得的自由度是否为全周自由度。如果前后自由度性质不变，则为全周自由度；否则为瞬时自由度。

需要指出的是，在文献［7］中旋量系和旋量系的矩阵表示采用相同的符号，例如分支运动旋量系和分支约束旋量系分别用Sbi和表示，而上述步骤3的矩阵方程为，这容易造成混淆。本文对其进行了区分，旋量系与旋量集的符号均用空心体表示，而旋量系的矩阵用对应字母的黑斜体表示。在上述矩阵方程中，为进行旋量系互易运算的矩阵，由3×3分块矩阵组成，E为单位矩阵。运，n为运动旋量系的阶数，各旋量均采用列阵表达。

本文着重讨论机构过约束的分析。文献［6］在论述各旋量系的定义与相关定理的基础上，给出了机构公共约束数λ和虚约束数ν的计算公式，分别为动旋量系的矩阵为，约束旋量系的矩阵为

其中，dim（）表示旋量系的阶数，card（〈〉）表示旋量系多重集（旋量集）中元素的个数。

文献［7］给出的对机构进行过约束（包括公共约束和冗余约束）分析的步骤如下。

集合中的元素个数记作card（〈Sr〉）。

（2）根据Sm＝Sb1∪Sb2∪…∪Sbp，求取整个机构的运动旋量系Sm。

（3）根据SmΔSc=0，求取整个机构的约束旋量系Sc。

（4）根据λ=dim（Sc），确定机构的公共约束数λ。

（5）根据d=6-λ，确定机构的阶数d。

3 过约束分析步骤存在的问题及改进

由上述可知，文献［7］给出的机构自由度和过约束分析的步骤较为清晰，容易实施，特别对于那些初学者来说就有了一个求解过程的指南。但是当利用该步骤进行机构过约束分析时，不难发现它存在以下两个问题。

（1）其步骤1求出的card（〈Sr〉）闲置，没有用于其他计算或分析。

对于第2个问题，文献［6］给出以下关系式

显然，根据这个条件去分解旋量集，重复元素只能存在于一个旋量集中，因而求解具有确定性。

对于第1个问题的解决就稍显复杂。经研究，发现在文献［6］中定义了表征机构公共约束数λ和虚约束数ν总体大小的一个参数，称为综合约束冗余因子。综合约束冗余因子c的计算公式为

综合约束冗余因子c也可以由card（〈Sr〉）与dim（Sr）表示为

由于前序步骤4已求出Sr，即dim（Sr）确定，因此可以用式（8）把上述步骤1求出的card（〈Sr〉）与dim（Sr）相减，求得综合约束冗余因子c，再与式（7）求出的同一参数进行比较，若两者相同，则验证了过约束分析的正确性。

针对这两个问题进行改进后，对机构进行过约束（包括公共约束和冗余约束）分析的步骤如下。

（2）根据Sm=Sb1∪Sb2∪…∪Sbp，求取整个机构的运动旋量系Sm。

（3）根据SmΔSc=0，求取整个机构的约束旋量系Sc。

（4）根据λ=dim（Sc），确定机构的公共约束数λ。

（5）根据d=6-λ，确定机构的阶数d。

（9）计算综合约束冗余因子c=（p-1）λ+ν，若与前面求出的c一致，则表示过约束分析正确。

与改进前的过约束分析步骤相比，可知改进后步骤1与7有修改，且增加了一个新的步骤9。

4 算例

为了便于对照，这里分别从文献［1］和［7］中找出其有代表性的1个算例，并对改进后的机构过约束分析步骤加以验证。

例1分析图2所示Sarrus机构［7］的自由度和过约束。图2中每个分支中转动副（R）的轴线相互平行，但两个分支的运动副轴线相互垂直。

解该机构可看成是由2个分支组成的单环机构，机构自由度分析的步骤如下。

（1）判断可知机构无局部自由度，即ζ=0。

（2）建立如图2所示的坐标系，各分支的运动旋量系Sbi为

图2 Sarrus机构及其运动旋量

（6）通过分析Sf的特点，很容易判断出来该机构的自由度为单自由度平动。

（7）由于机构位形改变后，各分支运动副间的几何关系未发生变化，因此计算结果仍然有效。由此可以判断该机构所具有的移动自由度为全周自由度。

通过以下步骤还可进一步对该机构进行过约束（包括公共约束和冗余约束）分析。

（1）求取动平台的约束旋量集〈Sr〉，确定机构的综合约束冗余因子c，分别为

（2）根据Sm=Sb1∪Sb2，求取整个机构的运动旋量系Sm，有

由此可知，计算结果与前面分析得到的自由度一致，表明分析正确。

例2用旋量理论分析图3所示3-RRRH并联机构［1］的自由度和过约束。图3中每一分支均由3个转动副（R）和一个螺旋副（H）组成，而且它们的运动副轴线相互平行。在基座上3个转动副轴线位于同一平面，且对称布置。

图3 3-RRRH并联机构及其运动旋量

解该机构可看成是由3个分支组成的多环机构，机构自由度分析的步骤如下。

（1）判断可知机构无局部自由度，即ζ=0。

（2）建立如图3所示的坐标系，确定各分支及运动副旋量的符号。各分支的运动旋量系Sbi为

（6）通过分析Sf的特点，很容易判断出来该机构的自由度为沿3个坐标轴的移动。

（7）由于机构位形改变后，各分支运动副间的几何关系未发生变化，因此计算结果仍然有效。由此可以判断该机构所具有的移动自由度为全周自由度。

通过以下步骤还可进一步对该机构进行过约束（包括公共约束和冗余约束）分析。

（1）求取动平台的约束旋量集〈Sr〉，确定机构的综合约束冗余因子c，即

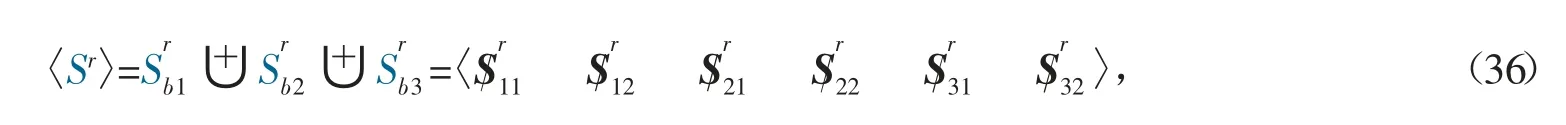
由此可知，计算结果与前面分析得到的自由度一致，表明分析正确。

从例2过约束分析的步骤7还可以得出机构的约束旋量集为

5 小结

本文指出基于旋量理论的机构过约束分析方法或步骤存在的问题，根据权威文献的理论公式，给出了改进后的分析步骤，并以算例加以验证。结果表明，改进后的分析步骤逻辑清晰，公式严谨，便于数据相互验证，使机构过约束分析的方法得到进一步完善，有利于基于旋量理论的机构自由度和过约束分析方法的推广应用。