一种减小柔性冲击的NURBS曲线速度规划算法

冯胜利,赵东标

(南京航空航天大学 机电学院,江苏 南京 210016)

0 引言

常见的速度规划模型有S型、多项式型、三角函数型、指数型等。从S型加减速模型的速度表达式看,它本质上也是一种多项式型加减速模型。三角函数型虽然平滑且无限可微,但是求导积分过程复杂;指数型平滑性较好,但是加减速的起点和终点存在速度突变,且计算也较复杂。因此,对S型和多项式型研究更为深入[1-9]。

传统7段S型加减速模型加加速度一直保持最大值,因此加工效率高。但其加加速度存在突变,产生较大惯性力,因此会对机床产生较大的柔性冲击。本文设计一种速度表达式是四次多项式的加减速模型,其柔性冲击较小,但加工效率偏低。通过引入系数k将其与传统7段S型加减速模型组合产生一种兼顾柔性冲击和加工效率的加减速模型,系数k可以调整S型和四次多项式型加工过程中所占比列,以达到协调柔性冲击和加工效率的目的。

1 速度规划预处理

1.1 自适应速度规划

为保证加工质量,NURBS曲线上任一点的速度应该满足最大弓高误差emax、最大进给速度Vmax、最大法向加速度ANmax、最大加加速度Jmax的约束,并将此速度作为后续速度规划的上限[10-11]。

(1)

1.2 基于速度敏感点的NURBS曲线分段

由式(1)知,曲率极大值点的速度应减小。速度敏感点是曲率极大值点,但并不是所有的曲率极大值点都是速度敏感点,只有满足式(2)的曲率极大值点才称为速度敏感点[12]。以速度敏感点为界将NURBS曲线分段进行速度规划[13],其中曲率k(ui)与曲率半径ρi成反比。

(2)

2 S加减速模型的改进与速度规划

2.1 四次多项式型加减速模型设计

首先,设计一种四次多项式型加减速模型,如图1所示。

图1 四次多项式型加减速模型

该加减速模型的加加速度二阶可导,因此可以极大地减小柔性冲击。

下面给出该模型加减速公式的推导。

以加速段为例,减速段可视为反向加速。加加速度曲线是关于时间的二次抛物线函数,在加速段加加速度的积分为0。

为简化表达式,令t0=0,Ti1=ti1-ti-1。根据amax可知:T11=T12=T31=T32=3amax/4Jmax。进一步可得到以下加加速度方程:

(3)

为了避免重复,加速度和速度方程在后面与传统7段S型结合时一起给出。

2.2 四次多项式模型与S型模型结合

只要加加速度达到最值后能以该值持续一段时间,则可以提高上述四次多项式模型的加工效率。因此本文在四次模型的基础上融入7段S型模型,得到一种兼顾柔性冲击和加工效率的新速度模型,如图2所示。

图2 多项式型和S型组合加减速模型

令ki=Ti1/Ti,Ti1=ti1-ti-1,Ti=Ti1+Ti2+Ti3,其中ki∈[0,0.5]。加加速度曲线在原来二次抛物线的基础上增加了最值的水平线,其余保持不变。因此,T12=T32,T11=T13=T31=T33。由对称性可得,k1=k3,k5=k7。为了减少计算量,假设k1=k3=k5=k7=k。根据ki可将Ti1、Ti2、Ti3合并为一个Ti来处理,图2中细分的15段就可以转化为7段来处理。以加速段为例,减速段可视为反向加速。为简化表达式,令t0=0,加加速度方程如式(4)所示。对加加速度方程积分并代入边界条件可得加速度方程,同理可由加速度方程推出速度方程。加速度和速度方程每段时间分组同加加速度方程,为了避免冗余,式(5)和式(6)每段方程的时间取值范围省略。

(4)

(5)

(6)

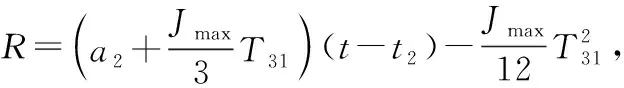
表1 加速度方程中的未知量

表2 速度方程中的未知量

(7)

(8)

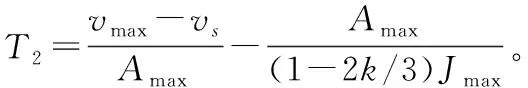
(9)

(10)

同理将vs替换为ve,T2替换为T5,T1替换为T4可以得到减速段的速度变化ΔV-和位移变化ΔS-。

2.3 速度规划

基于预处理的结果,NURBS曲线被速度敏感点分成许多曲线段。每一小段曲线的加减速类型分为如下4种:纯加速、纯减速、加速减速、加速匀速减速。

1)加减速状态判断:根据加减速的位移变化,求得每段曲线加减速状态的判断依据如表3所示。由于本文提出的组合模型考虑了匀加速段和匀减速段,所以需要先用上文的判断式进行判断。为书写简便,表3用ΔS+代表加速段位移,用ΔS-代表减速段位移。

表3 4种加减速状态类型的判断依据

2)速度修正:根据曲线段不同加减速状态类型对速度进行修正。

a)纯加速型或纯减速型:若为纯加速型,需要修正ve;若为纯减速型,需要修正vs。

以纯加速为例,利用vs和L可以反求ve,分为以下两种情况:

①存在匀加速时,将位移公式化简为:

(11)

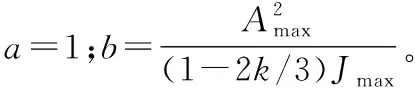
可得修正的ve:

(12)

②不存在匀加速时,将位移公式化简为

(13)

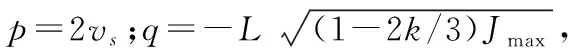
根据Cardan公式[14]可得

(14)

由于速度不能突变,修正了本段的ve需更改下一段曲线的vs。同理,纯减速修正本段的vs需更改上一段曲线的ve。上一段的ve被修改了,所以还要回溯到上一段曲线重新规划。

b)加速减速型:由于加速减速距离受到曲线段长度的限制,最大速度达不到自适应预处理的vmax。修正的v′max在[max{vs,ve},vmax]内通过二分迭代进行求解。

c)加速匀速减速型:因为存在匀速段,所以可以达到自适应速度规划中的最大速度vmax,匀速段时间为

(15)

总体速度规划流程图如图3所示。

图3 速度规划流程图

2.4 k的取值依据与作用

k值的数学意义是四次多项式模型在组合模型中所占的比列。k值越大,速度和加速度曲线越平滑,加工效率越低;k值越小,速度和加速度曲线波动越大,加工效率越高。当k=0,组合模型就是传统的7段式S型;当k=0.5,组合模型就是四次多项式模型。经反复试验,k不能取值过小。因为k过小,会导致组合模型中的加加速度曲线从0加到Jmax的时间过小,二次抛物线部分接近竖直线,斜率过大,对减少柔性冲击的效果不显著。所以考虑运动的平滑性,建议k值不小于0.3。

k起到比例控制作用,让四次多项式部分与传统S型部分始终共存,保证了加加速度的连续性,减少了柔性冲击,而且加加速度能够达到最大值并持续一段时间,保证了加工的效率。此外,系数k的引入增加了进给速度控制的灵活性。

2.5 仿真与实验

为了验证上述NURBS曲线加减速算法的有效性,选取图4中一个二维三叉戟型NURBS曲线进行仿真,其曲率曲线如图5所示。该NURBS曲线参数如表4所示。其中插补周期为1ms,最大速度240mm/s,最大法向加速度4 900mm/s2,最大加加速度48 000mm/s3,最大弓高误差0.001mm,最大速度波动率0.001。

表4 三叉戟NURBS曲线参数

图4 三叉戟型NURBS曲线

图5 三叉戟型NURBS曲线曲率

对该曲线进行仿真加工得到参数k与加工时间t的关系如图6所示。从图6可看出,系数k越大加工时间越长,但是柔性冲击减小。因此本文取k=0.3这个中间值得到的模型和传统7段S型模型进行仿真比较,结果如图7所示。

图6 加工时间t与系数k关系

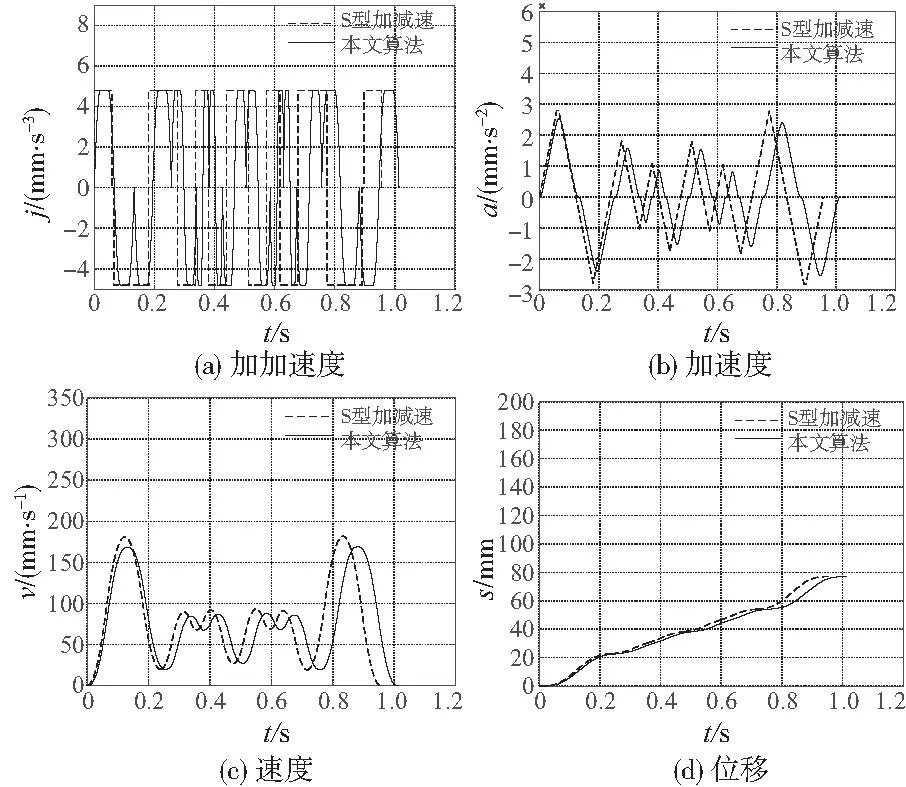
图7 三叉戟型曲线仿真结果

从仿真图对比可以明显看出,相比总以最大加加速度值进行加减速且柔性冲击大的S型加减速,本文加减速算法实现了加加速度连续且平滑,加速度曲线更加平滑,在满足最大加加速度、加速度、进给速度等限制的同时,本文算法加速度最大值更小,柔性冲击更小。从时间上看,7段S型加减速用时0.956 3s,本文算法在k=0.3时用时1.013 6s,相比7段S型加减速增加了5.99%的时间,属于可以接受的以少量加工时间换取更好的加工柔性。

除了加工效率,加工精度也是评价速度规划算法好坏的重要指标。由于实际NURBS曲线插补时是以微小直线段代替曲线,所以存在弓高误差。此外,由于速度规划的速度只能作为理想的速度进行插补点参数预估,使得理想步长与实际步长存在偏差,用速度波动率来表示。因此本文采用文献[15]里的插补算法,对速度波动和弓高误差这两个精度指标进行插补实验比较。此外统计本文速度规划算法和传统7段S型速度规划算法单次插补计算时间。

通常在加工曲线的拐角处,电机会换向,引起柔性冲击,造成拐角附近的加工误差偏大,也会引起实际步长与理想步长相差较大,即速度波动率变大。由图8可知,本文算法的弓高误差与传统7段S型算法变化趋势相似但处处小于传统7段S型算法,特别是在曲线曲率极大值点附近减小了弓高误差。由图9可知,S型算法的速度波动率在曲线曲率极大值点附近超过了上限值0.001,本文算法速度波动率的幅值明显小于传统7段S型算法,且波动次数减少,幅值也没有超出速度波动率的上限值。由图10可知,两种速度规划算法单次插补计算时间都没有超过插补周期1ms,满足插补实时性要求。由于都是采用文献[15]里的插补算法,所以插补计算效率上相差不大。

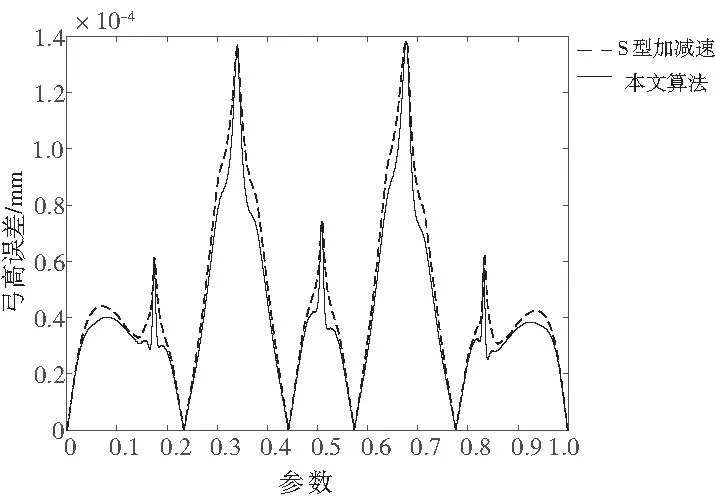
图8 弓高误差图

图9 速度波动率

图10 插补算法计算时间

将相关参数进行统计处理得表5,通过对比可知本文算法在加工精度上要明显优于传统7段S型算法。

表5 弓高误差和速度波动率统计表

总体上看,本文速度规划算法能在加工中全程保持加加速度连续且平滑。相比于传统7段S型加减速,本文速度规划算法速度波动更小,减少了柔性冲击,提高了加工精度。

3 结语

本文为解决传统7段S型柔性冲击大的问题,设计了一种加加速度曲线为二次抛物线形式的四次多项式型加减速模型。为了兼顾加工效率,将四次多项式型加减速模型与传统7段S型加减速模型组合,并引入系数k来调整两种模型的占比,达到加工效率与柔性冲击兼顾的目的,提高了进给速度控制的灵活性,并通过仿真验证了本文算法相比于S型算法能够有效地减少速度波动,减少机床运行时的柔性冲击,提高加工精度,也满足插补实时性要求。