基于AMESim的车辆悬架减震系统优化与仿真

王小龙

(西安工商学院,陕西 西安 710200)

0 引言

车辆悬架作为支撑车辆并进行正常工作的重要结构,其减震系统是车辆能够平稳运行的重要基础,而传统的被动悬架系统因其响应效果差、响应速度慢,己无法满足使用者的要求[1-2]。因此,如何在保证车辆悬架减震系统原有性能的同时,提高车辆悬架减震系统的稳定性及可靠性,成为值得研究的问题。本文设计了一种提高车辆悬架减震系统运行稳定性与可靠性的自动控制系统。通过PID反馈环节对车辆悬架减震系统中的磁流变阻尼器进行有效控制,提高车辆悬架减震系统在载荷不断变化等特殊条件下的可靠性和车辆悬架减震系统的使用范围与效率。

设计目标:

1)进行车辆悬架减震系统模型的建模;

2)进行单神经网络PID算法的优化;

3)进行车辆悬架减震系统PID控制环节仿真实验。

1 车辆悬架的结构与参数

1.1 基本结构

本文选取福特汽车的悬架系统,其车辆悬架减震系统的基本结构[3]如图1所示。

图1 车辆悬架的结构

1.2 基本参数

本文选取福特汽车的某些参数作为本文数据[4],其基本参数如表1所示。

表1 车辆悬架减震系统的基本参数

2 车辆悬架的数学模型与受力分析

2.1 数学模型

本文以半主动悬架为研究对象,其模型如图2所示。将悬架系统简化为刚度元件、阻尼元件,并假设车辆其他部分为质量均匀的质点,且在车辆行进过程中各部分均只产生垂直方向的振动[5-6]。

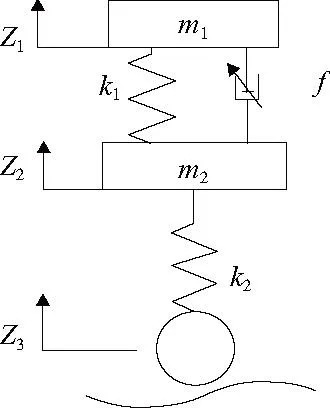
图2 车辆悬架的数学模型

图2中:Z1为簧载质量位移;Z2为非簧载质量位移;Z3为路面激励位移;f为提供的阻尼力。由牛顿第二运动定律与力平衡关系可得出,1/4车悬架的运动方程如下:

(1)

(2)

为了便于研究,本文进行了如下假设:1)车轮刚度不发生变化,车轮刚度系数为常量;2)道路为理想道路,其激励位移近似为0;3)因非簧载质量远小于簧载质量,可忽略不计。

则车辆悬架的数学模型可简化为

m1C1k1(Z1-Z2)=f

(3)

由式(3)可知,减震系统阻尼力受簧载质量、悬架弹簧刚度、悬架阻尼系数和位移增量的影响。

2.2 受力分析

结合图1、图2中车辆悬架减震系统的基本结构,利用AMESim绘制了1/4悬架的仿真模型。如图3所示。

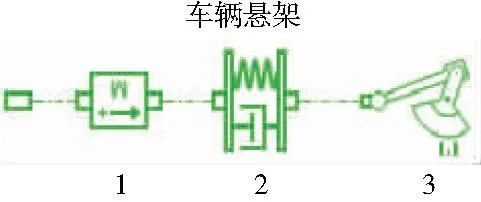
1—簧载质量;2—阻尼系统;3—悬架摆动轴。图3 1/4悬架的仿真模型

本文在AMESim仿真环境中,以图3为基础进行了仿真实验,得到了不同外部负载作用下车辆悬架减震系统的位移相对变化量,如表2所示。

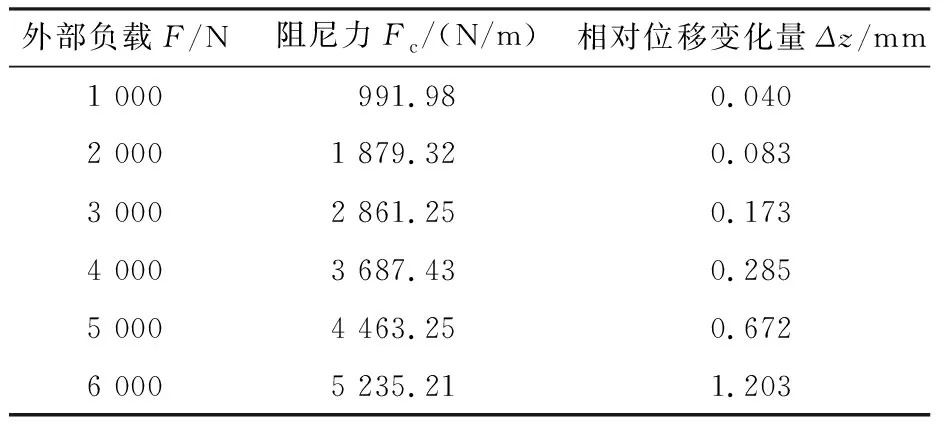
表2 位移相对变化量

通过AMESim仿真实验发现,随着外部负载的增加,车辆悬架减震系统能够提供的有效阻尼明显减少,相对位移变化量明显增强,说明负载的增加降低了车辆悬架减震系统的响应速度和车辆悬架机构的使用性能及减震效果。

本文在表2的基础上,构建了比例系数k的数学模型,并利用MATLAB分析[7-8]且得到了比例系数。

(4)

可得k≈0.35。

由式(4)可知,单一的比例控制环节存在一定的局限性,在进行权值选取与确定时会耗费较长时间,进而降低了减震系统的响应速度。而不能忽略的是实际道路的复杂性,其外部负载处于不规律的连续变化中。因此本文以神经网络算法为基础,提出了单神经网络PID算法,并将其应用于车辆悬架减震系统中,以提高其减震性能与效果。

3 单神经网络PID算法

传统PID控制策略无法实现参数的在线整定,而将单神经网络与PID算法结合起来,实现PID控制器参数的实时整定,弥补了单一比例控制策略的不足,使得车辆具有更强的道路适应性[9-10],其控制框图如图4所示。

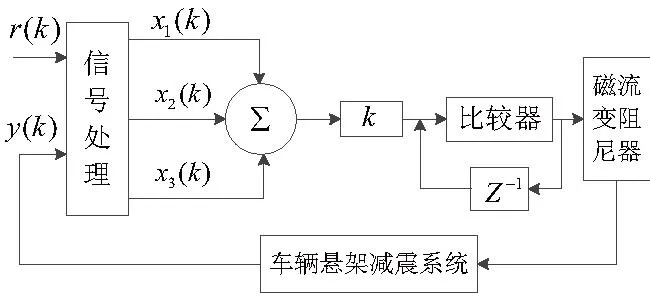
图4 控制系统流程图

对期望值为r(k)与实际输出y(k)进行信号处理并得出单神经元网络所需的3个状态变量x1(k)、x2(k)、x3(k)。

(5)

取k=0.35,控制信号为

(6)

式中ωi(k)为xi(k)的加权系数,主要通过加权系数的调整实现PID参数自适应整定。

采用有监督Hebb学习算法,得

ωi(k+1)=(1-c)ωi(k)+η[e(k)u(k)xi(k)]

(7)

式中:(k)为误差信号;e(k)=r(k)-y(k);c为常数,0≤c≤1,c取0.1。因此权值修正量Δωi(k)可由下式表示:

(8)

控制量u(k)为:

(9)

(10)

ω1(k+1)=ω1(k)+ηPe(k)u(k)x1(k)

(11)

ω2(k+1)=ω2(k)+ηIe(k)u(k)x2(k)

(12)

ω3(k+1)=ω3(k)+ηDe(k)u(k)x3(k)

(13)

式中:比例环节学习速率ηP=0.35;积分环节学习速率ηI=0.2;微分环节学习速率ηD=0.19。

通过PID反馈环节,控制系统成比例释放阻尼力,进而达到稳定系统压力、提高车辆减震系统稳定性的目的。

4 车辆悬架减震系统的优化与仿真

本文运用AMESim软件[11]绘制系统草图、建立子模型、参数设置、运行仿真4个环节,建立减震系统的仿真模型,并进行了仿真实验,得到了相应的特性曲线。

4.1 建立仿真模型

结合图3中1/4悬架的仿真模型,搭建了整个车辆悬架减震的PID控制系统,如图5所示。

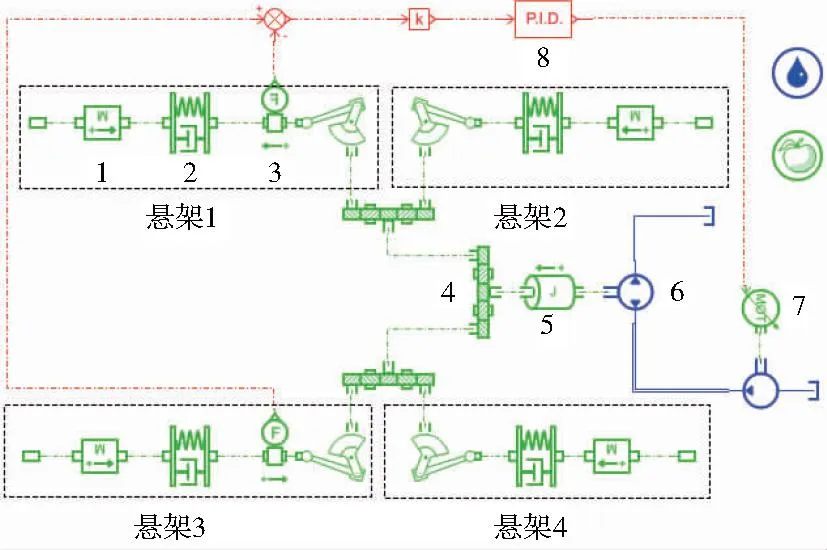
1—簧载质量;2—阻尼系统;3—传感器;4—传动装置;5—传动电机;6—液压马达;7—可调电机;8—PID环节。图5 车辆悬挂减震系统的优化模型

依据表1、图5,本文给出了减震系统仿真模型的基本参数[12],为后续的仿真提供依据,如表3所示。

表3 减震系统仿真模型参数

4.2 系统的仿真与分析

1)系统仿真

a)一般减震系统的特性曲线

本文依据4.1中的仿真模型,按照表3中的参数,进行了不含PID环节的设置并进行仿真,得到相应的特性曲线,如图6所示。

图6 一般减震系统的特性曲线

b)PID控制减震系统的特性曲线

本文依据4.1中的仿真模型,按照表3中的参数将单一神经网络的PID环节应用于图5车辆悬架减震系统并进行仿真,得到相应的特性曲线,如图7所示。

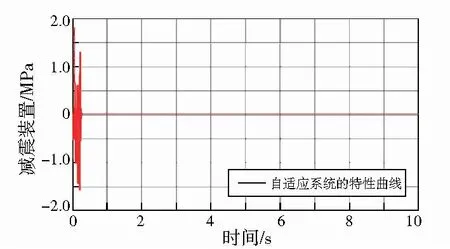
图7 PID控制减震系统的特性曲线

由图6可知,一般减震系统虽然起到了一定的减震效果,但与图7中的PID自适应悬架减震系统相比较,图7中的振动明显进一步减弱。通过实验结果证明,智能减震系统进一步吸收了外部的振动载荷,起到了较好的辅助减震效果。

2)系统分析

依据4.2节1)中的仿真运行结果,分别对二种减震系统的运行结果进行频域分析,并对结果进行比较,分别如图8和图9所示。

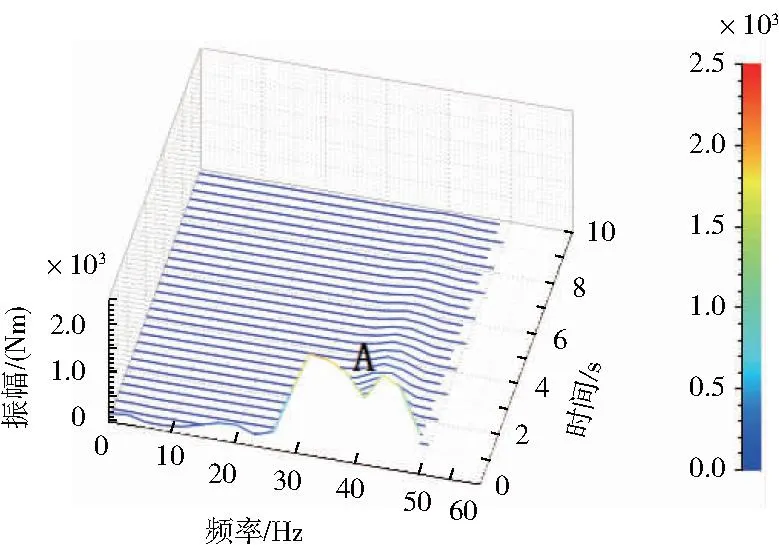
图8 一般减震系统的频域曲线

图9 PID自适应减震系统的频域曲线

通过频域分析发现两种系统在减震开始阶段都出现了较大的振幅。随着时间的推移,一般减震系统逐渐进入稳定工作状态,这时图8中A处的振动虽然减弱,但依然较为明显。而这时,在相同时间与外部振动载荷的作用下,PID自适应减震系统也进入了稳定工作状态,这时将图9中B处的振动状态与图8中A处相比较,发现振动明显进一步减弱。通过分析证明,PID自适应控制系统提高了车辆悬架减震系统的减震效果与稳定性。

5 结语

本文首先分析了车辆悬架的结构与工作原理,并建立了对应的车辆悬架减震系统的数学模型与仿真实验模型。通过分析与仿真发现传统的控制方式,当外部负载连续无规律变化时,车辆悬架减震系统的响应速度较低,影响了车辆悬架的使用性能和减震效果。其次,针对这一问题,文中以传感器、PID控制环节为核心设计了一种具有反馈环节的自适应控制系统,通过PID反馈环节的控制提高减震系统响应速度,进而达到提高减震效果与稳定性的目的。最后,以AMESim为手段搭建了PID自适应控制系统的仿真模型,并进行了仿真实验。通过实验结果的对比分析,表明PID控制系统提高减震系统的响应速度,保持了车辆悬架减震系统所需阻尼力,提高了车辆悬架减震系统运行的可靠性,同时增强了设备的适用性。因此本设计具有一定的应用价值。