融合误跳车的安全仪表系统测试周期优化流程

王海清 毛奇 张鸿志 马佳雯

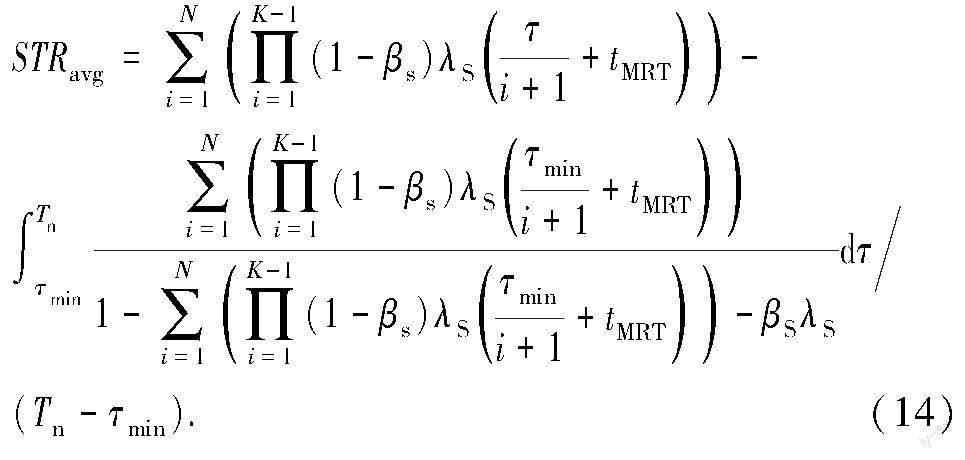
摘要：安全儀表系统（SIS）的验证测试周期对油气生产安全具有重大影响，目前IEC标准推荐的方法仅限于考虑平均需求失效概率的需要，且采用的名义失效率与现场实际不一致。为此提出一种基于贝叶斯估计的融合误跳车影响的测试周期优化流程（PTIST），可以综合考虑SIS运行阶段的误动作和拒动作损失，并通过获取更精确的SIS失效率，实现SIS具体失效数据和数据库信息的结合。将PTIST应用于某加氢裂化装置的液位联锁控制回路中，结果表明：相较于IEC标准，PTIST中的前两个测试周期均缩短，测试周期内的总损失成本平均降低了17.57%，单位损失率平均降低了10.25%，且能有效地利用SIS误跳车信息；PTIST不仅提高了测试周期内SIS的可靠度，而且能大幅降低SIS运行损失成本。

关键词：安全仪表系统； 验证测试周期； 误跳车； 可靠度； 贝叶斯估计

中图分类号：X 937 文献标志码：A

引用格式：王海清，毛奇，张鸿志，等.融合误跳车的安全仪表系统测试周期优化流程［J］.中国石油大学学报（自然科学版），2023，47（6）：130-137.

WANG Haiqing， MAO Qi， ZHANG Hongzhi，et al. Optimization process ofproof test cycle of safety instrumented system integratingspurious trip ［J］. Journal of China University of Petroleum （Edition of Natural Science），2023，47（6）：130-137.

Optimization process of proof test cycle of safety

instrumented system integratingspurious trip

WANG Haiqing1， MAO Qi1， ZHANG Hongzhi2， MA Jiawen1

（1.College of Mechanical and Electrical Engineering in China University of Petroleum（East China）， Qingdao 266580， China;

2.China National Bluestar（Group）Company Limited， Sinochem Holdings， Beijing 100029，China）

Abstract： The proof test cycle of safety instrumented system （SIS） has a significant impact on the safety of oil and gas production. However， the recommended method in the IEC standard is only limited to considering the needs of the average probability of failure on demand， and the nominal failure rate adopted is often inconsistent with the actual situation on site. Therefore， the optimization process of proof test cycle integrating the spurious trip （PTIST） was proposed based on the Bayesian estimation， which could comprehensively consider the spurious trip and failure action loss in the SIS operation stage and by obtaining more accurate SIS failure rate， the combination of SIS specific failure data and database information was realized. The PTIST was applied to the liquid level interlock control circuit of a hydrocracking unit. The results show that， compared with the IEC standard， the first two test cycles in the PTIST are shortened， the total loss cost in the test cycle is reduced by 17.57% on average， the unit loss rate decreased by 10.25% on average， and the spurious trip information can be effectively utilized. The PTIST can not only improve the reliability of SIS during the proof test， butalso greatly reduce the SIS operation loss cost.

Keywords： safety instrumented system; proof test cycle; spurious trip; reliability; Bayesian estimation

安全仪表系统（safety instrumented systm，SIS）是保障油气安全生产的关键设备，通过自动检测危险事件、执行所需的安全动作将工艺装置维持在安全的状态。一旦SIS设备发生故障，装置的动态风险水平就会受到影响［1-2］。为减少SIS拒动作的频率，IEC功能安全标准推荐定期对SIS

进行验证测试，以发现其自诊断功能无法检测到的故障［3］。传统的验证测试周期仅由平均需求失效率（average probability of failure on demand，PFDavg）来决定，但实际生产过程中，SIS的误动作更为频繁，因SIS误动作导致的非计划停车往往导致较大的生产损失及其他安全问题［4］。挪威石油工业协会推荐将误跳车的发生作为验证测试的一部分，利用误跳车信息对验证测试周期进行优化［5］。另一方面，计算测试周期需要能反映生产实际的失效数据。IEC61508认为使用现场失效数据更新的设备失效率比使用工业数据库更可取。鉴于此Brissaud［6］提出了从具有置信区间的现场失效数据中更新设备失效率的计算方法；Kim等［7］提出了适用于SIS的失效模式、影响和诊断分析（failure mode effect and diagnostic analysis， FMEDA）方法用于分割更新后的失效率；刘强等［8］利用贝叶斯估计对安全阀的失效率进行了更新。上述的计算方法受IEC61508标准的引导，往往仅利用了设备现场数据对失效率进行了更新，但由于SIS设备的现场失效数据较少，需借助工业数据库中的设备失效信息（作为先验信息），通过蒙特卡洛模拟补充失效数据。此外为合理地确定、验证测试周期，减少SIS运行中的生产损失，Zhang等［9］提出了油气行业SIS运行周期内的总损失成本计算方法，但该方法中缺少因SIS误跳车导致的生产损失。Torres-Echeverria等［10-11］以PFDavg和SIS运行成本为目标，使用多目标遗传算法对测试策略进行优化，Longhi等［12］综合考虑PFDavg和平均误动作率（average spurious trip rate，STRavg）等因素，以最低生产成本为目标确定测试和维护策略，王海清等［13］在保障SIS风险可控的前提下，实现了对SIS设备测试周期的迭代更新。但这些研究中测试周期的确定均仅以PFDavg为约束指标，忽视了误跳车对测试周期的影响。笔者基于现场失效数据利用贝叶斯方法［14-15］得到更为准确的设备失效率，并针对油气行业提出融合误跳车影响的验证测试周期优化流程，给出误跳车发生后的测试周期确定方法，以期在保障SIS设备安全可靠运行同时，大幅减少设备运行中的当量损失。

1 基于贝叶斯估计的失效率更新

根据现场工程经验SIS各元件的寿命分布服从指数分布，由于SIS的可修性，其抽样分布满足的泊松分布 ［8］ 为

式中，T为SIS失效前的累积运行时间，s；λ为危险失效率；r为失效次数；ti（i=1，2，3，…，r）为设备失效时间，s;n为设备数量。

先验分布选用gamma分布，其概率密度g（λ）为

式中，r0为先验失效次数；T0为SIS先验累积运行时间。

由贝叶斯理论可得

贝叶斯估计采用平方损失函数，则失效率λ的贝叶斯估计λM为

先验分布r0、T0为

式中，χ2为卡方分布；λu为置信度为1-α的危险失效率上限值，可通过查询可靠性数据库获取，若现场失效数据未收集到，可通过蒙特卡洛模拟生成。

2 融合误跳车的测试周期优化流程

为合理的量化误跳车对SIS验证测试周期的影响，不失一般性，推导出融合误跳车影响的KooN冗余结构验证测试周期优化流程（proof test cycle integrating the spurious trip，PTIST），该流程满足数学假设： ①安全仪表系统各元件失效率恒定；②不考虑验证测试所需时间，因其远小于验证测试周期；③验证测试能够完全检测到设备隐性故障，且对每个子系统同时进行，维修后可视为与新的一样好；④SIS各元件的初始状态均处于功能最佳状态；⑤危险可检测到的失效对SIS误跳车無影响。

基于上述假设，测试周期优化流程步骤为：①以所需PFDavg为约束指标确定测试周期τm;②以STRavg为约束指标确定测试周期τn;③分别计算τm与τn周期内的当量损失γall，将γall与厂区能承受的当量损失上限γmax进行比较；若γall≤γmax，选取τm为第一个测试周期，反之，比较τn时间段内的当量损失与γmax，判断标准同上，第一个测试周期记为τmin;④以τmin为起点，迭代更新计算下一个测试周期Tmin，判断方法同步骤③;⑤若测试周期内发生误跳车，则根据具体的误跳车信息对测试周期进行调整;⑥将PTIST与IEC确定的测试周期内的当量损失及执行测试前的SIS可靠度进行对比。

2.1 测试周期τm确定

SIS由传感器（sensor element，SE）、逻辑控制器（logic controller，LC）、执行元件（final executor，FE）3部分组成，对于完全验证测试的KooN冗余系统，单个子系统测试周期τm时间段内的PFDavg为

式中，β为未检测到的危险失效的共因失效系数；tMRT为平均维修时间；λDU为更新后的未检测到的危险失效率;τm为验证测试周期，通常由所需的PFDavg确定；τ为实际验证测试时间;K为需要执行安全功能的通道数；N为整体可用的通道数。

SIF回路的PFDavg为

PFDavgSIS=PFDavgLC+PFDavgSE+PFDavgFE.（9）

式中，PFDavgSE、PFDavgLC和

PFDavgFE分别为传感器子系统、逻辑控制器子系统和执行元件子系统的平均需求失效率。

2.2 测试周期τn确定

KooN冗余结构单个子系统在τn时间段内的STRavg为

式中，βS为安全失效的共因失效系数；λS为更新后的安全失效率；τn为由STRavg确定的验证测试周期。

由误跳车导致的KooN结构的SIF回路的STRavg并不是将3个子系统简单加和，当传感器子系统发出误跳车信号时，当且仅当后边两个子系统均正常运行，才会导致SIF回路发生误跳车，一种新的STRavg计算框架［16］可以表示为

STRavgSIS=STRavgSE（1-PFDavgLC）（1-PFDavgFE）+STRavgLC（1-PFDavgFE）+STRavgFE.（11）

式中，STRavgLC、STRavgSE和PFDavgFE分别为传感器子系统、逻辑控制器子系统和执行元件子系统的平均误动作率。

2.3 当量损失计算

由式（8）～（11）可确定τm和τn，首先计算出τm时间段内的STRavgSIS和PFDavgSIS，τm内SIS的当量损失为

式中，γall为SIS拒动作和误动作的当量损失之和；λde为工艺需求率；γPFD为拒动作导致的当量损失；γSTR为误动作导致的当量损失；γm为拒动作导致的财产损失；γp为拒动作导致的人员伤亡损失；M为人员伤亡数量；γT为停产损失；D为停产天数；γn为误动作导致的财产损失。

2.4 迭代计算下一个测试周期

SIS单个子系统在τmin至Tm时间段内的PFDavg为

式中，Tm为由所需PFDavg确定的第二个验证测试周期。

同样单个子系统在τmin至Tn时间段内的STRavg为

式中，Tn为由STRavg确定的第二个验证测试周期。

由式（13）～ （14）可确定Tm和Tn，根据相同的判定方法得到第二个验证测试周期Tmin，且可推导出第i个验证测试周期，由式（12）可得第i个测试周期内的当量损失。

2.5 測试周期更新

根据具体误跳车信息更新测试周期。以传感器子系统为例，t（t<τmin）时刻发出误跳车信号导致SIF回路发生误跳车，若τmin=τm，则传感器子系统在τminup时间段内的PFDavgSE为

式中，τminup为调整后的测试周期。

由式（8）可得逻辑控制器和执行元件在τminup内的PFDavg，结合式（9）和（15）可确定τminup。

若τmin=τn，则传感器子系统在τminup时间段内的STRavgSE为

由式（10）可确定STRavgFE与STRavgLS，结合式（11）和（16）可确定τminup。同理可推断出SIF回路在T（τmin

PTIST的计算流程如图1所示。

当量损失由步骤（3）可得，KooN冗余SIS设备可靠度R（τ）为

3 工程应用

加氢裂化成为油气行业中油品质量升级和原油高效加工的关键技术之一，其工艺流程如图2所示。

油气分离装置中热高压分离器的液位联锁保护回路可靠性如图3所示。该SIS由三取二（2oo3）表决结构的液位传感器、外部总体视为一取一（1oo1）表决结构的逻辑控制器和二取一（1oo2）表决结构的执行元件构成。

其主要的功能之一为反应器的液位达到预设高触发或低触发值时，逻辑控制器发送关断信号给执行元件，执行元件打开或关闭控制阀门，保证反应器内液位处于安全可控的水平。

表1为工业数据库中的液位联锁保护回路相关设备失效数据（传感器、逻辑控制器与执行元件的平均维修时间分别为8 、12和24 h）。不失一般性，假设保护层分析报告显示：该液位联锁回路的安全完整性等级（safety integrity level，SIL）需满足SIL2要求。

依据某炼化企业提供的现场联锁当量损失数据，假定SIS拒动作导致的财产损失为600万元，人员伤亡损失γp为100万元，人员伤亡数为2，停产损失γT为400万元，停产3 d（测试周期的确定仅与

PFDavg或STRavg有关，因而数据的选取并不影响后续计算得出的结论），工艺需求率［17］为1.14×10-4 h-1。误跳车导致的财产损失γn为100万元，每年厂区能承受的当量损失为20万元，综合考量误跳车发生后的经济损失及安全风险［18］，该联锁回路的误动作等级（spurious trip level，STL）为STL2（0.001≤STRavgSIS<0.01）。

由于SIS设备的高度可靠性，针对液位联锁保护回路通过生产收集与蒙特卡洛模拟相结合得到5组型号相同、工况大致一样的样本数据（每组20个），分别记为样本1～5。以样本1的执行元件为例，其主要的失效模式为无法打开（fail to open，FTO），近6年内的现场失效数据为6806、18213、26841、38401和49278 h。通过蒙特卡洛的模拟，生成50个（0～1）区间内的均匀随机数，代入失效分布函数的逆函数中，计算出一系列失效时间，截取其中15个数据，部分模拟生成数据为56419、68251、74496、82201 和100781 h 。

分别对传感器、逻辑控制器和执行元件进行FMEDA分析，安全失效约占总的失效模式的55%，危险失效约占总失效模式的45%。结合FMEDA分析结果和表1，由式（6）～（7）即可对设备失效率进行更新，更新结果见表2。此外将文中方法与SINTEF［19］ 提出的失效率更新方法进行对比，以样本1～5中执行元件为例，计算结果的平均相对误差为2.8%，但SINTEF中计算结果准确度受设备失效数量的影响。

IEC标准以PFDavg作為确定SIS验证测试周期的约束指标，以样本1为例，由式（8）～（9）可得，此约束指标下测试周期τm为10380 h。实际生产中SIS误跳车相对于拒动作更加频繁，确定验证测试周期时将误跳车考虑在内更符合工程实际。

由式（10）～（11）可得，以STRavg为约束指标确定的测试周期τn为9250 h，且τm时段内γall>γmax，τn时段内γall<γmax，故选取τn为第一个测试周期。在得到样本1的第一个测试周期后，根据式（13）～（14）可实现测试周期的迭代更新。计算结果表明，Tn（14580 h）内γall<γmax，Tm（16750 h）内γall>γmax，选取Tn作为第二次测试周期，相应计算结果见图4（a）。同理计算其余样本的测试周期，结果如图4（b）所示。

由图4可知，样本2中τn与τm的差值（1240 h）、Tn与Tm的差值（2340 h）均为最大，若仅以PFDavg为约束指标，τm和Tm周期内的SIS当量损失均会超过γmax。以样本2为例，τm周期内的当量损失为27.055万元，γmax为25.890万元；Tm内的当量损失为43.424万元，γmax为40.959万元。样本第一、二个测试周期均分别由τn和Tn确定。样本测试周期及损失成本对比（以PFDavg为约束指标的计算结果为基准）见表2。表2中，SE表示传感器、LC表示逻辑控制器、FE表示执行元件。

由表2可知，相对于IEC标准，PTIST第一个测试周期τn平均缩短1162 h，计算平均误差为10.95%；第二个测试周期Tn平均缩短2 222 h，计算平均误差为13.06%。按照PTIST的计算结果开展验证测试活动，可以降低厂区生产损失。由式（12）计算可得：仅考虑PTIST中前两个测试周期，其总当量损失平均降低了26.93%，单位损失率平均降低了15.98%，且前两个测试周期内的γall均未超出γmax。

厂区维修记录显示，传感器元件发出误跳车信号导致该液位联锁保护回路分别在8760和10950 h时发生误跳车，班组维修后可以视为对传感器元件执行了验证测试。由于τmin=τn，根据式（16）对表2中的计算结果进行调整，并与IEC标准进行对比，调整后的测试周期τminup及损失成本对比见表3。由表3可知，相对于IEC标准，PTIST调整后第一个测试周期平均缩短772 h，计算平均误差为7.37%，第二个测试周期平均缩短1402 h，计算平均误差为8.21%。调整后前两个测试周期内的总当量损失平均降低了17.57%，单位损失率平均降低了10.25%。由表2、3中的计算结果可得：PTIST可结合具体的误跳车信息对测试周期进行调整，且调整前、后前两个测试周期内的SIS总当量损失和当量损失率均大幅降低。

以表3调整后的测试周期为基准，可得不同计算流程下SIS的需求失效概率（PFD）与误动作率（STR）随时间变化曲线，以样本1为例，如图5所示。

由图6可得，PTIST能够提高维护人员对SIS进行验证测试时的设备可靠度。与传统方法相比，PTIST不仅有效帮助厂区减少SIS运行过程产生的当量损失，而且能够提高测试周期内SIS的可用性与安全性。

由图5可知，与传统的IEC标准相比，PTIST能够降低测试周期内SIS的PFD与STR的最大值，这意味着SIS的安全性和可靠性均有所提高。由式（17）可求得SIS的可靠度随时间变化曲线，以样本1为例，如图6所示。

4 结 论

（1）对现场失效数据进行FMEDA分析后，结合贝叶斯估计与蒙特卡洛模拟得到SIS失效率，在提高验证测试周期计算准确性的同时有助于企业建立自己的失效数据库。

（2）原IEC标准中测试周期的确定仅与PFDavg有关，按照提出的KooN冗余结构的测试周期优化流程PTIST执行测试时SIS的可靠度更高，测试周期内的总当量损失和单位损失率更低； PTIST可结合具体的误跳车信息对测试周期进行调整，符合企业生产实际的需要。

（3）实际生产中的验证测试并不能完全发现SIS的隐性故障，在今后的研究中可以考虑部分测试中的测试覆盖率对确定测试周期的影响。

参考文献：

［1］ LUNDTEIGN M A， RAUSAND M. Commoncause failures in safety instrumented systems on oil and gas installations： implementing defense measures through function testing ［J］. Journal of Loss Prevention in the Process Industries， 2007，20（3）：218-229.

［2］ 王海清，乔丹菊，刘祥妹，等.KooN表决结构多阶段马尔可夫模型简化算法［J］.中国石油大学学报（自然科学版），2017，41（6）：147-153.

WANG Haiqing， QIAO Danju， LIU Xiangmei， et al. A simplified multi-phase Markov model with KooN structure［J］. Journal of China University of Petroleum（Edition of Natural Science）， 2017，41（6）：147-153.

［3］ CAI B P， LI W C， LIU Y H， et al. Parameter uncertainty modeling of safety instrumented systems ［J］. Petroleum Science， 2021，18（6）：1813-1828.

［4］ LUNDTEIGN M A， RAUSAND M. Spurious activation of safety instrumented systems in the oil and gas industry： basic concepts and formulas ［J］. Reliability Engineering & System Safety， 2008，93（8）：1208-1217.

［5］ The Norwegian Oil Industry Association. Application of IEC 61508 and IEC 61511 in the Norwegian petroleum industry ［R］. Stavanger： The Norwegian Oil Industry Association，2004：142-146.

［6］ BRISSAUD F. Using field feedback to estimate failure rates of safety-related systems ［J］. Reliability Engineering & System Safety， 2017，159：206-213.

［7］ KIM S K， KIM S Y. An evaluation approach using a HARA and FMEDA for the hardware SIL ［J］. Journal of Loss Prevention in the Process Industries， 2013，26：1212-1220.

［8］ 劉强，包士毅，罗利佳，等.基于贝叶斯估计的RBI在安全阀校验周期确定中的应用［J］.压力容器，2016，33（4）：52-58.

LIU Qiang， BAO Shiyi， LUO Lijia， et al. Application of RBI in determining inspection period of safety valve based on Bayesian method ［J］. Pressure Vessel Technology， 2016，33（4）：52-58.

［9］ ZHANG A B， ZHANG T L， BARROS A， et al. Optimization of maintenances following proof tests for the final element of a safety-instrumented system ［J］. Reliability Engineering & System Safety， 2020，196：106779.

［10］ TORRES-ECHEVERRIA A C， MARTORELL S， THOMPSON H A. Modelling and optimization of proof testing policies for safety instrumented systems ［J］. Reliability Engineering & System Safety， 2009，94（4）：838-854.

［11］ TORRES-ECHEVERRIA A C， MARTORELL S， THOMPSON H A. Design optimization of a safety instrumented system based on RAMS+C addressing IEC 61508 requirements and diverse redundancy ［J］. Reliability Engineering & System Safety， 2009，94（2）：162-179.

［12］ LONGHI A E B， PSAAOA A A， GARCIAC P A A. Multiobjective optimization of strategies for operation and testing of low-demand safety instrumented systems using a genetic algorithm and fault trees ［J］. Reliability Engineering & System Safety， 2015，142：525-538.

［13］ 王海清，毛奇，李敏睿，等.化工安全仪表系统失效率与检测周期迭代算法［J］.中国石油大学学报（自然科学版），2021，45（4）：131-138.

WANG Haiqing， MAO Qi， LI Minrui， et al. Iterative algorithm of failure rate and proof test cycle of chemical safety instrumented system ［J］. Journal of China University of Petroleum（Edition of Natural Science）， 2021，45（4）：131-138.

［14］ 程凯凯，姚继涛，程正杰，等.基于相关性与贝叶斯推断的管道腐蚀深度预测方法［J］.油气储运，2021，40（8）：854-859.

CHENG Kaikai， YAO Jitao， CHENG Zhengjie， et al. Prediction method of pipeline corrosion depth based on the correlation and Bayesian inference ［J］. Oil & Gas Storage and Transportation， 2021，40（8）：854-859.

［15］ 徐后佳，帅健，杨敬东，等.城镇燃气管道事故动态贝叶斯网络情景推演及模拟［J］.油气储运，2022，41（8）：900-907.

XU Houjia， SHUAI Jian， YANG Jingdong， et al. Deduction and simulation of DBN scenarios in urban gas pipeline accidents ［J］. Oil & Gas Storage and Transportation， 2022，41（8）：900-907.

［16］ 王海清，喬丹菊，冯军，等.石化装置安全仪表系统KooN表决结构的误跳车率定量分析［J］.中国安全科学学报，2018，14（12）：153-157.

WANG Haiqing， QIAO Danju， FENG Jun， et al. Quantitative analysis on spurious trip rate of safety instrumented system with Koon voting architectures in petrochemical plant ［J］. China Safety Science Journal， 2018，14（12）：153-157.

［17］ ALIAZADEH S， SRIRAMULA S. Reliability modelling of redundant safety systems without automatic diagnostics incorporating common cause failures and process safety demand ［J］. ISA Transactions， 2017，71（2）：599-614.

［18］ 戚萌.化工装置安全仪表系统的误动作及设计优化研究［D］.青岛：中国石油大学（华东），2019.

QI Meng. Study on the spurious activation and design optimization of safety instrumented systems in chemical plants ［D］. Qingdao： China University of Petroleum （East China）， 2019.

［19］ HAUGE S，LUNDTEIGN M A. Guidelines for follow-up of safety instrumented systems（SIS） in the operating phase［R］. Trondheim： SINTEF， 2008.