深度学习与Eaton法联合驱动的地层孔隙压力预测方法

许玉强 何保伦 王舒 韩超 肖凡 管志川 刘宽

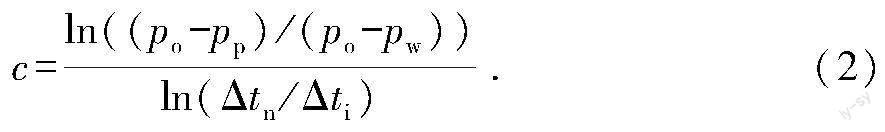
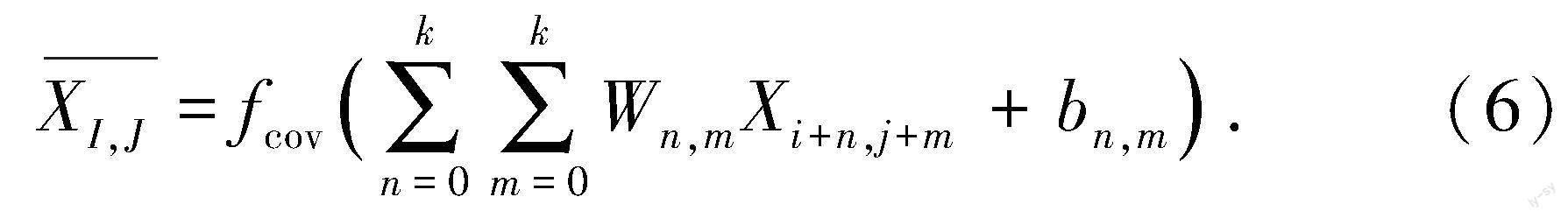
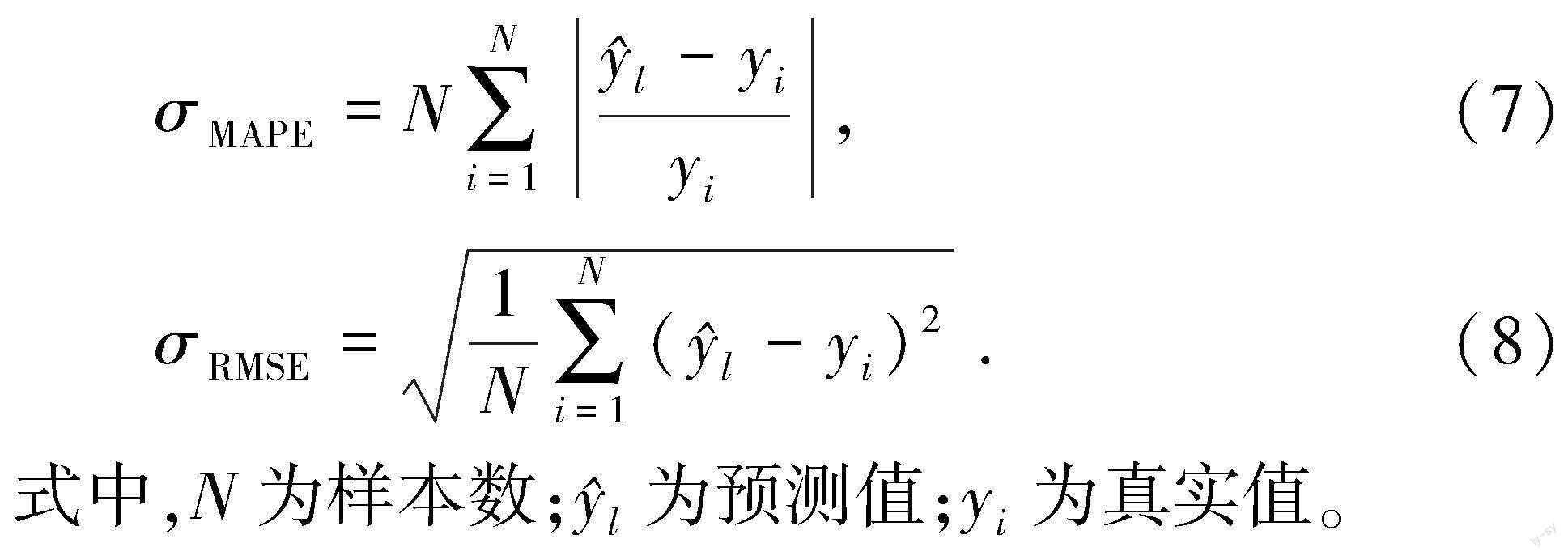
摘要：海上深部復杂地层孔隙压力的精确预测一直以来是钻井工程面临的难题之一。针对传统Eaton法的局限性和现有数据驱动法的不足，通过构建地层压力实测点的扩充方法，构建卷积神经网络（convolutional neural network， CNN）和长短期记忆网络（long short term memory， LSTM）组合模型，充分挖掘钻测录震多源数据与Eaton指数之间的复杂非线性关系，可基于区块内已钻井的有限实测地层压力数据，实现全井Eaton指数的精细预测，为新探区地层压力实测点较少且分布不均等条件下地层孔隙压力的准确预测提供有效手段。结果表明：建立的方法预测深部复杂地层孔隙压力的平均相对误差为2.70%，而传统Eaton和LSTM方法的平均相对误差分别为7.60%和5.12%；通过深度学习与Eaton法联合驱动，不但提高了深部复杂地层孔隙压力的预测精度，也为传统方法融入了多源数据响应特征，为数据驱动方法提供了理论支撑。

关键词：Eaton法； 数据驱动； 深度学习； 地层孔隙压力

中图分类号：TE 21 文献标志码：A

引用格式：许玉强，何保伦，王舒，等.深度学习与Eaton法联合驱动的地层孔隙压力预测方法［J］.中国石油大学学报（自然科学版），2023，47（6）：50-59.

XU Yuqiang， HE Baolun， WANG Yanshu， et al. A novel prediction method of formation pore pressure driven by deep learning and Eaton method ［J］.Journal of China University of Petroleum（Edition of Natural Science），2023，47（6）：50-59.

A novel prediction method of formation pore pressure driven

by deep learning and Eaton method

XU Yuqiang1，2， HE Baolun1，2， WANG Yanshu3， HAN Chao3，

XIAO Fan4， GUAN Zhichuan1，2， LIU Kuan1，2

（1.National Key Laboratory of Deep Oil and Gas（China University of Petroleum （East China））， Qingdao 266580，China;

2.Shandong Ultra-Deep Drilling Process Control Engineering Technology Research Center， Qingdao 266580， China;

3.SINOPEC Matrix Corporation， Qingdao 266000， China;

4.Development Division of PetroChina Southwest Oil and Gas Field Company， Chengdu 610000， China）

Abstract： The accurate prediction of formation pore pressure in deep complex formations has been one of the challenges in drilling engineering. In this paper， the limitations of the traditional Eaton methods and the shortcomings of the existing data-driven methods were discussed， and a convolutional neural network （CNN） and short-term memory network （LSTM） combination model was constructed to fully explore the complex nonlinear relationship between drilling and recorded multi-source data and Eaton index by constructing an extension method for measuring formation pressure points. Based on the limited formation pressure data measured in drilled formations， a precise prediction of the Eaton index of the entire well can be achieved， which can provide an effective means for accurate prediction of the formation pore pressure in new wells with few measured points and uneven distribution of formation pressure. Field case studies show that the average relative error of the method established for predicting pore pressure in deep complex formations is 2.70%， while the average relative error of the traditional Eaton and LSTM methods is 7.60% and 5.12%， respectively. The combination model of deep learning with Eaton method， not only can improve the prediction accuracy of deep complex formation pore pressure， but it can also integrate multi-source data response features into the traditional methods， providing a theoretical support for the data-driven methods.

Keywords： Eaton method; data-driven; deep learning; formation pore pressure

准确预测地层孔隙压力是保障钻井工程设计合理性、降低钻井工程风险的关键技术之一［1-3］。目前常用的地层孔隙压力预测方法有Eaton法、等效深度法、Bowers、Fillippone法等，对于不同地层和成压机制，不同方法有各自的优势［4-7］。Eaton法是目前较常用的地层孔隙压力预测方法，其综合考虑了压实作用，并总结和参考了钻井实测压力与各种测井信息之间的关系，是一种比较实用的方法［8］。实践表明，Eaton法预测准确与否的关键在于正常压实趋势线的建立和Eaton指数的选取，其中可依据泥质含量等信息得到较为准确的正常压实趋势线［9］。而随着钻遇地层越来越复杂，难以用单一的Eaton指数获得全井段理想的预测结果。为此，Shi等［10］提出了一种考虑不同地层计算区域指标的“分层Eaton法”。但由于Eaton指数反算需要实测地层压力，而受限于成本等原因，现场一般很少测量不同地层的压力数据（多集中在储层及以上地层），导致该方法的应用受到了一定限制。另一方面，由于Eaton法本身模型和参数的局限性，对于深部复杂地层（如非泥岩地层、岩性变化大的地层等），预测结果难以适应深部复杂地层的需求。随着人工智能技术和钻井大数据的发展，机器学习算法被引入地层压力预测中［11-12］。李春茂等［13］引入梯度提升回归树算法（gradient boosting regression tree，GBRT）分析7种测井资料与地层孔隙压力建立相关性，对地层孔隙压力进行预测。Matinkia等［14］通过测井数据对多种模型进行验证，结果表明CNN模型在特征提取上具有很大的优势。宋先知等［15］就组合LSTM和BP模型展开研究，将两口井的地层孔隙压力作为训练集、一口作为验证，证明了该模型的可行性和准确性。通过分析发现，对于一口井乃至一个区块，实测地层压力数据十分有限，如何获得足够数量和质量的地层压力样本用于模型训练是该方法面临的一个难题；另一方面，目前数据驱动方法仅分析数据间的复杂非线性关系，缺乏Eaton法等常规方法的理论支撑（如欠压实理论等），若在分层Eaton指数方法的基础上融入数据驱动（深度学习）方法对Eaton指数进行富含测井响应特征的预测，有望在保持模型稳定性的前提下，充分考虑不同测井数据、地震数据的响应特征，从而进一步提高深部复杂地层压力的预测精度，也可弥补目前数据驱动方法由于小样本导致的模型泛化能力低、稳定性不佳的难题。为此，笔者提出CNN-LSTM深度学习与Eaton法联合驱动的地层孔隙压力预测方法，在丰富地层压力实测值（样本）的基础上，实现传统Eaton法、分层Eaton指数、测震录多源数据、机器学习算法的深度融合，为传统方法融入多源数据响应特征，也为数据驱动方法提供理论支撑。

1 分层Eaton指数预测地层孔隙压力方法

1.1 常规Eaton法

1975年国外学者Eaton提出了利用声波资料预测地层孔隙压力的Eaton公式［16］，该方法不仅考虑了压实作用和异常高压的成因，还考虑了实测压力和测井资料之间的关系。其计算模型为

pp=po-（po-pw）（Δtn/Δti）c.（1）

式中，pp为地层孔隙压力，MPa；po和pw分别为上覆地层压力和地层水静液柱压力，MPa；Δtn和Δti分别为该深度点正常趋势线上的声波时差和实测声波时差，μs/m；c为Eaton指数。

Eaton法预测地层孔隙压力的关键在于正常压实趋势线的建立和Eaton指数的选取。其中建立正常压实趋势线需要选取正常压实区间，主要以厚层泥岩、页岩或泥页岩为主，在现场实践中可依据测井解释的泥质含量确定。对于横向构造不复杂的区块，常取多口已钻井的平均值作为该区块的正常压实趋势线。

Eaton指数是与地质构造、地质年代、流体性质、岩石性质等有关的經验性参数，需要根据实测地层孔隙压力资料求取：

1.2 分层Eaton指数法

根据层序地层学原理，同一区块同一层组内岩性和地质状况相似［17］。因此在同一层组深度范围内Eaton指数的数值虽然具有随机性、模糊性，但是其值相差不大，散落在一个定值（均值）附近的分布区间内（方差），即可以用正态分布状态来描述Eaton指数在某地层内的分布情况［18］。其概率密度函数P（x）

和累积概率分布函数F（x）表达式为

式中，u为Eaton指数均值;σ为标准差。

在现场实践中可以用Eaton指数分布函数的均值代表该层组的Eaton指数，采用不同地层层组（按地震界面划分）取不同Eaton指数的方法，以提高Eaton法的预测精度和复杂地层的适应性。

以南海某区块为例，该区块具有深部地层高温高压、地层情况复杂的特点，由于成压机制较复杂，常规Eaton法在该地区深部复杂地层中的适用性和预测准确性较差。该地区已钻井8口，由于区块横向地层差异性较低且中浅部地层压力发育正常，实践表明采用该区块的平均正常压实趋势线即可满足工程需求：ln（Δtn）=-0.0003H+5.0857，其中H为测深，m。地层孔隙压力实测点（主要通过测压取样和关井求压测得）以及Eaton指数反演情况如表1所示。利用式（3）得到各地层层组Eaton指数的分布情况如表2和图1所示。其中层组1、2、3由于各仅有1个实测数据，以该点实测数据反演值作为本层组的Eaton指数。

由图1可知：Eaton指数随地层深度的增加而整体增大，但井深越大其分布越不集中（不确定性增强），若Eaton指数在某地层中的分布过于分散，其均值将无法代表该地层的实际情况，这就对深部地层Eaton指数的准确选取带来了困难。

为了对比不同Eaton指数选取方式条件下地层孔隙压力预测的准确性，针对该区块已钻井A井，取如下3种情况进行对比分析：①全井采用唯一Eaton指数（区块平均值）；②分层选取Eaton指数，假设层组6（3967～4098 m）缺失实测数据，与层组5选取相同值；③分层选取Eaton指数。其对比结果如图2所示。

由图2可知：分层Eaton法可大幅提升复杂地层的适用性和准确性，地层分层越多，各分层内选取的Eaton指数越准，该方法预测的地层压力准确性越高。

2 CNN-LSTM深度学习与Eaton法联合驱动方法

2.1 现有数据驱动方法

机器学习算法在解决复杂非线性多维问题上具有很大的优势，比如石油领域中测井曲线重构［19］、地震反演［20］、产量预测［21］等。通过调研分析发现，目前的相关研究主要集中在探讨机器学习模型的适用性以及利用模型分析测井等数据与地层压力之间的关系上，研究的基础是假设用于训练的地层压力为真实压力。实际上对于一口井乃至一个区块，实测地层压力的数据十分有限，尤其是新探区，探井数量少，有限的测压点也一般集中于储层附近地层，难以反映上部地层压力对测井等数据的响应特征，导致训练模型对上部地层的适应性和可靠性差。

2.2 实测点扩充方法

通过分析地层压力实测点的规律（表1），在地层岩性变化不大的条件下，邻近几十米范围内的地层孔隙压力实测值基本相等。因此提出了依据自然伽马、声波时差等测井数据变化率和岩性界面的实测点扩充方法，具体步骤如下：

（1）归一化处理考虑到不同测井数据之间量纲的影响。将测井数据归一化处理到0～1，归一化后测井数据yi表达式为

式中，yi为对应深度Hi处第i种特征的归一化测井数据；xi为实测深度Hi处第i种特征的原始测井数据。

（2）一次初步扩充井深范围为H0±25 m（H0为实测点深度，由于不同地区地质条件不同，需要根据实际统计分析情况具体确定），认为该深度段上下地層孔隙压力当量密度相等，这往往未能充分考虑岩性变化对地层压力的影响。二次扩充以归一化的测井数据变化为依据（具体流程见图3），其变化率ki可以表示为

式中，ki为变化率阈值，本文中取0.1（阈值推荐范围为0.07～0.15，阈值选取越大样本量越多，但输出精度越低）。不同测井数据下自然伽马（GR）、钻速、随钻电阻（P40H、P28H、P16H）、声波时差（DTCO）、岩石密度（RHOB）的变化率应该满足最大值小于阈值，满足式（5）连续数组y1、y2、…、y0、…、yi其对应深度H11、H21、…、H01、…、Hi1。

（3）限制条件。考虑到断层、岩性界面等特殊构造会引发异常地层压力［22］，因此在进一步优选深度范围时应该尽量避开断层及岩性界面。优化后深度为H12、H22、…、H02、…、Hi2。

用上述方法对南海某区块8口已钻井实测点47个（深度步长为1 m）进行扩充，如图4所示，即使邻近区域（③和④点相距11 m），若岩性界面或测井曲线发生较大变化，其实测地层压力也会波动（3872 m处实测地层压力当量密度为1.64 g/cm3， 3883 m处为1.74 g/cm3），反之，①②③点或④⑤点，在岩性和测井数据波动不大的情况下，井深相差10～20 m，但实测地层压力当量密度仅相差0.02 g/cm3。E井3872 m深度处利用变化率初步选取ΔH11对应3840～3875 m，考虑到3899 m处岩性界面的影响，在深度优化为ΔH12对应3860～3875 m深度段实测地层孔隙压力当量密度为1.63 g/cm3。以此类推，可将整个区块实测点扩充至1522个，增幅31.38倍。

2.3 基于CNN-LSTM深度学习的Eaton指数精细反演方法

Eaton法在分层足够多、各分层Eaton指数取值足够准的条件下其预测结果十分理想。据此提出利用区域录井、测井、地震、压力实测等多源数据基于深度学习算法的Eaton指数精细反演方法。

2.3.1 CNN-LSTM模型构建

CNN用作特征（融合）提取，然后将输出的feature映射为序列向量输入到LSTM当中［23］。首先，采用分层提取方法使设计的网络结构和二维卷积核函数自动提取序列的空间特征；其次，优化LSTM网络模块来减少网络对数据的长时间依赖；最后，在端对端模型的训练过程中，引入Adam优化算法，加快权重的拟合并提高网络输出的准确性和鲁棒性。

（1）卷积神经网络。CNN是一种深层前馈网络，常用于处理多个阵列数据［24］，是一种经典的深度学习方法，是一种有效的复杂非线性模型建模工具，在多维数据处理上具有优势。CNN卷积层特征图的输出为

式中，Xi+n，j+m为输入矩阵n行m列的值；fcov（*）为激活函数；Wn，m为卷积核的权重；bn，m为卷积核偏差；k为滑动窗口大小。

（2）长短期记忆模型。LSTM是一种时间递归神经网络［25］，可以较好地分析时间序列数据间的依赖关系，因此本文中提出深度学习模型将CNN与LSTM相结合，图5为本文中提出的深度学习模型。为了验证其精准性，该模型包含输入层、卷积运算层、池化层、展平层、LSTM层、全连接层、输出层。其中输入层参数为大钩载荷、泵压排量、层速度、自然伽马、声波时差等13个特征与Eaton指数进行训练。通过指标平均绝对误差百分比σMAPE和均方根误差σRMSE对其评价，

式中，N为样本数；l为预测值；yi为真实值。

2.3.2 基于Pearson相关系数和最大信息系数筛选特征参数

Pearson相关系数是比较经典的计算方法［26］。其相关系数的取值为［-1，1］，相关系数的绝对值越大，说明两组随机变量的相关性越强。最大信息系数（maximal information coefficient， MIC）用于衡量两个变量X和Y之间的关联程度，线性或非线性的强度，相对常规的Pearson相关性分析，MIC更加适用于复杂非线性性关系，且具有计算复杂度低，鲁棒性更高的优点。MIC相关系数的取值为［0，1］，越接近1相关性越强，Eaton指数与其他特征相关系数见表3。

为了选出相关性更强的特征，结合上述两种方法对现有的19种特征进行相关性分析。

MIC更能表征这种强非线性关系，将其相关系数小于0.35定义为弱相关性，并将钻速、钻压、钻盘转速、扭矩、出口钻井液温度5个特征剔除，因此使用其余14个特征进行训练。

2.3.3 计算分析

采用南海某区块进行Eaton指数训练验证和测试，通过数据样本扩充，1522组扩充后的数据其深度步长为1 m，为了与测井数据的深度步长（0.1 m）统一，将1522组数据的深度步长统一调整为0.1 m，这样总共就有（1522×10×14）个数据样本。然而A井作为验证井不参与训练，训练样本为（14720×14），即90%用于训练集，后10%用于数据模型测试集，采用MATLAB编程，其自带多种运算库，在数据处理上具有强大的优势。由于不同的模型参数对其预测结果有很大影响，因此采用正交试验的方法［27］对模拟参数进行优化。前期预训练试验结果表明，当输入序列长度为0.1、dropout参数为0.2、训练迭代轮数为50、CNN卷积层数为6时模型能达到较好的效果，采用正交试验方法，对模型CNN卷积核数（32、64、128、180）、LSTM隐含层神经元个数（32、64、128、180、）、输出层（64、128、180、256）、激活函数（relu、tanh、elu、sigmoid）共81种模型参数组合进行优选，不同模型参数的测试结果见表4。同理对LSTM模型进行优化并与CNN-LSTM模型预测对比。

2.3.4 预测结果对比

从表4的预测结果可以看出，其中第4组试验结果σMAPE、σRMSE最小，其说明在该组合参数下其预测结果能达到该模型的最优，图6为最优组合下的训练真实值与预测值。0～2000 m各种方法下的Eaton指数对预测结果误差影响较小，其按照层组1统计结果取0.5，因此主要针对2000～4050 m地层Eaton指数进行预测。

假设目标井层组6实测点缺失，在训练样本中缺乏此深度段数据，以此来分析该模型对Eaton指数预测精准性，如图7所示，分别对分层取Eaton指数、CNN-LSTM模型预测Eaton指数、LSTM模型训练Eaton指数进行对比，其对应结合Eaton模型对地层孔隙压力预测如图8所示。

如图8所示，3种方法在深度小于2000 m地层中预测结果与实际值相差不大，而对深部深度地层无法准确预测，LSTM模型预测结果也无法精准预测，而本文中提出的CNN-LSTM深度学习的方法能有效进行多维特征提取，与传统Eaton机制相结合的新方法能有效预测。利用实测地层压力对3种方法的预测误差进行对比分析，结果如表5所示。通过实测点的标定，CNN-LSTM深度学习与Eaton模型结合的方法平均相对误差为2.7%（最大为609%，最小为0.32%），而传统分层Eaton法、LSTM方法和LSTM-Eaton模型方法的平均相对误差分别为760%（最大为10.73%，最小为4.78%）、6.60%（最大為10.45%，最小为1.57%）和5.12%（最大为9.82%，最小为0.67%）。

3 结 论

（1）在保持模型稳定性的前提下，充分考虑不同测井数据、地震数据的响应特征，提出了CNN-LSTM深度学习与Eaton法联合驱动的地层孔隙压力预测方法，该方法弥补了目前数据驱动方法由于小样本导致的模型泛化能力低、稳定性不佳的问题。

（2）依据自然伽马、声波时差等测井数据变化率和岩性界面，确定实测点扩充井深区间，建立了实测地层压力数据的扩充方法，实例计算中可将47点扩充至1522点，增幅31.38倍，显著增加了模型训练样本数量。

（3）利用Pearson相关系数优选了大钩载荷、泵压排量、层速度、自然伽马、声波时差等13个与Eaton指数相关性强的特征参数，用于挖掘钻测录震多源数据与Eaton指数之间的复杂非线性关系。可基于区块内已钻井的有限实测地层压力数据，实现全井段Eaton指数的精细预测，为新探区地层孔隙压力的准确预测提供了有效手段。算例中CNN-LSTM深度学习与Eaton法联合驱动的地层孔隙压力预测的平均误差为2.70%，而传统Eaton和LSTM与Eaton模型结合的相对误差分别为7.60%、5.12%。

参考文献：

［1］ 时梦璇，刘之的，杨学峰，等.地层孔隙压力地球物理测井预测技术综述及展望［J］.地球物理学进展，2020，35（5）：1845-1853.

SHI Mengxuan， LIU Zhidi， YANG Xuefeng， et al. Review and prospect prediction technology for formation pore pressure by geophysical welllogging［J］. Progress in Geophysics， 2020，35（5）：1845-1853.

［2］ AZADPOUR M， MANAMAN N S， KADKHODAIE-ILKHCHI A， et al. Pore pressure prediction and modeling using well-logging data in one of the gas fields in south of Iran［J］. Journal of Petroleum Science and Engineering， 2015，128：15-23.

［3］ 李磊，杨进，周波，等.渤海中深井复杂地层岩石特性及安全钻井周期研究［J］.中国海上油气，2022，34（3）：126-132.

LI Lei，YANG Jin，ZHOU Bo，et al.Rock characteristics and safe drilling cycle of complex formation in middle-deep wells in Bohai［J］.China Offshore Oil and Gas，2022，34（3）：126-132.

［4］ 杨振平，吴波，王勇.Eaton法预测M油田地层孔隙压力［J］.石油天然气学报，2012，34（9X）：181-182，187.

YANG Zhenping， WU Bo， WANG Yong. Application of Eaton method in predicting the formation pore pressure of M Oilfield［J］.Journal of Oil and Gas Technology， 2012，34（9X）：181-182，187.

［5］ 刘之的，夏宏泉，汤小燕.碳酸盐岩地层孔隙压力预测方法研究［J］.大庆石油地质与开发，2003，22（6）：8-10.

LIU Zhide， XIA Hongquan， TANG Xiaoyan. Study on predicting method of formation pore pressure for car-bonate rock［J］. Petroleum Geology & Oilfield Development in Daqing， 2003，22（6）：8-10.

［6］ 李中，刘和兴，李磊，等.基于改进的Bowers法预测南海陵水深水高温地层异常压力［J］.西安石油大学学报（自然科学版），2019，34（6）：60-66.

LI Zhong， LIU Hexing， LI Lei， et al. Prediction of abnormal pressure in Lingshui deep-water high temperature formation based on improved bowers method［J］. Journal of Xian Shiyou University（Natural Science Edition），2019，34（6）：60-66.

［7］ 田得强，李中，许亮斌，等.深水高温高压气井钻井循环温度压力耦合计算与分析［J］.中国海上油气，2022，34（5）：149-157.

TIAN Deqiang， LI Zhong， XU Liangbin， et al. Coupling calculation and analysis of circulating temperature pressure distribution in deepwater HTHP gas well drilling［J］.China Offshore Oil and Gas，2022，34（5）：149-157.

［8］ 张勇刚，王红平，王朝锋，等.地震资料在海域勘探初期地层压力预测中的应用［J］.石油地质与工程，2020，34（6）：8-12.

ZHANG Yonggang， WANG Hongping， WANG Chaofeng， et al. Application of seismic data in formation pressure prediction at the initial stage of offshore exploration［J］. Petroleum Geology and Engineering， 2020，34（6）：8-12.

［9］ 臧艷彬，王瑞和，王子振，等.利用Eaton法计算地层孔隙压力的不确定性分析［J］.西南石油大学学报（自然科学版），2012，34（4）：55-61.

ZANG Yanbin， WANG Ruihe， WANG Zizhen， et al. Evaluation of uncertainties for pore-pressure taking Eaton method as an example［J］. Journal of Southwest Petroleum University（Science & Technology Edition）， 2012，34（4）：55-61.

［10］ SHI X， CAI J， CHENG Y， et al. Estimating pore pressure in HPHT wells in Yinggehai Basin， China based on Hierarchical Eatons method［J］. Advanced Materials Research， 2012，347：3-9.

［11］ FARSI M， MOHAMADIAN N， GHORBANI H， et al.Predicting formation pore-pressure from well-log data with hybrid machine-learning optimization algorithms［J］. Natural Resources Research， 2021，30（5）：3455-3481.

［12］ 王磊，张辉，柯珂，等.基于遗传算法的深水无隔水管钻井液举升系统锚泊定位方案优化［J］.中国海上油气，2022，34（6）：142-148.

WANG Lei， ZHANG Hui， KE Ke， et al. Optimization of deepwater riser free drilling fluid lifting system mooring positioning scheme based on genetic algorithm［J］.China Offshore Oil and Gas，2022，34（6）：142-148.

［13］ 李春茂，徐云贵，刘浩杰，等.基于GBRT算法的地层孔隙压力预测研究［J］.中国石油和化工标准与质量，2022，42（5）：119-120.

LI Chunmao， XU Yungui， LIU Haojie， et al. Prediction of formation pore pressure based on GBRT algorithm［J］. China Petroleum and Chemical Standard and Quality， 2022，42（5）：119-120.

［14］ MATINKIA M， AMRAEINIYA A， BEHBOUD M M， et al. A novel approach to pore pressure modeling based on conventional well logs using convolutional neural network［J］.Journal of Petroleum Science and Engineering， 2022，211：110156.

［15］ 宋先知，姚学喆，李根生，等.基于LSTM-BP神經网络的地层孔隙压力计算方法［J］.石油科学通报，2022，7（1）：12-23.

SONG Xianzhi， YAO Xuezhe， LI Gensheng， et al. A novel method to calculate formation pressure based on the LSTM-BP neural network［J］.Petroleum Science Bulletin， 2022，7（1）：12-23.

［16］ EATON B A. The equation for geopressure prediction from well logs［R］. SPE 5544-MS， 1975.

［17］ 胜亚楠.钻井工程风险评估与控制技术研究［D］.青岛：中国石油大学（华东），2019.

SHENG Yanan. Research on risk assessment and control technology of drilling engineering［D］.Qingdao： China University of Petroleum （East China）， 2019.

［18］ 管志川，柯珂，路保平.压力不确定条件下套管层次及下深确定方法［J］.中国石油大学学报（自然科学版），2009，33（4）：71-75.

GUAN Zhichuan， KE Ke， LU Baoping. An approach to casing program design with formation pressure uncertainties［J］. Journal of China University of Petroleum（Edition of Natural Science）， 2009，33（4）：71-75.

［19］ 段中钰，吴俣，肖勇，等.基于CGAN与CNN-GRU组合模型的密度测井曲线重构方法［J］.地球物理学进展，2022，37（5）：1941-1945.

DUAN Zhongyu， WU Yu， XIAO Yong， et al. Density logging curve reconstruction method based on CGAN and CNN-GRU combined model［J］. Progress in Geophysics，2022，37（5）：1941-1945.

［20］ OGBAMIKHUMI A， EBENIRO J O. Reservoir properties estimation from 3D seismic data in the Alose field using artificial intelligence［J］. Journal of Petroleum Exploration and Production Technology， 2021，11（3）：1275-1287.

［21］ 黄家宸，张金川.机器学习预测油气产量现状［J］.油气藏评价与开发，2021，11（4）：613-620.

HUANG Jiachen， ZHANG Jinchuan. Overview of oil and gas production forecasting by machine learning［J］. Petroleum Reservoir Evaluation and Development， 2021，11（4）：613-620.

［22］ 许叶齐.页岩油异常地层压力预测方法的研究［D］.荆州：长江大学，2018.

XU Yeqi. Study on prediction method of abnormal stratigraphic pressure of shale oil［D］. Jingzhou： Yangtze University， 2018.

［23］ OKWUCHI I， NASSAR L， KARRAY F， et al. Deep learning ensemble based model for time series forecasting across multiple applications： IEEE International Conference on Systems， Man， and Cybernetics （SMC 2020）， 11-14 Oct. 2020， Toronto， ON， Canada［C］. Toronto： SMC， 2020.

［24］ HAN T， LIU C， WU L J， et al. An adaptive spatiotemporal feature learning approach for fault diagnosis in complex systems［J］. Mechanical Systems and Signal Processing， 2019，117：170-187.

［25］ 武中原，张欣，张春雷，等.基于LSTM循环神经网络的岩性识别方法［J］.岩性油气藏，2021，33（3）：120-128.

WU Zhongyuan， ZHANG Xin， ZHANG Chunlei， et al. Lithology identification based on LSTM recurrent neural network［J］. Lithologic Reservoirs， 2021，33（3）：120-128.

［26］ 韩晟，韩坚舟，赵璇，等.距离权重改进的Pearson相关系数及应用［J］.石油地球物理勘探，2019，54（6）：1363-1370.

HAN Sheng， HAN Jianzhou， ZHAO Xuan，et al. A Pearson correlation coefficient improved by spatial weight［J］. Oil Geophysical Prospecting， 2019，54（6）：1363-1370.

［27］ 刘瑞江，张业旺，闻崇炜，等.正交试验设计和分析方法研究［J］.实验技术与管理，2010，27（9）：52-55.

LIU Ruijiang， ZHANG Yewang， WEN Chongwei， et al. Study on the design and analysis methods of orthogonal experiment［J］. Experimental Technology and Management， 2010，27（9）：52-55.