多随机变量下的架空直立式码头桩基可靠度分析
2016-11-05郑涛何欢
郑涛+何欢

【摘 要】 为分析受多随机变量影响的架空直立式码头桩基可靠度,以重庆某架空直立式码头为例,利用有限元软件ANSYS建立架空直立式码头结构三维空间模型,将荷载、材料物理性能及计算模式作为随机变量,采用非线性加权响应面法拟合响应面函数,以替代极限状态功能函数,并应用当量正态化(JC)法求解桩基的可靠度指标。结果表明,前排桩的可靠度指标为8.897 5,与工程设计时考虑作用分项系数相吻合。
【关键词】 架空直立式码头;可靠度;桩基;响应面分析;撞击力
在三峡大坝蓄水后,库区水文条件发生了很大的变化,水位变幅大成为库区码头所需要解决的首要问题。架空直立式码头机械化程度高、吞吐量大,同时能很好地适应库区的大水位差特点,因此逐渐成为长江上游的主要码头结构形式。对于架空直立式码头结构的研究,庹莜葭等[1]建立平面有限元模型,将不同水位撞击力作为随机变量,对码头下部结构进行了可靠性分析,得到前排桩基及钢前撑在撞击力作为控制工况时的可靠指标。在实际工程中,码头处于空间受力状态,且其受力状态与计算模式、材料的物理特性等因素相关。因此,有必要建立空间模型,考虑多种随机变量,对架空直立式码头进行可靠度分析。
1 非线性加权响应面法
在通常情况下,架空直立式码头结构会受到多个方向荷载的同时作用,主要荷载包含船舶靠泊撞击力和系缆力、水流力、工艺机械荷载、堆载等,各荷载作用产生多个方向的轴向力、弯矩等力学相应量。由于该结构形式受力十分复杂,在进行可靠度分析时,功能函数一般为隐式。
笔者采用非线性加权响应面法,响应函数不含交叉项,能较好地反映出功能函数的非线性对可靠度的影响。同时,在选取试验点时,考虑试验点累计的情况。其函数形式如下:
3 工程实例
3.1 工程概况
笔者以重庆某架空直立式码头为例,码头排架间距为8 m,每榀排架设有4根钢筋砼嵌岩灌注桩,前排桩直径为2.2 m,后排桩直径为2 m,上部结构由现浇钢筋砼横梁、立柱,预制钢筋砼纵梁及叠合面板组成。
3.2 有限元模型及可靠度分析
有限元模型及可靠指标求解的主要步骤为:
(1)利用有限元软件ANSYS建立码头某一结构段的有限元空间模型,并进行运算,然后提取结果。
(2)通过ANSYS-PDS模块输入随机变量参数,将码头结构的几何尺寸、水流力视作常量,将堆载、撞击力、系缆力、混凝土和钢材的物理特性、计算模式作为随机变量,按照指定的结构响应量进行输出,通过Bucher设计抽样拟合响应面函数,采用JC法进行可靠度指标求解。
(3)利用式(6)得到新的抽样中心点,然后再次通过ANSYS-PDS模块进行拟合得到相应的响应面函数,并重复步骤(2),直至可靠度指标满足精度要求时停止迭代,输出结果为最终的可靠度指标。
以前排桩强度可靠度指标为例进行分析,模型采用SHELL 63壳单元模拟码头平台面板,BEAM 189梁单元模拟其他构件。边界条件为在桩基的假想嵌固点处约束6个自由度,在结构分段处采用铰接形式约束梁端自由(见图2)。
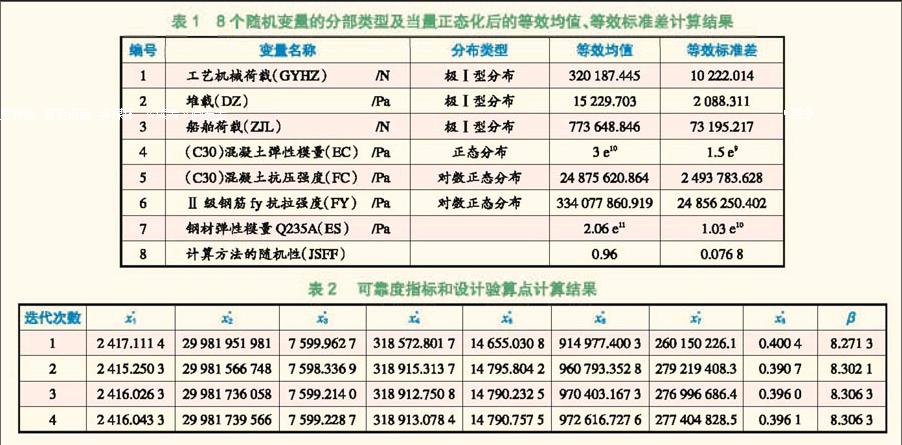
计算8个随机变量的分布类型及当量正态化后的等效均值、等效标准差(见表1),并按照Bucher设计进行11次抽样,首次抽样的中心点为各随机变量的均值点, f 取2,拟合得到样本点。根据非线性加权响应面法的基本思路,按照圆形截面偏心受压构件正截面承载力计算方法求得的前排桩截面抗力值作为抗力响应量ri,根据gi= ri si (gi 为实验响应量,si 为效应响应量,i=1,2,…,n)即可得响应面函数的响应量列阵y=(g1,g2,…,gn)以及权重wi (i=1,2,…,n)。
利用最小二乘法,对样本点和对应的响应量进行回归分析,对响应面函数中的系数进行最小二乘估计,拟合得到响应面函数,再对求得的响应面函数按照求解可靠度指标的过程,得到初次迭代可靠度指标及其验算点(见表2)。
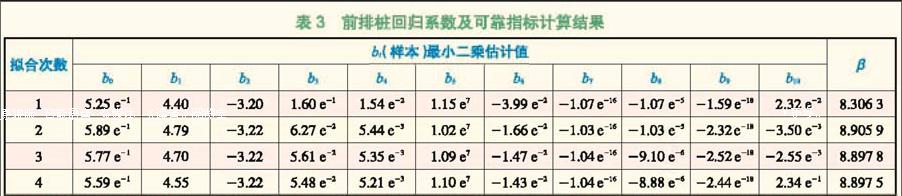
从表2可以看出,经过4次迭代,初次拟合的响应面方程的 收敛于。将最后一次迭代时各个随机变量相对应的验算点值重新带入有限元模型中进行运算(即有限元重分析),并将求得该验算点对应的响应量,按照式(6)可得到下一次抽样中心点。如此反复进行抽样、回归分析、可靠指标求解、插值等几个主要步骤,直到满足 (i + 1) (i)< 时,得到的 值可作为最终求得的桩基可靠度指标(见表3)。
4 结 语
根据以上的论述和分析,可以得出以下结论:
(1)架空直立式码头是受力较为复杂的结构,在进行可靠度分析时其功能函数无法显示表达。利用有限元软件ANSYS建立结构的空间模型,并运用ANSYS-PDS模块,可以考虑多种随机变量。采用非线性加权响应面法可以拟合出替代功能函数的响应面函数,结合JC法求解可靠度指标,经过4次迭代后便能够较快地收敛,求得验算点和可靠度指标。
(2)各荷载均采用标准值进行计算。按照正截面承载能力计算时,前排桩的可靠度指标为,远大于港口工程设计的可靠度指标最大值4,这与在工程设计时考虑作用分项系数相吻合。
参考文献:
[1] 庹莜葭,王多银,李泉源,等.内河架空直立式码头下部结构可靠度分析[J].中国港湾建设,2014(12):1-5.
[2] 赵国藩.工程结构可靠性理论与应用[M].大连:大连理工大学出版社,1996:46-50.
表3 前排桩回归系数及可靠指标计算结果
