逆流条件下基于能量守恒的Taylor泡运移速度预测模型

娄文强 王金堂 贺艳祥 张党生 孙小辉 孙宝江 王志远

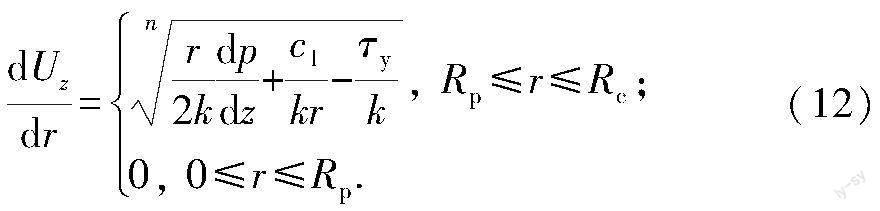
摘要：在逆流條件下分析Taylor气泡运移行为，考虑流体的特征本构方程提出管流流场及Taylor气泡周围速度场计算方法，基于速度场模型建立气泡各阻力的能量耗散模型。基于能量守恒分析提出统一的适用于不同流变类型的Taylor泡上升速度预测模型（模型T），探究逆流条件下Taylor泡运移规律。结果表明：与公开试验数据对比，模型T对逆流条件下Taylor泡运移速度转折点的预测误差小于7.35%；随气泡体积增加，鼻端区域和尾流区域的能量耗散比例降低，液膜区的能量耗散比例增加；随气泡体积增加，屈服应力、惯性力和表面张力做功占比降低，黏性耗散占比增加；制约气泡上升速度增加的原因是气泡浮力做功增加的正功值被液膜区增加的能量耗散相抵消。

关键词：逆流流动； Taylor泡； 速度预测模型； 速度场； 能量转化

中图分类号：O 359.1 文献标志码：A

引用格式：娄文强，王金堂，贺艳祥，等.逆流条件下基于能量守恒的Taylor泡运移速度预测模型［J］.中国石油大学学报（自然科学版），2023，47（6）：60-71.

LOU Wenqiang， WANG Jintang， HE Yanxiang， et al. Taylor bubble migration velocity prediction model based on energy conservation under countercurrent condition［J］.Journal of China University of Petroleum（Edition of Natural Science），2023，47（6）：60-71.

Taylor bubble migration velocity prediction model based on

energy conservation under countercurrent condition

LOU Wenqiang1， WANG Jintang1， HE Yanxiang2， ZHANG Dangsheng3，

SUN Xiaohui1， SUN Baojiang 1，4， WANG Zhiyuan1，4

（1.School of Petroleum Engineering in China University of Petroleum （East China）， Qingdao 266580， China;

2.PetroChina Coalbed Methane Company Limited， Beijing 100028， China;

3.Downhole Operation Branch of CNPC Bohai Drilling Engineering Company Limited， Cangzhou 062552， China;

4.Key Laboratory of Unconventional Oil & Gas Development （China University of Petroleum （East China）），

Ministry of Education， Qingdao 266580， China）

Abstract： Based on the analysis of Taylor bubble migration behavior under countercurrent condition and considering the characteristic constitutive equation of fluid， the calculation method of pipe flow field and velocity field around Taylor bubble was proposed， and the energy dissipation model of bubble resistance based on the velocity field model was established. On the bases of the energy conservation analysis， a unified Taylor bubble rising velocity prediction model （Model T） suitable for different rheological types was put forward to explore the law of Taylor bubble migration under countercurrent conditions. The results show that compared with the public experimental data， the prediction error of model T for the turning point of Taylor bubble migration velocity under countercurrent conditions is less than 7.35%. With the increase of bubble volume， the energy dissipation ratio of nose region and wake region decreases， and the energy dissipation ratio of the liquid film region increases. With the increase of bubble volume， the work proportion of yield stress， inertial force and surface tension decreases， and the proportion of viscous dissipation increases. The reason for restricting the increase of bubble rising speed is that the positive work value of bubble buoyancy is offset by the increased energy dissipation in the liquid film area.

Keywords： countercurrent flow; Taylor bubble; speed prediction model; velocity field; energy conversion

多相反应器技术可以有效地解决化学多相反应效率问题，为化学反应过程提供了有效的传质和传热性能，广泛应用于气体吸附、催化加氢、生化转化和直接氟化［1-2］。气液反应器的传质和反应性能在很大程度上取决于反应器内气液两相流的流体动力学［3-4］。气液反应最有价值的流型是段塞流［5］，段塞流的基本单元结构由长气泡和管内液体段塞组成，气泡在管内呈长子弹的形状，气体几乎占据了整个管道截面，液体以液膜的形式在气泡和管壁之间流动［6-7］。微反应器中控制流型为层流流型，因此多相反应器中的流动具有气液接触面高、压降低的优点，改善了气液两相传质过程，在各种化学反应过程中有着广泛的应用［8-9］。微通道内的气液流体力学是影响段塞流质量和传热过程的关键因素［10］。因此分析微反应器内Taylor泡的运移速度和流场特性是解决微反应器内传质和传热效率问题的关键。Taylor泡在微通道中的速度、膜厚、流场和停留时间对气液传质系数和反应效率有很大影响［11］。气液两相并流和逆流具有完全不同的传质系数，影响传质系数的关键因素是管道中气泡的速度差［5］。当气液两相处于逆流状态时，Taylor泡的速度明显降低。增加气液相的接触时间可以提高反应效率。笔者结合流体的流变特性建立气泡周围流场预测模型，同时基于能量守恒模型建立适用于全部流体的统一预测模型（简称模型T）并进行验证，采用能量分析模型对Taylor气泡上升过程中的影响因素进行分析。

1 速度场分析

圆管内流体平稳流动时，流体剪切变形产生特定的能量损失，当Taylor气泡与流体逆向运动时，将打破圆管内原有的平稳流动状态。气泡周围流体受气泡的扰动作用形成新的绕流流场，流场分布是揭示能量转移过程的基础。基于流体的流变响应特征可以将流体分为屈服性流体和黏性流体，本质区别在于是否具有屈服应力，本文中分别采用幂律和赫巴模式描述黏性流体和屈服性流体，建立相应的流场预测模型。

1.1 管流流场

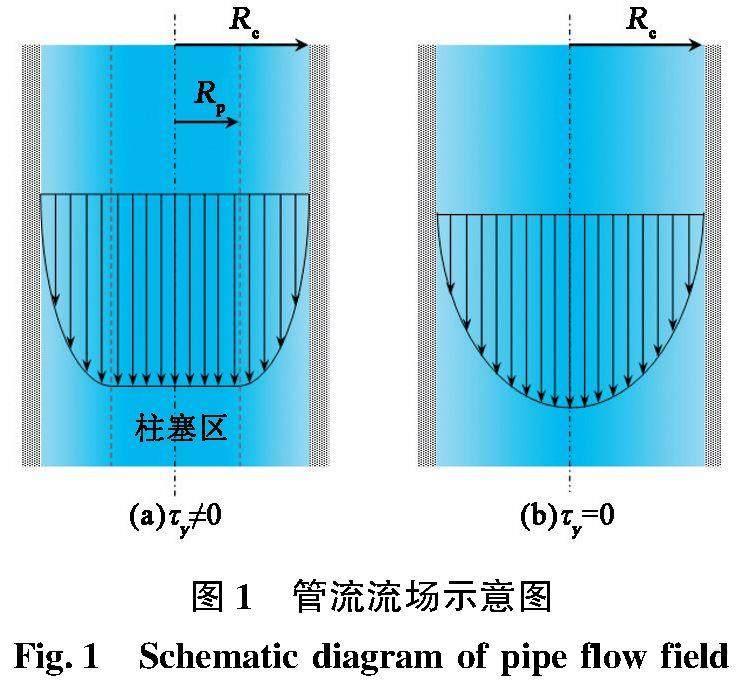
图1为圆管内屈服应力流体和黏性流体的流动示意图。流体不具有屈服应力时，作用在流体上的任何微小剪切应力即可使流体产生连续变形，当流体具有屈服应力值后，只有剪切应力超过流体特有的屈服应力之后才会发生流动。屈服应力流体在圆管内流动时存在一个应力小于屈服应力的流动区域，称之为柱塞区。由于流体性质差异引起管内速度场分布不同，圆管内流体剪切变形产生的能量转移过程有一定的差异，因此需要揭示圆管内不同流体的流场分布。

圆管内的单相流动研究相对成熟，考虑不可压缩流体在静止圆管作稳态、层流流动，在轴向上施加一个恒定的压力梯度dp/dz，则流动控制方程［12］为

式中，ρl为液相密度，kg/m3；U为流体质点的速度矢量；p为压力，Pa；τ流体的偏应力张量。在柱坐标系（r，θ，z）下速度矢量U满足：

U=Urer+Uzez+Uθeθ.（3）

式中，er、ez、eθ为柱坐标系下的方向向量；Ur、Uz、Uθ为柱坐标系下径向、垂向、周向的速度分量，m/s。

根据圆管流动的轴对称性，管内流体质点的唯一非零速度分量为Uz，因此速度分量Ur和Uθ自然满足连续性方程和动量方程。基于此对方程（3）进行简化，得到管流轴向动量方程：

式中，τz为偏应力张量τ的唯一非零分量；dp/dz为流体的压力梯度，Pa/m；r为半径，m。对方程（4）进行积分求解，可得到圆管内流体流动的应力方程：

式中，C1为常系数。联立流体本构方程与应力方程（5）可求解管内径向方向的速度分布，因此在求解速度分布时需要针对特定的流体建立模型。

（1）黏性流体。黏性流体受应力作用即会发生剪切变形，且剪切流动满足流体本构方程。基于流体速度梯度可以表征黏性流体流动时的应力方程：

式中，k为稠度系数，Pa·sn；n为幂律指数，无量纲。管壁处边界条件为无滑移边界，因此流体质点在管壁（r=Rc）处速度为零。在管中心轴线位置处速度梯度发生反转，而流体的应力具有连续性，因此在管中心轴线位置处流体的切应力为零。黏性流体在圆管中流动时的边界条件为

Uzr=Rc=0，（7）

τzr=0=0.（8）

联立应力方程（5）和（6）可得到速度梯度微分方程，将边界条件（7）和（8）代入速度梯度微分方程中求解積分常数，得到圆管中黏性流体速度场分布方程：

求解速度场模型（9）时仍存在未知量dp/dz，需要补充新的方程以使方程组闭合。圆管内流体流动时满足质量守恒方程，假设液体为不可压缩流体，管内流体的连续性方程为

（2）屈服应力流体。圆管内流体发生剪切流动时满足流体的本构方程，因此屈服应力流体的应力方程可由流体的速度梯度表征。

式中，τy为屈服应力，Pa。屈服应力流体在圆管中流动时存在柱塞区（r

式中，Rp为屈服界面半径，m；Rc为管径，m。屈服应力流体的流动边界在管壁处与黏性流体流动相同，由于柱塞区的产生，屈服应力流体流动产生了新的流动边界，柱塞区边界Rp处，流体的速度梯度为零，切应力等于流体的屈服应力。该流动边界方程为

τzr=Rp=τy.（13）

将边界方程带入应力方程（11）和速度场方程（12）中，得到仅含有未知数Rp的速度场模型。

速度场方程（14）中仍存在柱塞边界Rp未知，为得到准确的速度场分布函数，利用连续性方程求解柱塞边界Rp：

式中，Ql为液相流量，m3/s。

1.2 气泡周围流场分布

Taylor气泡达到稳定上升状态之后气泡形状相对稳定，基于已有试验结果，假设逆流条件下Taylor气泡形状分为3个区域［13］（几何模型见图2）：①气泡前端的形状是半径为Rb的半球体，并伴随一个半径为Rn的球状扰动区域（图2（b））；②气泡鼻端以下液膜厚度相同，气泡形状为一段被液膜包围的圆柱体，圆柱体半径为Rb，长度为Lf；③Taylor气泡尾部扁平，并伴随一个长度为Lw的扰动扰动尾流区（图2（d））。

液相逆流流动状态下，Taylor气泡的出现会改变圆管内的流动状态（图1中的流动状态）。当原有的流场分布发生改变之后，流体剪切变形产生的能量耗散分布以及数值都将随之改变。因此，揭示逆流条件下气泡动力学问题的关键是分析Taylor气泡周围流场分布。

1.2.1 液膜区速度场

逆流条件下Taylor气泡的形状变化微弱且具有轴对称型，气泡周围的液膜厚度相对稳定，且液膜区的流体流动属于层流流动。因此逆流条件下气泡周围的液膜区的流动与同心环空内单相流动相似，液膜内流体的流动情况如图3所示。液膜内流体的流动控制方程与圆管内流体的控制方程相同，流体应力方程化简之后与方程（5）相同。

根据流体的流变类型可将液膜内的流动分为2种类型：①无柱塞区的剪切流动（黏性流体），如图3（a）所示；②存在柱塞区的剪切流动（屈服应力流体），如图3（b）所示。由于气液界面边界不同于常规同心环空流动，因此需要根据流动工况分别建立速度场计算模型。

（1）黏性流体。当Taylor气泡周围的流体为黏性流体时，流动类型如图3（a）所示。液膜流动存在2个边界条件：气泡壁面边界B1为滑移边界，气液界面位置处的切应力为零；圆管内壁面B2为无滑移边界，与管流流动边界相同。

τrr=Rb=0.（16）

联立应力方程（5）和（6）得到液膜内速度场方程的通解，利用边界条件推导得到黏性流体液膜速度场方程：

（2）屈服应力流体。屈服应力流体的液膜流动如图3（b）所示，与黏性流体液膜流动相比，新增了屈服界面边界：

τrr=Rx=τy.（18）

联立应力方程和边界条件，得到屈服应力流体液膜的速度场模型：

式中，Rx为液膜屈服界面，m。速度场方程（17）和（19）中仍含有未知数dp/dz和Rx，需要利用管内流动的连续性方程将方程组闭合。通过连续性方程对速度场模型中的未知数进行校验，获取相应流变模式下的液膜速度场分布：

1.2.2 鼻端区速度场

当Taylor泡与液相逆向流动时，气泡鼻端将干扰流体质点的运动状态，打破原有的速度场分布。靠近气泡鼻尖的位置，气泡对流体的影响作用较强；远离气泡的位置，气泡对液体的干扰能力降低，流体质点的速度矢量将保持原有的运动状态。在气泡鼻端存在一个边界，在边界以内流体质点受气泡的扰动影响，在边界以外流体保持原有的状态，称该边界为气泡扰动边界，如图2（b）中所示的边界（r=Rn）。诸多研究结果表明，流体黏度对气泡扰动区域的大小影响较大，随黏度增加气泡扰动区域缩小，Araújo等［14］提出适用于黏性流体中Taylor泡鼻端扰动边界计算模型：

式中，Rn为扰动边界，m；Nf为无量纲逆黏度系数，Nf=ρ（gD3）0.5/μ。

Taylor气泡具有球状鼻端，周围流体流动近似为理想的绕球体流动。在理想绕球体流动中，利用势流理论可得到球体周围流体质点的周向速度分量与径向速度分量的关系：

假设气泡鼻端的绕流始终满足式（22）和（23），并基于此建立绕流速度场模型［15］。

与无限大区域中绕球流动的区别是Taylor气泡前端的扰动区域边界由管壁和扰动边界组成。扰动区域内流体质点的速度矢量不仅需要满足绕流速度矢量关系，仍需要满足质量守恒方程。在以鼻端球心为坐标原点的球坐标系下，建立沿气泡周向的连续性方程：

式中，Qθ为周向方向的液体通量，m3/s。由液膜区的速度场计算模型和速度矢量关系（22）联立求取。受流体流变性的影响，黏性流体和屈服应力流体的周向液体通量为

根据流体的流变类型，结合薄膜区速度场计算方法、气泡鼻端流体质点速度矢量关系、连续性方程及液体通量计算模型可求解出气泡鼻端扰动区域内流场分布及流体质点的速度分量Uθ、Ur。

1.2.3 尾流区域速度场

液膜内的流体流经Taylor泡扁平的尾部时，由于流动通道突然增加，来自液膜的流体开始做减速运动。流动通道的改变使气泡尾部的流体产生径向动量扩散和轴向动量扩散，两个方向动量的扩散竞争使气泡尾部形成一个循环的涡流。尾流区内流体动量的径向和轴向扩散强度决定了循环涡流的长度Lw，本文中采用Sousa等［16］提出的尾流计算模型：

Lw/D=0.2+1.14×10-3Nf， Nf<800.（27）

尾流内存在强烈的循环涡环，涡环的上升速度与气泡上升速度相当。气泡尾部涡环的速度场难以解析描述，在进行速度场分析时，假设气泡尾流区内速度梯度近似为气泡速度与尾流长度的比值［13］，即

dUw/dr=Ub/Lw.（28）

2 气泡运移速度预测模型建立

圆管内流体在压力驱动下发生流动，流体的黏性作用使流体在流动时产生速度梯度，即发生剪切变形。流体发生剪切变形的过程伴随着能量的转化，将流体具有的机械能转化为内能，且这种转化不可逆。流体产生剪切变形及能量转化的过程如图4所示。气泡在运动的过程伴随着两个能量耗散的过程：一是流体在圆管内流动时，流体剪切变形产生能量耗散，消耗流体具有的壓能;二是Taylor气泡改变逆流原有的流场分布，产生了附加的能量耗散，消耗气泡浮力做功。气泡在逆流条件下运动时满足能量守恒定律，即气泡浮力做功与气泡周围流体产生的附加能量耗散平衡，维持稳定的上升速度。基于逆流条件下的管流速度场及气泡周围流体的流场分布建立能量计算模型，结合能量守恒模型，建立逆流条件下的气泡上升速度预测模型。

2.1 能量耗散模型

2.1.1 管流能量耗散

圆管内流体在压差作用下发生剪切变形，形成稳定的流动，流体受黏性力和屈服应力作用，在流体发生稳定剪切变形的过程中伴随着黏性耗散和屈服耗散：

Wp=Wvp+Wyp.（29）

式中，Wp为管流耗散，W；Wyp为屈服应力做功值，W；Wvp为黏性力做功值，W。在发生剪切变形的区域内流体流动产生的黏性耗散与kγn+1成正比关系，结合管内流场分布函数，可得到流体黏性耗散的计算模型［17-18］：

式中，H为管道长度，m。圆管内剪切区域流体发生剪切变形时，屈服应力引起的能量耗散与与τyγ成正比关系，结合圆管内流体速度场的分布函数，可得到流体屈服应力能量耗散的计算模型：

2.1.2 气泡周围流体能量耗散

Taylor气泡在流体中运移时受重力、浮力、惯性力、黏性力、表面张力和屈服应力，除浮力外其他力均作为阻力，在气泡上升过程中做负功，消耗气泡浮力做功产生的能量。气泡鼻端扰动边界及尾流边界以外流体保持原有状态，流体的能量转化主要发生在扰动边界和尾流边界之间的剪切区域。求解单个Taylor气泡阻力能量耗散时，需要针对各阻力做功方式及其特定区域进行分析。

（1）黏性力做功。气泡运移时扰动周围的流体，使流体的流动限制在气泡的鼻端扰动区，薄膜区和尾流区，在这3个区域内流体发生剪切变形，黏性力做功消耗流体具有的机械能，致使流体的内能增加。因此黏性力做功主要包括鼻端区域流体的黏性耗散，液膜区流体的黏性耗散和尾流区流体的黏性耗散。Taylor气泡上升过程中的黏性力做功可分为3个部分，总黏性耗散为

Wv=Wvn+Wvf+Wvw.（32）

式中，Wv为黏性耗散，W；Wvn、Wvf、Wvw分别为气泡鼻端区域、液膜区和尾流区的黏性力做功值，W。黏性力做功与相应区域内的速度梯度相关，结合每个区域内流体速度场计算模型可分别计算出对应区域的黏性耗散值。气泡鼻端区域的边界由扰动边界和管壁组成，该区域的黏性耗散需要针对边界建立分段函数进行计算：

液膜区的黏性耗散计算方法为

尾流区流体黏性耗散计算方法为

（2）屈服应力做功。当流体具有屈服应力之后，在气泡上升过程中屈服应力做功与黏性力做功相似，包括气泡鼻端区域的屈服耗散，液膜区流体的屈服耗散和尾流流体的屈服耗散，总屈服耗散方程为

Wy=Wyn+Wyf+Wyw.（36）

式中，Wyn、Wyf、Wyw分别为气泡鼻端区域、液膜区和尾流区的屈服应力做功值，W。在发生剪切流动的区域内，屈服应力做功与流体的速度梯度正相关，基于Taylor气泡周围流场模型，可以求解出每个区域内对应的屈服应力做功值。根据气泡鼻端区域的特征边界建立屈服耗散的分段计算函数：

液膜区流体屈服应力做功计算方法为

尾流区流体屈服应力做功计算方法为

（3）惯性力做功。Taylor气泡上升过程中惯性力的影响主要体现在气泡的前端与后端，因此惯性力做功主要发生在气泡的鼻端扰动区和气泡的尾流区。气泡上升过程中惯性力总做功包括鼻端惯性耗散Win和尾流惯性耗散Wiw，基于此建立惯性力总做功值的计算公式［17］为

Wi=Win+Wiw.（40）

慣性力做功不仅由鼻端扰动区和尾流区流体质点的速度决定，还与气泡上升速度的平方正相关。结合气泡前端区域内流场分布关系以及鼻端的特征扰动边界可建立鼻端区惯性力做功计算方法：

结合尾流区的速度场分布以及尾流边界建立尾流区的惯性耗散计算模型：

（4）表面张力做功。Taylor气泡圆柱段具有对称性，表面张力的合力为零，在气泡上升过程中不做功。而气泡鼻端与气泡尾端形状不对称，在气泡运动方向上表面张力合力不为零，在气泡运移过程中做功，表面张力做功的计算公式［13］为

式中，Ws为表面张力做功，W；σ为表面张力，N/m。

2.2 气泡上升速度预测模型

单个Taylor气泡在静止流体中运移时，浮力作为驱动气泡运动的唯一动力，在气泡运动过程中做正功，而其他力作为气泡上升的阻力，在气泡运动过程中做负功。在气泡达到稳定状态之后，动力做功与阻力做功平衡，满足能量守恒定律［19］。气泡运移过程中的能量守恒方程表示为

Wb=Wy+Wv+Wi+Ws-Wp.（44）

式中，Wb为气泡浮力做功值，W；Wy为屈服应力做功值，W；Wv为黏性力做功值，W；Wi为惯性力做功值，W；Ws为表面张力做功值，W；Wp为管流流动的固有能量耗散，W。

浮力做功与气泡体积和气泡上升速度正相关，计算方程为

Wb=（ρ1-ρg）gVbUb.（45）

式中，ρl和ρg分别为液体密度和气体密度，kg/m3；Vb为气泡体积，m3；g为重力加速度，m/s2；Ub为气泡上升速度，m/s。

基于能量守恒求解逆流条件下的Taylor气泡上升速度时，首先需要分析逆流条件下圆管内的流场及坐标系转化之后的气泡周围速度场分布，利用速度场计算结果分别求解逆流流体的能量耗散及气泡周围流体的能量耗散，将能量耗散计算结果带入能量守恒方程中可求解得到Taylor气泡的上升速度。以管流速度场和气泡周围速度场为基础的能量守恒模型中存在唯一的未知变量Ub，通过迭代计算得到气泡的上升速度，速度预测模型为

ρ1gUbVb=Wyf+Wvf+Wyn+Wvn+Win+Wvw+Wyw+Wiw+Ws-Wvp-Wyp=f（Rb，Ltb，Lw，Rsc，Ub，Ur，Uθ，Uz，Uw，σ，Rc，τy，k，n，ρ1，Q1）.（46）

3 模型验证及结果分析

3.1 速度场模型验证

气泡周围流体流动状态不仅影响气泡的上升速度，对气泡周围流体的传热传质等行为都具有一定的影响。气泡在流体中运移时取代了前端的流体，对流体产生一个局限的扰动，因此在圆管内形成一个局部剪切区域。为验证本研究中流场模型的准确性，使用Sousa等［16］的试验数据对模型结果进行对比分析，将其流变参数和气泡尺寸数据代入统一模型中进行模拟，输出Taylor泡周围的流场模拟结果，图5给出模型计算结果与试验结果的对比。可以看出，模型T的数值计算结果与试验结果具有较高的吻合度。

图6（a）为模型T计算的气泡鼻端流场分布矢量图。试验流变参数对应Sousa等［15］文中质量分数为0.8%的cmc（临界胶束浓度，记为w（cmc））溶液。由图中信息可知，在靠近气液界面的位置，速度矢量表现出强烈的径向分量，远离气泡的位置由于扰动强度降低，流体质点的速度矢量迅速衰减，形成稳定的扰动边界。图6（b）为图（a）中（z/Rc=0.91、z/Rc=160、z/Rc=1.84）的流体质点轴向速度分布。由3个位置处的速度分布可以看出，受气泡形状的影响，管中心位置处流体质点的速度最高。沿管径方向发展，流体质点速度迅速降低，并在扰动边界和管壁处降低为零。远离气液界面的截面处（z/Rc=1.84），扰动边界以内的流体受气泡影响，扰动边界以外流体保持原有的状态。靠近气泡鼻端的位置（z/Rc=0.91），扰动强度高，流体质点具有较高的速度。但在该位置处管壁的作用明显，满足连续性方程的条件下，流体出现负方向的速度。同时对比3个位置处的速度分布发现，气泡的扰动强度并不是线性衰减，距离气泡位置越远，衰减越快。气泡扰动强度是受流体流变参数影响的，随着流体非牛顿性质的增强，流体流动的非线性增强，扰动强度发生非线性衰减。

3.2 运移速度验证

利用气泡的尺寸参数、流体的流变参数、管径数据、液相流量参数，选取对应流变模式下的速度场预测模型，将速度场计算结果代入能量守恒方程中，通过迭代计算可得到Taylor气泡的上升速度。在进行模型验证时需要对Taylor气泡上升过程中的液膜厚度进行表征，以确定气泡的形状尺寸。选用Azevedo等［20］基于试验获取的液膜厚度（δ）预测公式：

δ=（-4.19×10-2lnNf+4.25×10-1）Rc.（47）

Benattalah等［21］对直径D为10.2 mm圆管内逆流条件下Taylor气泡运移行为开展研究，数据涵盖气泡的静止状态、上升和下降状态，能够较为全面地反映逆流条件下的Taylor气泡运移行为。其中未明确给出逆流条件下运移气泡的尺寸数据，利用方程（47）计算的液膜厚度，其气泡长度的范围为6D～50D，以此数据为基础进行模拟计算，模型计算结果与试验数据对比见图7。可以看出，模型T计算结果与其试验数据具有较高的吻合度，气泡长度在发生大范围变化时，Taylor气泡的上升速度变化微弱。

Fershtman等［22］分析逆流条件下Taylor泡的运移行为，通过提取其文章中的图像信息，利用模型T对不同逆流流速条件下的气泡上升速度进行预测，图8为对比结果。可以看出，在气泡由向上运移转移到向下运移的过程中，模型T都显示良好的预测精度，速度转折点的预测误差为7.35%。

Griffith等［23］、Nicklin等［24］、Martin［25］等开展气液逆流试验，试验结果只涵盖了气泡上升速度为正的范围，结果见图9。选取气泡长度为10D，利用液膜经验公式计算气泡的尺寸参数，带入模型T得到理论计算结果。由图中数据对比分析可知，模型T与文献试验数据具有较高的吻合度，速度转折点的预测误差为3.75%。

3.3 气泡上升速度影响因素

3.3.1 不同区域的能量耗散分布

基于速度场分析，可以揭示不同区域内流体能量耗散的分布规律。针对不同流变类型流体中Taylor泡鼻端區域内的能量耗散情况进行模拟，结果见图10。可以看出，Taylor气泡在流体中运移时，气液界面处流体产生的能量耗散值较低，主要是由于零剪切应力边界引起的低剪切速率导致的。而管壁附近流体产生的能量耗散较高，影响着整个鼻端区域的能量分布。相同幂律指数n和稠度系数k条件下，屈服应力流体的能量耗散明显高于幂率流体。屈服应力的出现改变了气泡周围的流场分布，同时作为阻力产生了相应的能量耗散。因此当流体具有屈服应力之后，气体运移产生了附加阻力，气泡的上升速度相应地被降低。

气泡鼻端的能量分布显示，由气泡前端扰动边界向下，随流动通道发生改变，能量耗散迅速增加，在气泡与管壁之间的液膜区是能量耗散的主要发生区。图11为气泡在幂率流体（k=2.4 Pa·sn， n=0.4）和赫巴流体（τy=1.5 Pa， k=2.4 Pa·sn， n=0.4）中运移时液膜内速度场及能量耗散分布情况。与鼻端气泡能量分布相同的是，能量耗散极大值出现在管壁处，由管壁向内随速度梯度的降低，能量耗散逐渐降低，在气泡壁面处出现极小值。流体的屈服应力使液膜内流体流动产生了一个柱塞区，在柱塞区内流体平稳流动不产生能量耗散。图中的能量分布显示，屈服应力流体中高能量耗散区域的范围明显大于幂率流体中的范围。即屈服应力的出现将会增加液膜区的能量耗散，最终表现为Taylor气泡的上升速度降低。

由模拟结果可知，气泡周围流体的黏度增加，高能量耗散区域的范围增加，总能量耗散值高，相同体积条件下的气泡上升速度降低。流体具有屈服应力后，气泡各个区域内的流体流动将会产生屈服耗散，导致气泡阻力做功总值增加，降低气泡上升的速度。因此流体的屈服应力对气泡运移行为的影响不容忽视，提出的统一模型能有效解决屈服应力流体中气体运移速度预测准确度低的难题。

3.3.2 能量耗散权重

Taylor气泡上升过程中扰动周围流体，流体的剪切流动消耗浮力所做的功，而不同区域内具有不同的流动特征，对浮力做功产生的耗散作用也不同。因此基于Taylor气泡形状产生的扰动特征对气泡上升速度产生了不同的影响，气泡周围区域内流体做功的权重分析见图12。可以看出，鼻端区域和尾流区域的能量耗散占比随气泡长度增加而降低，液膜区的能量耗散随气泡长度增而增加。在低气泡长度条件下鼻端区域为能量耗散的主要区域，高气泡长度条件下液膜区为主要能量耗散区域。气泡尾流区域的能量耗散在气泡长度变化过程中一直保持较低的占比，对气泡的影响相对较小。这种能量分布产生的原因主要是气泡鼻端和尾流区的形状不随气泡体积的增加而产生较大的变化，同时气泡的上升速度在气泡体积增加的过程中增加也不明显，最终导致鼻端区域和尾流区域内的能量耗散值变化较小。而液膜区的长度随气泡体积增加迅速增加，产生的黏性耗散和屈服耗散也迅速增加，成为影响Taylor气泡速度上升的主导因素。

气泡上升过程中受流体黏性力、惯性力、屈服应力和气泡表面张力的作用，每种作用力对气泡的上升过程产生不同的影响效果，它们的相对值对气泡上升速度起着决定性作用。基于Taylor气泡周围速度场分析，利用能量计算方程可求解出气泡上升过程中的各力做功情况，图13为屈服应力、黏性力、惯性力、表面张力做功占浮力做功的比值。可以看出，随气泡长度增加黏性耗散对浮力做功的消耗作用逐渐增加，成为影响气泡上升的主导因素，其他力做功所占比例均降低。

Taylor气泡体积增加过程中，液膜厚度变化十分微弱，气泡的鼻端和尾部形状相对稳定，气泡形状特征中发生明显改变的只有气泡的长度。诸多试验结果表明，同一圆管内Taylor气泡的终速度相对平稳，不再是气泡体积的单调函数。流体产生的惯性能量耗散主要发生在气泡的鼻端和尾流区，在稳定的气泡形状特征以及上升终速度条件下，气泡鼻端和尾流区内的速度场分布变化较小。因此惯性力做功值相对稳定，而气泡的浮力做功与气泡体积呈正比例关系，因此惯性项产生的耗散比例在气泡体积增加过程中表现出下降趋势。表面张力做功与气泡的上升速度呈正比力关系，当气泡上升速度稳定时，表面张力做功值保持不变，消耗能量的比例随气泡体积增加而降低。由于液膜厚度和气泡的上升速度变化较小，液膜内的速度场表现出穩定的状态，气泡长度增加时液膜内产生的能量耗散增加。由此可知，气泡体积增加，浮力做功值增加，液膜区产生的能量耗散也增加。由于气泡体积增加产生的正功增加值被液膜区增加的能量耗散消耗，气泡表现出上升速度稳定。液膜内流体产生的能量耗散主要包括屈服耗散和黏性耗散，气泡长度增加过程中这两者均表现为做功值增加的状态。而两者做功所占比例的变化趋势主要取决于屈服应力和黏性力的相对值，图13表明，该流变参数条件下黏性力做功值远高于屈服应力，因此黏性耗散占比表现为增加状态，而屈服应力表现出缓慢的降低趋势。

由图13可知，表面张力对浮力做功产生的耗散比例低于0.2%，因此当气泡形状相对稳定时，表面张力对气泡上升速度的影响十分微弱，可以忽略［26-27］。另外屈服应力对气泡浮力做功的耗散比例接近18%，其对气泡上升速度产生不可忽略的影响，对气泡上升速度进行预测时必须考虑流体的屈服应力。

4 结 论

（1）考虑不同流体特有的流变特性，提出不同流体中Taylor气泡周围流场计算方法，结合速度场模型，推导Taylor气泡运移过程中周围流体的能量耗散模型。基于气泡运移过程的能量守恒定律，建立逆流条件下Taylor气泡上升速度预测模型。提出的统一模型（模型T）解决了逆流条件下牛顿流体、幂律流体、屈服应力流体中Taylor气泡上升速度的预测。

（2）模型T能够较准确预测气泡运移过程中的速度场分布，能够准确预测不同流速下的Taylor泡运移速度，对速度转折点的预测精度小于7.35%。

（3）随Taylor气泡体积增加，液膜区产生的能量耗散成为主导气泡上升速度关键，鼻端和尾流区的影响力逐渐降低；对气泡各阻力的能量耗散分析时发现，惯性力和表面张力的做功值变化微弱，对气泡上升速度的影响程度随气泡体积增加而逐渐降低。制约气泡上升速度增加的关键是，浮力做功增加的正功值被液膜区的黏性力和屈服应力做功共同消耗，最终表现为静止流体中Taylor气泡上升速度趋于定值。另外，表面张力对气泡上升速度的影响十分微弱，对浮力做功的耗散比例小于0.2%，对气泡上升速度的影响可以忽略。

参考文献：

［1］ DANG M， YUE J， CHEN G， et al. Formation characteristics of Taylor bubbles in a microchannel with a converging shape mixing junction［J］. Chemical Engineering Journal， 2013，223：99-109.

［2］ HAGHNEGAHDAR M， BODEN S， HAMPEL U. Experimental analysis of Taylor bubble behavior and mass transfer during lateral oscillation of a vertical milli-channel［J］. Chemical Engineering Journal， 2017，326：308-317.

［3］ 杨朝合，山红红，张建芳，等.传统催化裂化提升管反应器的弊端与两段提升管催化裂化［J］.中国石油大学学报（自然科学版），2007，31（1）：127-131，138.

YANG Chaohe， SHAN Honghong， ZHANG Jianfang， et al. Shortcoming of conventional RFCC reactor and advantage of TSRFCC technology［J］. Journal of China University of Petrolem （Edition of Natural Science）， 2007，31（1）：127-131，138.

［4］ 赵辉，喻芳，山红红，等.滴流床加氢裂化反应器内流体流动的数值模拟［J］.中国石油大学学报（自然科学版），2009，33（4）：136-140.

ZHAO Hui， YU Fang， SHAN Honghong， et al. Numerical simulation of fluid flow in hydrocracking trickle-bed reactor［J］. Journal of China University of Petroleum （Edition of Natural Science）， 2009，33（4）：136-140.

［5］ ABIEV R S.Bubbles velocity， Taylor circulation rate and mass transfer model for slug flow in milli-and microchannels［J］. Chemical Engineering Journal， 2013，227：66-79.

［6］ MASSOUD E Z， XIAO Q， EL-GAMAL H A， et al. Numerical study of an individual Taylor bubble rising through stagnant liquids under laminar flow regime［J］. Ocean Engineering， 2018，162：117-137.

［7］ AMANI E， AHMADPOUR A， TOHIDI M. A numerical study of the rise of a Taylor bubble through a sudden/gradual expansion in Newtonian and shear-thinning liquids［J］. International Journal of Mechanical Sciences， 2019，152：236-246.

［8］ YASUKAWA T， NINOMIYA W， OOYACHI K， et al. Enhanced production of ethyl pyruvate using gas-liquid slug flow in microchannel［J］. Chemical Engineering Journal， 2011，167（2/3）：527-530.

［9］ DE LOOS S R A， VAN DER SCHAAF J， DE CROON M， et al. Heterogeneous catalysis in a microchannel using a layer of carbon nanofibers on the channel wall［J］. Chemical Engineering Journal， 2012，179：242-252.

［10］ 魏發林，张松，丁彬，等.气/液介质对泡沫液膜渗透性的影响规律［J］. 油田化学，2022，39（4）：663-667.

WEI Falin，ZHANG Song，DING Bin，etal. Effect of gas/liquid properties on foam film permeability［J］. Oilfield Chemistry， 2022，39（4）：663-667.

［11］ 王刚，高金森，徐春明，等.提升管反应器中催化裂化与热裂化反应的模拟［J］.中国石油大学学报（自然科学版），2006，30（2）：110-114.

WANG Gang， GAO Jinsen， XU Chunming， et al. Simulating experiments on catalytic cracking and thermal cracking reactions in riser reactor［J］. Journal of China University of Petroleum （Edition of Natural Science）， 2006，30（2）：110-114.

［12］ LIU Y Q， ZHU K Q. Axialcouette-poiseuille flow of bingham fluids through concentric annuli［J］. Journal of Non-Newtonian Fluid Mechanics， 2010，165（21/22）：1494-1504.

［13］ LOU W， WANG Z， PAN S， et al. Prediction model and energy dissipation analysis of Taylor bubble rise velocity in yield stress fluid［J］. Chemical Engineering Journal， 2020，396：125261.

［14］ ARAJO J D P， MIRANDA J M， PINTO A， et al. Wide-ranging survey on the laminar flow of individual Taylor bubbles rising through stagnant Newtonian liquids［J］. International Journal of Multiphase Flow， 2012，43：131-148.

［15］ HUTTER K， WANG Y. Creeping motion around spheres at rest in a newtonian fluid［M］. Switzerland： Springe， 2016：1-45.

［16］ SOUSA R G， RIETHMULLER M L， PINTO A， et al. Flow around individual Taylor bubbles rising in stagnant CMC solutions： PIV measurements［J］. Chemical Engineering Science， 2005，60（7）：1859-1873.

［17］ DUBASH N， FRIGAARD I A. Propagation and stopping of air bubbles incarbopol solutions［J］. Journal of Non-Newtonian Fluid Mechanics， 2007，142（1/2/3）：123-134.

［18］ WANG Z， LOU W， SUN B， et al. A model for predicting bubble velocity in yield stress fluid at low Reynolds number［J］. Chemical Engineering Science， 2019，201：325-338.

［19］ LOU W， WANG Z， GUO B， et al. Numerical analysis of velocity field and energy transformation， and prediction model for Taylor bubbles in annular slug flow of static power law fluid［J］. Chemical Engineering Science， 2022，250：117396.

［20］ DE AZEVEDO M B， DOS SANTOS D， FACCINI J L H， et al. Experimental study of the falling film of liquid around a Taylor bubble［J］. International Journal of Multiphase Flow， 2017，88：133-141.

［21］ BENATTALAH S， ALOUI F， SOUHAR M. Experimental analysis on the counter-current Dumitrescu-Taylor bubble flow in a smooth vertical conduct of small diameter［J］. Journal of Applied Fluid Mechanics， 2012，4（4）：1-14.

［22］ FERSHTMAN A， BABIN V， BARNEA D， et al. On shapes and motion of an elongated bubble in downward liquid pipe flow［J］. Physics of Fluids， 2017，29（11）：112103.

［23］ GRIFFITH P， WALLIS G B. Two-phase slug flow［J］. Journal of Heat Transfer， 1961，83（3）：85-90.

［24］ NICKLIN D J. Two-phase flow in vertical tubes， Trans［J］.Transactions of the Institution of Chemical Engineers， 1962，40（1）：61-68.

［25］ MARTIN C S. Vertically downward two-phase slug flow［J］. Journal of Fluids Engineering， 1976，98（4）：715-722.

［26］ SIKORSKI D， TABUTEAU H， DE BRUYN J R. Motion and shape of bubbles rising through a yield-stress fluid［J］. Journal of Non-Newtonian Fluid Mechanics， 2009，159（1/2/3）：10-16.

［27］ MAJUMDAR A， DAS P K. Rise of Taylor bubbles through power law fluids： analytical modelling and numerical simulation［J］. Chemical Engineering Science， 2019，205：83-93.