空间薄膜结构粘接缝模型的建立与验证

操安博，林秋红，邱 慧，李 潇，刘志全

（北京空间飞行器总体设计部，北京 100094）

0 引言

空间大型薄膜结构在遮光罩、天线、太阳帆等领域具有广泛的应用前景。受限于薄膜生产技术，幅宽超过12 m、面积大于20 m2的大尺度薄膜结构难以一次成形。因此，空间大尺度薄膜结构往往需要由大量窄幅薄膜粘接而成［1］。此外，诸如抛物面薄膜天线［2］、张拉曲面遮光罩［3］等形状复杂的薄膜结构也难以直接成形，需用多片薄膜粘接成预期形状。粘接处的薄膜和胶层组成了粘接缝，粘接缝宽度（如下文图1 中的2c所示）一般为5～25 mm。为了进一步减轻薄膜结构的质量，未来空间薄膜结构粘接缝的宽度有望不超过10 mm。粘接缝的厚度明显大于其他位置的薄膜厚度，胶层具有不同于薄膜的刚度、强度，这就决定了空间大尺度薄膜结构内应力分布相比于不考虑粘接缝时的薄膜结构内应力分布有所不同。忽略粘接缝的影响将会导致薄膜的平面度、基频等重要技术参数偏离预期技术指标。然而，迄今为止，在空间大尺度薄膜结构高精度设计中还没有具有普适性的粘接缝模型。因此，开展空间薄膜结构粘接缝建模与验证对于大尺度薄膜结构的高精度设计具有重要意义。

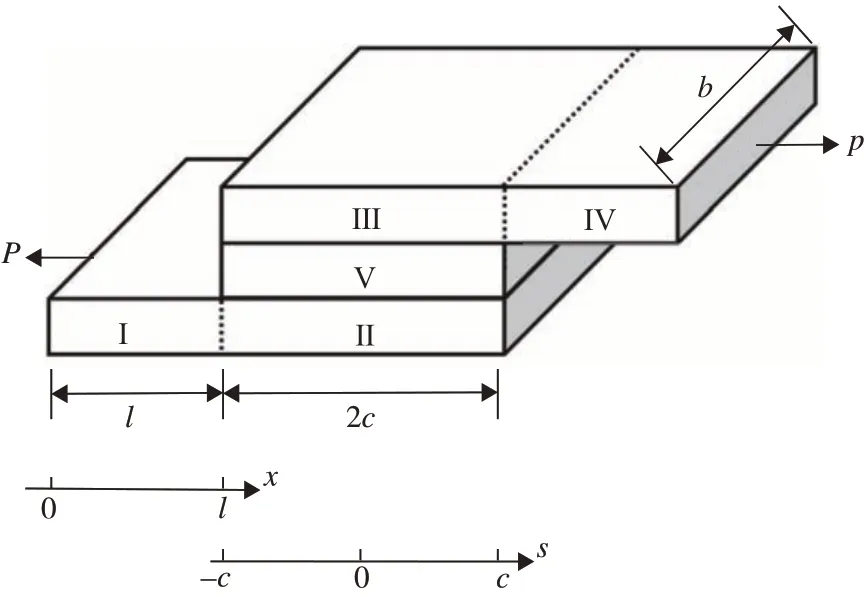
图1 薄膜粘接缝示意图Fig.1 Diagram of membrane adhesive bonded joint

在设计空间薄膜结构时，需要根据希望张拉得到的目标曲面形状，求解薄膜结构的初始形状以及维持目标曲面形状所需的预应力分布，这一过程称为找形。找形算法只能用于求解二维结构在空间中受力后的形状，因此薄膜［4］、支承柱［5］、张拉系统［6］等组件都必须作为二维结构进行建模。操安博等［7］将镀层引入了二维薄膜结构设计中，提出了能够使应力分布均匀化的设计准则。但是现有的空间薄膜结构力学建模中考虑了粘接缝的文献只有2010 年上海交通大学肖薇薇等［8］和2021 年东南大学潘粮今［9］的研究文献。文献［8］研究了粘接缝对薄膜结构褶皱的影响，发现粘接缝会明显降低薄膜的平面度。但是文献［8］的有限元仿真中用实体单元而不是内聚力单元来代表胶层，不能准确地体现胶层的粘性材料特征，且并未给出粘接缝二维模型的刚度和强度。文献［9］通过试验测量了特定设计参数下粘接缝的刚度和强度，并以薄膜遮光罩展开过程中应力最小为目标给出了最优的粘接缝布置方式。但是文献［9］中粘接缝的刚度和强度数据仅来源于特定场合下的试验，并未给出解析模型，在推广应用方面有一定难度。因此，有必要提出粘接缝的二维解析模型，得出粘接缝的刚度和强度特征。

由于粘接缝在厚度方向上具有非均质特征，需要将胶层、被粘接部分分别进行建模，因此前人对粘接缝的建模通常得到三维模型。1973 年，美国兰利研究中心的Hart-Smith［10］基于Volkersen 的线弹性模型和Goland 和Reissner 的刚体模型，考虑了上下被粘接部分的弯矩对胶层的影响，提出了最经典的板壳粘接缝模型。根据该模型计算得到的剪应力会在胶层边缘取得最大值。1977 年，英国皇家航空研究院的Allman［11］认为胶层边缘为自由边界，剪应力应为0，因此提出了胶层边缘自由的粘接缝模型。Allman 认为这一模型比较符合液体胶层固化后的实际情况，但并未对模型进行试验验证。1998 年，美国弗吉尼亚理工学院的Tsai等［12］认为被粘接部分也会受到剪应力作用，对Hart-Smith 模型进行了改进。2014年，巴西弗鲁米嫩塞联邦大学的Silva等［13］通过数字图像相关法测量了胶层边缘的弯矩，证明文献［12］的模型比较适用于被粘接部分剪应变大的情况。2010年，英国布里斯托大学的Zhao等［14］认为被粘接部分在粘接缝边缘不发生应变，提出了新的边缘弯矩计算方法。该模型适用于被粘接部分厚度大、刚度高的情况。2015 年，希腊帕特雷大学的Papanicolaou 等［15］通过试验和仿真，证明Hart-Smith模型无法应用于被粘接部分不对称的粘接缝，文献［14］的模型在此情况下更加适用。目前已有多种粘接缝模型在试验中得到了验证，被粘接部分包括金属、水泥［16］、复合材料板材等板壳结构。但是，应用Hart-Smith 等板壳粘接缝模型计算薄膜粘接缝的强度时［17-19］，求出的强度比试验结果小［9，20］，说明已有的三维粘接缝模型不适用于薄膜粘接缝。为了将薄膜粘接缝引入空间薄膜结构设计中，在推导出适用于薄膜的三维模型后，还需将三维模型映射到二维，才能得到空间薄膜结构设计所需的二维模型。

针对Hart-Smith 板壳粘接缝模型不适用于空间薄膜结构粘接缝的问题及空间薄膜结构高精度设计中粘接缝二维模型缺失的问题，本文拟开展空间薄膜结构粘接缝模型的建立与验证。首先基于Kirchhoff板理论建立空间薄膜结构粘接缝的三维模型；其次，将三维模型映射到二维，建立薄膜粘接缝二维等效模型；最后，对薄膜粘接缝二维等效模型进行仿真校验。本文提出的薄膜粘接缝二维等效模型可为空间薄膜结构高精度设计提供参考。

1 薄膜粘接缝三维模型的建立

空间薄膜粘接缝示意图如图1所示。

粘接缝由被粘接的下方薄膜II、被粘接的上方薄膜III和胶层V 这3部分组成。图中的I和IV 分别指粘接缝外的下方薄膜和粘接缝外的上方薄膜。粘接缝宽度为2c，长度为b。粘接缝外薄膜的长度为l。粘接缝上下方被粘接的薄膜通常为相同的薄膜，薄膜的杨氏模量、泊松比和厚度分别为E，ν和t。航天器使用的薄膜以各向同性薄膜为主，可以用E，ν计算出薄膜的剪切模量。被粘接的胶层杨氏模量为Ea，剪切模量为Ga，厚度为ta，下标a表示胶粘剂。胶层的剪切强度为τc，剥离强度为σc，下标c表示临界。本文假设薄膜粘接缝满足

此时可以不考虑粘接缝长度b对粘接缝内应力分布的影响。设粘接缝单位长度受到的拉力为载荷P。在I 部分上定义坐标轴x，I 部分上x的取值为［0，l］。在II、III、V 部分上定义坐标轴s，II、III、V 部分上s的取值为［-c，c］。假设I、II、III、IV 部分为Kirchhoff板，假设V部分为双线性内聚力材料。

对各部分进行受力分析，如图2所示。

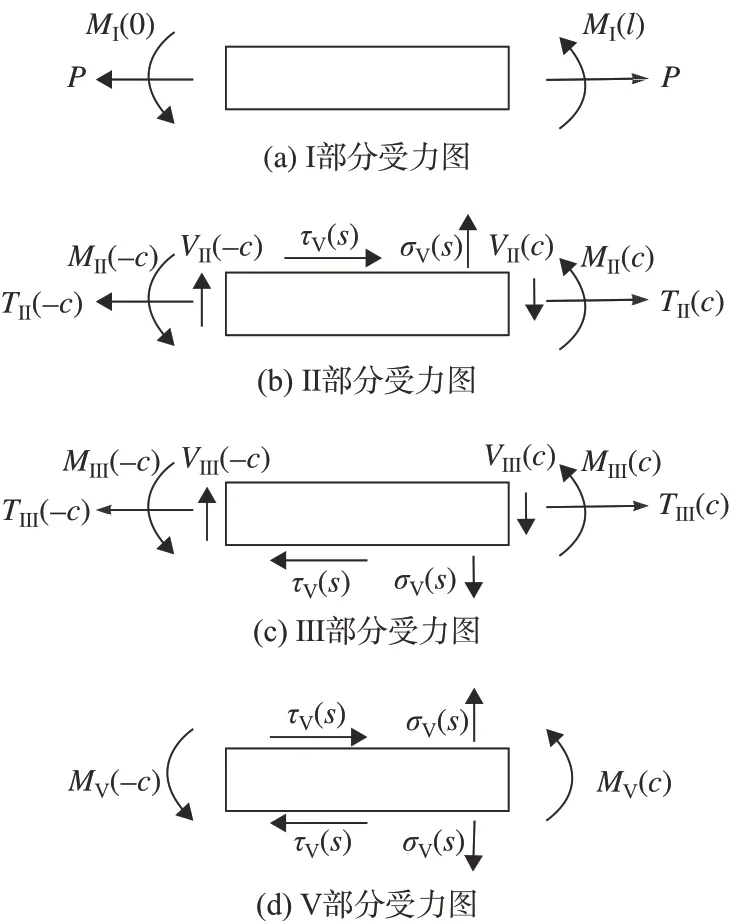
图2 薄膜粘接缝各部分受力分析Fig.2 Force analysis of membrane adhesive joint parts

I 部分受到的拉力就是粘接缝整体受到的拉力P，拉力为定值。I部分各处的弯矩为MI（x），在厚度方向上发生的位移为wI（x）。IV部分和I部分受力类似，但在后文的推导中不会用到，因此没有在图2中画出。

II 部分在宽度方向上受到的拉力为TII（s），在厚度方向上受到的拉力为VII（s），弯矩为MII（s），在宽度方向上发生的位移为uII（s），在厚度方向上发生的位移为wII（s）。V 部分对II 部分施加剥离应力σV(s)和剪应力τV(s)。III 部分在宽度方向上受到的拉力为TIII（s），在厚度方向上受到的拉力为VIII（s），弯矩为MIII（s），在宽度方向上发生的位移为uIII（s），在厚度方向上发生的位移为wIII（s）。III 部分同样受到σV(s)和τV(s)作用，但是σV(s)，τV(s)的积分方向与II部分相反，在图2中用相反箭头标出。

V 部分在宽度方向和厚度方向上不受拉力作用，受到的弯矩为MV（s），在厚度方向上发生的位移为wV（s），在宽度方向上发生的位移为uV（s）。V 部分受到的剥离应力为σV(s)，剪应力为τV(s)。

I部分受到的弯矩MI（x）可用式（1）计算

根据薄壳小变形假设，有

其中D为薄膜的弯曲刚度，用式（3）计算

式（2）的解为

其中A、B以及后文中出现的C、F均为微分方程解中的系数。微分方程的解中参数ξ的表达式如下

对于平面薄膜结构，在粘接缝外（x=0 处），应有MI(0)=0，代入式（4）有A1=0。

对II 部分、III 部分进行受力分析。力矩平衡方程

宽度方向力平衡方程

由应力应变关系，在宽度方向上的位移uII（s），uIII（s）满足下式

对于薄膜粘接缝来说，wII（s）和wIII（s）差距很小，近似有

对V部分进行受力分析，厚度方向力平衡方程

宽度方向力平衡方程

联立式（6）～（12），可得

对式（14）求导，联立式（6）～（12），有

其中λ是为了简化式（16）引入的参数，λ的表达式为

式（16）的解为

V 部分所受剪应力τV的积分为剪力，这个剪力与拉力P等大反向，从而有

由于薄膜粘接缝绕s=0 处中心对称，可知B3=F3=0。

由于下方被粘接薄膜在x=l、s=-c处连续，有wI（l）=wII（-c），并且wI（l）和wII（-c）的前2 阶导数相等。从而得到下式

薄膜粘接缝通常有ξl≫1，因此可以假设sinh(ξl)≈cosh(ξl)用于简化式（22）。

联立式（14）和式（18），有

联立式（22）～（23），可以求得MV(-c)的表达式

式（24）非常复杂，需要根据薄膜粘接缝中各参数的比例关系进行简化。文献［9］给出了t，ta，c，P的取值范围，文献［21］给出了E，ν的取值范围，文献［22］给出了Ea，Ga的取值范围，从而可以比较式（24）中各项的大小关系。简化后结果为

根据参数取值估算可知，根据式（25）求得的粘接缝边缘弯矩明显小于Hart-Smith 模型［10］，体现了薄膜粘接缝模型与板壳粘接缝模型的区别。

将MV(-c)代入式（23）可以求得A2，将A2代入式（19）可以求得C2。至此，式（18）中的参数均已求出，从而得到了胶层内剪应力τV(s)的表达式

对于粘接缝的力学性能，除了关注胶层内剪应力τV(s)外，还需要求出剥离应力σV(s)的表达式。联立式（6）、（8）、（9）、（11）有

其中χ是为了简化式（29）引入的参数，χ的表达式见式（30）

考虑到粘接缝具有中心对称性，式（29）的解为σV=A4cos(χs)cosh(χs)+B4sin(χs)sinh(χs)（31）

由整体结构不受厚度方向载荷可知，V 部分受到的剥离应力的合力为0，有

根据式（30）中各参数的取值范围可知χc≫1，从而简化式（33）为

联立式（34）和式（35），并且根据粘接缝的中心对称性取MV(-c)=MV(c)，有

由式（36）可以求得A4，将A4代入式（34）可以求得B4。至此得到了胶层内部剥离应力σV(s)的表达式，总结如下

求出τV(s)和σV(s)后，就可以求得图2 中所有物理量。式（26）和式（37）组成了薄膜粘接缝的三维模型。本文提出的三维模型与Hart-Smith 模型的核心差别在于弯矩的计算方法，即式（25）。

2 薄膜粘接缝二维等效模型的建立

建立薄膜粘接缝的二维等效模型，就是要建立一种宽2c、厚2t+ta的二维结构，使得这个结构具有与图1 中II、III、V 部分组合成的粘接缝相同的杨氏模量和强度，分别记作等效杨氏模量Ee和等效强度σe，下标e表示等效。由于粘接缝的失效可以分为由于剪应力达到极限和由于剥离应力达到极限两种形式，相应地将粘接缝的等效强度分别记作στe和σσe。

联立式（7）、（10）、（19），有

式（39）中等号右侧即为V部分受剪力发生的位移。V 部分的总位移为II 或III 部分的总位移与剪力导致的位移之和

由式（26）可知τV在+c和-c处取得最大值。因此当胶层由于剪应力达到剪切强度而失效时，有

代入A2、C2，并根据文献［9，21-22］简化式（42），有

此时粘接缝内部的平均应力即为粘接缝由于剪切发生失效时的等效强度στe，即

由式（37），由于χc≫1，MV(-c)＜0，σV的最大值近似为

代入MV(-c)，可以求出粘接缝由于剥离发生失效的等效强度σσe，即

式（41）、（44）、（46）组成了薄膜粘接缝的二维等效模型。该模型能够根据材料参数比较容易地得出粘接缝的刚度和强度，具有比文献［8-9］更好的普适性。

将空间薄膜粘接缝的各参数代入式（44）和式（46），可知στe≪σσe，说明粘接缝在失效时将首先由于剪应力达到极限而发生失效，这与试验结果［9，20］是一致的，因此不妨取σe=στe。στe的大小与粘接缝的宽度2c无关，说明粘接缝的等效强度不受粘接缝的宽度影响。

3 薄膜粘接缝二维等效模型的仿真校验

基于内聚力单元对胶层进行有限元仿真已经被证实能够比较准确地预测胶层的强度特征，与试验结果比较吻合［18-19］，因此本文使用有限元仿真对前文提出的薄膜粘接缝二维等效模型进行校验。将仿真模型中粘接缝整体受到的应力和应变之商作为等效杨氏模量的仿真结果，将胶层开始失效时粘接缝整体受到的应力作为等效强度的仿真结果。

在有限元仿真软件中，用COH3D8 内聚力单元模拟胶层，胶层的失效采用二次应力判据。用C3D8R体单元模拟薄膜。每个单元在粘接缝宽度方向上尺寸为0.1 mm。模型中各参数如表1所示。

表1 空间薄膜粘接缝设计参数Table 1 Design parameters of adhesive bonded joint

约束粘接缝在长度方向上的移动，从而使仿真模型符合b≫c≫t，ta的假设。将粘接缝IV 部分边缘绑定在控制点上，令控制点沿宽度方向运动，以控制点所受的反作用力为粘接缝受到的拉力P。计算粘接缝位移uV时，以图1 中V 部分右上边缘与左下边缘位移之差为粘接缝的位移。改变粘接缝宽度2c，计算粘接缝的等效杨氏模量和等效强度。

当2c在5 mm和25 mm之间变化时，Ee的变化规律如图3所示。

图3 Ee随2c的变化规律Fig.3 Ee versus 2c

由图3 可知，仿真求得的Ee以及根据式（41）求得的Ee均随2c的增加而增加并且趋于定值。仿真结果与式（41）求得的结果之差随2c增加而增大，当2c=5 mm 时，仿真结果为1.24 GPa，根据式（41）求得的结果为1.19 GPa，相差（（1.24-1.19）∕1.24）×100%=4.5%；当2c=25 mm 时，仿真结果为1.36 GPa，根据式（41）求得的结果为1.20 GPa，相差（（1.36-1.20）∕1.36）×100%=11.8%。说明本文提出的薄膜粘接缝二维等效刚度计算方法比较适用于2c≤10 mm的粘接缝。二维等效模型与Hart-Smith 模型在计算粘接缝等效刚度时差别极小，说明弯矩与等效刚度无关。仿真结果和解析方法求出的结果存在差异是因为，薄膜粘接缝受拉形变时呈现明显的非线性，二维等效模型及Hart-Smith 模型均无法消除非线性导致的误差。

当2c在5 mm 和25 mm 之间变化时，στe随2c的变化规律如图4所示。

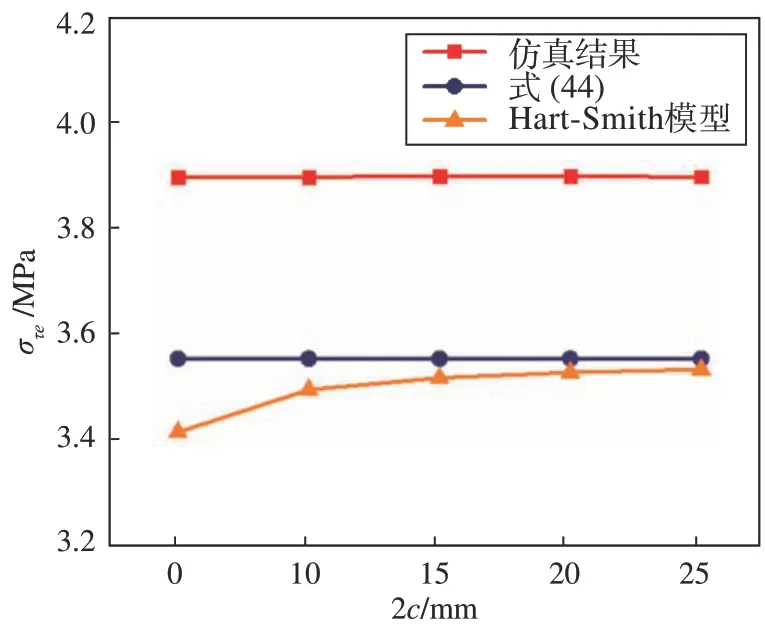
图4 στe随2c的变化规律Fig.4 στe versus 2c

由图4可知，根据式（44）求得的στe为3.55 MPa，仿真求得的στe为3.89 MPa，误差为0.34 MPa。两者均不会明显受到2c的影响，符合本文第2节由式（44）得出的结论。而根据Hart-Smith模型计算的στe会受到2c影响，并且随着2c增大趋近于二维等效模型求得的结果。Hart-Smith 模型在2c≤10 mm 时对στe的计算存在较大误差。当2c=5 mm时，根据Hart-Smith模型计算的στe为3.41 MPa，误差为0.48 MPa，二维等效模型将粘接缝的强度计算误差减小了（（0.48-0.34）∕0.48）×100%=29.2%；当2c=10 mm时，根据Hart-Smith 模型计算的στe为3.49 MPa，误差为0.40 MPa，二维等效模型将粘接缝的强度计算误差减小了（（0.40-0.34）∕0.40）×100%=15.0%。由于2c≤10 mm 有望成为未来空间薄膜结构的设计要求，本文提出的στe计算方法（式（44））能够解决Hart-Smith 板壳粘接缝模型不适用于宽度不超过10 mm 的空间薄膜结构粘接缝的问题。

4 结论

经过对空间薄膜结构粘接缝模型的建立与验证，得到研究结论如下：

1）基于Kirchhoff 板理论建立了空间薄膜结构粘接缝的三维模型（由式（26）和式（37）组成），将三维模型映射到二维得到的二维等效模型（由式（41）、式（44）和式（46）组成）相比Hart-Smith 模型，其强度计算误差减小了29.2%。当薄膜结构粘接缝宽度不超过10 mm 时，本文建立的粘接缝模型计算精度优于Hart-Smith板壳粘接缝模型。

2）建立了空间薄膜结构粘接缝二维等效模型，应用该模型能够根据材料参数计算得出粘接缝的刚度和强度。模型具有良好的普适性，为空间薄膜结构高精度设计提供了参考。仿真结果表明，根据二维等效模型求得的杨氏模量误差为4.5%～11.8%，且该误差与粘接缝宽度正相关。

3）仿真校验证实了粘接缝失效主要由剪切导致，并且粘接缝的等效强度不受粘接缝的宽度影响。