微纳卫星动量轮神经网络全局快速终端滑模控制
2023-12-28范书珲廖文和李磊磊
范书珲,廖文和,张 翔,李磊磊
(南京理工大学机械工程学院,南京 210094)
0 引言
随着信息技术和微机电技术的快速发展,微纳卫星已成为引领航天技术发展的引擎之一[1],广泛应用于通讯导航、环境监测以及深空探测等领域[2],在轨任务的复杂性也与日俱增,对其姿态控制能力提出了更高的要求。动量轮通过动量交换实现对卫星的姿态控制,其控制性能直接影响航天器姿态控制的精度、稳定性以及响应速度,进而影响卫星的寿命与在轨任务实现。相较于大卫星,微纳卫星所搭载的动量轮小巧轻便,更容易受到未知干扰等因素的影响。与此同时,微纳卫星在设计上缺乏一定的冗余性和容错能力,也增加了微纳卫星受到动量轮干扰影响的风险。因此为了开发先进的微纳卫星姿态控制系统,扩大微纳卫星应用场景,需进一步提升动量轮的控制性能,更大限度地发挥微纳卫星的性能潜力[3]。如图1所示,微纳卫星动量轮系统大多是由无刷直流电机(BLDC)驱动的飞轮体,该类电机是一种非线性时变系统,且存在电枢反应带来的不确定性因素,此外动量轮系统中还存在轮体不平衡、电压波动、摩擦力矩干扰、磁阻力矩干扰等引起的未知扰动。国内外研究者针对动量轮的控制开展了大量的研究,如文献[4]设计了改进的PID 控制器,提高了动量轮系统输出力矩的动态性能和稳态精度,但PID 控制由于无法兼顾动态响应和抗干扰要求[5],已无法满足未来微纳卫星的控制需求。

图1 微纳卫星动量轮系统组成Fig.1 Composition of momentum wheel system of micro-nano satellite
为了克服以上缺点,许多先进的控制策略如模糊控制[6],模型预测控制[7],滑模控制[8](SMC)以及神经网络[9]等方法被用来改善BLDC 转速控制精度与抗干扰性能,但每种方法都有一定的局限性。其中SMC 的设计与系统参数变化和负载扰动无关,且具有快速响应、控制简单等优点,更符合动量轮系统的控制要求[10]。但传统的SMC 仍然存在缺陷,如需要精确的动力学模型、存在有限时间收敛等问题。文献[11]设计了分数阶滑模控制器来加快收敛,提高控制精度,但是计算比较复杂。文献[12]采用积分滑模曲面来提高系统的控制精度,但系统状态收敛速度较慢。文献[13]引入了动量轮系统中摩擦阻尼、纹波电压和扰动力矩等干扰因素,建立了精确的动力学模型,并设计了等效滑模变结构控制器,虽然对干扰力矩有一定的抑制作用,但收敛时间也比较慢。文献[5]为了提高响应速度,提出一种双滑模面变结构控制方法,虽有一定的抗干扰能力,但是效果有限。而终端滑模控制算法的提出,保证了误差在有限时间内收敛到零,并确保了闭环系统的全局鲁棒性和稳定性[14]。文献[15]设计了一种固定时间终端滑模控制器,动量轮控制实现固定时间收敛,且对期望转速的跟踪效果比较理想。在终端滑模基础上,快速终端滑模以及全局快速终端滑模相继被提出。文献[16]利用快速终端滑模控制方法设计模块化控制器,文献[17]利用全局快速终端滑模将系统状态快速收敛至平衡点,均有效提高了系统的收敛速度以及鲁棒性,但是当模型参数不确定或者存在较大的外部干扰时,系统控制性能会大大下降。针对这一问题,常见的一种方法是设计自适应滑模控制器[18],采用自适应方法对系统中的未知不确定性参数进行估计。除此之外,神经网络由于其能够拟合任何非线性函数[19],具备处理复杂的输入输出映射的特性,可用来逼近系统中的不确定函数,得到了广大研究者的关注。文献[20]利用径向基(RBF)神经网络设计自适应律,提出了基于状态反馈的RBF 神经网络反步自适应控制算法,具备更强的鲁棒性,但系统收敛速度较慢。文献[21]为了处理未建模动态以及外部未知干扰等问题,将滑膜控制与RBF 神经网络结合,使系统在模型参数变化和外部干扰存在时具有更强鲁棒性的同时,提高了响应速度。文献[22]进一步提出了一种多核神经网络滑模控制方法,有效改善了系统的位置跟踪性能、干扰抑制能力和鲁棒性,但收敛速度仍有待提高。
本文考虑存在参数不确定性和外界未知干扰情况下,为进一步提高动量轮系统的响应速度以及抗干扰能力,从动量轮的组成和工作原理出发,建立了包括系统参数不确定性和外部干扰的系统动力学模型,并设计了一种将RBF 神经网络和全局快速终端滑模结合的自适应神经网络全局快速终端滑模控制(ANNGFTSMC)方法。该方法将系统参数不确定性和外界未知干扰统一归入到系统的总干扰中,然后利用神经网络估计并加以补偿。基于Lyapunov 方法设计了神经网络自适应律,增强了神经网络的逼近能力并且保证了闭环系统的稳定性,使动量轮系统具备更快的响应速度以及更强的抗干扰能力和鲁棒性等特点。
1 问题描述
本文研究的动量轮由无刷直流电机驱动,分析电机模型可以得到电压平衡方程、反电动势方程和力矩平衡方程:
式中:u为电机驱动电压,L为电机电枢电感,R为电机电枢电阻,i为电机电枢电流,e为电机反电动势,Ke为电机反电动势系数,ω为电机转速,Te为电机电磁转矩,Td为电机输出机械力矩,Tf为电机摩擦力矩,Kt为电机转矩系数,J为动量轮转动惯量,Kf为电机粘滞摩擦系数。
由此可以得到电机转速与驱动电压的理想关系式为
实际工作中,动量轮电机模型并不理想,由于动量轮电机采用全桥驱动方式,通过调整电压占空比来进行调速,电机驱动电压会受到电路输入电压的纹波影响,产生波动值Δu。此外,电机的摩擦力矩呈非线性,在电机运行中,其值会随工作环境发生变化,因此电机粘滞摩擦系数Kf可由标称值和不确定值两部分组成:Kf=Kf0+ΔKf,其中标称粘滞摩擦系数Kf0是电机设计过程中可测定的机械常数,不确定部分ΔKf是在实际工作过程中产生的不确定值。
由于动量轮在运行过程中还可能存在电机故障、动量轮轮体不平衡和轮体转动惯量不确定性等原因造成的未知干扰,为了提高动量轮系统的控制精度,在建立系统模型时需要考虑这些干扰对系统的影响,因此动量轮电机的力矩平衡方程可表示为
式中:Tx为动量轮系统中存在的外部未知干扰力矩。
由此可以得到动量轮输出转速与输入电压的关系为
为方便设计转速控制器,定义x1=ω,x2=,则动量轮电机系统可由如下状态方程描述:
当动量轮正常工作时,给定一个转速指令信号yd,系统会输出信号y去跟踪转速指令信号,控制目标描述为t→∞时,(y-yd)→0,其中系统输出信号y=x1,转速指令信号yd=xd。为方便后续控制器设计,现作出以下假设:
假设1.控制系统受到的不确定性d是有界的,存在正数ξ,满足|d|≤ξ。
假设2.控制系统的参数θ1,θ2,θ3在实际运行过程中是有界的。
假设3.系统的转速指令信号xd∈C2且是有界的。
2 控制器设计
2.1 全局快速终端滑模控制器设计
假设系统参数θ1,θ2,θ3准确值已知,且不考虑外部干扰时,状态方程可描述为
式中:α>0,β>0,p和q为大于零的奇数且0 <p<q。对s求导得:
为使控制系统对受到的干扰有更强的鲁棒性,将系统的控制量u分为等效补偿项u1和鲁棒反馈项u2,根据滑模面s=0 的到达条件,令=0,根据式(10)可设计如下控制器:
式(12)中:φ>0,γ>0,将式(13)代入式(10),可得:
引理1.假设存在连续正定函数V(t)>0,如果想要在有限时间ts内让V(t)收敛到0,必须满足以下不等式[23]:
定理1.对于控制系统(6),若假设1~3 成立,选取全局快速终端滑模面(8),根据引理1,在控制器(11)~(13)的作用下,系统能在有限时间内到达滑模面s=0,实现有限时间稳定。
证.设计李雅普诺夫函数如下:
根据引理1可得,系统(6)能在有限时间内到达滑模面s=0,且到达时间满足:
2.2 神经网络全局快速终端滑模控制器设计
控制器(12)是在系统参数θ1,θ2,θ3准确值已知且未考虑外部干扰情况下建立的,因此这种控制器在实际运行中的控制精度并不能达到预期效果。为解决上述缺陷,本部分引入RBF 神经网络,设计了ANNGFTSMC。
系统状态方程中的参数θ1,θ2,θ3在运行过程中存在不确定性,令参数的名义值为θ1n,θ2n,θ3n,参数不确定项为Δθ1,Δθ2,Δθ3,可得θ1=θ1n+Δθ1,θ2=θ2n+Δθ2,θ3=θ3n+Δθ3。原控制系统(5)可由如下状态方程描述:
为处理未知项,总干扰描述为
将式(22)代入式(21)可得:
本文采用RBF 神经网络观测器估计总干扰,神经网络结构示意图如图2所示。
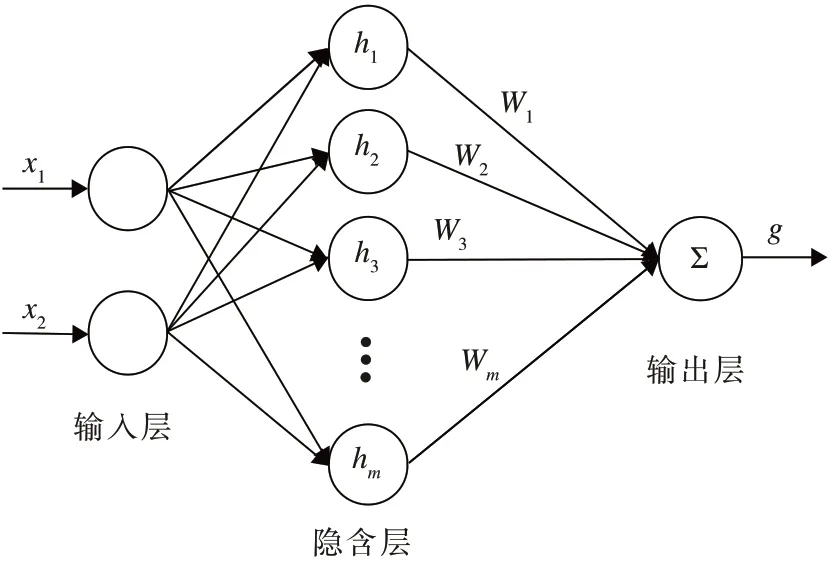
图2 神经网络结构示意图Fig.2 Structure of neural network
RBF神经网络的拟合公式为[24]
式中:W为隐含层到输出层的权重,x为网络的输入,h(x)=[h1(x),h2(x),…,hm(x)]T为神经网络隐含层各个节点的激活函数输出,m为网络隐含层节点数,ς为网络的逼近误差,g为网络输出。
本文采用的网络激活函数是高斯径向基函数[25],其表达式为
式中:ci和σi分别为第i个神经元高斯函数的中心参数向量和宽度。
利用RBF 神经网络观测总干扰D,由神经网络的逼近特性可得,存在理想权值向量WT使得:
式中:x是状态量x1和x2组成的矩阵。由于神经网络的权值向量W未知,令为W的估计值,则总干扰的估计,重新设计控制器:
式中:λ>0。
定理2.在式(27)、式(28)、式(29)和式(34)的作用下,动量轮系统可以实现有界稳定,并且系统转速误差e将在有限时间内收敛到0。
证.设计李雅普诺夫函数如下:
通过设定式(38)中α,β,p,q参数,可以调节系统的收敛速度。
控制流程图如图3所示。
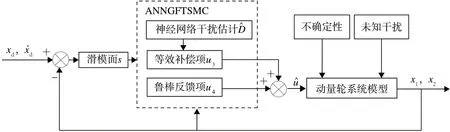
图3 控制流程图Fig.3 Control strategy diagram
3 仿真校验
为验证本文提出的ANNGFTSMC 的有效性,对动量轮控制系统进行仿真,并和滑模控制[13](SMC)方法、全局快速终端滑模控制(GFTSMC)方法以及神经网络滑模控制[22](ANNSMC)方法在转速响应和抗干扰能力上进行对比。仿真中选取动量轮系统参数见表1。

表1 动量轮系统参数Table 1 Model parameters of the momentum wheels
根据实际调试,GFTSMC 控制器参数选取为α=40,β=2,p=7,q=9,φ=0.005,γ=0.005,ξ=0.5;ANNGFTSMC 控制器参数选取为α=80,β=2,p=7,q=9,φ=0.005,γ=0.005,η=0.5,λ=0.5×10-6。
为方便比较,仿真实验设置了以下几种工况:
工况1:正常调速情况,系统只受到模型不确定性及摩擦、电压纹波等干扰;
工况2:动量轮在稳态工作时,系统受到较大的外部脉冲力矩干扰;
工况3:动量轮在稳态工作时,系统受到较大的外部周期性力矩干扰。
3.1 正常调速
仿真实验中,根据微纳卫星姿控系统常用的控制策略制定仿真条件,动量轮初始转速给定1 000 r·min-1,之后系统进行一秒一控的调速过程。如图4 所示为Case 1 的转速响应曲线,可以看出各种控制方法都可以使转速较好的跟踪控制指令,而且没有超调。在转速增加50 r·min-1时,GFTSMC 和ANNGFTSMC 较SMC 和ANNSMC 更快到达平衡状态,时间约为0.05 s;转速减小150 r·min-1时,SMC和ANNSMC 经过约0.15 s 到达平衡状态,而GFTSMC和ANNGFTSMC 依然更快到达了平衡状态,平衡时间约为0.1 s。综上可知本文设计的GFTSMC 和ANNGFTSMC 无超调,收敛时间短,有更快的响应速度。
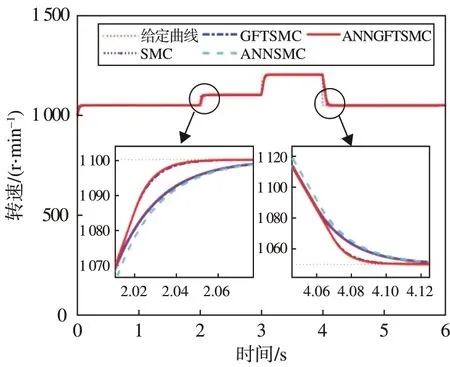
图4 Case 1的转速响应曲线Fig.4 Rotational speed response curves of Case 1
3.2 脉冲干扰力矩
仿真实验中,在t=2 s 时施加0.1 Nm 的脉冲干扰力矩。如图5 所示为Case 2 的转速响应曲线,分析可得,施加脉冲干扰力矩后,SMC、GFTSMC 转速出现明显波动,ANNSMC 以及ANNGFTSMC 的波动较小。Case 2仿真跟踪误差最大值与收敛时间统计见表2,可以看出ANNSMC 与ANNGFTSMC 收敛时间均约为0.02 s,而ANNSMC 的转速跟踪误差最大为0.789 8 r·min-1,ANNGFTSMC 的转速跟踪误差最大为0.151 8 r·min-1,因此在脉冲力矩干扰的情况下,ANNGFTSMC 控制器可以在很短的时间内更优的克服扰动变化,具备更强的抗干扰能力。
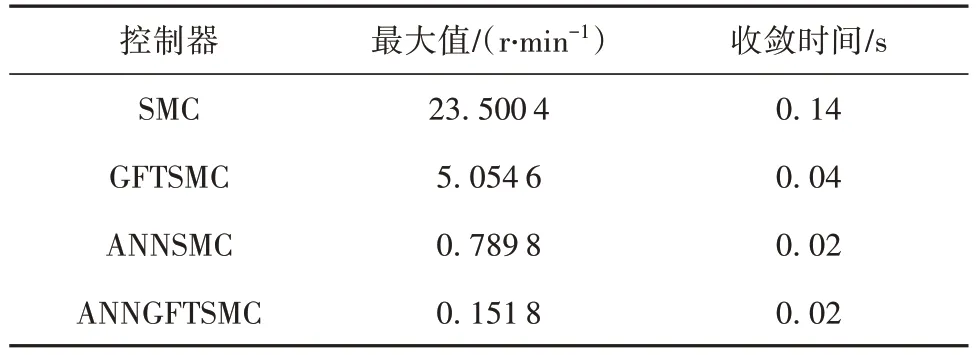
表2 Case 2仿真跟踪误差最大值与收敛时间Table 2 Maximum tracking error and convergence time of each controller in Case 2

图5 Case 2的转速响应曲线Fig.5 Rotational speed response curves of Case 2
3.3 周期性干扰力矩
仿真实验中,在t=2 s 时施加dt=0.05 sin(10t+4.74)+0.02 的周期性干扰力矩。如图6~7所示分别为Case 3的转速响应曲线和跟踪误差曲线,Case 3仿真跟踪误差效果统计见表3。由图6~7可以看出,施加周期性干扰力矩后,ANNSMC 与ANNGFTSMC相较于另外两种控制方法,系统转速控制跟踪曲线基本与给定信号曲线重合,转速没有明显波动。分析表3 可得,SMC 和GFTSMC 的误差平均值与标准差较大,而ANNSMC 与ANNGFTSMC 由于对外部干扰和模型参数不确定性等进行估计与补偿,误差的最大值、平均值与标准差相较于另外两种控制器都非常小。进一步分析表3 可以看得出本文设计的ANNGFTSMC 相较于ANNSMC 最大值、平均值与标准差更小,证明了本文算法在存在周期性干扰力矩转的情况下,具备更好的转速跟踪性能以及更强的抗干扰能力。
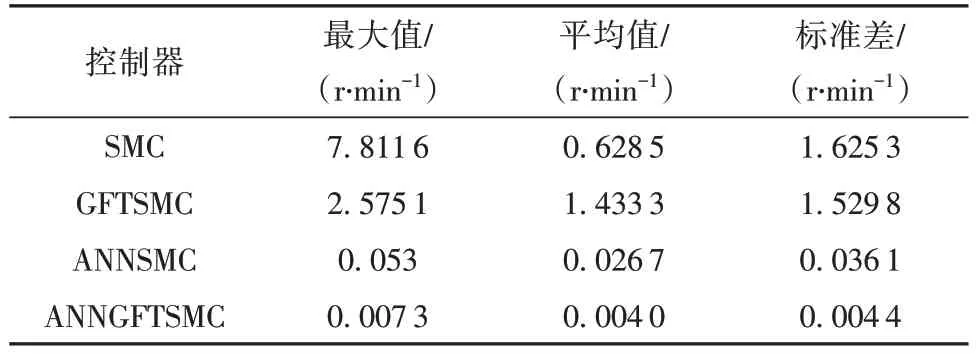
表3 Case 3仿真跟踪误差效果统计Table 3 Tracking error effect of each controller in Case 3

图6 Case 3的转速响应曲线Fig.6 Rotational speed response curves of Case 3

图7 Case 3的转速跟踪误差曲线Fig.7 Rotational speed tracking error of Case 3
ANNSMC 与ANNGFTSMC 的干扰估计如图8 所示,神经网络观测器主要观测的是未知干扰和参数不确定性的总和,从图8 可以看出,ANNGFTSMC 对外部未知干扰的估计精度更高。
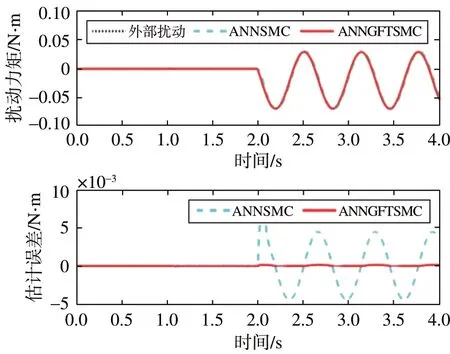
图8 ANNGFTSMC干扰估计Fig.8 Disturbance estimation of ANNGFTSMC
4 结论
针对微纳卫星动量轮控制系统,考虑系统中存在的参数变化和外界未知干扰等不确定因素,本文提出了一种自适应神经网络全局快速终端滑模控制(ANNGFTSMC)方法,并通过仿真对比得到了以下结论:
1)设计的GFTSMC 与ANNGFTSMC 控制方法相对于SMC以及ANNSMC具备更快的响应速度。
2)设计的ANNGFTSMC 控制方法对外界未知干扰的估计误差相较于ANNSMC 更小,且相对于SMC、GFTSMC 具备更强的抗干扰能力和鲁棒性,可有效提高动量轮系统转速控制精度。
3)通过仿真对比验证了控制器的有效性,对探索新型微纳卫星动量轮的控制策略具有一定的参考价值,为进一步扩大微纳卫星应用场景,发挥微纳卫星的性能潜力奠定了基础。
