大型星座混合模拟退火遗传算法测控任务规划

马林，秦 阳，秦嘉豪，徐 明

（1.航天工程大学宇航科学与技术系，北京 101416；2.中国航天科技集团有限公司，北京 100048；3.北京航空航天大学宇航学院，北京 102206）

0 引言

随着大型星座的规模逐渐扩大，星座的测控业务工作量激增。传统的人工编排测控调度方案的方法由于耗时长、任务完成度低，已经无法适应当前大型星座测控业务调度管理的需求。多星测控调度问题（Multi-satellite TT&C scheduling，MSTCS）问题是指在多星测控需求和测控资源一定的条件下，研究如何对大量卫星的各种测控需求进行管理和调度，通过合理地分配测控资源，更好地满足卫星测控的需求，使得卫星发挥最大的效能，并对星座的总体设计提供指导建议［1］。多星测控调度问题是一个经典的NP-Hard 问题，是复杂调度问题的一个具体形式。复杂调度问题的可行解空间庞大，约束条件多样，且具有关联性。因此，通过遍历可行解空间的方法难以在多项式时间复杂度内得到问题的满意解。

为了解决多星调度问题，国内外涌现出许多相关研究。关于多型调度的研究大多采用先建立数学模型，再采用合适的智能算法进行求解的方法。现有研究中采用的数学模型包括数学规划模型、约束满足模型等，采用的智能算法包括粒子群算法、禁忌搜索、模拟退火算法、蚁群算法、遗传算法以及机器学习和深度学习等方法。

针对多个点目标的成像调度任务规划研究。贺仁杰［2］进行了成像卫星有效载荷任务规划的研究，提出了约束满足模型和混合整数模型，并采用多种启发式算法进行了求解，但是没有在任务规划中考虑卫星的测控问题。Liu 等［3］研究了多星有效载荷任务规划问题，将任务规划分解为任务分配和动作序列生成两个子过程，并采用启发式算法进行了求解。丁祎男等［4］提出一种多目标变邻域模拟退火算法，兼顾了成像星座观测任务的完成度和成像质量。韩鹏等［5］基于相对成像时刻编码方式，提出了一种适用于敏捷成像卫星任务规划的自适应遗传算法。Kulkarni 等［6］将卫星测控调度问题建模为0-1 背包问题，并采用智能算法进行了求解，但是算法的收敛速度较慢。Zhang 等［7］，Wang 等［8］和Wu等［9］分别采用蚁群算法、启发式算法和NSGA-III 对多星调度问题进行了求解，但是没有对算法进行进一步的优化。Spangelo 等［10］研究了单卫星多地面站通讯问题，但是不适用于大型星座多星测控问题的求解。Gao等［11］研究了采用并行计算的多星任务规划算法，加快了算法收敛速度。Chang 等［12］研究了多星载荷任务规划问题，采用了智能算法进行求解，但是没有考虑卫星数传。

针对多个区域目标或大范围区域目标的成像调度任务规划研究，Zhu 等［13］提出了一种分阶段的星座观测大范围区域目标的任务规划方法，但没有考虑卫星的星上存储约束，没有综合考虑数据下传。甘岚等［14］针对太阳同步圆轨道卫星星座对地观测任务，研究了在卫星机动情况下对多区域目标的成像任务规划算法，实现了星座对于多目标区域覆盖率的优化。Zhao 等［15］提出了一种基于禁忌搜索的多星任务规划方法，但仅针对多个点目标，没有考虑星上存储约束。Li 等［16］提出了采用多目标优化的卫星集群任务规划方法，但没有考虑卫星星上存储约束，没有综合规划卫星数据下传。Chen等［17］提出了一种基于整数序列编码的姿态敏捷卫星任务规划方法，给出了目标可见窗口的分布规律以及冲突定义方法。Fan 等［18］提出了基于任务有向图的多星任务规划方法，考虑了任务之间的相关性，将多区域观测问题建模为0-1 规划问题，采用启发式算法进行求解，最大化任务时效性，但在任务规划过程中没有考虑卫星的星上存储资源以及能源约束，并且没有综合考虑观测数据下传。Wu等［19］将启发式算法和精确算法相结合，采用分立-整合规划框架，实现对地观测星座针对区域目标的任务规划。Chen 等［20］采用有集成的多通道神经网络，通过神经网络预测加单星本地规划的方法，实现任务方案的快速生成，提高任务规划的实时性，通过与高性能启发式算法的比较，验证了多通道神经网络算法在任务方案生成效率以及任务效能上的优势。Song 等［21］建立了多星任务规划的混合整数编码模型，首先采用改进的烟花算法进行不可分割任务的规划，之后采用启发式规则进行长时连续跟踪观测任务的任务规划。针对多星测控和数传任务规划问题，Chen 等［22］建立了最大化任务收益和任务完成率的多星任务规划约束满足模型，在遗传算法中加入种群扰动和低适应度个体淘汰策略。采用遗传算法获得任务分配方案，之后采用本地任务规划算法决定任务的实际执行序列。Zhang等［23］提出了一种采用遗传编程的多树搜索算法，实现了考虑卫星轨控的多星任务规划。Khojah等［24］采用重力梯度算法实现多目标优化，并且采用粒子群方法增强了算法的全局搜索能力。Berger 等［25］采用二次规划方法建立了多星任务规划模型，提出了NP-Hard 问题的最优上界，但是由于算法求解时间较长，不适用于工程任务规划使用。Xu 等［26］提出了基于高斯投影的大规模区域目标动态分解方法，并通过整数规划实现星座对于大规模区域目标成像的任务规划，但是没有考虑星座的成像数传。

为了提供专门应用于多星测控任务规划的有效方法，本文提出了基于拥挤度的混合模拟退火多层编码遗传算法。遗传算法具有全局寻优能力，且算法结构清晰，便于针对具体问题进行修改，而且模块化的算法结构便于在算法流程中加入其他启发式操作，以提升算法性能。模拟退火可以通过设置降温速率调节收敛速度，以每一代最优个体为起点进行模拟退火，提高算法收敛速度和种群多样性。通过在真实卫星系统中的实验验证了本文提出方法的可行性和高效性。

1 多星测控问题描述

多星测控调度问题可以描述为：包含m个各类测控天线的天线集合，为包含n个卫星的大型星座提供时段 内的测控服务。每个卫星在这一时段内需要安排若干个测控弧段。每个卫星的测控只能由固定一种或几种天线进行，需要的测控时间长度各不相同。每个天线在同一时刻只能对一颗卫星进行测控。多星测控问题涉及的数学符号的定义如表1所示。

表1 数学符号定义Table 1 Definition of mathematical symbols

采用约束满足模型（Constraints Satisfy Problem，CSP）对多星测控问题进行数学建模，其CSP 模型包括目标函数和约束条件两部分，数学形式为

目标函数为最大化综合收益，形式化描述为式（1）。目标函数是指标f1，f2，f3的线性组合，各个优化指标的形式及其对方案优劣的影响分析如下。代表最大化调度方案的任务完成率。多星测控任务规划的目标是采用有限的测控天线资源，在有限时间内尽量满足更多卫星的测控任务，因此需要计算待安排测控任务的完成率，作为表征任务规划结果方案优劣的指标代表最大化所有安排任务的优先级之和，其中pi为任务i的优先级。由于任务的重要程度不同，仅考虑全局的任务完成率并不足以完全反应任务方案的优劣，还需要进一步计算归一化的任务优先级之和，作为评价指标之一，扩大高优先级任务的成功安排对任务规划结果方案评价函数的影响。f3=E(θ)-S(θ)代表最大化所有任务弧段仰角的均值，并最小化仰角的方差，其中θ代表任务弧段的最大仰角。在测控任务中，高仰角的弧段不仅可用测控时间更长，而且通信受云层、大气衰减的影响更小，因此计算所有安排任务的弧段仰角作为方案优劣的评价指标之一。但仅考虑所有弧段的仰角之和最大并不能保证任务方案最优，一些大仰角弧段的安排可能对测控方案仰角之和产生较大影响，但同时挤占测控天线资源，并导致其他多个任务的测控仰角过小。因此，需要同时计算所有任务仰角的方差，作为惩罚项，防止任务间弧段仰角差异过大。可行调度方案必须满足五个约束条件，各个约束条件的含义如下。第一，颗卫星的测控必须由指定类型天线进行，如式（2）。第二，同一卫星不能同时占用多个天线，如式（3）。第三，同一天线上安排的相邻测控任务时间间隔必须大于最小任务切换间隔，如式（4）。第四，测控弧段的时长必须大于测控任务所需的最小时长，如式（5）。第五，测控任务必须安排在任务最早开始时间和任务最晚开始时间内，如式（6）。

2 混合模拟退火遗传算法求解多星测控问题

为求解多星测控问题，首先，需要获取任务规划时段内所有卫星与所有地面站之间的可用测控弧段，作为任务方案的搜索空间。第二，通过设计编解码规则，建立任务方案到多层编码整数序列之间的映射。第三，通过设计遗传算子实现任务方案的进化和全局搜索。第四，通过加入基于拥挤度的模拟退火操作，在进化过程中平衡星间任务拥挤度，提高任务方案优化速度与任务方案质量。

2.1 卫星可用测控弧段计算模型

进行大规模星座数传任务规划的前提是获取星座与地面站系统中所有地面站之间的可见弧段，作为星座数传任务规划的搜索空间。本节给出地面站对目标航天器的可见弧段计算方法。地面站位于地球表面，与卫星的可见性取决于地面站相对于航天器的仰角，如果仰角大于一个最小临界值，并小于一个最大临界值，则地面站与航天器之间物理可见，反之则地面站与航天器之间不可见。如图1所示。

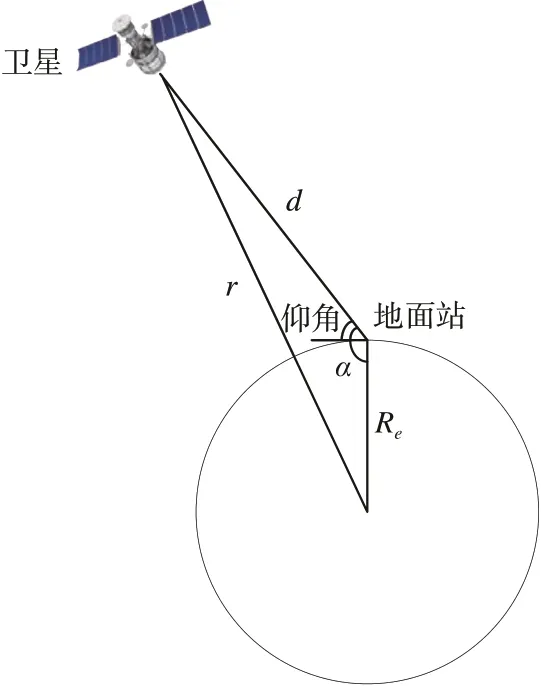
图1 地面站与卫星可见性示意图Fig.1 Diagram of visibility between ground station and satellite

设地面站经纬度位置为(λ，φ)，高程为H，可以计算得到地面站在地球固连坐标系下的坐标(xT，yT，zT)，即

根据航天器当前轨道根数，可以计算航天器在地心固连坐标系下的坐标(xS，yS，zS)，因此，航天器与地面站之间的距离为

由图1 的三角形关系，可由d，Re和航天器的地心距r计算出地面站与航天器连线和地面战与地心连线之间的张角α1，即

显然，如果αmin≤α1-90° ≤αmax，则地面站与航天器之间物理可见，且满足测控连通性要求，否则两卫星物理不可见，地面站当前时刻不能实现对航天器的测控。采用递推方法可以获得一个圈次内地面站对目标航天器的可见弧段。以Δt作为时间步长进行卫星的轨道外推，采用上述方法判断轨道外推的各个时间节点地面站与卫星是否可见，在一个圈次的轨道外推过程中，地面站与卫星的初始可见时刻与末端可见时刻之间的时段即为本圈次卫星与地面站的可见弧段。可见弧段的计算精度主要取决于仿真推进的时间步长，步长越小精度越高，步长越大获得的可见窗口精度越低。在本文中，推进步长取Δt=1s。

2.2 可行解编解码规则设计

采用多层编码方法，染色体为一个整数序列。若待安排卫星的数量为n，每个卫星的待安排测控任务数量为pi，则染色体的长度为染色体的前半段的基因位是卫星的序号，后半段的基因位是对相应位置上卫星进行测控的天线。在同一条染色体中，某一卫星的序号出现的第k次，代表该卫星的第k次测控任务。例如3 个卫星，每个卫星需要安排3 次测控任务，则卫星序列可以为（3，1，2，2，1，3，1，2，3）。其中1，2，3 分别表示不同的卫星，序列中从左到右的三个1 代表卫星1 的三次测控任务，2和3与1类似。

解码方法将染色体转化成一个可行调度方案。在本文的算法中采用启发式规则进行解码。首先，将个体基因的编码整数串解码为各个天线上待安排的任务序列。染色体组成如图2 中（a）所示。按照染色体前半段的卫星序列逐一进行解码，将任务按照顺序加入对应天线的待安排任务序列，获得每个天线的任务弧段安排顺序，如图2（b）所示。其次，按照每个天线上卫星序列的先后顺序，选择可行弧段，并记录卫星和天线已占用的时长。解码弧段分配规则如图3所示。

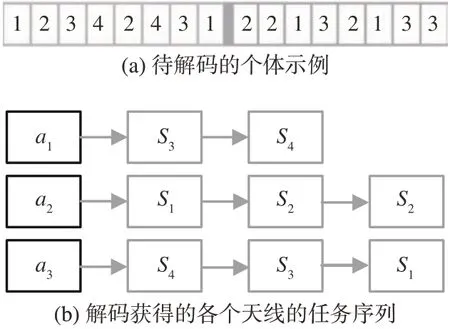
图2 待安排任务序列解码过程示意图Fig.2 Decoding of task sequences to be preformed

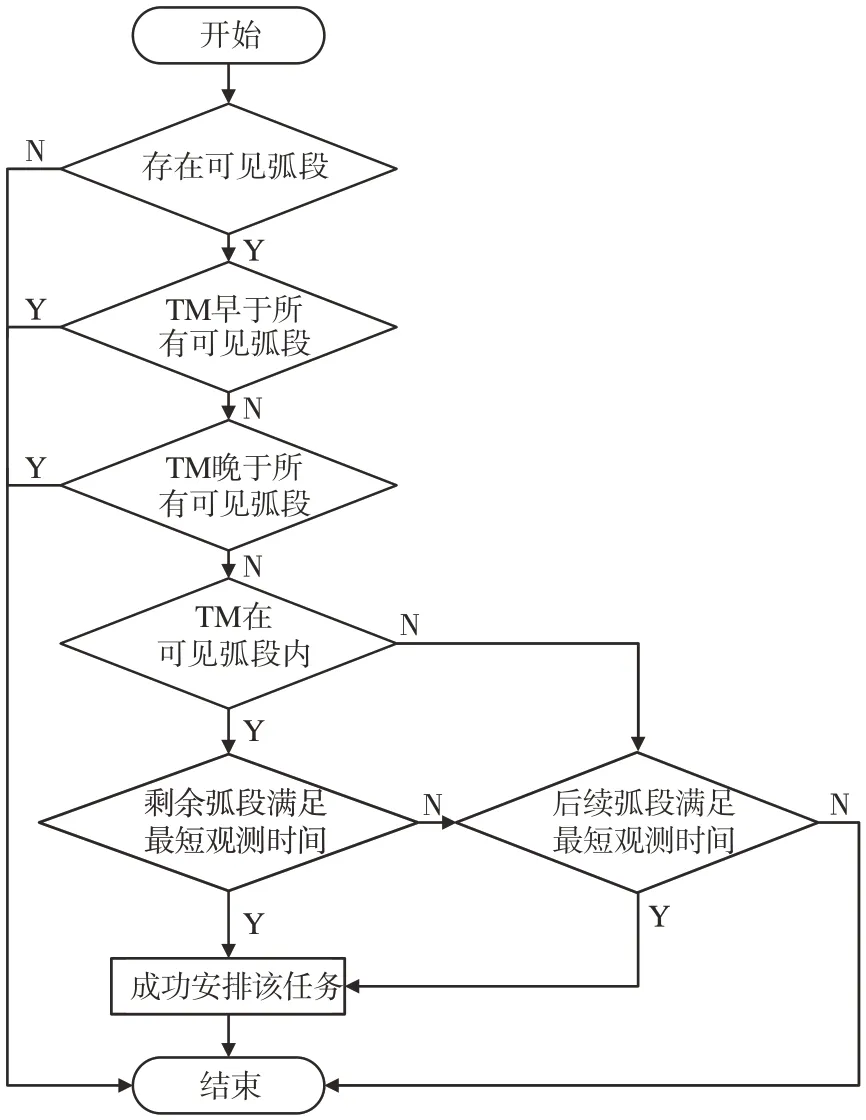
图3 解码过程中的弧段分配规则Fig.3 Feasible window allocation algorithm in decoding process

按照卫星测控任务的特性，针对中低轨道卫星，一般情况下使用整轨安排模式。首先读取天线当前已占用时段的终止时刻TM，并搜索TM之后的待安排卫星可用弧段，将整段弧段安排给当前任务。针对中高轨道卫星，由于卫星轨道周期较大，与地面站的可见窗口经常长达数小时，浪费了天线测控资源。此时继续采用整轨安排的方法不合理，因此需要通过最短任务时长进行解码。针对每个任务，首先判断任务时间区间内地面站与该卫星有无可见区间，当地面站与卫星无可用弧段时，表明该任务在当前规划时段内无法完成，放弃该任务。TM为卫星当前解码已占用时段的终止时刻。当TM早于或晚于所有可见弧段时，表明任务在当前规划时段内无法完成，放弃该任务。当TM不在某一可见弧段内部时，通过向后寻找大于最短测控时间需求的弧段安排该测控任务。如果TM恰好在当前待安排卫星任务的某个测控窗口内，首先判断剩余的弧段是否满足最短测控时间要求。在当前测控时段不满足最短测控时间要求时，向后搜索后续可见弧段，直至任务成功安排。

2.3 遗传算子设计

在本文设计算法中，选择算子采用轮盘赌方法。轮盘赌选中某个子代个体的概率与该个体的适应度成正比，适应度较大的染色体被选中的概率大，适应度较低的染色体被选中的概率小。轮盘赌既保证了种群向着适应度提高的方向进化，又保留了种群的多样性，防止遗传算法早熟。交叉算子采用随机单点交叉。在两染色体交换某一片段之后，可能会出现卫星序列中基因的缺失或冗余，因此需要对染色体进行合法性检查，并修复不合法的染色体。变异算子采用随机基因座变异，即随机交换两个卫星编号的顺序。在变异之后可能会出现天线基因不合法的情况，因此也需要进行染色体合法性检查，并修复不合法的染色体。各个遗传算子的具体操作在2.3.1至2.3.3中详细描述。

2.3.1 选择算子

选择算子在任务方案种群进化过程中起着决定性作用。选择操作淘汰掉种群中适应度较低的部分个体，并使得适应度较高的个体具有更大的生存机会，使其基因在种群中占有更高的支配地位。为了防止初始化过程中适应度较高的部分个体的基因占优而导致种群提前收敛到局部最优解，而无法抵达全局最优，本文采用轮盘赌方法进行选择操作，个体的适应度值按照其目标函数值进行线性排列分配，并按照适应度值构造轮盘，即保证了高适应度个体的基因占优，又保证了种群多样性，避免局部收敛。

2.3.2 交叉算子

交叉操作是遗传算法进化的核心机制，种群中个体通过交叉获得基因的重新组合，优秀的重组个体在下一代的选择操作中更容易存活。在通过选择操作生成子代种群之后，通过交叉概率pc决定种群中的个体是否进行交叉操作，对进行交叉操作的部分个体，进行随机两两匹配，采用单点交叉的方法，在任务序列段随机产生交叉点位，并完全交换两个体在交叉点位之后的任务序列和天线序列。由于两个体的基因序列无关，而在交换了序列之后，会出现部分任务在任务序列中多次出现，这与单个任务只能由某一资源执行一次的任务规划约束，即式（3），发生了冲突，因此必须修复不合法的交叉结果。如图4 所示，首先遍历基因中各个卫星测控任务数量与待安排任务数量是否一致。针对不一致的冗余任务，找到对应的缺失任务，并采用缺失任务的基因对冗余任务进行替换。

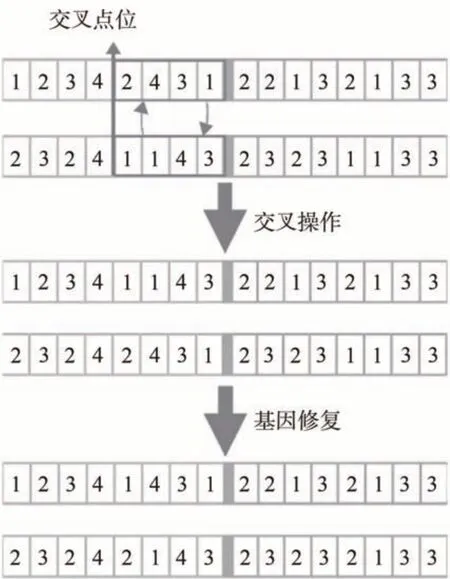
图4 交叉操作及其染色体修复过程示意图Fig.4 Crossover operation and chromosome restoration

2.3.3 变异算子

变异操作是遗传算法种群中个体产生新性状的核心操作，种群中个体的基因点位通过随机的变异产生新的基因组成，维持种群基因的多样性，增强算法全局搜索能力。在交叉操作之后，种群的基因组成已经进行了重组，为产生新的基因组成，还需要进行变异操作。通过变异概率pm决定种群个体是否发生变异。变异过程为随机基因点位变异，即随机选择两个任务序列中的基因点位，并交换其基因。

由于变异过程仅交换了卫星基因，而没有交换对应的机器基因，可能引起变异点位的机器基因超出该卫星的可用测站集合上限，这与测控任务必须由卫星的可选天线集合中的天线执行的约束条件，即式（2）冲突，因此必须对变异后的染色体进行检查和修复。修复过程如图5所示。判断变异卫星基因对应的机器基因是否超出了该卫星可用机器集合数目上限，如果判断超出上限，则重新初始化对应的机器基因。

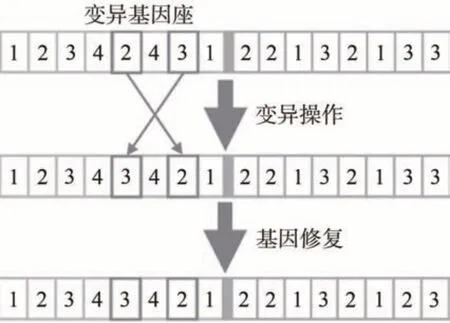
图5 变异操作及其染色体修复过程Fig.5 Mutation operation and chromosome restoration

2.4 基于拥挤度的快速模拟退火

通过2.3节所述的单纯遗传算法机制可以对多星测控问题的优秀调度方案进行搜索，但经过对遗传算子的分析可以发现，对于种群的进化起重要作用的交叉算子仅改变了每个天线对应卫星序列的先后顺序，而不同天线之间的卫星序列没有交流。只有变异过程可能引起不同天线的卫星序列之间的交流。而变异操作是不定向的，不能保证染色体向着适应度高的方向改变。变异概率过高会导致种群稳定性变差。通过提高变异概率增加不同天线之间卫星序列交流的方法并不可取。这意味着，每个天线安排的测控任务数量很大程度上由初始化过程随即决定。如果一些天线在初始化时拥挤度较高，则在整个优化过程中始终保持着高拥挤度，各个任务之间容易发生冲突。

为了解决单纯遗传算法存在的问题，提出了基于拥挤度的邻域生成策略，如图6 所示。该方法将拥挤度高的天线上安排的测控任务分配给拥挤度低的天线，以减少冲突。将天线的卫星序列长度定义为该天线的拥挤度ci(1 ≤i≤m)为每个天线上安排的任务数量。邻域生成的过程如下。首先，计算所有天线的拥挤度。然后，以拥挤度的值构造轮盘，抽取代替换的高拥挤度天线ai(1 ≤i≤m)。其次，以拥挤度倒数的值构造轮盘，抽取低拥挤度的天线基因aj(1 ≤j≤m)。最后，用aj代替ai。基于拥挤度的邻域生成策略意味着低拥挤度的天线容易作为补位天线，使各个测站之间的拥挤度尽量平均。基于拥挤度的模拟退火过程如图7所示。在遗传算法每一代进化完成以后，从种群中抽取适应度最高的部分个体进行模拟退火。首先，对于抽取的每一个个体，设置模拟退火初始温度η0。然后，采取基于拥挤度的邻域生成策略生成扰动解，计算扰动解和原解适应度的差。如果扰动解更优，则接受扰动解，如果原始解更优，则按照Metropolis 准则判断是否接受扰动解。逐步降温，重复以上过程，直至达到结束温度。最后，将经过模拟退火的染色体放回原种群。

图6 基于拥挤度的邻域生成策略Fig.6 Congestion-based neighborhood generation method

图7 基于拥挤度的模拟退火流程Fig.7 Diagram of congestion-based simulated annealing

2.5 基于拥挤度的SA-GA完整算法流程

综合2.1 至2.4 节内容，形成的混合模拟退火遗传算法的完整流程如图8 所示。第一步，设置遗传算法和模拟退火参数，并初始化种群。第二步，对种群中所有个体进行解码并计算适应度。第三步，轮盘赌方法选择子代个体，并进行选择、交叉、变异的遗传操作，生成子代种群。第四步，基于拥挤度对适应度最高的部分个体进行模拟退火，结束后放回子代种群。不断重复迭代上述过程，直至达到最大遗传代数。输出最优解并结束算法。

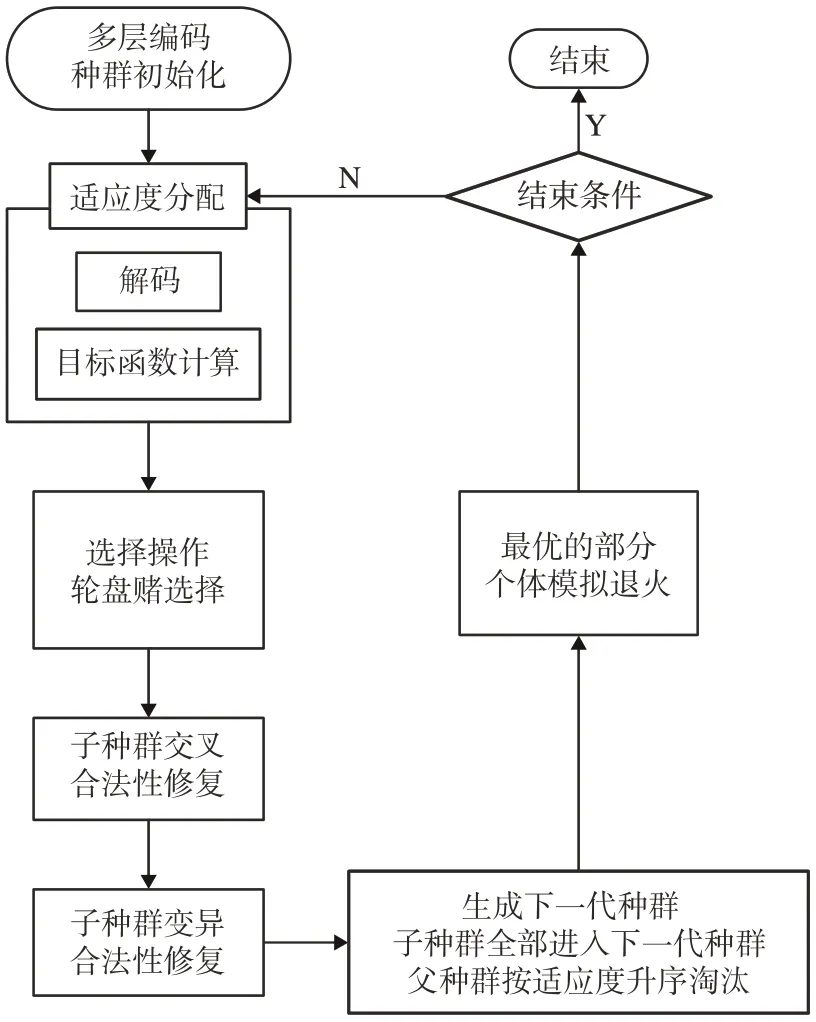
图8 基于拥挤度的混合模拟退火遗传算法协调逻辑Fig.8 Diagram of HSAGA based on congestion

3 工程应用结果与分析

为了验证算法的可行性与高效性，下面进行了单纯遗传算法和混合模拟退火遗传算法的算法对比实验。算法实验在真实卫星和地面站系统的数据库上进行。共有卫星180颗，地面站天线32，任务规划周期为24 小时，每颗卫星安排2 到4 个不等的测控弧段。两种算法都取不同的参数进行了10 次仿真实验，各取最优结果。最优解情况下，单纯遗传算法参数设置：种群规模1 000，选择概率0.9，交叉概率0.8，变异概率0.5。混合模拟退火遗传算法的参数设置：种群规模500，选择概率0.9，交叉概率0.9，变异概率0.5，模拟退火比例0.01，初始温度1 × 108，结束温度1 × 103，降温速率0.1。

两种算法优化轨迹的对比关系如图9 所示，其中图9（a）为算法历代以来的最优个体的进化轨迹，图9（b）为每一代种群的平均水平的进化轨迹。分析图9（a）可以发现，在加入模拟退火操作之后，算法的收敛速度得到很大提升。混合模拟退火遗传算法在迭代到第50 代时，综合收益已经达到单纯遗传算法迭代500 代左右的水平，耗时缩短为原来的10%。并且，在达到最大遗传代数时，混合模拟退火遗传算法的综合收益也显著高于遗传算法，综合收益达到0.918，任务完成率达到99.7%。分析图9（b）可以发现，整个进化历程中，加入混合模拟退火操作显著提升了整个种群的表现。实验验证了混合模拟退火算法的可行性与高效性。

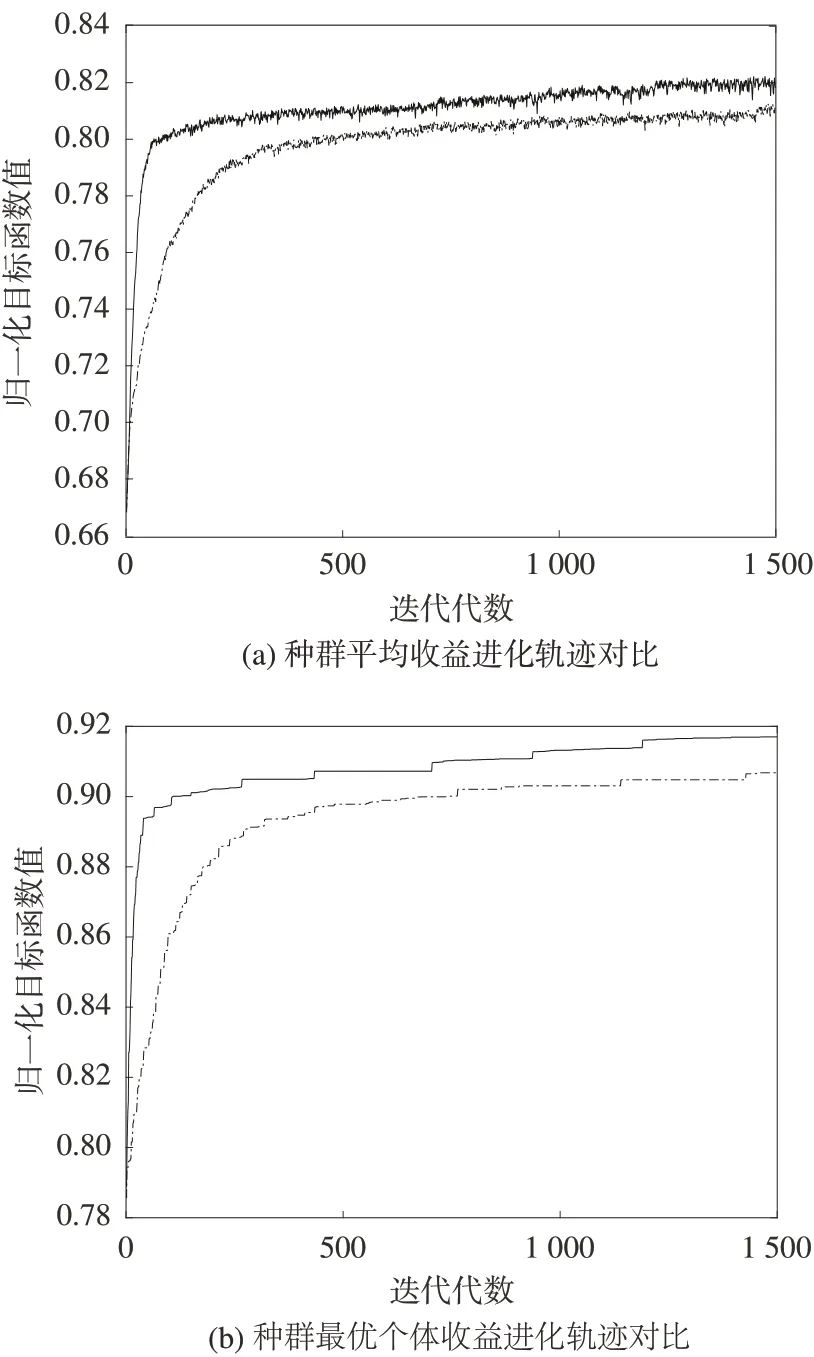
图9 算法对比试验进化轨迹Fig.9 Evolution trace of the algorithm comparison test

为了进一步验证在加入基于拥挤度的模拟退火操作之后星间任务分配是否变得更加均衡，将单纯遗传算法（GA）优化获得的最优结果方案与基于拥挤度的混合模拟退火遗传算法（SA-GA）计算得到的最优结果方案进行对比。

如图10 所示，图10（a）为没有加入基于拥挤度模拟退火操作时的各个天线上安排任务数量的分布情况，各个天线之间任务数量差异较大，图10（b）为加入了基于拥挤度模拟退火操作之后各个天线上安排任务数量的分布情况，各星上安排的任务数量分布在均值附近。将各个天线上安排任务数量的方差作为评价指标，如表2所示，在加入基于拥挤度的模拟退火操作之后，任务拥挤度方差降低为未加入该操作的47.81%。

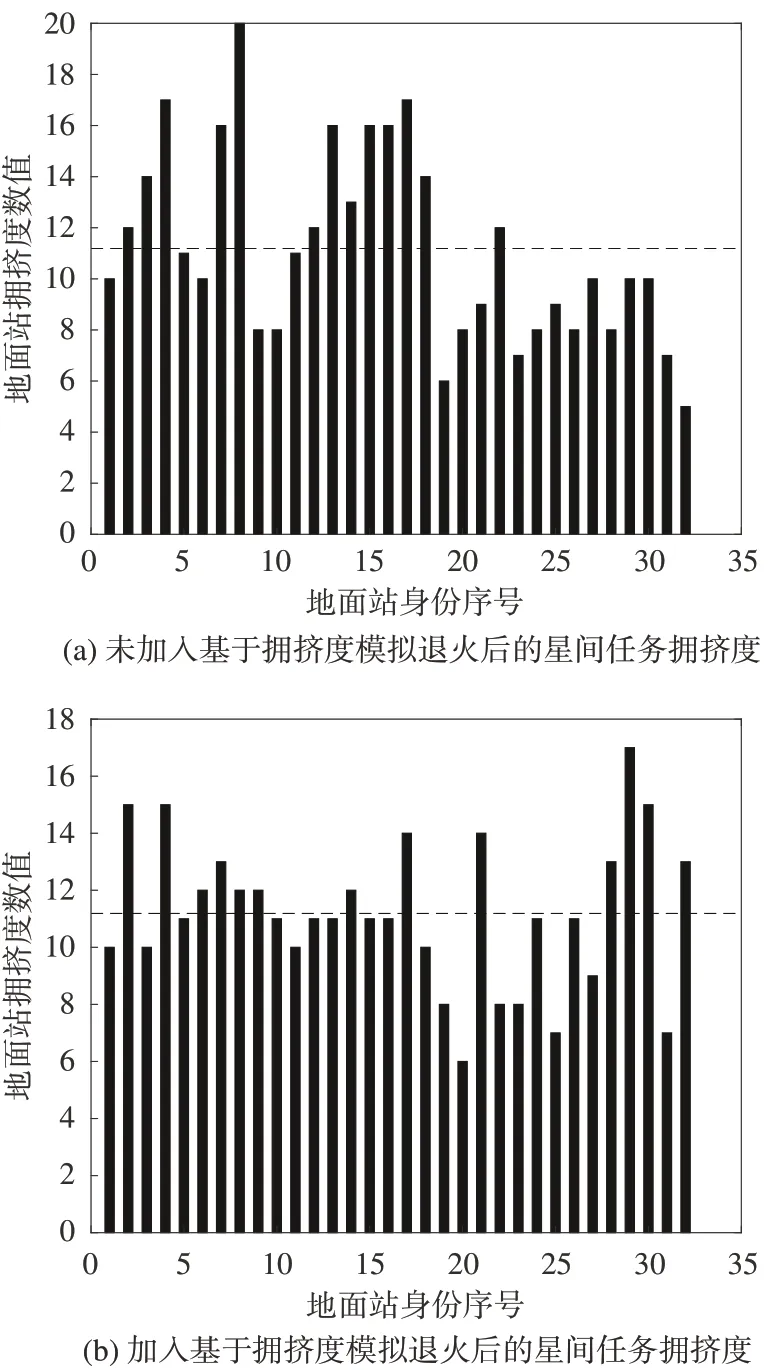
图10 加入基于拥挤度的模拟退火前后任务拥挤度对比Fig.10 Comparison of congestion before and after incorporation of congestion-based simulated annealing

表2 GA和HSAGA任务拥挤度方差对比Table 2 Congestion deviation comparison between GA and HSAGA

4 结论

为了解决大型星座的测控调度问题，建立了大型星座多星测控任务规划约束满足模型。采用多层编码方法实现多星、多测控天线测控任务分配编码。通过对多层编码遗传算法中算子特性的分析，提出了基于拥挤度的模拟退火操作方法，弥补了单纯遗传算法天线拥挤度高的问题，提高了算法效率。通过算法对比实验验证了混合模拟退火遗传算法的有效性和高效性。具体表现为：算法耗时减少为单纯遗传算法的10%；任务完成率达到99.7%；综合收益达到0.918，显著高于单纯遗传算法。并且，在加入基于拥挤度的混合模拟退火之后，各个天线的任务拥挤度均衡性显著改善，加入该操作后，天线间任务数量方差降低为未加入该操作时的47.81%。