加速非定常影响下跨介质飞行器终端滑模控制
2023-12-28张梓晨荣思远王小刚白瑜亮崔乃刚
张梓晨,荣思远,王小刚,白瑜亮,崔乃刚
(哈尔滨工业大学航天学院,哈尔滨 150001)
0 引言
随着跨介质飞行器的发展及各国之间的竞争愈演愈烈,对飞行器速度提出了更高需求。超空泡技术能够使得跨介质飞行器入水过程的阻力极大降低,引起了国内外学者的广泛关注。由于部分被空泡包裹,高速跨介质飞行器所受到的流体动力与传统的飞行器有极大的差别,空泡与飞行器间的复杂耦合关系、浮力大幅减小、非光滑非连续尾拍力等的存在使得跨介质飞行器具有强时变、强非线性的特点,给其控制系统设计带来了极大挑战[1]。
目前国内外有关超空泡问题的研究大都针对其巡航阶段。Dzielski等[2]建立了超空泡航行体的基准数学模型,并设计了线性反馈控制律。文献[3]针对超空泡航行体的分叉行为进行了分析,研究了系统稳定性与空化数相关的分叉行为,并设计了动态线性反馈控制律。Mao 等[4-5]针对尾舵沾湿率不确定性问题开展了研究,基于超空泡航行体的时滞模型,设计了鲁棒自适应反演控制器。文献[6]建立了超空泡航行体的串级系统,采用反步控制方法,设计了具有抗扰特性的H∞鲁棒控制器。张成举等[7]针对超空泡航行体运动过程中环境噪声和测量噪声带来的不利影响,提出一种基于无迹卡尔曼滤波器的最优控制算法。文献[8]通过分析滑行力的时滞特性,基于超空泡航行体的线性参数变化时滞模型,设计了一种基于时滞特性的预测控制器。文献[9]中针对超空泡航行体巡航段深度控制问题,设计了分数阶滑模控制器,提高了收敛速度,同时确保系统平滑收敛。文献[10]提出了一种基于扰动观测器的边界滑模控制方法,通过估计非线性滑行力的边界以降低滑模控制器的开关增益。Wang 等[11]针对具有不确定性的超空泡航行体系统,设计了一种基于RBF 扰动观测器的自适应滑模控制策略,通过RBF 神经网络权值更新策略实现了对扰动的准确估计,保证了轨迹跟踪误差的收敛。
部分学者也针对非全包裹阶段以及加速过程开展了相关研究。文献[12]中对于非全包裹超空泡航行体的控制系统进行了深入研究,针对尾部压差经验值效率不确定问题,设计了自适应反演变结构控制器。Kim等[13]针对通气超空泡航行体加速段流体动力特性进行了研究,并耦合考虑通气率与空化数之间的关系进行了仿真分析。文献[14]针对超空泡航行体加速段控制问题,提出了一种基于神经网络的自适应控制方法,实现了具有系统不确定性条件下的深度跟踪控制。
终端滑模控制方法(Terminal sliding mode control,TSMC)是一种能够实现有限时间稳定性的滑模控制方法,该控制方法通过调节分数幂,提高了在平衡点的收敛速度,实现了误差信号的快速收敛,在各类控制问题中得到了广泛应用[15-18]。Wu 等[19]针对一类二阶非线性系统,设计了一种非奇异终端滑模控制方法(Non-singular terminal sliding mode control,NTSMC),通过一个特定的基于小增益的不连续控制项保证了系统收敛,且对抖振有较好的抑制效果。文献[20]针对吸气式高超声速飞行器的控制问题,提出了一种自适应终端滑模控制算法,通过将自身状态的放缩引入到高阶滑模算法中,提高了系统响应速度。
空泡摄动、建模不确定性以及外界扰动的影响给跨介质飞行器控制系统设计带来了很大的挑战,目前研究中,针对这些复杂干扰一般采用扰动观测器的方法进行处理[21-23],即通过反馈的状态量信息,对其导数信息进行求取,耦合考虑所建立的系统状态方程,得到对扰动的精确估计,并在控制系统中进行反馈,以提高系统控制精度和鲁棒性。在文献[24]中,针对一类非线性不确定系统,构造了一种多变量线性扩张状态观测器,并采用频域分析方法剖析了不确定动态估计的收敛性。Ali 等[25]设计了一种基于比例积分速度变量的三阶快速有限时间扩张状态观测器(Finite-time extended state observer,FTESO)来估计系统的集总扰动,并证明了观测器的有限时间一致有界性。Michael 等[26-27]利用基于非递归和递归算法的高阶滑模(High order sliding mode,HOSM)观测器,讨论了观测器的有限时间收敛特性。
综合上述文献可知,目前有关跨介质飞行器巡航段的控制研究很多,但均未考虑加速非定常流体动力的影响。本文重点针对扰动作用下的含有加速非定常影响的跨介质飞行器控制问题进行研究。首先设计空泡通气规律,得到空泡演化模型,进而计算飞行器沾湿区域流体动力,得到加速段数学模型。基于误差模型设计有限时间收敛状态观测器,对系统的集总扰动进行观测补偿,并设计非奇异快速收敛终端滑模面,结合高阶滑模趋近律完成控制器设计。基于Lyapunov 理论证明控制系统的稳定性,最后通过数学仿真验证控制系统的鲁棒性和控制精度。
1 跨介质飞行器加速段纵向数学模型
1.1 飞行器受力分析
本文主要针对跨介质飞行器从全湿流状态至完全被空泡包裹的超空泡状态的加速阶段的纵向平面运动进行控制器设计,在进行受力分析及推导动力学模型前,先进行如下基本假设。
1)跨介质飞行器为理想刚体且质量与质心位置保持恒定,在运动过程中不产生变化;
2)跨介质飞行器为对称回转体,本文仅考虑其在纵平面受力及运动的影响,假设无横滚,无侧向受力,且偏航角及角速度、横滚角及角速度、侧滑角等参数在飞行器运动过程中均保持为零。
跨介质飞行器的配置如图1 所示,前端为圆盘空化器,用于诱导产生空泡并提供升力和控制力,飞行器主体部分为锥柱结合的对称回转体,尾部有4片尾舵进行控制。
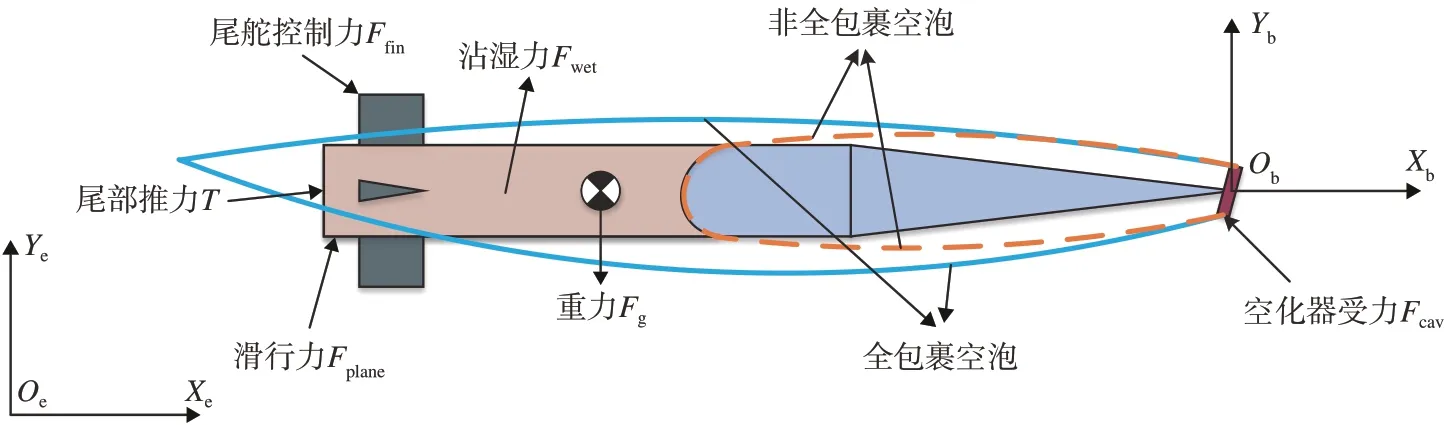
图1 跨介质飞行器受力示意图Fig.1 Forces on the trans-media aircraft
跨介质飞行器在运动过程中所受流体动力很大程度上受到空泡形态的影响,当飞行器速度较低时,空泡仅将飞行器部分包裹,大部分处于沾湿状态,如图1中虚线所示。此时飞行器受到空化器作用力、尾舵作用力、重力、沿体轴方向的推力以及沾湿部分流体动力的影响。当飞行器加速至一定速度时,空泡将飞行器全部包裹,如图1中实线所示,此时飞行器受到空化器作用力、尾舵作用力、重力、推力以及因尾部穿出空泡而受到的滑行力的影响。
针对飞行器受到的各种力的作用,在弹体系下进行建模,弹体坐标系原点在空化器中心,ObXb轴沿飞行器纵轴方向指向前方,ObYb轴与ObXb轴垂直,当飞行器在地面正常放置时指向上方。
1.2 各部分流体动力计算
1.2.1 空化器和尾舵作用力
本文中,圆盘空化器的受力方式如图2所示,其受力可分解为升力和阻力,计算方式如下。
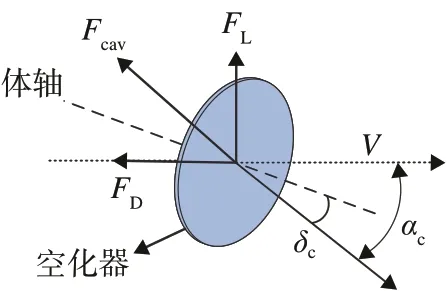
图2 空化器受力Fig.2 Forces on the cavitator
式中:ρ为水的密度;V为跨介质飞行器速度;Cx0为零空化数下阻力系数,通常取Cx0=0.82;Rn为空化器半径为空化器攻角;σ为空化数,为空泡形态方程的特征参数,其表达式为
式中:p∞=-ρgye为飞行器当前深度水的静压;pc为水的饱和蒸汽压,常温下取pc=3 540 Pa。
通过在体轴进行分解,空化器在沿体轴ObXb方向上的受力可写为
同理可知在体轴ObYb方向上的力为
尾舵可看做一种特殊楔形的空化器,根据空化器作用力,可给出尾舵作用力为
式中:n为尾舵与空化器相似系数,一般取n=0.5;为尾舵处攻角;δf为尾舵舵偏角;I(t)为尾舵沾湿率,用于表征尾舵被空泡包裹后的控制效率,当空泡形态变化时,尾舵沾湿率也随之变化。不同空泡形态下尾舵沾湿示意图如图3所示。
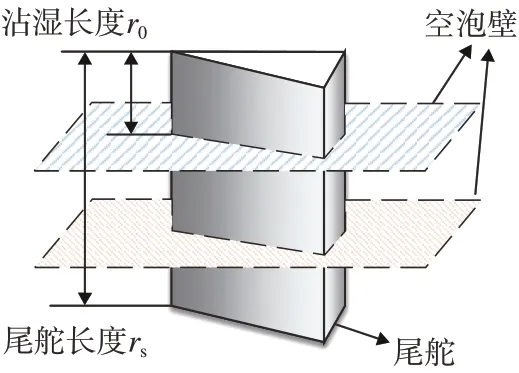
图3 尾舵沾湿示意图Fig.3 Scheme of fin immersion
考虑几何关系,尾舵沾湿率的计算方式如下:
式中:r0为尾舵沾湿长度;rs为尾舵长度;Rc为尾舵处空泡半径。
1.2.2 沾湿部分作用力
沾湿部分作用力由浮力FB以及沾湿部分流体动力Fh组成,其受力示意图如图4所示。
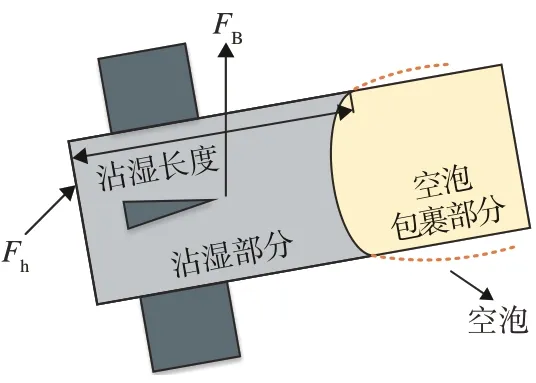
图4 沾湿部分受力Fig.4 Forces on the wetting part
浮力大小与沾湿长度Lwet成正比,且浮力矩作用点为沾湿部分的中心,故浮力及力矩表达式为
沾湿部分除浮力外还会受到流体动力作用,其表达式为
式中:Chx,Chy分别为流体动力阻力和升力系数。
当跨介质飞行器加速至较高速度时,空泡将飞行器全部包裹,此时沾湿长度Lwet=0,不再受到浮力以及流体动力的影响。
1.2.3 尾部滑行力
尾部滑行力是由于飞行器尾部与穿出空泡壁产生的流体动力,根据Hassan 圆柱体滑行力计算公式,可知滑行力计算公式为
式中:h′为归一化后飞行器尾部沾湿深度;αp为沾湿处攻角,其计算公式如下:
1.2.4 重力及推力
在本文中对模型进行简化,不考虑燃料消耗对重力大小及质心位置的影响,将地面系下的重力在弹体系进行分解可得重力的表达式为
式中:g为重力加速度;xc为质心到空化器中心的距离。
推力简化为沿体轴的常值推力,且其作用点在跨介质飞行器中心线上,即推力产生的力矩为零,其表达式为
结合运动学与动力学模型,可得最终跨介质飞行器的数学模型为
2 通气规律设计及空泡形态分析
跨介质飞行器在加速运动过程中,空泡形态对其流体作用影响极大,为了使得空泡快速稳定膨胀,同时也为了削弱自然空化的不确定性,在跨介质飞行器运动过程中采用通气的方式来使其稳定。
本节对跨介质飞行器加速段空泡形态开展分析,基于经典空泡模型,根据通气空泡的不稳定性上界设计通气规律,并进行仿真分析。
2.1 空泡形态方程
目前有关超空泡的研究中,通常假设空泡呈轴对称的椭球形,且每个截面看作一个圆形,其形态如图5所示。
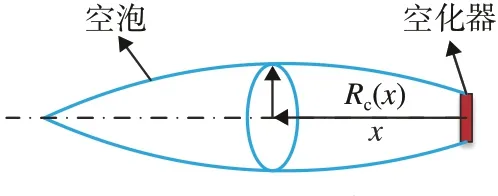
图5 空泡形态Fig.5 The shape of cavity
根据Logvinovich 空泡模型,可知在每个截面x处的空泡半径Rc以及对应的为
式中:Rn为空化器半径;Rk为空泡最大半径;τ为修正系数,一般取τ=0.85。空泡轮廓在0 时刻半径为Rn,经过t时间空泡半径为Rc,空泡半径变化率为,从0 时刻经过tk时间空化器移动到空泡半长,根据椭球形的形态假设,此时空泡具有最大半径。
空泡最大半径Rk和空泡的半长Lk为
2.2 通气规律设计
考虑到自然空化的不稳定性,通过设计通气规律可获得一个适宜的通气量变化规律,使得跨介质飞行器快速且稳定的达到超空泡包裹阶段。
一般来说通气量越大,空泡生长的速度越快,但相关试验表明,当通气流量大到一定值时,空泡的稳定性就会丧失,如图6 所示,此时空泡成脉动状,并周期性的发生气体外泄。
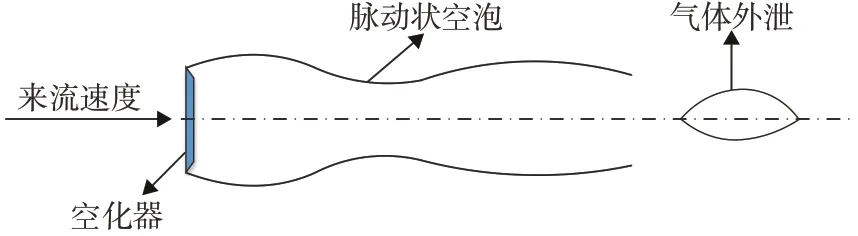
图6 通气空泡的不稳定性Fig.6 Instability of ventilated cavity
研究表明,通气空泡的不稳定性主要依赖于通气空化数于自然空化数的比值:
式中:σv为自然空化数;σg为通气空化数。
通气空泡的σg通常小于σv,即β0≥1,随着β0增大,通入空泡中弹性气体的作用增加,当β0>2.645 后,通气空泡不稳定。故考虑通气空泡的不稳定特性,设计通气空化数为
式中:σc为所设计的理想空化数。
根据上述通气规律以及空泡形态方程,对比分析自然空化和采用本文通气规律下的空化数和飞行器沾湿长度变化,速度范围V=30~100 m∕s,参考深度为水下4 m。
如图7所示,在通气条件下,空化数有了显著的降低,根据空泡形态方程,其空泡形态更大,通气条件下跨介质飞行器沾湿长度更小,其所受到的阻力更小,更有利于加速,且在V=56.29 m∕s时即可实现空泡对飞行器的全包裹,而自然空化在V=91.54 m∕s时才达到全包裹阶段。
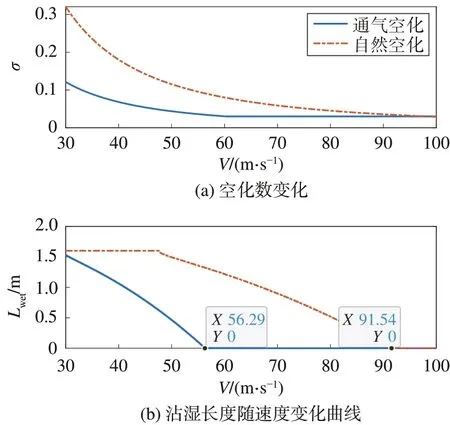
图7 空化数及沾湿长度随速度变化曲线Fig.7 Cavitation number and wetted length curves with velocity
针对通气条件下开展空泡形态分析,当σ=0.034 4 时,即可实现空泡对飞行器的全包裹,此时沾湿长度刚好为零,但由于此时飞行器尾部与空泡壁距离较近,易出现尾拍现象,不利于跨介质飞行器稳定,空泡形态如图8 所示,而当空化数较小时,空泡形态过大,将尾舵全部包裹,控制效率过低,故设计理想空化数为σc=0.030 0,此时尾部与空泡壁有一定间隙,且尾舵也有大部分沾湿。
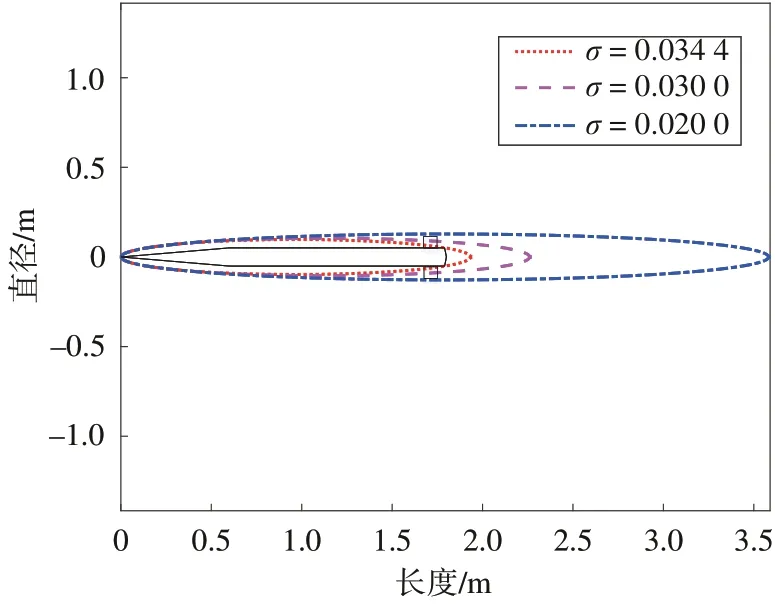
图8 空泡与飞行器相对关系Fig.8 The relative relationship between cavity and the aircraft
3 基于有限时间观测器的终端滑模控制器设计
本节基于上文中跨介质飞行器考虑水下加速段的建模以及加速过程中通气规律的设计,对控制导向模型进行了推导,并设计了基于有限时间扰动观测器的跨介质飞行器非奇异终端滑模控制器。
由图9 系统框图可知,首先基于误差信号及其导数信息设计非奇异终端滑模面,然后基于滑模面设计等效控制律及高阶滑模形式的趋近律。针对控制系统中存在的复杂扰动,引入有限时间收敛状态观测器对系统不确定性进行观测补偿,实现跨介质飞行器在加速段的高精度稳定控制。
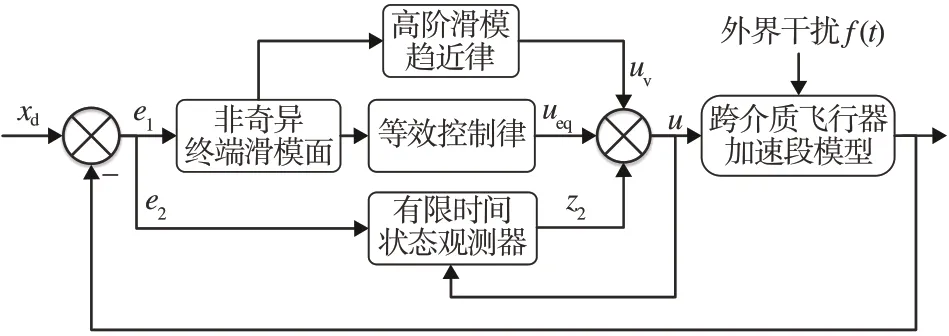
图9 跨介质飞行器加速段控制系统框图Fig.9 Trans-media aircraft transition phase control system
3.1 跨介质飞行器控制模型
为了便于控制器设计,首先基于跨介质飞行器动力学方程进行简化,将其改写为便于控制器设计的模型。
首先令x1=[ye,θ]T,x2=[vy,wz]T表示状态量,令u=[δc,δf]T,为了便于公式推导,令:
考虑到几何关系,当对深度指令以及俯仰角指令进行跟踪控制时,垂向速度以及俯仰角速度需要满足,则各状态量的误差形式定义为
在跨介质飞行器的加速及后续运动的控制过程中,会出现系统建模误差、空泡摄动引起的沾湿流体动力、尾舵沾湿率计算不准确以及外界干扰等不确定性,令f(t)为系统集总扰动,则式(22)改写为
3.2 有限时间收敛扩张状态观测器
首先给出如下引理:
引理1.[29]考虑以下非线性系统:
假设原点为系统的一个稳定平衡点,且存在连续可微正定函数V(x):Rn→R+∪{0},实数k>0及α∈(0,1),在包含原点的开邻域内满足:
则系统在原点处有限时间收敛,且从初始状态收敛到原点的时间T(x0)上界满足:
为了提高系统控制精度,设计有限时间收敛状态观测器对跨介质飞行器控制系统的集总扰动进行观测,在设计观测器之前,首先考虑式(27)所示系统:
式中:sig(x,α)=|x|αsgn(x),sgn(·)为符号函数。幂次 序 列αi(i=1,2,3)设 计 为αi∈(0,1)(i=1,2,3)且满足αi=iα-(i-1),其中α在区间(1 -ε,1)内,ε为一个足够小的正数。L>1 为放大因子,矩阵Aα满足Hurwitz条件:
根据上述条件给出以下稳定性定理:
定理1.当系统中的幂次序列按照设计要求给出,则系统可在有限时间内收敛到原点的邻域内,且收敛时间的上界满足:
证:首先进行坐标变换:
则系统可转换为
令d=[d1,d2,d3]T,且可知系统和具有相同的收敛时间。
构造关于系统的Lyapunov函数:
因增益系数矩阵Aα满足Hurwitz 条件,故存在正定对称矩阵Pα和正定矩阵Qα,使得:
所以式(32)的全导数为
根据加权齐次性的定义[30],当对状态量di选择相同的权重αi时,V1(ξ)和具有关于相同权值向量αε=的加权齐次性,且其齐次度分别为1 和,则存在常数c,使得下列不等式恒成立[31]:
再考虑函数(32),根据瑞利不等式可知:
又因为式(31)右侧关于α连续,则有:
根据引理1,可知系统(31)可在有限时间内收敛,且收敛时间上界为
又系统(27)和(31)具有相同的收敛时间,定理1证毕。
根据定理1中的内容,针对式(23)所示的二阶系统,设计具有模型参考的状态观测器为
当系统(40)收敛时,有z1=e2,z2=f,定义观测误差为
将式(23)和(40)代入式(41)中可得状态观测器的误差表达形式为
由定理1可得,当t>Tob时,i=1,2,3可收敛至原点的邻域内,即z1→e2,z2→f。
3.3 快速终端滑模控制律设计及稳定性证明
针对传统终端滑模控制器中存在的抖振及奇异的问题,基于误差信号的高阶导数,设计一种非奇异终端滑模控制器,可以有效的抑制抖振现象,定义终端形式的滑模面为
式中:p,q为正定的控制增益系数矩阵;γ1,γ2均为奇数,且满足
引理2.[32]假设一个正定的Lyapunov 函数V(x),其全导数满足,其中α,β>0,且p1∈(0,1),x可在有限时间内收敛为零,收敛时间上界为
定理2.设计滑模面形式为时,当滑模面s为零后,系统状态x可在有限时间内收敛为零。证:滑模面收敛为零后有
由引理2 可知定理2 得证,即滑模面收敛为零后,系统状态误差可在有限时间收敛为零。
完成滑模面的设计后,可将控制量分为在滑模面上运动的等效控制量ueq、趋近滑模面运动的趋近控制量uv以及上一节中扰动观测器的输出z2,根据误差动力学模型,设计非线性控制律:
式中:ueq为等效控制项;uv为趋近运动控制项;u为输出的实际控制量。
根据滑模面,设计等效控制项ueq为
对于趋近运动控制项,为了使得滑模面能够平滑稳定达到稳定状态,设计以下含有高阶滑模形式的趋近运动控制项:
根据定理1 可知,存在固定时间tob和一个小的常数N,满足当t>tob时,有‖f-z2‖≤N。故当选取ξ>N时,继续推导式(54)可得:
故根据引理1 可知系统将在有限时间内收敛到零,即滑模面s=0,根据定理2 可知,在滑模面收敛为零后,系统误差e1可在有限时间收敛为零。
注1.为了进一步抑制抖振效应,可采用饱和函数sat(s)来替代符号函数sgn(s)。
4 仿真结果分析
根据上文所述的有限时间收敛状态观测器及非奇异终端滑模控制方法,对加速段非定常影响下的跨介质飞行器控制进行仿真分析,采用的参数见表1。

表1 跨介质飞行器系统参数Table 1 System parameters of Trans-media Aircraft
针对上述设计的控制器及扰动观测器进行仿真分析,为了体现出本文所提出的有限时间扰动观测器(FTESO)及非奇异终端滑模控制算法(NTSMC)的优越性,设计传统滑模及扩张状态观测器进行对比仿真分析,设计对比工况为采用传统滑模控制方法(SMC)及线性扩张状态观测器(LESO)。
其中,线性滑模面和趋近律为
设计控制算法为
线性扩张状态观测器设计为
非奇异终端滑模控制参数设计为p=[2,-75;0,2 ],q=1.5I2×2,η0=120,η1=0.5,η2=0.7,ξ=0.1,r1=7,γ2=5,舵偏角限幅为-30°≤δc,δf≤30°。扰动观测器参数为α=0.8,L=5,k1=31,k2=311,k3=1001。对比工况中,线性扩张状态观测器参数设计为L1=31,L2=311,L3=1 001,传统滑模控制律参数设计为k=[2,-vx;0,2],η=120I2×2,D=3。
设定深度控制指令为yd=-4 m,俯仰角指令为θd=0°,初始速度为vx=30 m∕s,初始深度y0=-1 m,其余初始条件皆设置为零,并且为了验证和对比分析所设计的控制算法及状态观测器的性能,针对复杂扰动下开展仿真分析,给定扰动为
具体仿真结果如图10~12所示。
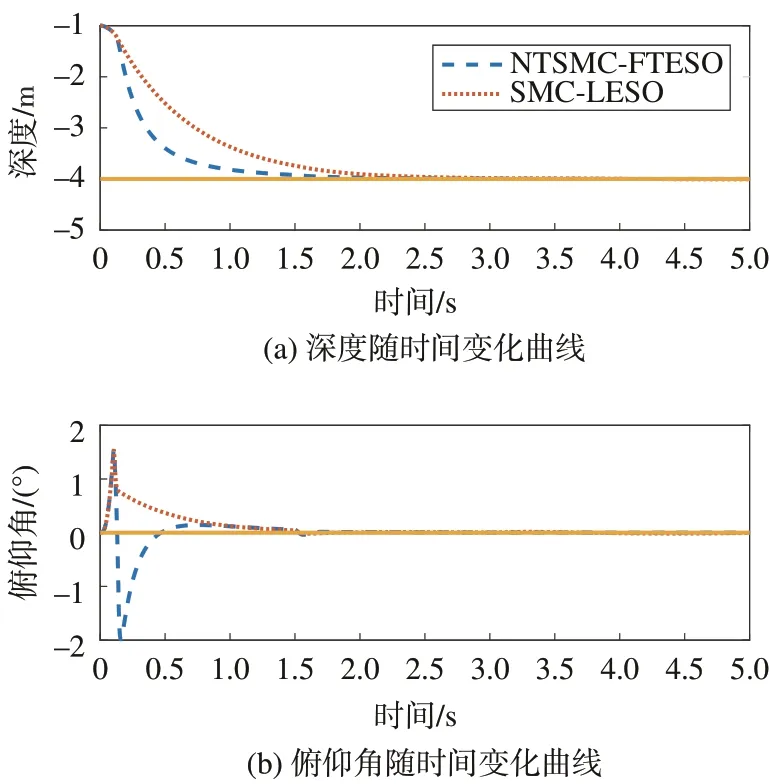
图10 深度及俯仰角随时间变化曲线Fig.10 Depth and pitch angle responses over time
从图10 所示的深度及俯仰角响应曲线可知,在复杂扰动作用下,本文所设计控制方法依然可以实现对控制指令的快速响应,且相较于传统滑模算法具有更快的收敛速度和更好的控制精度。
从图11 控制指令曲线可知,本文所设计的非奇异终端滑模控制算法很好的抑制了抖振效应,实现了控制指令的平滑输出。从图12 状态观测器可以看出,在复杂扰动影响下,采用本文的有限时间状态观测器能够在0.3 s 内实现对扰动的精确观测,并且可对扰动进行持续精确观测,而对比工况中的线性扩张状态观测器则需要0.7 s 才能收敛,且当扰动变化时,观测精度有所下降。
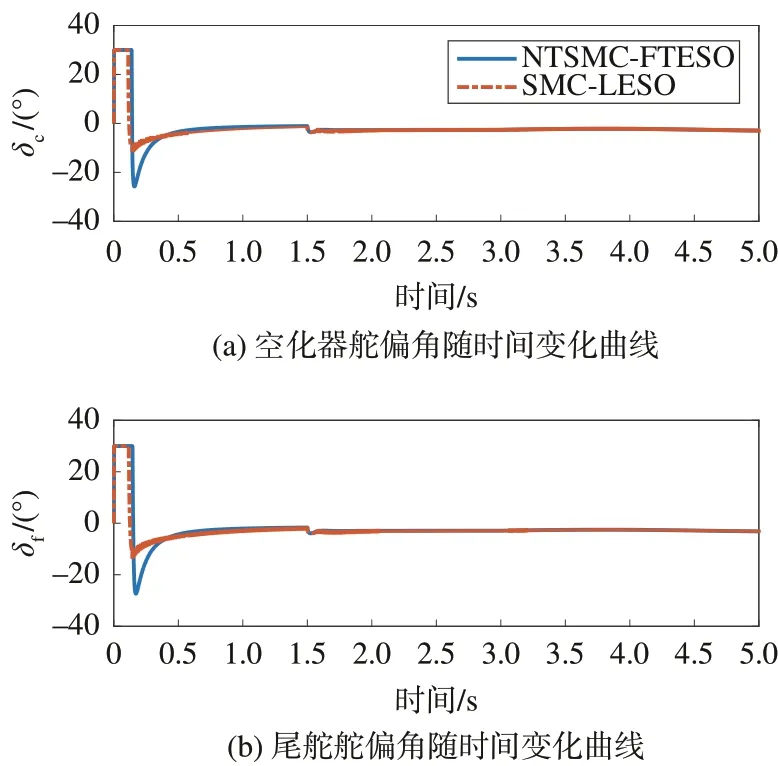
图11 控制指令随时间变化曲线Fig.11 Control inputs over time
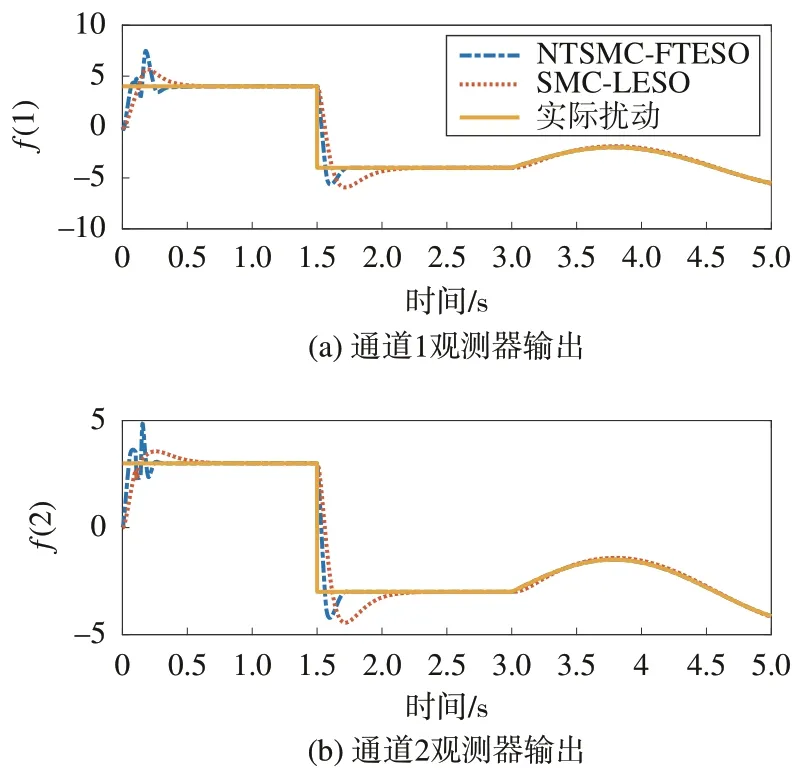
图12 状态观测器输出结果Fig.12 Outputs of state observer
5 结论
1)本文针对加速段非定常影响下的跨介质飞行器控制问题,设计了基于有限时间收敛状态观测器的非奇异终端滑模控制器。状态观测器可实现对复杂扰动的快速高精度估计,并且在控制系统中进行补偿,增强了系统稳定性,提高了控制精度;非奇异终端滑模控制算法能够在保证快速收敛的前提下实现对控制信号的高精度跟踪,同时能够抑制滑模控制算法中的抖振效应。
2)本文设计的控制算法所需设计的控制增益参数较多,参数整定难度较大,并且未考虑执行机构饱和对控制器带来的影响,在后续的工作中,会针对抗饱和控制问题开展进一步研究。
