光学卫星等比降地速的地影区主动推扫姿态规划

童鑫，钟 兴，曲友阳，李文涛，李冬瑞

（长光卫星技术股份有限公司，长春 130102）

0 引言

光学推扫卫星在自然资源调查、农业管理、林业管理、环境监测与城市规划等方面发挥着重要的作用［1］，其多采用具有灵敏度高、动态范围宽等优点的时间延迟积分电荷耦合器件（TDI-CCD）作为传感器［2-3］，利用CCD 中同一列的多个像元对同一目标进行连续曝光，采用多级积分技术来增强信号强度和信噪比［4-6］。光学推扫卫星的成像模式主要包括被动推扫成像与主动推扫成像［7-8］。被动推扫成像是指成像过程中卫星本体坐标系相对轨道坐标系保持固定的姿态角，依靠被动地速进行推扫成像，相机成像区域的轨迹与卫星的星下点轨迹平行。现有部分光学推扫卫星因姿态机动能力不足普遍采用被动推扫成像模式，如中国的高分七号卫星、资源三号卫星、欧空局Sentinel-2A 卫星与日本的ALOS 卫星。随着卫星技术的快速发展，卫星姿态机动能力得到显著提高。卫星在面对河流、海岸线与公路等特定区域的成像任务时，成像期间姿态固定的被动推扫成像模式已无法满足需求，因此，主动推扫成像模式应运而生。主动推扫成像是指成像过程中利用卫星的快速机动能力，通过姿态规划使卫星实时以期望角度与期望角速度进行姿态的不断调整，使得卫星相机实现对特定区域目标的推扫成像［9］。目前，具有主动推扫成像模式的卫星有中国的新技术试验卫星、高分多模卫星、北京三号卫星与吉林一号高分04A 卫星等，以及法国的Pleiades 系列卫星与SPOT-6∕7 卫星、美国的Worldview 系列卫星与GeoEye-1 卫星。同时，国内外学者也在开展关于主动推扫姿态规划相关的研究［10-15］。文献［10］对卫星一轨内多个条带目标的成像时序问题进行规划，通过建立成像开始时刻的规划模型，使用序列二次规划算法对规划模型进行求解。该方法可满足任意走向条带目标的主动推扫成像观测需求。文献［11］通过迭代拟合建立目标位置的六阶或七阶多项式模型，并基于所得模型计算目标跟踪所需的侧摆角、俯仰角以及图像运动补偿的偏航角。该方法能够有效解决沿海岸线、边界线、河流等曲线目标的主动推扫姿态规划问题。文献［12］通过拟合轨迹方程以优化可检测目标数量的方法，实时求解卫星的三轴姿态，使TDI成像速度与轨迹方向一致，可高效地沿着曲线分布的目标进行扫描。文献［13-14］针对常规推扫成像方法无法满足超大幅宽成像的需求，提出了一种卫星快速旋转超大幅宽的主动摆扫成像方法，解决了单个卫星相邻两轨成像区域之间的无缝拼接成像问题。文献［15］针对沿海地带目标区域通常存在非线性弯曲分布的情况，基于海岸带特征点的位置计算了当卫星光轴始终指向特征点时的姿态，并建立了考虑时变卫星姿态和动态扫描摆动镜头的速度向量模型，可以实现沿海目标主动推扫成像。此外，针对卫星主动推扫成像期间偏流角计算方法的研究工作也已开展［16-17］。

目前的主动推扫姿态规划方法主要针对卫星在阳照区的非沿迹目标成像的姿态指向问题，缺乏对地影区进行主动推扫成像的姿态规划方法，限制光学推扫卫星用于地影区成像的主要因素是成像区域的地速。光学推扫卫星被动推扫成像时，成像区域的地速主要受卫星飞行速度与该区域地球自转速度所影响，成像区域在像面上的像移速度与成像区域的地速存在一定的正比例关系。卫星相机TDI-CCD的行转移时间与积分时间的设计值与像移速度是匹配的，当光学卫星在地影区进行被动推扫成像时，成像区域的光源主要是城市灯光、森林火灾与火山爆发等产生的较弱亮光与黑暗背景，用于阳照区的积分时间相对过小而难以获取高质量影像所需的足够高的信噪比。因此，常规光学推扫卫星难以用于在地影区进行夜光成像，而夜光遥感数据在灾害监测、生态环境评估、社会经济评估与人口评估等方面发挥着越来越重要的作用［18］，通常只能依靠携带专业夜光传感器或仪器的夜光遥感卫星获取夜光遥感影像，如搭载可见光成像线性扫描业务系统（OLS）的美国国防气象卫星、搭载可见光近红外成像辐射仪（VIIRS）的美国国家极轨卫星、搭载高灵敏度平面阵列CMOS夜光相机的武汉大学珞珈一号卫星与通过面阵传感器凝视成像模式获取夜光影像的吉林一号视频系列卫星等。

针对光学推扫卫星在地影区进行成像的应用场景，本文设计了一种等比降地速主动推扫姿态规划方法，可用于光学推扫卫星在地影区进行夜光成像。根据卫星推扫成像任务的姿态机动时间、降速比例等信息计算出轨道递推时间与轨道递推后的地面等比降地速点的坐标，进而反算出卫星实时姿态。该姿态规划方法可使相机成像区域的地速等比例降至被动推扫模式地速的任意比例，通过降低成像区域地速的方式降低了成像区域在像面的像移速度，进而增大了TDI-CCD 的行转移时间与积分时间。基于吉林一号高分04A卫星参数对所设计的姿态规划方法进行了数值仿真并进行了卫星的在轨试验，结果证明了该方法的可行性与有效性。

1 卫星推扫任务姿态规划

本文使用了若干个航天飞行器常用坐标系，包括轨道坐标系Fo(Oo-XoYoZo)、地球固连坐标系（WGS-84 坐标系）Fe(Oe-XeYeZe)、地心惯性坐标系（J2000 坐标系）Fi(Oi-XiYiZi)与卫星本体坐标系Fb(Ob-XbYbZb)，以上各坐标系的定义参见文献［19］。

1.1 被动推扫任务姿态规划

被动推扫任务卫星只需要在每个控制周期Tctrl内根据接收到的实时轨道信息与姿态信息，控制其在轨道系下的三轴姿态角达到期望值即可，通常情况下俯仰角θ为0°，侧摆角φ为任务上注值，偏航角ψ为根据成像区域地球自转速度与卫星飞行速度计算出来的偏流角补偿值。卫星进行被动推扫成像任务需要通过地面进行指令上注，规定卫星的成像开始时刻Tstart、成像结束时刻Tend、侧摆角φ与姿态机动开始时间Tmaneu，成像时长ΔT等于Tend-Tstart。被动推扫任务姿态规划分以下三个部分。

1）对地机动姿态规划

卫星非任务期间为帆板对日姿态，设在轨飞行中T时刻卫星的轨道为OT，若卫星接收到地面发送的推扫成像任务指令，当T等于Tmaneu时卫星开始进行成像姿态机动，在Tstart前卫星完成侧摆角φ、俯仰角θ与航向角ψ的姿态机动，保持侧摆角φ与俯仰角θ不变并实时为航向角ψ补偿偏流角直到Tstart时刻。

2）成像期间姿态规划

Tstart时刻相机开始加电进行成像，相机光轴在成像中心时刻Tcenter指向的地面点为Pcenter，Tcenter等于，成像期间卫星除Zb轴进行偏流角的实时调整外，其余两轴保持姿态不变。

3）对日机动姿态规划

当T等于Tend后被动推扫成像任务结束，卫星开始姿态机动使帆板对日，恢复长期在轨姿态。

被动推扫成像的整个姿态变化过程如图1 所示，其中Omaneu为卫星在Tmaneu时刻的轨道、Ostart为卫星在Tstart时刻的轨道、Oend为卫星在Tend时刻的轨道、Ocenter为卫星在Tcenter时刻的轨道、Pstart为卫星在Tstart时刻拍摄的地面目标点、Pend为卫星在Tend时刻拍摄的地面目标点。

1.2 等比降地速主动推扫姿态规划

光学卫星对地成像时，若已知卫星轨道与卫星姿态，则可根据地球椭球体模型直接解算出光轴指向地面目标点的坐标。若已知地面目标点坐标与卫星轨道，则可根据地球椭球体模型反算出卫星姿态。卫星若想实现降地速推扫姿态，则无法通过保持固定侧摆角与俯仰角的形式实现，因此，需要规划卫星的实时姿态。本文根据卫星在轨接收的成像任务中心点时刻，在确保对成像中心点附近成像时卫星姿态变化最小的情况下，通过轨道递推计算出地面目标点的起始点位置与等比降地速推扫的实时地面点位置，然后结合卫星的轨道位置反算出卫星姿态。所设计的等比降地速主动推扫任务姿态规划分以下四个部分。

1）初始地面目标点姿态规划

卫星非任务期间为帆板对日姿态，设在轨飞行中T时刻卫星的轨道为OT，卫星接收到地面发送的等比降地速推扫成像任务指令，其中降速比例为δ(0 ≤δ≤1)，其余任务参数与被动推扫任务相同。首先，根据任务参数对卫星轨道进行递推，根据地球椭球体模型与卫星侧摆角φ计算出第一个地面目标点的位置，然后再根据地球椭球体模型与卫星实时轨道位置反算初始姿态。

设第一个地面目标点对应的时刻为Tsol，其卫星轨道为Osol，为确保卫星对地面中心目标点附近成像时俯仰角变化最小，相机光轴在指向地面中心目标点Pcenter进行成像时卫星的俯仰角需要为0°。则相机光轴从地面目标点Psol移动到Pcenter的时间应与卫星从OT轨道位置移动到Ocenter轨道位置的时间相同，Tstart等几个时间需满足的关系如下：

Tsol确定后即可根据轨道递推计算出其对应的轨道位置Osol，再根据期望侧摆角φ计算出Tsol时刻相机光轴指向的地面目标点Psol，进而通过卫星实时轨道OT反算出卫星的初始姿态。

2）实时地面目标点姿态规划

初始轨道位置Osol确定后，为确保实现地面目标点的等比降地速，需要以Osol为起点在接下来的每个控制周期Tctrl内将轨道均递推δTctrl的时间间隔，得到递推的降速轨道Orecur，并实时计算出卫星在该位置处相机光轴指向的地面目标点Precur的坐标，进而通过Precur的坐标与卫星实时轨道OT反算出卫星的姿态。等比降地速推扫成像任务刚开始后，姿态机动前期相机光轴不能准确指向地面目标点Precur，但期望地面点Precur一直随着Orecur的递推而移动，当姿态机动完成后（姿态控制偏差满足控制指标），相机光轴即可一直跟踪Precur坐标的移动直至成像开始。

3）成像期间姿态规划

成像期间的姿态规划方法与实时地面目标点姿态规划方法相同，只需增加卫星Zb轴的偏流角调整。设卫星相机光轴在地面移动的平均速度为Vmean，因卫星进行了降速，实际成像期间的地面距离由被动推扫成像期间的VmeanΔT变为了δVmeanΔT。卫星相机在Tstart时刻加电，相机光轴拍摄的第一个地面目标点坐标不再是被动推扫姿态在Tstart时刻指向的Pstart，而是时刻对应的地面目标点的表达式为

当卫星飞行到Tcenter时，正好以0°的俯仰角拍摄地面中心目标点Pcenter处。相机拍摄的最后一个地面点不再是被动推扫姿态在Tend时刻拍摄的Pend，而是时刻拍摄的的表达式为

4）对日机动姿态规划

当T等于Tend后等比降地速主动推扫成像任务结束，卫星开始姿态机动使帆板对日，恢复长期在轨姿态。

等比降地速主动推扫成像的整个姿态变化过程如图2所示，其中为被动推扫姿态时刻卫星的轨道、为被动推扫姿态时刻卫星的轨道。

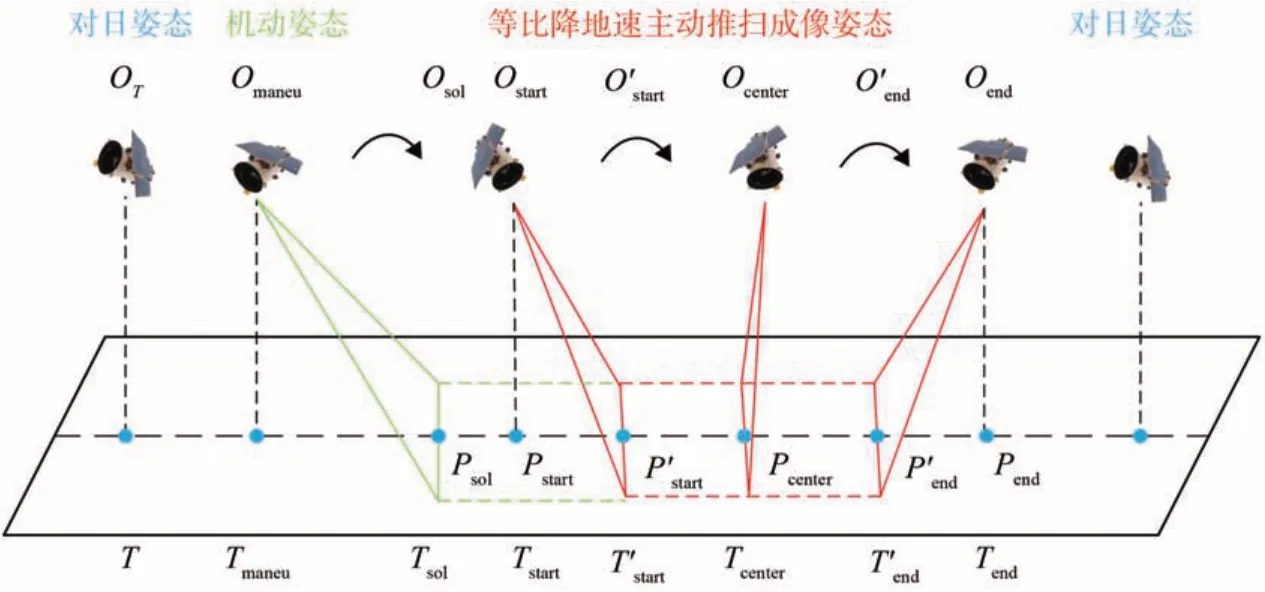
图2 等比降地速主动推扫成像姿态变化过程Fig.2 The attitude variation process of active push-broom imaging with proportional deceleration of ground velocity

2 地面目标点坐标计算

2.1 轨道等比降地速递推

考虑到遥感卫星相机幅宽较大，每次成像任务时间较短，星上中心计算机运行速度较低，为尽可能占用较短的时间进行递推计算，采用二体轨道模型进行递推。短时间内的二体轨道模型递推精度较高，且遥感卫星相机幅宽较大而不会丢失目标点。

设Tmaneu时刻的卫星轨道Omaneu在J2000 坐标系下的位置为rJman=[rJman_x，rJman_y，rJman_z]T，在J2000 坐标系下的速度为vJman=[vJman_x，vJman_y，vJman_z]T，则Tsol时刻对应的轨道Osol在J2000 坐标系下的位置与速度可由Tmaneu时刻使用二体模型递推Tms时间后得到，Tms的值如下：

设Tsol时刻的卫星轨道Osol在J2000 坐标系下的位置为rJsol=[rJsol_x，rJsol_y，rJsol_z]T，在J2000坐标系下的速度为vJsol=[vJsol_x，vJsol_y，vJsol_z]T，位置rJsol与速度vJsol的表达式分别如下：

同理，等比降地速主动推扫过程中各地面目标点对应的卫星轨道Orecur在J2000 坐标系下的位置rJrec与速度vJrec可由Osol为起点，在每个控制周期Tctrl内递推δTctrl时间得到。

2.2 地面目标点坐标计算

在卫星本体坐标系中，相机光轴指向的方向矢量为［20］

式中：α为rop在卫星本体坐标系XbObZb面上的投影与Zb轴方向的夹角；β为rop在卫星本体坐标系YbObZb面上的投影与Zb轴方向的夹角。

在WGS-84 坐标系中，卫星相机光轴指向的方向矢量为

式中：Twi为J2000 惯性坐标系至WGS-84 地固坐标系的转换矩阵；Tio为轨道坐标系至J2000 惯性坐标系的转换矩阵；Tob为卫星本体坐标系至轨道坐标系的转换矩阵。

设等比降地速主动推扫成像的地面目标点Precur在WGS-84坐标系中的位置为rPrec，可表示为

式中：k为正实数，表示对卫星光轴指向方向矢量rWop的缩放倍数；rWrec为rJrec在WGS-84 坐标系下的坐标。

在长半轴ae为6 378.137 km 与短半轴be为6 356.752 3 km 的椭球体地球模型下，地面目标点Precur的地心半径Rrecur由地心纬度λrecur唯一确定。长半轴ae、短半轴be与地心纬度λrecur满足下式：

由式（12）可解得目标点的地心半径Rrecur为

地面目标点Precur的地心距Rrecur与地心纬度λrecur还可由其在WGS-84坐标系下的位置rPrec表示为

由实际的物理含义可知，k为两者中的最小值。通过以上各式即可解算出等比降地速推扫时相机光轴指向地面目标点在WGS-84坐标系下的位置rPrec。

2.3 地面目标点速度计算

为定量评估等比降地速推扫精度，需要对相机光轴在地面移动的速度进行计算。因卫星的控制周期较短，为计算相邻两周期内相机光轴指向地面目标点的移动速度，可将地球考虑为球体［21］。通过计算相邻两个地面目标点的地心角与两点间的平均地心距，即可解算出相机光轴在两地面目标点间移动的距离Lbe与速度Vbe。地心角χ为

式中：λrecur1为第一个点的地心纬度；λrecur2为第二个点的地心纬度；αrecur1为第一个点的地心经度；αrecur2为第二个点的地心经度。地面目标点的地心经度为

相机光轴在两地面目标点间移动的距离Lbe与速度Vbe为

式中：Rrecur1与Rrecur2为两地面目标点的地心距。

3 期望姿态计算

根据卫星实时的轨道OT在WGS-84坐标系中的位置rT与地面目标点Precur的位置rPrec，可解算出卫星指向等比降地速推扫成像目标点的姿态。

卫星轨道坐标系原点Oo为卫星质心Ob，Xo轴指向卫星飞行方向，Yo轴指向轨道角速度反方向，Zo轴指向地心，三轴构成右手直角坐标系。为解算出轨道坐标系下的期望姿态，需确定轨道坐标系在WGS-84坐标系中的投影。

轨道坐标系Xo轴在WGS-84系中的投影ROx为

式中：ωie为地球自转角速度；vT为卫星轨道OT在WGS-84坐标系中的速度。

轨道坐标系Yo轴在WGS-84 坐标系下的单位向量为

轨道坐标系Xo轴在WGS-84坐标系下的单位向量为

轨道坐标系Zo轴在WGS-84坐标系下的单位向量为

在WGS-84 坐标系中，地心Oe、卫星与地面目标点所构成平面的法向量AEul为

法向量AEul在轨道坐标系Xo与Yo轴上的分量AEOx与AEOy分别为

以法向量AEul为欧拉轴，以ς为旋转角，根据欧拉轴角与姿态四元数的转换关系，即可得出轨道坐标系下卫星指向地面目标点Precur的期望姿态四元数qho为

卫星、地心与地面目标点关系如图3所示：

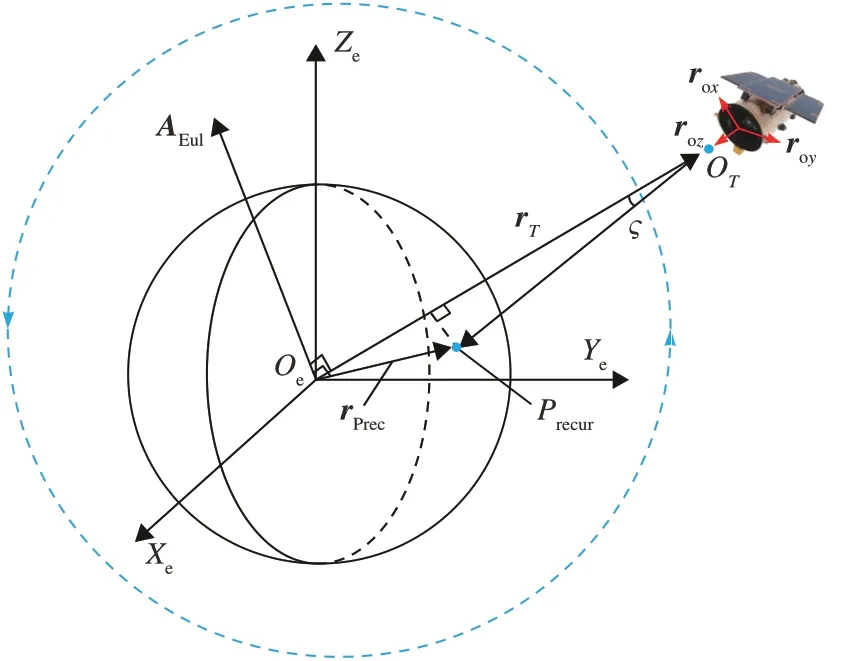
图3 卫星、地心与地面目标点关系Fig.3 Relationship between satellites，the earth’s center，and ground target points

4 数值仿真与卫星在轨验证

4.1 数值仿真

本文进行了两组数值仿真，以验证姿态规划方法在无侧摆与有侧摆情况下不同降速比例的有效性，分别为0°侧摆条件下25%降速比的主动推扫姿态规划仿真，以及15°侧摆条件下50%降速比的主动推扫姿态规划仿真，为进行对比分析，同时进行相同侧摆条件下的被动推扫姿态规划仿真。仿真条件下，被动推扫与等比降地速主动推扫的姿态机动开始时间、机动时间、成像开始时间与成像时长均相同，两种姿态规划方法最直观的区别在于成像期间的地面目标点轨迹因等比降地速而长度不同。

数值仿真以吉林一号高分04A 卫星为仿真对象，仿真条件如表1。

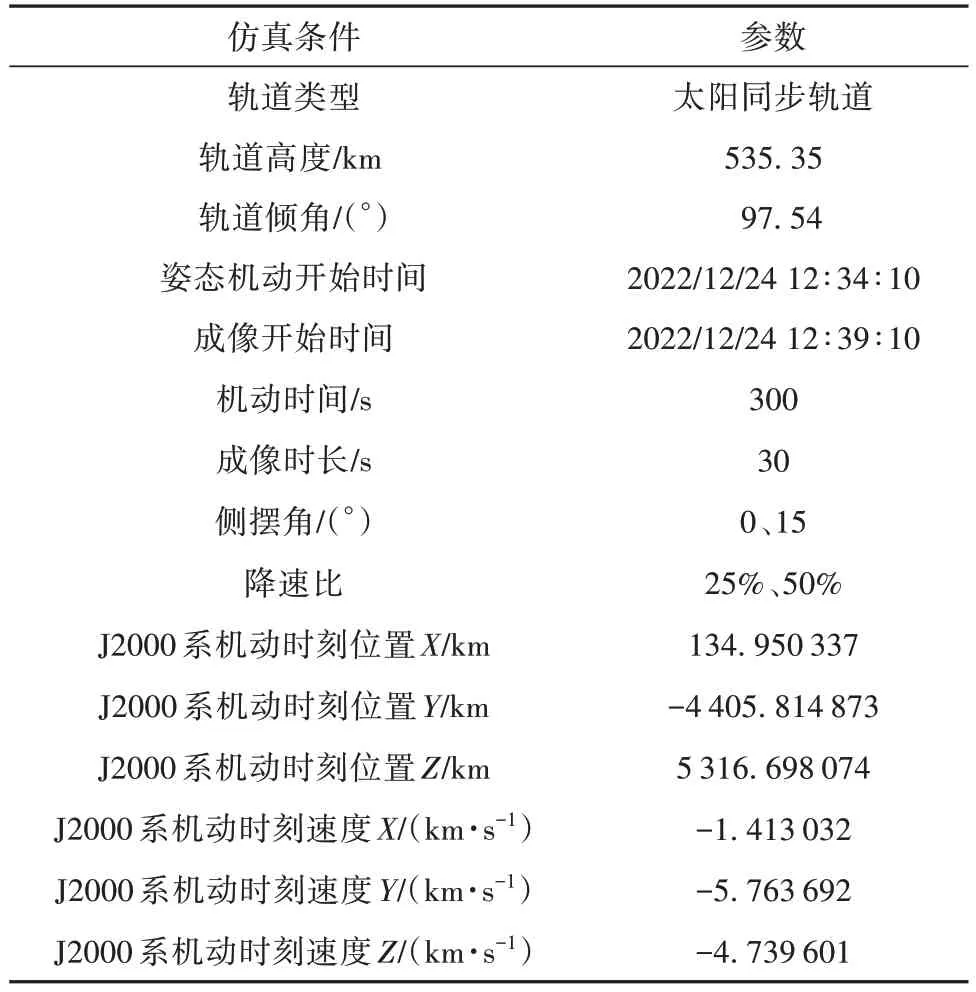
表1 数值仿真条件Table 1 Numerical simulation conditions

两组数值仿真的具体情况如下：

1）卫星0°侧摆、25%降速比仿真

被动推扫规划姿态在UTC 时间725 128 750 s（2022∕12∕24 12∶39∶10）开始成像，成像时长为30 s，相机指向的地面目标点轨迹为卫星星下点在725 128 750～725 128 780 s 内对应的轨迹。在0°侧摆与25%降速比情况下，等比降地速主动推扫姿态相机指向的地面目标点轨迹为被动推扫规划姿态成像中心点725 128 765 s前后3.75 s对应的轨迹，即725 128 761.25～725 128 768.75 s，对应被动推扫成像7.5 s 长度的星下点轨迹。整个任务期间与成像期间地面成像目标点轨迹如图4。

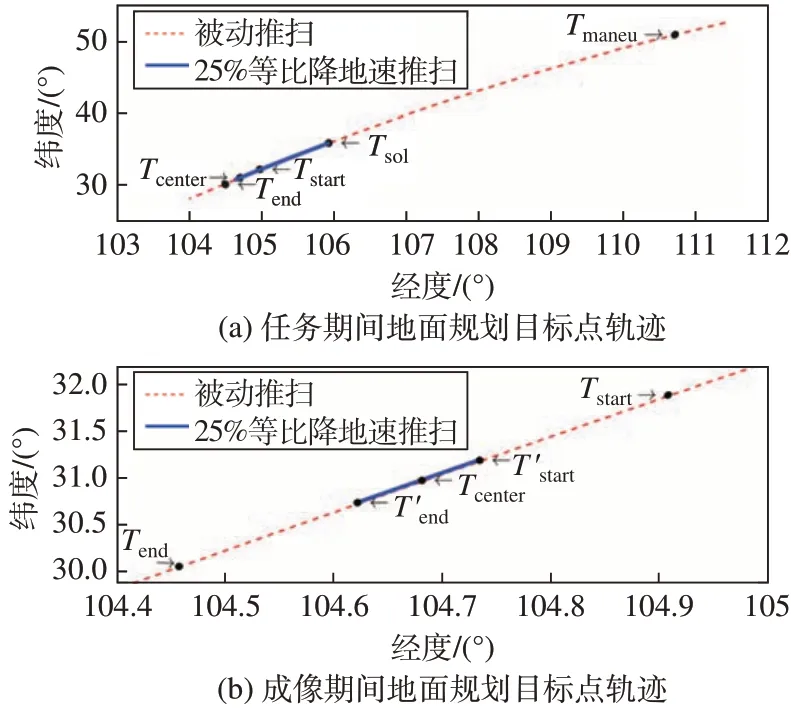
图4 地面规划目标点轨迹Fig.4 Trajectory of the ground target points

等比降地速主动推扫姿态在任务期间的轨道坐标系下姿态角与姿态角速度如图5。

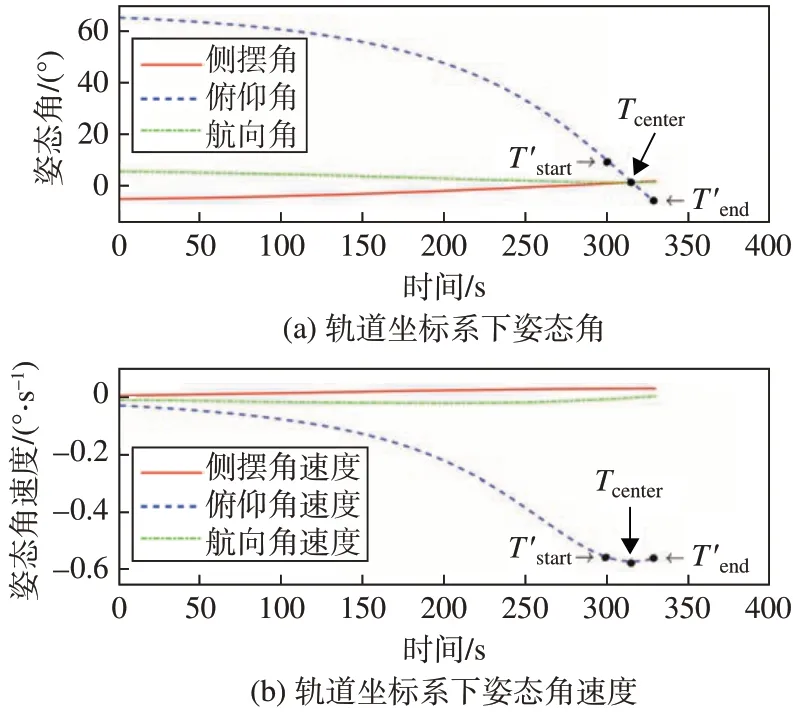
图5 轨道坐标系下姿态角与姿态角速度Fig.5 Attitude angles and angular velocities in the orbital coordinate system

卫星在Tcenter时刻指向成像中心点Pcenter且俯仰角为0°，此时角速度达到最大值-0.569（°）∕s。

成像30 s 期间内，卫星在等比降地速推扫姿态下光轴推扫的距离为53.164 6 km，卫星被动推扫姿态下光轴推扫的距离为212.470 3 km，等比降地速推扫30 s 后的距离误差为0.089%。等比降地速姿态推扫30 s内的平均地速为1.772 2 km∕s，被动推扫姿态的平均地速为7.082 3 km∕s，等比降地速推扫30 s内的速度误差为0.092%。

2）卫星15°侧摆、50%降速比仿真

被动推扫规划姿态在UTC 时间725 128 750 s（2022∕12∕24 12∶39∶10）开始成像，成像时长为30 s，相机指向的地面目标点轨迹为卫星15°侧摆情况下在725 128 750～725 128 780 s 内相机光轴指向的轨迹。在15°侧摆与50%降速比情况下，等比降地速主动推扫姿态相机指向的地面目标点轨迹为被动推扫规划姿态成像中心点725 128 765 s 前后7.5 s对应的轨迹，即725 128 757.5～725 128 772.5 s，对应被动推扫成像15 s长度的成像目标点轨迹。任务期间地面规划目标点轨迹与成像期间地面成像目标点轨迹如图6。

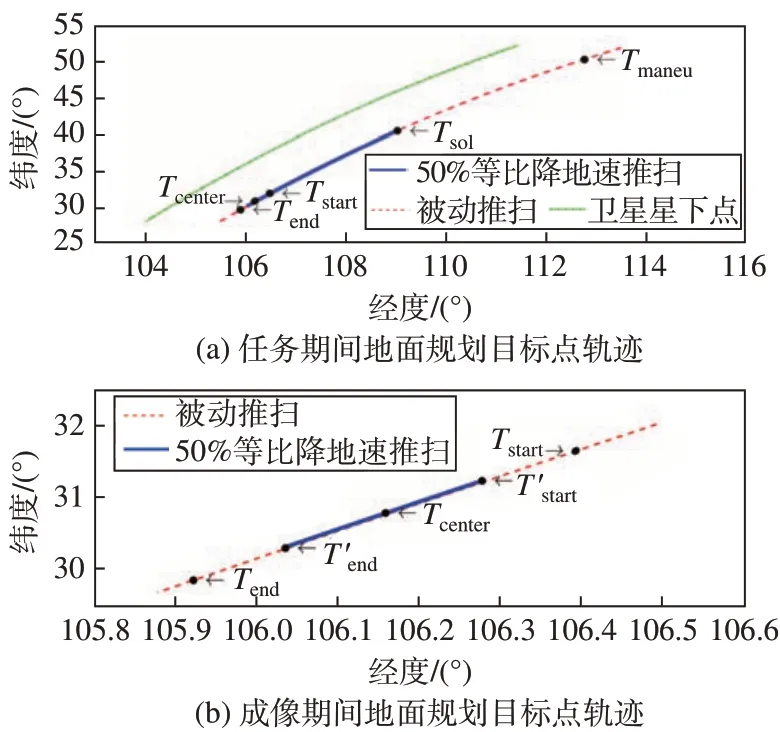
图6 地面规划目标点轨迹Fig.6 Trajectory of the ground target points

等比降地速主动推扫姿态在任务期间的轨道坐标系下姿态角与姿态角速度如图7。

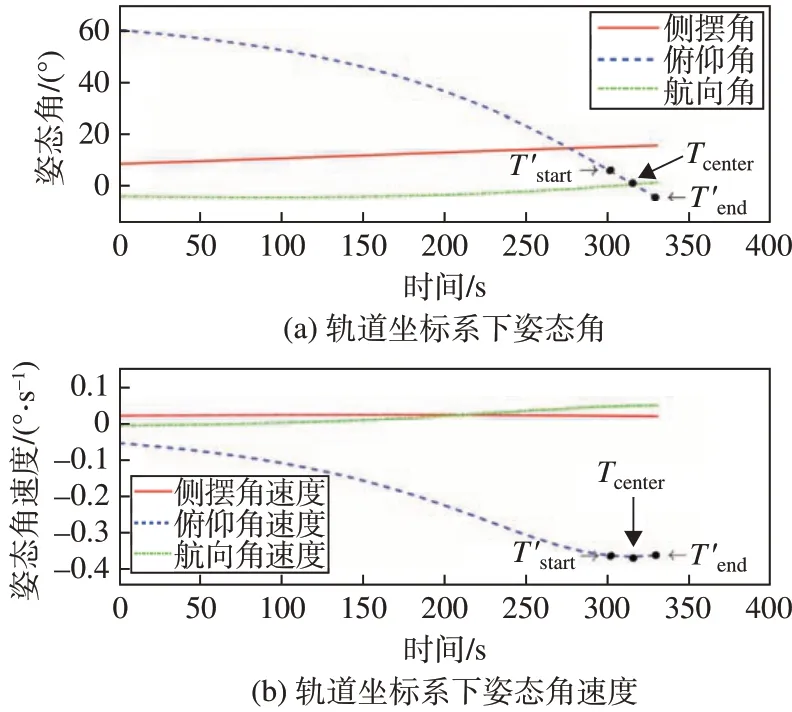
图7 轨道坐标系下姿态角与姿态角速度Fig.7 Attitude angles and angular velocities in the orbital coordinate system

卫星在Tcenter时刻指向成像中心点Pcenter且俯仰角为0°，因降速比50%低于25%，成像期间的最大角速度低于降速比25%的情况，角速度达到的最大值为-0.366（°）∕s。

成像30 s 期间内，卫星在等比降地速推扫姿态下光轴推扫的距离为106.306 7 km，卫星被动推扫姿态下光轴推扫的距离为212.556 5 km，等比降地速推扫30 s 后的距离误差为0.028%。等比降地速姿态推扫30 s内的平均地速为3.543 6 km∕s，被动推扫姿态的平均地速为7.085 2 km∕s，等比降地速推扫30 s内的速度误差为0.028%。

卫星在实现等比降地速主动推扫规划姿态后，随着姿态的变化，相机光轴推扫过的距离也相应地减小，因此会影响到相机成像区域的面积变化。以吉林一号高分04A卫星15 km的幅宽为例，在0°侧摆的情况下对不同纬度地区与不同降速比下卫星相机在60 s内推扫过的面积进行仿真分析，结果如表2。

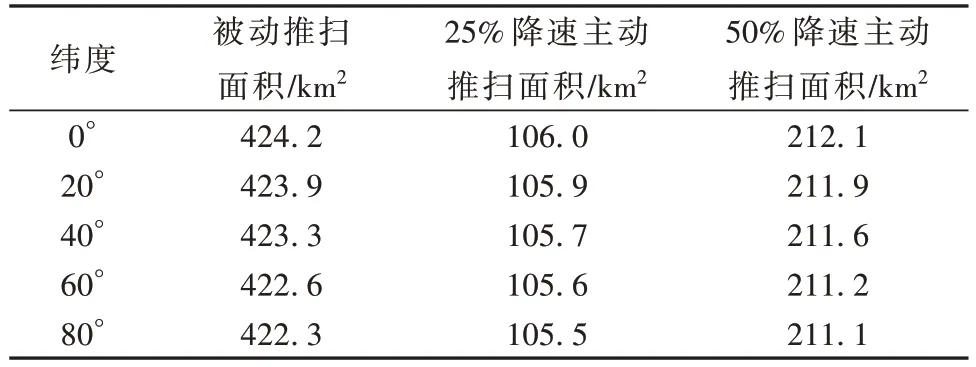
表2 不同条件下卫星的推扫面积对比Table 2 Comparison of push-broom area of satellites in different conditions

以上的仿真结果表明，等比降地速主动推扫姿态规划方法可有效实现相机光轴所拍摄地面目标点的降地速功能，但降地速的同时也会引起星体姿态角速度变大与成像面积变小等问题。在轨使用时需针对卫星实际的姿态机动能力与成像任务的区域面积等情况进行分析。

4.2 卫星在轨试验

本文设计的等比降地速主动推扫姿态规划方法已应用于吉林一号高分04A 卫星的星上软件，为验证算法有效性，进行了在轨试验。卫星在轨试验参数如表3。

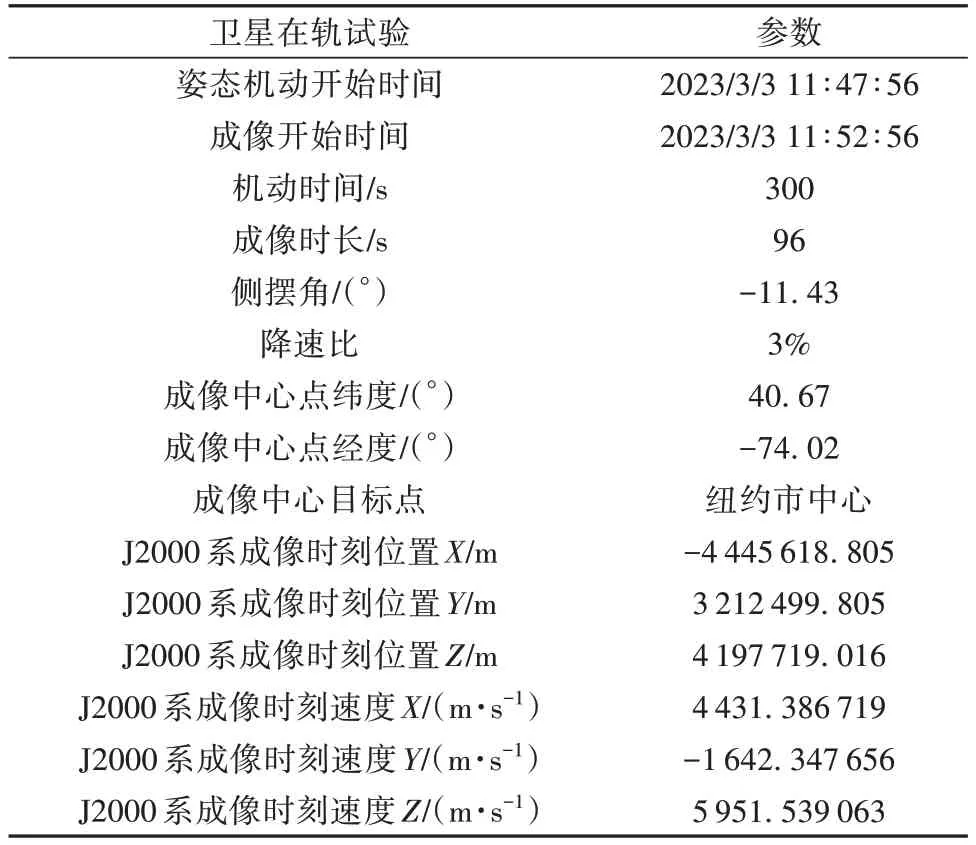
表3 卫星在轨试验参数Table 3 Satellite on-orbit test parameters

卫星在轨试验对境外的纽约市中心进行成像，因此无法完整获取任务期间的实时在轨姿态与轨道数据，只能通过辅助数据获取成像期间存储的姿态与轨道数据。为验证在轨试验的精度，使用卫星在轨的真实轨道数据结合理论期望姿态进行被动推扫仿真作为对比。成像期间等比降地速主动推扫地面目标点轨迹、被动推扫仿真的地面目标点轨迹以及卫星星下点轨迹的对比如图8。

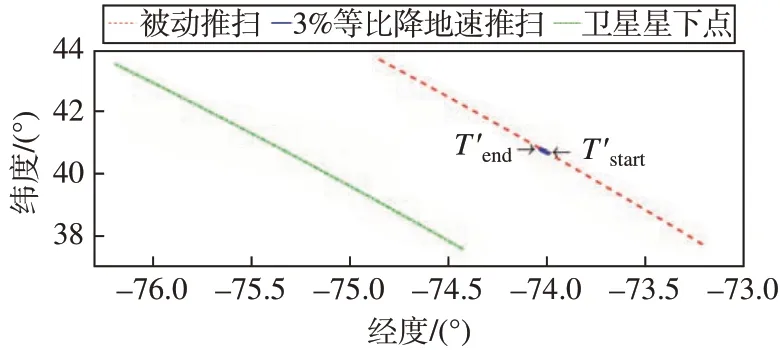
图8 成像期间地面成像目标点轨迹Fig.8 Trajectory of the ground imaging target points during imaging

成像期间规划姿态在轨道坐标系下姿态角与姿态角速度如图9。

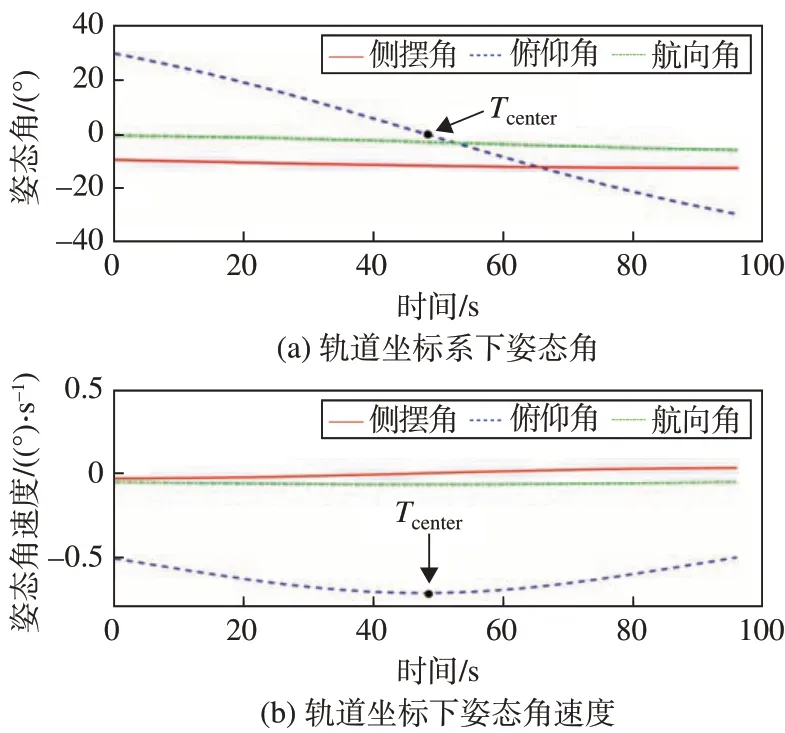
图9 轨道坐标系下姿态角与姿态角速度Fig.9 Attitude angles and angular velocities in the orbital coordinate system

卫星在轨试验的降速比为3%，因此成像期间卫星的俯仰角与俯仰角速度变化较大。俯仰角变化范围为-29.056°～29.537°，俯仰角速度最大值为成像中心时刻Tcenter对应的0.715（°）∕s，明显高于数值仿真中25%降速比与50%降速比的情况。

成像96 s 期间内，卫星在等比降地速推扫姿态下光轴推扫的距离为20.443 km，卫星被动推扫姿态下光轴推扫的距离为675.153 km，等比降地速推扫96 s后的距离误差为0.93%。等比降地速姿态推扫96 s内的平均地速为0.212 6 km∕s，被动推扫姿态的平均地速为7.014 6 km∕s，等比降地速推扫30 s内的速度误差为0.151%。

对纽约市中心进行的3%等比降地速主动推扫的夜间影像以及与阳照区被动推扫的成像结果对比如图10。

图10 在轨试验成像结果Fig.10 Imaging result of on-orbit test

在轨成像结果表明，在通过等比降地速增大积分时间的情况下，光学推扫卫星可以在一定程度上实现地影区的夜光成像。

5 结论

针对光学推扫卫星难以在地影区进行夜间成像的情况，本文提出了一种等比降地速主动推扫姿态规划方法。根据卫星推扫成像的任务参数进行轨道等比降速递推，并计算出轨道等比降速递推后卫星指向地面点的坐标，进而反算出卫星的实时姿态，最后基于吉林一号高分04A 卫星参数对所设计的姿态规划方法进行了数值仿真并进行了卫星的在轨试验。数值仿真中，卫星在0°侧摆角25%降速比的情况下，在30 s 成像期间的等比降地速误差为0.092%，卫星在15°侧摆角50%降速比的情况下，在30 s 成像期间的等比降地速误差为0.028%。吉林一号高分04A 卫星的-11.43°侧摆角3%降速比在轨试验已下传清晰的夜间影像，在96 s 成像期间的等比降地速误差为0.151%。数值仿真与卫星在轨试验结果证明了该方法的可行性与有效性。