碎石土斜坡场地土体水平抗力分布模式研究
2023-12-25陈继彬
彭 麟 ,陈继彬
(1.江苏联合职业技术学院南京分院,江苏 南京210000; 2.成都工业学院,四川 成都610031;3.成都理工大学,四川 成都610059)
0 引言
我国西南地区90%以上输电线塔基础(桩基础) 位于碎石土斜坡场地,桩周土体水平作用力及其水平抗力分布规律是岩土工程界的热点问题。
因斜坡坡度的影响,陡坡场地土体水平抗力的分布规律明显不同于半无限空间假定的水平场地。国外学者通过室内外模型试验、数值模拟等手段对不同坡度条件下砂土、黏性土的土体抗力提出了半经验计算公式[1-4]。我国现行标准[5-7]中以m值法为主估算各类土体的水平抗力,取值范围相对宽泛且建议值仅适用桩的泥面位移量小于3 mm这个位移极限。基于规范[5-7]的不足,研究人员结合大量的工程试验,建议了桩顶不同位移量时m值的(桩侧土体水平抗力系数比例系数)经验取值,并分析了桩身几何特征(桩径、桩长、桩型等)、桩周土性特性(密度、抗剪强度等) 对m值取值的影响,进一步归纳出了m值与上述影响因素的关系表达式[8-16],但研究成果仍主要以为软黏土为主,且对于斜坡场地的研究成果仍较分散。对于斜坡场地条件,一般研究观点认为以水平场地的m值为基准乘以坡度修正系数,对于粘性土而言取为0.3 ~0.6。该折减系数是否适用于碎石土斜坡场地条件下土体抗力分布规律和m值计算仍未有响应的研究和论证。
本文基于西南地区地形地貌特点,以输电线路桩基础为例,结合相似理论,设计并开展了4种坡度(0、15 °、30 °、45 °) 下室内模型桩水平载荷试验,分析不同荷载作用阶段坡度影响下桩侧土体水平抗力随桩深、桩顶位移的分布规律,并提出响应阶段的抗力分布计算方法及计算参数取值建议。研究成果旨在为斜坡场地基础设计提供理论借鉴,具一定的实际工程价值。
1 室内模型试验方案
1.1 斜坡体模型设计
①试验坡度:0 (水平场地)、15 °、30 °、45 °。②试验土体: 取自四川省理县薛城镇某斜坡,土体为稍密碎石土,粒径为3~4 cm,颗粒间充填少许黏性土(见图1a)。土体进行室内筛分后,确定级配比例配置土体:d(颗粒直径) ≥2 mm比例73.6%、d≥5 mm 比 例60%、d≥20 mm 比 例28.8%,配比后见图1b,试验土体的物理力学参数参见表1。

图1 坡体材料图Fig.1 Soil material
1.2 模型桩设计
综合下述2 方面因素确定模型桩相似比为10,其中:
①线塔工程桩基几何尺寸: 桩宽0.8 ~1.2 m,桩长8~10 m,桩身材料C25。
②室内试验台尺寸: 试验在三维地质模拟试验室进行,其长、宽、高分布为1.5 m、1.0 m、1.3 m。
依次设计模型桩见图2,几何参数见表2。试验桩用材料配合比为水泥(42.5 R): 砂: 水=1:1.76: 0.32。桩身密度2.14 g/cm3、弹性模量为27.83 MPa、单轴抗压强度为49 MPa。

表2 桩模型设计参数Table 2 Parameters of pile model

图2 模型桩Fig.1 Model pile
1.3 试验过程
(1) 模型搭建: 首先在试验槽按30 cm 间距标记填筑刻度,分层填筑分层夯实,并在预定深度埋设模型桩。填筑到设计标高后统一削坡,不同坡度试验模型参见图3。

图3 试验模型Fig.3 Test model
(2) 监测点设置: 埋桩的同时埋设监测元件,其中: ①位移百分表分别布设在桩顶及桩身泥面位置(相距约10 cm); ②土压力盒桩前、桩后随桩深共布设8 只,布设深度见图4 示意图(图4 仅为示意图,部分元件因埋设时模型条件所限上下略有移动)。

图4 监测元件埋设示意图Fig.4 Schematic diagram of monitoring element embedding

图5 加载及反力系统Fig.5 Loading and reaction system
(3) 荷载标准: 试验方法为慢速维持加载法,加载方向与坡面方向一致,在桩顶泥面处采用千斤顶按0.3 kN 每级匀速加载,每级加载稳压10 min后每隔2 min 读取百分表一次,待读数稳定后进入下一级荷载试验。当出现桩周土体隆起或桩明显开裂直至破坏的一种情况即可停止加载。
2 土体抗力随深度分布
桩-土体系不同受力-变形阶段土体抗力-深度关系参见图6。
从图6 可见,碎石土斜坡土体抗力在深度方向上呈“凸” 型变化特点,从坡面至桩底大体分为3 段,分别为①桩顶至坡面0.3~0.5 倍桩埋深;
②至桩身挠曲拐点; ③至桩底。其中,第一段抗力随深度变化呈正比变化,第二、三段均呈反比,且抗力在0.3~0.5 倍桩埋深及桩底达到极大值和极小值,在桩身挠曲拐点为0,反映出桩侧土体抗力与桩身形变量直接相关,在桩身挠曲点位置位移为0 (抗力亦为0),下部桩体发生向桩后的变形,桩后土体相应的发挥了一定抗力。
总体上,斜坡场地土体抗力随深度分布表述为下述2 个层面: 一是抗力大小,随斜坡坡度的增大非线性减小,陡坡(45 °) 较缓坡(15 °) 在相同深度处的抗力小15%~30%,这一响应规律受埋深的影响而减弱; 二是抗力最大值深度,随斜坡坡度的增大线性加深,斜坡坡度从15 °增加到45 °,抗力最大值深度从0.3 m 埋深加深到0.4 m。具体试验结果见表3 所示。

表3 不同埋深桩侧土体极限抗力Table 3 Ultimate resistance of soil in different buried depth
3 土体抗力随位移分布
抗力最大值深度至桩底段桩侧土体抗力逐渐减小且受坡度影响程度逐渐减弱,基于此,以桩身上部3 处典型深度试验结果为例分析不同坡度桩侧土压力-位移两者相关关系。
图7 为桩侧土体抗力-位移曲线,即p-y曲线,从曲线可见,桩侧土体抗力在不同深度均随位移均呈双曲线变化态势,先线性增大后逐渐趋于稳定而后达到极限抗力状态。不同深度具体表现如下:
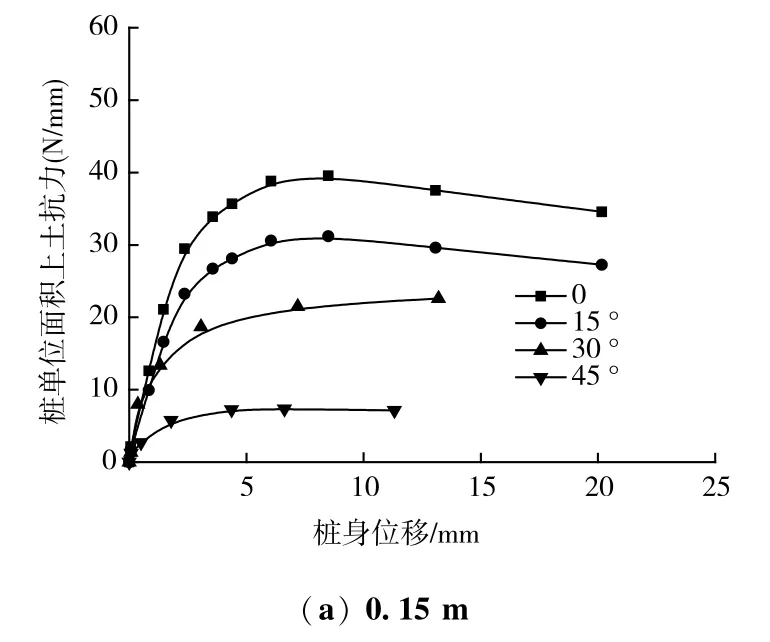
图7 不同坡度桩侧土压力-位移曲线Fig.7 Earth pressure displacement curve of pile side with different slope
因斜坡坡度改变了桩基受力的半无限空间状态,浅层土体桩前提供抗力的范围减弱使其在较小荷载作用下即刻抗力极限状态; 但随着深度的逐渐加深,桩前土体抵抗水平作用力的能力逐渐摆脱坡度的影响,同时受桩顶~泥面范围内作用的水平推力向下传递深度的限制,在相同荷载等级条件时深层土体并不会与浅层土体同步进入极限抗力状态,如图7c,该深度范围内p-y曲线始终为线性状态,但随桩顶作用荷载的增大会有进入极限状态的可能,说明土体抗力随深度增加其发挥的能力具有渐进性。
4 抗力分布模式及计算方法
4.1 分布模式
综合归纳斜坡场地桩侧土体水平抗力随深度、随荷载、随位移的变化规律,按桩侧土体是否进入极限状态将其分布模式为3 个阶段,如图8所示。
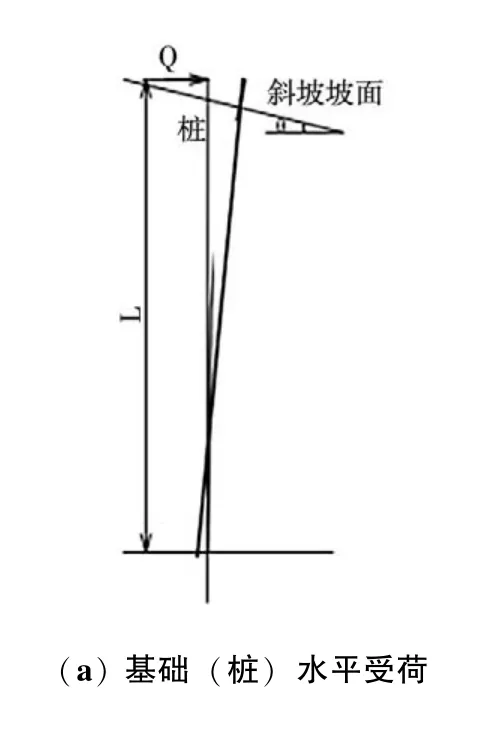
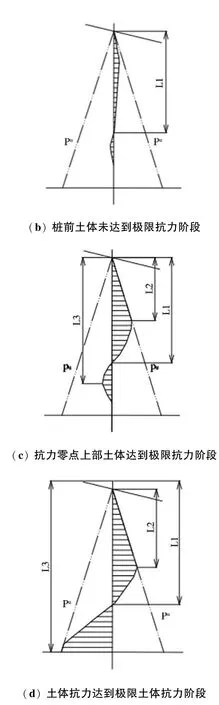
图8 斜坡场地桩侧土体抗力的分布模式Fig.8 Distribution model of soil resistance along pile side of slope length
(1) 图8 (b),桩顶~泥面范围内水平作用力Q小于土体临界荷载Pa时(即Q<Pa),桩侧土体水平抗力p线性增大,且桩埋深范围内均在土体极限抗力Pu包络线范围内;
(2) 图8 (c),当Pa≤Q<Pu,仅坡面至0.3~0.5 倍桩埋深(抗力最大值深度) 范围内,桩侧土体抗力达到或接近极限抗力状态,并随作用荷载的增大,极限状态深度范围逐渐加深;
(3) 图8 (d),Q≥Pu,桩埋深范围土体抗力均达到极限抗力状态。
4.2 计算方法
依据桩侧土体抗力分布模式,做如下假设:1)L表示桩长、d表示桩径(宽),桩底铰接而桩顶自由,水平荷载Q作用在桩身泥面位置,位移为y0; 2) 深度方向上,土体水平抗力系数kx、极限土反力pu均线性增大; 3)p-y曲线为双曲线变化,当土体进入极限抗力pu后,p不随y的增大而明显增大; 4) 水平荷载作用下桩仅发生绕某点的

L1、L2计算可参照(2) 中假设。当z=L3时,pu=-pu,可进一步计算出L3。
4.3 参数确定
上述各式的求解关键是准确计算土体极限抗力pu以及土体抗力系数kx。确定方法如下:
(1)puθ的确定
从表3 可见,每一坡度下的puθ(θ=15°/30°/45 °) 与水平场地下pu0比值分2 段:
①坡坡面至0.3~0.5 倍桩埋深L2,两者比值与斜坡坡度直接相关,坡度15 °,30 ° 和45 °时,其比值分别为0.75,0.61 和0.49。可近似表述为式8。
②0.3~0.5 倍桩埋深至桩底(即L3≤z≤L2),比值则为常数1,即斜坡坡度的影响可忽略不计。这说明斜坡坡度对桩侧土体水平抗力的影响具有深度效应,到达一定深度后桩土土体能够提供抗力的范围即恢复到水平半无限空间场地桩土,可按水平场地的工况计算土体极限抗力。
(2) 土体抗力系数kx
根据4.1 节假定2),土体抗力系数kx可表述为kx=mz。规范[5]认为m值取值与实际荷载、允许位移相适应,如果根据试验结果求桩的m值,得到m值随泥面位移(y0) 变化的关系曲线,如图9 所示。按试桩的地基土进行分类,确定其m值的取值范围应为100 ~300 kN/m4(泥面位移y0为1.5~3 mm),但是从图8 可见,因为斜坡坡度的存在,泥面处桩身发生3 mm 位移时计算得到的m值明显小于规范建议值明显要小。故而,根据图8 中m值随y0变化表现出的幂函数衰减关系。进一步拟合得到其表达式为:
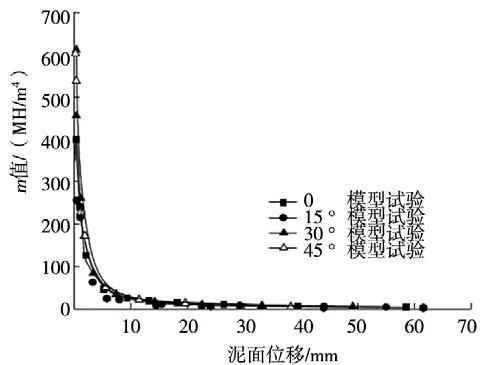
图9 m 值随y0变化曲线Fig.9 Curve between m value and mud surface displacement
式中y0/b为土体应变,b为桩宽(或直径),Cm为土体发生单位应变时相应的m取值,根据试验或经验确定。其中:
①k表示m值随y0增大而减小的幅度,本次试验所用碎石土k为-0.8~-1;
②系数Cm与m值量纲相同。基于土体抗力定义,对比斜坡场地下同一深度Cm|斜坡与水平场地条件Cm|水平之间关系,得到公式6。

5 结论
本文通过桩基静载荷试验研究碎石土斜坡土体水平抗力随深度、随荷载、随位移的变化特点,进而归结出土体抗力的分布模式及计算公式。主要结论如下:
(1) 坡土体抗力随深度变化可分为线性增大段、波动增大-减小段、反向减小段,呈上下小中间大的凸型; 而随位移变形呈双曲线变化; 土体抗力随深度上的发挥能力具渐次性;
(2) 土体抗力随深度、位移综合分布形式可以分为桩前土体未达到极限抗力阶段、抗力零点上部土体达到极限抗力阶段、土体抗力达到极限土体抗力阶段; 不同阶段主要计算参数均为土体极限抗力和土体抗力系数;
(3) 斜坡场地与水平场地下两者土体抗力极值比值在抗力最大值深度以上近似1/1+tanθ关系,以下近似为1,这也充分说明斜坡坡度对桩侧土体抵抗桩身变形能力具有弱化效应;
(4) 斜坡碎石土场地水平受荷桩的m值随泥面位移变化呈现幂函数衰减关系,基于此对规范计算m值公式进行修正来确定kx。
