基于决策树的实民用建筑供电可靠性智能评估算法

宋立立，孙 妍

（北京市建筑设计研究院有限公司，北京100045）

0 引言

民用建筑内的供电系统包含一个十分庞大且复杂的电力网络，其与发电厂的发电、变电所的变电、电力设施的输电、以及用电器的电力使用环环相扣，任何一个环节出现故障，均会导致供电错误。而为了保证高压电下的人身安全，一旦出现电力故障，电力设施就会自动停电。但是很多配电网络中缺少相应的备用电源，一旦发生故障，整栋民用建筑均会停止供应电力，供电可靠性极差。因此，在一栋民用建筑中，供电可靠性评估是十分重要。文献［1］ 结合工业用户对电力设备运行的影响，在现有的电压暂降供电可靠性评估算法中，完善了工业过程中电力运行对其安全性能的影响，设计了一种新的供电可靠性评估方法，基于经济等效时间，建立了一个可靠性的定量评估指标，在过程免疫节点中，将模糊物元的基本结构以及安全损失等权重作为电压的供电安全指标。文献［2］ 将改进梯度提升决策树－蒙特卡罗法应用于可靠性分析中，在数据库中建立决策树的近似模型，并以此生成样本点作为失效面的有效元分析数据集，通过近似结构完成超大型集装箱船的可靠性分析。由试验可知该方法的误差在允许范围之内，且计算时间大幅度减少，将该方法应用于供电可靠性评估中后，可以显著提高评估精度与评估效率。

本文综合以往研究方法的优势，设计了一种基于决策树的民用建筑供电可靠性智能评估方法，用于提高供电可靠性的评估准确率。

1 基于决策树设计民用建筑供电可靠性智能评估算法

1.1 提取民用建筑供电故障节点信息熵

在评估民用建筑供电设备的可靠性时，首先需要提取其故障节点的信息熵，将不同故障部件用于整机试验的组合，计算其测试次数与失败次数，并分别计算系统的可靠度。此时，民用建筑故障的供电节点中，信息源输出的信息熵可以表示为：

式中：Sh表示民用建筑故障节点中信息源输出的平均信息熵；Li表示某故障的信息源节点输出信息的次数；L0表示第一次出现信息的节点数［3］。在该供电系统共中，可以将若干个信息源看作同一个实验数据集，此时系统内的总信息熵可以表示为：

式中：Sz表示供电可靠性系统内的总信息熵；Pk表示子系统第一次试验的成功次数；Pm表示子系统内第一次试验的失败次数［4－5］。基于总信息熵，可以分别得到成功熵和失败熵：

式中：Scg表示试验中成功的信息熵；Ssb表示失败信息熵；Lni和Lfi则分别表示信息在成功与失败中得到的部件故障总量。得到系统内成功评估与失败评估的可靠度，并提取民用建筑供电故障节点信息熵。

1.2 基于决策树修正可靠性评估数据

通过决策树算法可以更好地训练民用建筑供电可靠性算法，修正并筛选更具代表性的数据。假设训练样本中共有x个训练样本，则可以得到标签在回归函数中的连续值：

式中：Th(x) 表示函数空间中h个假定参数的最优解；gn(x) 表示梯度下降方向的迭代值。在学习器中可以分别获取加权参数，通过先后顺序的排序产生相应的预测值，如图1 所示。

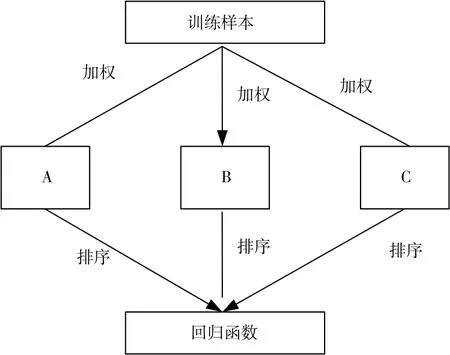
图1 训练样本梯度排序与预测Fig.1 Schematic diagram of personnel dangerous behavior monitoring

如图1 所示，对学习器进行加权预测的过程，即为对决策树训练样本进行数据修正的过程，此时可以产生若干个学习性能不同的学习器，其计算公式为：

式中：k(x) 表示某学习器的加权预测结果；fd表示第d 个学习器在不通过加权指标下减少样本权重的预测参数；pd(x) 表示样本在均方根误差中的方差均值函数［9］。在得到了不同学习器的预测结果后，依据排序的方法，得到供电可靠性数据在修正后的线性回归函数。在整个数据的运行过程中，为减小外部环境对实验周期中民用建筑供电可靠性智能评估算法的影响，可以采取不断修复的方式，减少维修所需要的时间。此时可以适当引入随机变量：

式中：δf表示随机变量的最终函数值；f表示机组在故障数据重组期间的独立变量，当f≤0 时，意为数据重组失效，当f＞0 时，表示数据重组成功［10］。在故障间隔期间可以以此排序统计量不同时段的数据组可以表示为：

式中：(t1，δf1) 表示某故障间隔时间内的数据顺序统计量，该节点内的故障统计量总数为n；t1表示故障间隔时间；δf1表示该事件内的数据组随机变量结果［11－13］。结合以上公式，可以修正并补充为不完整的民用建筑供电可靠性数据。

1.3 建立民用建筑供电可靠性评估模型

在得到了较为完整的供电可靠性数据后，可以通过评估模型确定可靠性评估结果，其在民用建筑内的算法流程如图2 所示。

图2 算法流程Fig.2 Algorithm flow

如图2 所示，需要在评估建立供电可靠性前，首先编写矩阵向量，此时的分层支路矩阵共分为6个节点，其在对角线上的元素分别为：

式中：Hij表示支路上各元件的存在形式，其分别需要依据不同的源节点与支路节点一一排序［14－15］。通过该向量可以获取可靠性指标在算法末端的连接值，通过搜索末端点母线的关联状态，可以得到可靠性的影响结果：

式中：fk表示民用建筑供电可靠性智能评估结果；fi＋1表示在上一个节点的关联结果。通过该模型，可以得到民用建筑供电可靠性评估结果。

2 试验研究

2.1 民用建筑线路连接分析与数据预处理

为了测试基于决策树的民用建筑供电可靠性评估方法的有效性与准确性，设计如下试验。

将某市的一栋民用建筑作为试验的主要场地，其电路连接结构如图3 所示。

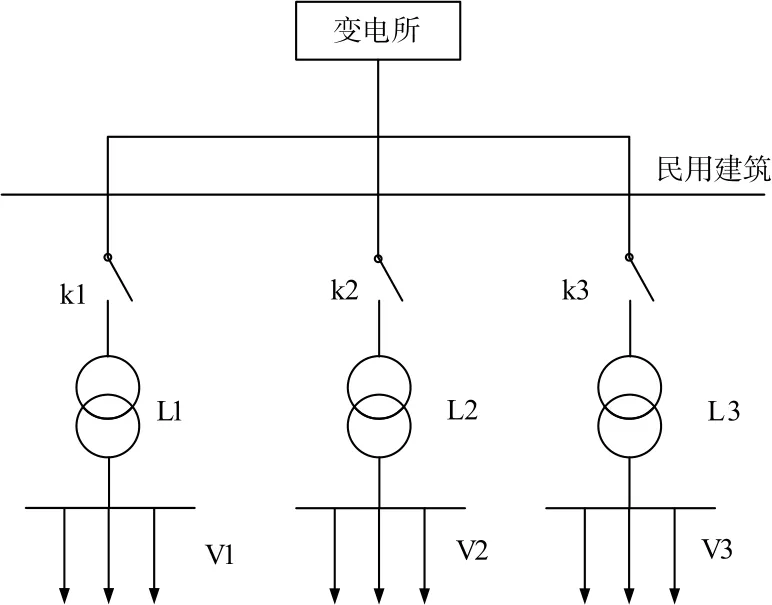
图3 电路连接示意图Fig.3 Schematic diagram of the circuit connection

如图3 所示，该建筑中只有一路独立电源，与变电所相连接，在电网中的电力传输到民用建筑中后，通过三个开关k1、k2、k3分别运输到电力设备中。图3 中的L1－L3分别表示电力使用设备，在该民用建筑的线路中属于主要耗电设备。三个耗电设备的主要电力负荷可以用V1、V2、V3表示与计算［16］。通过电能检查装置获取民用建筑供电可靠性的初始数据，将其作为真实的数据样本，导入到仿真分析软件MATLAB 中，并在该环境下完成主成份指标的信息输入，首先需要进行数据的归一化处理。由于不同数据之间量纲不同，导致网络训练时的收敛能力也存在差异，因此在获取最佳的收敛性能时，需要将每一个数值均计算成为同等程度，即对其进行归一化处理。归一化处理可以在MATLAB 软件中进行，其计算公式为：

式中：ky表示归一化过程中分量数值在函数中的结果；kmax和kmin分别表示y轴坐标中数据的最大值与最小值；h表示初始的电力数据；hmax和hmin分别表示x轴坐标中数据的最大值与最小值。将每一个在x轴与y轴中的分量均调整在（－1，1） 之间，以保证其网络训练的特性。除此以外，将randperm （） 函数作为随机排序的工具，在训练周期过长或者难以完全收敛的情况下，使用该工具，避免数据集中的现象。

2.2 算法参数设置

将算法训练集中的网络节点分为三个部分，最佳节点数量计算公式为：

式中：xn表示民用建筑供电可靠性智能评估算法中不同节点数量的最小均方差；xi表示输出层的节点数量；mp隐藏的节点数量；da表示平方变化常数。使用该公式，可以得到不同节点数量下的网络性能，如图4 所示。

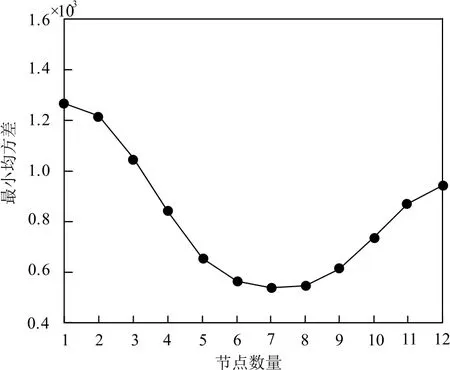
图4 节点数量与网络性能之间的关系Fig.4 Relationship between the number of nodes and the network performance

如图4 所示，随着节点数量的变化，最小均方差由1.28×10－3下降至0.54×10－3，降至最底端之后又回升至0.92×10－3，其在节点数量1－12 时是一个“U” 型的标志，可见当节点数量为7 时，网络性能最佳，因此在试验中选择节点数量为7。

2.3 算法仿真测试

在试验中，分别设定测试集的网络参数，最大迭代次数为500，训练精度为0.001，学习率为0.25，动量因子为0.55。为保证仿真结果的准确性与有效性，将民用建筑电路连接示意图中的三个供电分量作为不同的变量，分别对其误差与平均适应度进行测试。将本文的评估算法分别与传统的“经济等效时间算法”、“改进梯度提升决策树－蒙特卡罗法” 相对比，依据图5 判断三种不同评估算法的精度。

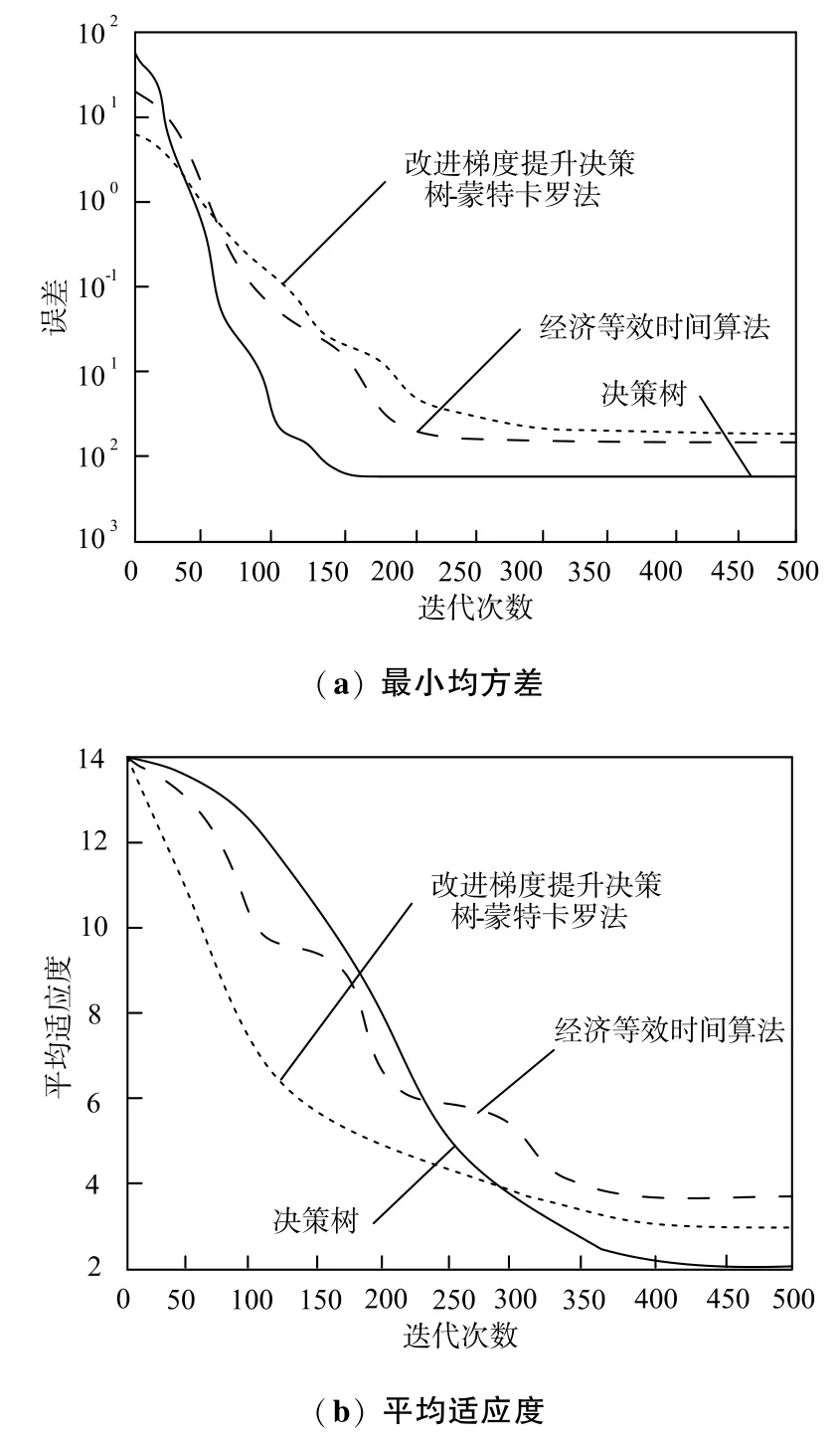
图5 供电可靠性评估结果Fig.5 Assessment results of power supply reliability

如图5 所示，在最小均方差的测试中，本文算法在三种算法中收敛速度最快，经济等效时间算法在最小均方差的测试中达到最小值的迭代次数为234，在三种算法的收敛速度中为第二，改进梯度提升决策树－蒙特卡罗法迭代结束的时间最慢，在第345 次才达到最小均方差。且三种算法的收敛精度也有一定的差别。在巡游过程中，使用适应度的最大值与平均值作为平均适应度的表现过程，通过500 次的迭代运算可以明显看出，随着不断的迭代，三种算法的平均适应度均呈现出下降趋势，且到了最大迭代次数时，均满足了适应度的要求值。其中本文设计的决策树算法平均适应度最小，在向着最优解变化的过程中，能够满足可靠性评价的精度需求。

3 结语

本文依据决策树，设计了一种民用建筑供电可靠性智能评估算法，综合判断某民用建筑的供电能力，并快速获取评价的函数值，可以在去关联的条件下，划分电网结构的拓扑指标，减少不必要的、不完整的数据节点，保证评估算法的准确性，且能够满足可靠性评价的精度需求。