带斜撑巨型框架－核心筒结构协同分析的哈密顿对偶体系∗

胡启平 ，林 凯 ，周 娟

（1.河北工程大学 土木工程学院 河北 邯郸； 2.邯郸职业技术学院 河北 邯郸）

0 引言

结构大师Fazlur Khan［1］于1972 年首次提出带斜撑巨型框架，工程师们常在设计巨型框架时增加巨型斜撑来提高结构的抗侧刚度以及结构整体稳定性［2］。带斜撑巨型框架－核心筒结构抗侧刚度较大，整体稳定性较好，在超高层建筑结构中应用较多。国内有工程实例采用带斜撑巨型框架－核心筒结构体系，例如天津高银117 大厦，深圳平安金融中心等。支撑方式不同会对巨型框架－核心筒的破坏机理和抗震性能产生影响［3］。邹勇强等［4］对钢框架－混凝土核心筒结构进行分析，在钢框架设置巨型斜撑，可以显著地提高结构的刚度、钢框架与核心筒的协同工作性能。陈麟等［5］对设置巨型支撑的巨型型钢混凝土框撑－核心筒结构进行分析，设置巨型支撑可增大外部巨型框架的抗侧刚度，使结构的整体抗侧能力得到显著提高，在地震作用下，外部巨型框架可作为第二道抗震防线，提高整体结构的抗震性能。包世华等［6］在连续化的基础上，计算出框筒、筒中筒在水平荷载作用下结构的侧移与内力。郭伟亮等［7］以结构连续化方法为基础，对斜交网格筒结构进行了简化分析，推导了结构在三种水平荷载作用下的侧移公式。李剑等［9－10］在连续化的基础上，建立了带斜撑巨型框架－核心筒的简化模型，建立问题的平衡微分方程，求解出带斜撑巨型框架－核心筒结构在水平荷载作用下的侧移和内力。胡启平等［11－15］将建筑结构的各抗侧力单元看作具有弯曲变形、剪切变形的铁摩辛柯梁，提出了建筑结构分析的并联铁摩辛柯梁模型，用哈密顿力学的方法对框架－剪力墙、筒中筒结构进行分析，采用精细积分法求解了结构的内力与变形，具有推导过程简单，精度较高等优点。

本文沿用李剑等［10］提出的连续化模型，将带斜撑巨型框架与核心筒分别等效为悬臂梁，等效后的悬臂梁具有弯曲刚度和剪切刚度。采用并联铁摩辛柯梁模型，在哈密顿力学体系下导出结构协同分析的哈密顿正则方程，用精细积分法计算结构在水平荷载作用下的内力及变形，避免了繁琐的数学和力学推导，数值计算精度较高。本文方法可准确分析带斜撑巨型框架与核心筒协同工作性能，在初步设计阶段可对结构方案进行试算和快速分析。

1 计算模型

带斜撑巨型框架－核心筒结构是一种双重抗侧力结构体系，抗侧力单元由外部巨型框架与内部核心筒构成。在水平荷载作用下，外部巨型框架与内部核心筒通过楼板的作用协同工作，共同抵抗水平方向产生的倾覆力矩和剪力。对带斜撑巨型框架－核心筒结构协同分析时，将带斜撑巨型框架与核心筒分别等效为底端固定、上端自由的悬臂梁，将楼板等效成刚性连杆，建立带斜撑巨型框架－核心筒协同分析的计算模型［10］，如图1 所示。建立模型时采用如下基本假设： （1） 结构处于弹性工作阶段。（2） 外部巨型框架与核心筒之间通过每层的刚性楼板进行连接。（3） 楼板在自身平面内刚度无穷大，变形可忽略。带斜撑巨型框架与核心筒之间通过楼板相互联系并协同工作。

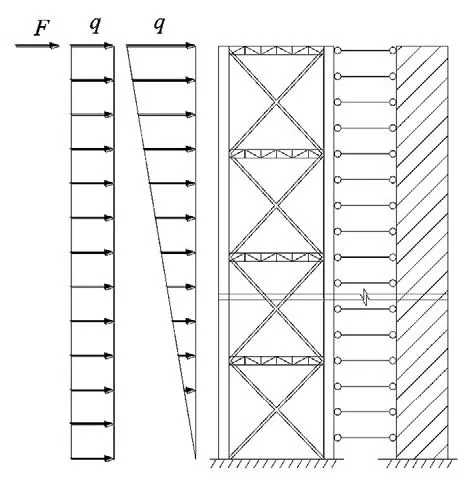
图1 带斜撑巨型框架－核心筒计算简图Fig.1 Calculation diagram of mega－braced frame－core tube

假定建筑结构的各个抗侧力单元都具有弯曲变形、剪切变形，均可看作竖放的Timoshenke 梁。楼板在自身平面内是刚性的，将楼板的作用沿高度连续化，采用并联铁摩辛柯梁模型［13－14］对带斜撑巨型框架－核心筒进行协同分析。带斜撑巨型框架－核心筒结构有巨型框架与核心筒两个抗侧力单元，带斜撑巨型框架的等效抗弯刚度为E1I1，等效抗剪刚度G1A1，侧移为ν1，截面转角为θ1。核心筒等效抗弯刚度为E2I2，等效抗剪刚度为G2A2，侧移为ν2，截面转角为θ2。由基本假设可知，带斜撑巨型框架与核心筒侧移相同，即ν＝ν1＝ν2，作用在结构上的总的水平分布荷载为q。

带斜撑巨型框架－核心筒结构中的带斜撑巨型框架是由巨型柱，斜撑以及环带桁架组成。四根巨柱与斜撑在两个方向相连，形成一个空间桁架筒。在对带斜撑巨型框架简化分析时，假设材料是线弹性的，带斜撑巨型框架均为等截面。假设结构承受对称水平荷载，且不考虑结构的扭转效应，选择一榀带斜撑巨型框架进行分析，计算简图如图2 所示。带斜撑巨型框架的总高度、总宽度分别为H、B，巨型柱的区段高度为h，巨型柱的抗弯刚度EcIc，巨型柱的轴向刚度EcAc； 斜撑的抗弯刚度EbIb； 斜撑的轴向刚度EbAb； 环带桁架的等效抗弯刚度EtIt； 环带桁架的等效轴向刚度分别为EtAt。巨型柱、斜撑的抗弯刚度可依据材料力学公式直接求解，环带桁架等效抗弯刚度以及轴向刚度的计算参阅文献［9］。

图2 带斜撑巨型框架平面模型Fig.2 Plane model of mega－frame

取巨型柱高度为h 的区段推导带斜撑巨型框架的抗弯刚度、抗剪刚度，计算简图如图3。将带斜撑巨型框架等效为具有抗弯刚度和抗剪刚度的悬臂梁，等效后的抗弯刚度E1I1、抗剪刚度G1A1用矩阵位移法进行求解，计算方法可以参阅文献［9］。计算公式如下：

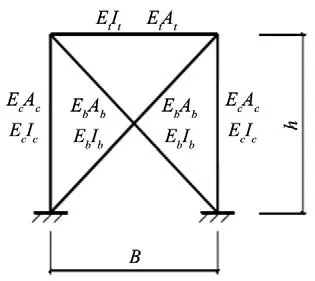
图3 巨型柱区段高度为h 的计算简图Fig.3 Calculation diagram of the height of with diagonal braces giant column section h

其中α＝arctan(h／B)

带斜撑巨型框架－核心筒结构中的核心筒为带连梁的核心筒，连梁连接四片“L” 型剪力墙构成核心筒。带连梁核心筒可采用双肢墙的力学模型进行分析，引入等效刚度的概念，推导出带连梁核心筒结构等效抗弯刚度E2I2、等效抗剪刚度G2A2，具体计算方法可参考文献［9］。

2 带斜撑巨型框架－核心筒协同分析的哈密顿体系

带斜撑巨型框架－核心筒结构具有两个抗侧力单元，将每个抗侧力单元看作为竖放的铁摩辛柯梁，均考虑其弯曲变形和剪切变形，形变势能为

楼板是刚性的，故不用考虑其形变势能。外力势能为

则带斜撑巨型框架－核心筒结构的总势能为

拉格朗日函数为结构的总势能密度，也就是结构的单位高度的总势能。根据带斜撑巨型框架－核心筒结构的总势能表达式，可得到结构的拉格朗日函数为

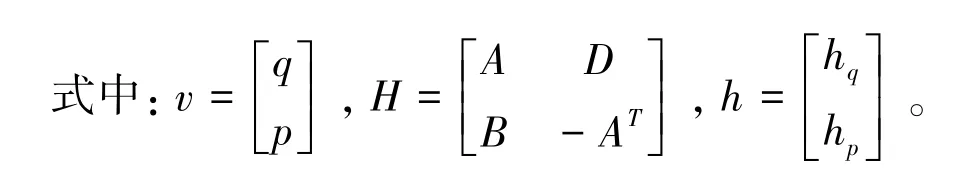
3 数值计算

公式（10） 为带斜撑巨型框架－核心筒结构协同分析的哈密顿正则方程，该方程是对偶的一阶微分方程组。哈密顿体系建立起来后进行求解时需要给出边界条件。对于我们所研究的高层结构，底部固定，可取qa＝0； 顶部自由，可取pb＝0。qa为结构底部广义位移；pb分别为结构顶部广义力。采用两端边值问题的精细积分法［8］，可以求解结构各结点的广义位移、广义力，即[q，p]T＝[v，θ1，θ2，V，M1，M2]T，V为结构的总剪力，M1，M2分别为带斜撑巨型框架、核心筒的弯矩，整个求解过程可通过简单编程来实现。求得外部巨型框架的弯矩为M1(x) ，巨型柱的轴力可用应力乘以截面面积进行求解［9］：

巨型框架的水平剪力是由巨型柱的剪力和斜撑轴力的水平分量承担。巨型框架的剪力为V1(x) ，巨型柱的抗剪刚度GcAc，巨型斜撑的抗剪刚度为GbAb，

则巨型柱剪力［9］：

4 计算实例与分析

选取参考文献［10］ 的算例进行分析，带斜撑巨型框架－核心筒结构模型如图4 所示。结构总高度为600 m，结构总宽度为60 m，巨型柱区段高度为60 m，结构层高为5 m，核心筒宽度为30 m，核心筒厚度为1.2 m，墙肢长度为12.5 m，连梁高度为1 m，巨型柱截面尺寸为5 m× 5 m，巨型斜撑尺寸为1800 mm×900 mm×50 mm×150 mm，环带桁架杆的尺寸为1000 mm×800 mm×100 mm×100 mm，钢材的弹性模量2.06× 105MPa，混凝土的弹性模量为3.6× 104MPa。采用文献［9］ 计算方法，求得带斜撑巨型框架的等效抗弯刚度E1I1＝3.4× 1015N·m2，等效抗剪刚度G1A1＝1.75×1011N； 核心筒等效抗弯刚度E2I2＝5.56× 1014N·m2，等效抗剪刚度为G2A2＝7.48× 1011N。结构承受顶点集中荷载为60000 kN。

图4 带斜撑巨型框%架－核心筒体系Fig.4 The system of mega－braced frame－core tube building

对上述算例我们采用本文提出的方法进行了计算。为便于比较，我们还采用空间模型（如图4所示） 用有限元方法进行了计算。

4.1 结构侧向位移

采用本文方法求得的带斜撑巨型框架－核心筒顶点侧移为1233.90 mm，文献得到的顶点侧移为1234.74 mm，采用有限元求得的顶点侧移为1226.4 mm。本文求得的顶点侧移和文献以及有限元结果误差均不超过1%。本文得到的结构侧向位移与有限元结果基本吻合，如图5 所示。结构的侧向变形呈“弯曲型”。底部楼层的层间侧移较小于顶部楼层的层间侧移，层间侧移角随着楼层高度的增加依次增大。

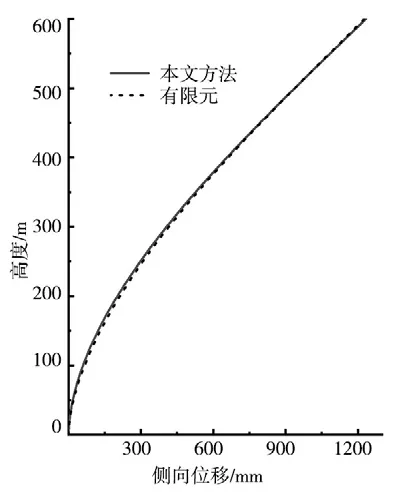
图5 结构侧向位移Fig.5 Lateral displacement of structure

4.2 结构的内力分配

以巨型柱的区段高度60 m 为控制点，求得的内力值如表1

图6 为结构的弯矩分配图。由图可知，采用哈密顿力学方法求得的弯矩与有限元得到的结果基本吻合带斜撑巨型框架承担较多的弯矩。图7为结构的剪力分配图。由图可知，除底部少数楼层外，其它楼层带斜撑巨型框架与核心筒分担的剪力沿高度变化不大，近似为一定值，外筒承担了大多数剪力，与内外筒抗剪刚度之比完全相反；在结构底部少数楼层，带斜撑巨型框架承担的剪力从上到下依次减小，内部核心筒承担的剪力依次增大。除了在楼层底部和设置环带桁架处，本文方法得到的内外筒剪力与有限元得到的剪力基本一致。本文用哈密顿力学的方法对结构进行协同分析时采用了连续化假设，得到的内外筒的剪力是连续的，采用有限元得到的楼层剪力在环带桁架处存在剪力突变。带斜撑巨型框架－核心筒结构与传统的框架筒体结构受力机理不同，外部巨型框架承担了较多的弯矩和剪力。

图7 内外筒剪力分配Fig.7 Shear distribution of inner and outer tube and outer tube

4.3 结构内力、变形影响因素分析

抗剪刚度和抗弯刚度对结构的侧向变形和结构内力影响较大。斜撑可提高结构的抗侧刚度以及整体稳定性，控制其它参数不变，改变斜撑的横截面尺寸探讨对结构侧向变形以及内力的影响，将斜撑横截面尺寸由原来的1800 mm×900 mm×50 mm× 150 mm 改 变 为1800 mm × 1800 mm ×200 mm×200 mm、900 mm×900 mm×150 mm×150 mm。

由表2 中的数据可得到，改变斜撑的面积对结构顶点侧移和弯矩分配影响较小，但是对剪力分配影响较大。巨型斜撑面积越大，在侧向荷载作用下外部带斜撑巨型框架承担的剪力就越多。

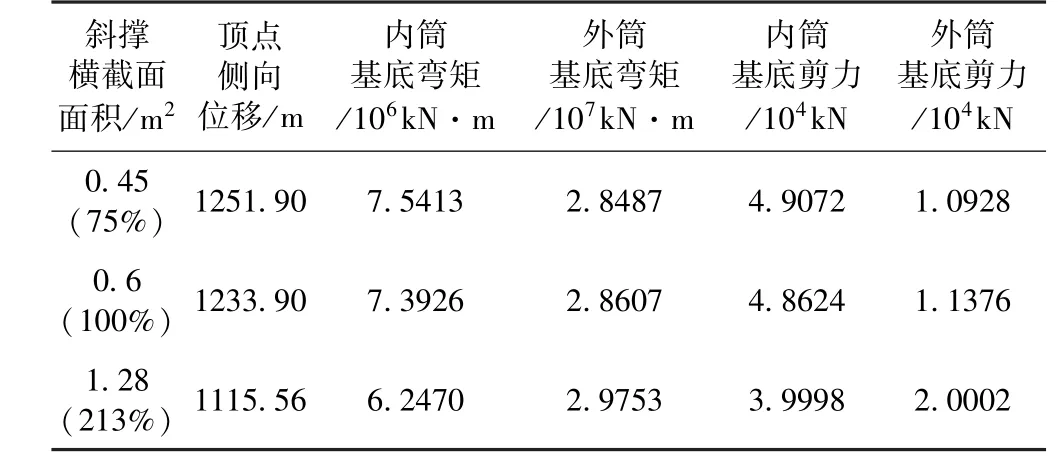
表2 结构内力、位移对比Table 2 Comparison of internal force and displacement of structure

5 结论

（1） 本文将带斜撑巨型框架与核心筒分别等效为底端固定、上端自由的悬臂梁，悬臂梁有弯曲变形和剪切变形，建立带斜撑巨型框架－核心筒计算模型。用哈密顿力学对带斜撑巨型框架－核心筒结构进行分析，导出哈密顿对偶体系，用精细积分法进行求解，具有概念清晰、推导过程简单、计算简捷等特点，避免了传统方法复杂的理论推导。针对带斜撑巨型框架－核心筒协同分析提出了一种新的计算方法，并通过工程案例，与参考文献以及有限元的计算结果进行对比分析，验证本文方法的可行性。

（2） 超高层结构自由度较多，计算分析工作量较大。对结构采用简化模型分析时，计算简便，同时可以快速把握结构的整体受力性能。本文采用哈密顿力学的方法对带斜撑巨型框架－核心筒结构进行简化分析，可以准确把握结构协同工作的性能，可用于初步设计阶段时对结构方案进行快速受力分析。

（3） 计算结果表明，水平荷载作用下，带斜撑巨型框架－核心筒变形呈“弯曲型”； 除结构底部少数楼层外，带斜撑巨型框架和核心筒分担的剪力沿高度变化不大； 在结构底部少数楼层，带斜撑巨型框架的剪力逐渐减小，内部核心筒的剪力逐渐增大； 斜撑面积越大，水平荷载作用下外部巨型框架承担的剪力越多。