SOLO分类理论下小学数学作业设计与评价

李术伟 倪婧倩 刘银 刘洪艳

摘  要：“双减”背景下，作业更需要指向学生的素养发展。从“教”和“学”的角度来看，作业是课堂学习的巩固、补充和延伸；从“评”的角度来看，作业是教师评估学生、诊断教学的重要依据。而SOLO分类理论是一种量的测评与质的考查相结合的评价理论，恰当运用该理论将作业设计融入单元整体教学中，可以有效帮助教师明确学生的思维发展水平及层次，诊断和优化教师的“教”与学生的“学”。

关键词：SOLO分类理论；因数和倍数；作业设计

一、SOLO分类理论在作业设计中的价值

“因数和倍数”的作业设计与评价主要采取SOLO分类理论，把学生的认知水平由低到高划分为五个层次：1. 前结构。学生基本上无法理解问题和解决问题，或者被材料中的无关内容误导，回答问题逻辑混乱。2. 单点结构。学生在回答问题时，只能涉及单一的要点，找到一个解决问题的线索就立即跳到结论上去。3. 多点结构。学生在回答问题时，能联系多个孤立要点，但这些要点是相互孤立的，彼此之间并无关联，未形成相关问题的知识网络。4. 关联结构。学生在回答问题时，能够联想问题的多个要点，并能将这多个要点联系起来，整合成一个连贯一致的整体，说明学生真正理解了这个问题。5. 抽象拓展结构。学生在回答问题时，能够进行抽象概括，从理论的高度分析问题，而且能够深化问题，使问题本身的意义得到拓展。

針对课时作业评价，采用该方法不仅可以考查学生知识与技能的目标是否达成，还可以诊断学生的思维发展水平，并结合具体的发展情况采取后续的辅导措施。

二、SOLO分类理论实现“教学评”一致性

例如“因数和倍数”教学。首先需要将所学内容的核心、内容所蕴含的思想方法及教育价值确立为学习主题，形成本单元具体概念，以统领整个单元的学习。在此基础上形成单元教学目标，再细分到每课时目标。这是从“教”的角度去做。从“学”的角度来看，还要将课业目标与之对应，以SOLO分类评价为载体，优化学生思维水平保证“教学评”的一致性。

（一）单元解析提炼目标

单元主题：理解并应用整除关系。

具体概念：

1. 质数、合数、奇数、偶数、公因数、公倍数都是以“因数和倍数”为基础研究的，都是对数与数之间关系的一种描述。

2. “因数和倍数”是建立在整数除法的基础上，可以丰富对数的关系的认识。

3. 直观操作不仅可以帮助学生理解数的关系，还可以发展推理能力。

4. 运用“因数和倍数”的知识解决生活中简单的数学问题，发展应用意识。

（二）结合目标细化学习结果表现

“因数和倍数”是建立在小学生对数与数之间的关系有了一定了解的基础上进行的一次深入学习，这些数与数之间的关系可见表1。

三、重点课时作业设计

（一）核心课对应关键作业

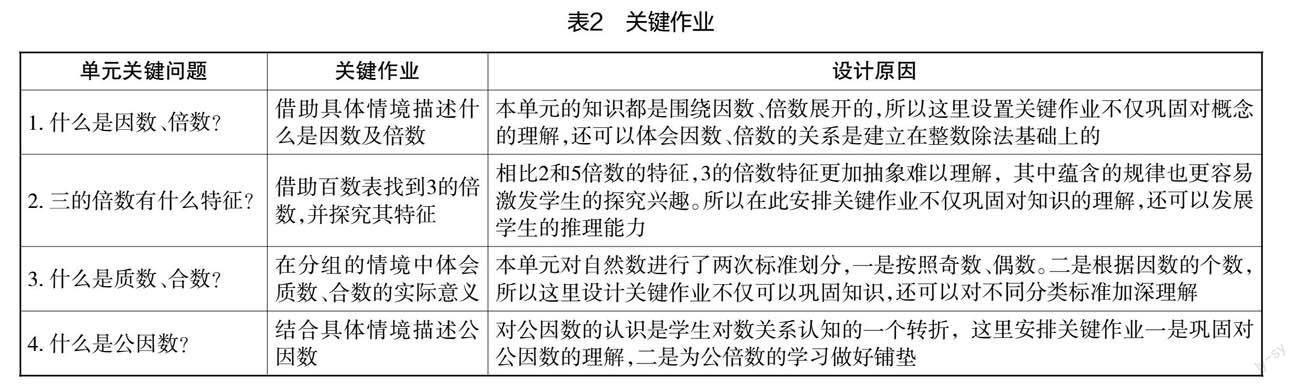
“因数和倍数”对小学生掌握数与数之间的关系非常重要，这种核心课所对应的即为关键作业，可见表2。

（二）重点课时作业举例

1. “认识因数和倍数”

（1）老师拿来36个苹果，让同学们把苹果放入盒子里，不许一次放完，也不许一个一个放，每次放的个数相同且没有剩余，共有几种放法？结合刚才的思考说一说你对因数、倍数有哪些新的理解。

（2）你认为下面（  ）选项中的两个算式中的两个数具备因数和倍数关系。

A. 12÷3=4；5×6=30 B. 24÷4=6；3.5÷7=5

C. 2.1×5=10.5；7×7=49 D. 36÷4=9；47÷5=9…2

不是的有（  ），理由是：____________________。

2. “3的倍数特征”

（1）“观察百数表，请你在3的倍数上画‘○，观察3的倍数有什么规律？为什么有这样的规律？试着说明理由。”

（2）“判断一个数是不是2或5的倍数，只需要看个位数字，而判断一个数是不是3的倍数，却要看各个数位上数字的和，这是为什么呢？请你观察下列算式的特点，然后写出自己的想法。”

24=20+4

2345=2340+5

24=2×10+4=2×（9+1）+4=2×9+2+4

2345=2×1000+3×100+4×10+5

=2×（999+1）+3×（99+1）+4×（9+1）+5

=2×999+3×99+4×9+2+3+4+5

我认为原因是：_____________________________。

四、SOLO分类评价度量学习层次

依据SOLO分类的五个层次与大多数的评价方式有比较类似的地方（见表3），例如：了解层次的表现是只能进行简单的作答，而理解不仅可以正确作答，还可以进行正确的表述，对接SOLO分类评价水平一、二。应用层次表现为可以正确解答简单的实际问题。但是和迁移的区别在于后者可以进行举例说明，对接SOLO评价的水平三、四。联系层次的表现为可以进行正确推理、抽象，对接SOLO评价水平四、五。

例如“公因数”课时作业设计中的第3题，借用SOLO分类理论的评价会呈现以下几个水平层次。

1. 前结构：学生不会解答，不能将所学知识运用到实际的生活情境中。

2. 单点结构：学生会分别找到“72和36”“24和36”“72和24”的因数，但是彼此的公因数没有建立联系。

3. 多点结构：能够找到两条边的最大公因数，或三条边的某个公因数，并且明确表述这个题是计算最大公因数。

4. 关联结构：能够找到三个数的最大公因数，并且通过画图或者举例说明计算最大公因数的道理。

5. 抽象拓展结构：通过举例说明公因数或最大公因数与除法之间的联系。

结合具体的占比情况，可以判断这节课学生的整体思维发展水平。比如更多的数据反映在单点结构，说明教师授课方式有待改进。多点结构较多说明教师可以利用各种支架引导学生主动参与学习，唯独在联系方面做得比较欠缺。可以判断教师基本上能够做到以学生为中心，可能对知识的理解或者对生成处理方面欠缺。如果大部分学生处于这个水平说明教师处在成长期；如果个别学生处在这个水平，则提示教师课后辅导时应引导学生对知识间的联系多练习。如果大部分学生处于关联结构，除了说明这节课非常透彻，还可能说明教学设计出现了问题，没有使学生进入深度学习状态，当然这个联系还要看是否有价值。

这只是针对某个题目进行的剖析，如果是两个班的水平测试则可以反映出哪个班的思维水平高。例如在总分数相等的情况下，哪个班的四、五层次占比高则表明哪个班的学生思维好，同时反映教师日常教学的理念及授课水平高。在评价的过程中，对处于不同SOLO水平的学生，评价的侧重点应有所不同，积极回应学生的学习需求，满足不同学生的学习期待，促进学习进阶。

参考文献：

［1］刘徽. 可观察的学习结果结构——读《学习质量评价：SOLO分类理论》［J］. 现代教学，2020（21）：77-79.

［2］张祥文. 《学习质量评价：SOLO分类理论（可观察的学习成果结构）》简介［J］. 地理教学，2016（15）：1.

［3］毛文波. 切片分析：小学数学教材分析新路径——以“因数和倍数”为例［J］. 教师教育论坛，2022，35（04）：41-44.

（责任编辑：邹宇铭）