基于随机森林和随机游走的交互式图像分割

吕律

摘要：基于随机游走的交互式图像分割在计算相邻像素相似度时，仅考虑了颜色空间的差异。针对这一问题，利用图像中广泛存在的对称结构，提出一种基于随机森林进行对称检测的方法。通过基于相似边的特征，将对称检测转化为结构化标签问题。在得到对称轴的基础上，通过期望最大算法，建立对称轴与相邻像素之间的关系，以提高交互式分割的精确度。实验表明，该方法不仅能有效地提取图像中的对称轴，而且能得到较高精度的交互式分割结果。

关键词：交互式图像分割；随机森林；随机游走；对称检测；期望最大算法

中图分类号：TP391.41        文献标识码：A

文章编号：1009-3044（2023）31-0014-04

开放科学（资源服务）标识码（OSID）

0 引言

图像分割是图像处理的基础性问题，是图像理解的基石，可以被应用于自动驾驶系统中的街景识别与理解，無人机系统中的着陆点识别[1]。近几年基于深度学习的语义分割（semantic segmentation） ，即对图像中表达的语义（不同的物体）进行分割，取得了很高的精确度[2]。但是对于下面2种情况，如果没有人的交互，还是很难达到满意的效果。1） 在背景比较杂乱的情况下，图像中的物体有很多细小的枝节（如图1中的鹿角）；2） 需要将物体的不同部分进一步划分（如图1的鹿头和黑色的颈部划分为同一个部分）。交互式图像分割正是研究解决这一类问题的方法。

交互式图像分割与图像分割的区别在于，需要人在图像中用不同颜色标注出需要分开的区域[3]，如图1中不同颜色的点（黄色和绿色点），下文称之为交互点。因为深度学习是一种端到端的学习方法，现有的深度学习方法还没办法处理交互点这种先验知识[4]。现有文献也没有采用深度学习方法进行交互式图像分割，所以本文提出的是一种基于随机游走（random walk） 的方法。

现有基于随机游走的交互式图像分割方法是一种非监督的分割方法，根据图像中相邻像素的相似度计算转移概率矩阵，当随机游走达到稳定时，得到图像中的像素所对应的人工标注[1]。虽然图像分割是一种非监督的问题，但是利用图像中的对称结构，可以提高分割的效果。如图1所示，人工标注的点，落在了对称区域（鹿角的主干，鹿的颈部），该区域可以作为人工标注处理，与该区域相邻点的相似度也应该相应提高。所以将人工交互点扩展到这些交互点所在的对称区域，直观上通过增加了交互点的数量，应该能提高分割的精度。现有的交互式图像分割文献，并没有利用图像中的对称性进行分割，于是本文提出一种基于对称区域改进现有的随机游走方法，并通过实验表明比现有方法的结果更好。

对称检测在图像处理中不是一个热门的研究领域，相关的文献比图像分割要少得多[5]。这些研究的共同特点是提出不同的图像特征，基于这些特征计算图像中的对称轴。现有的数据集SYMMAX-300[5]，数据量很小，不适合深度学习方法（关于利用深度学习方法处理交互式图像分割和对称检测，本文在最后一节结束语，作为未来的研究进行讨论）。通过仔细分析这些文献中的图像特征，可以发现现有方法并没有考虑对称区域的边界的相似性（如图2（a） 边ab与cd） 。本文提出的方法利用相似边界等多种特征，改进了随机森林算法进行对称检测，最后通过实验证明，比现有方法的结果更好。综上所述本文的工作有以下2点：1） 通过图像中的相似边等多种特征，改进随机森林算法得到对称轴；2） 利用对称区域，改进随机游走算法得到图像的分割区域。

1 基于随机森林的对称检测

本节首先介绍现有的对称检测方法，然后介绍本文改进的对称检测方法。

1.1 现有对称检测方法

在现有关于对称检测的文献中，SYMMAX-300[5]是广泛被使用的数据集。这些研究的共同特点是通过以下2步检测图像中的对称信息：1） 提取不同的图像特征；2） 基于标注了对称信息的数据集和1中提取的特征，通过不同的学习算法得到对称模型。现有文献中用的特征主要有：尺度不变特征变换（Scale-invariant feature transform，SIFT） 特征：图形的颜色、材质等特征。其中Tsogkas等人提出的一种专门针对对称问题的直方图特征[5]，因为1.2节本文方法用到了这种特征，所以简要介绍一下。

以图像中的点（x，y）为中心作边长为a的正方形区域，并分割成三个相邻的面积相等的矩形，即矩形的边长为a和a/3。对于任意两个矩形，可以定义相异度函数[DHi，j（x，y）]（该相异度函数就是直方图特征）：

[DHi，j=12t（Ri（t）-Rj（t））2Ri（t）+Rj（t）]            （1）

其中，[i，j∈{1，2，3}]表示三个矩形的标号。[Ri]、[Rj]分别表示矩形i和矩形j区间中的直方图（histogram） ，t是直方图中的分组数，实验中t=64。

1.2 基于随机森林的对称检测

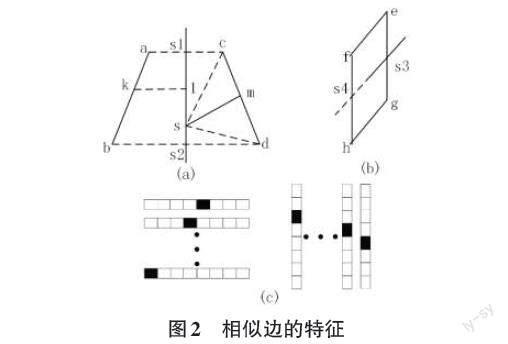
从前面对直方图特征的介绍可以知道，因为计算的是矩形区域，所以现有方法没有考虑到对称区域的边界是相似的（图2（a） 中边ab，cd，中间的实线是对称轴），并且相似边到对称轴区域的颜色，材质是相似的（图2（a） 中区域abs2s1，区域cds2s1） 。本节方法的第1个贡献是提出多种基于相似边的特征。随机森林是利用多种特征进行分类、回归较好的方法[6]，但是对称轴是1条曲线（图2是示意图，简化为直线），不是简单的分类数值，或者回归数值，本节方法的第2个贡献是提出一种方法，改进随机森林，计算对称轴这种结构化的目标。

1） 基于相似边的特征。现有的数据集（SYMMAX-300） 只包含对称轴信息，如果人工提取对称轴相应的相似边数据，不仅困难而且非常费时。所以，本方法利用相似边与对称轴的关系，去掉明显不相似的边，从而得到基于相似边的特征。

图2（a） （b） 是数据集中2种主要的对称模式，相似边（ab，cd） 反转对称，相似边（ef，gh） 平移对称，对称轴窗口取8×8像素，所以对称轴都是弧度较小的曲线或者近似的直线。首先构造候选区域，先通过现有边缘检测方法提取对称轴两侧的边，下文称之为候选边，分别连接候选边的两个端点得到两条直线（ac，bd） ，对称轴至少要与其中1条相交。当与两条直线相交时（如图2（a）） ，区域abs2s1和区域cds2s1是候选区域；当只与1条直线相交时（如图2（b） 中间实线是对称轴，虚线是延长线），区域efs4s3和区域ghs4s3是候选区域。候选区域的面积是第一种特征。

过候选边上一点（如图2（a） 点k） 做垂直于对称轴的线段作为距离di（如图2（a） kl） ，平均距离[d=i∈Edi/|E|]是第2种特征，其中，[i∈E]表示边E上所有的点，|E|表示边上所有点的个数。

将候选边所在窗口（8×8像素）中的边自上而下扫描，每1行向左和向右扩大1个像素，即将边变粗，变粗后的边的面积为S1和S2。该面积是第三种特征。

将不满足下面三个条件的候选边去掉，剩下的就是相似边：

[|A1-A2|min{A1，A2}<20% ，       |d1-d2|min{d1，d2}<20% ， ]

[max{S1⋂S2}min{S1，S2}>70%]   （2）

其中，A1、A2表示对称轴两侧候选区域的面积，d1、d2表示对称轴两侧候选区域的平均距离，[max{S1⋂S2}]表示S1、S2分别反转和不反转共4种情况下最大的相交的面积。

训练模型时，对称轴是已知的。但是测试时，对称轴是要计算的目标未知。这时已知的是8×8像素区域，计算对称轴是否在这个区域。分别连接候选边的2个端点构造直线L1、L2，然后连接L1和L2的中点，以这条线为对称轴，并通过（2） 式中3个条件得到相似边。

通过（2） 式去掉不相似的候选边后，剩下的候选边即相似边，该相似边对应的候选区域即为对称区域。连接相似边的中点和对称轴上任一点的距离记为ds（如图2（a） 中ms的距离），这是第4种特征。ds与水平线的夹角[α]是第5种特征。分别连接相似边两个端点和对称轴上任一点围成的区域是第6种特征（如图2（a） 中区域csd） 。基于第6种特征区域，可以得到相应的颜色，材质的直方图特征（第7种特征），即[DHLi，j]、[DHai，j]、[DHbi，j]、[DHti，j] （其中L、a、b分别是CIELAB颜色空间中的L、a、b信息，t是材质）。材质t的计算采用文献[7]中的方法。

2） 计算对称轴。前面已经介绍了对称轴（如图2（a）） 所示是一条曲线，既不是分类数值，也不是回归数值。通过分析对称轴数据集，可以发现非水平对称（如图2（a） 所示）的情况下，每行只占1个像素值。水平对称是指对称轴是一条水平线，这时每列只占一个像素。图2（c） 将对称轴所在的8×8像素目标区间按行分为8行，或者按列分为8列。所以计算对称轴相当于在每一行（或者一列）8个像素中找出对称轴的那个像素，即分类问题。于是可以将对称轴所在区域（8×8像素）分为按行或者按列划分两种情况，每种情况根据不同的行（列）建立相应的随机森林模型。下面，首先给出按行或者按列进行计算的判定条件。

训练时，因为对称轴是已知的，连接对称轴两个端点所得直线与水平线的夹角[β]，[β>20°]按行计算，否则按列计算。测试时，因为对称轴未知，连接相似边两个端点所得直线与水平线的夹角[γi]，[i∈SEγi/|SE|>20°]按行计算，否则按列计算，其中[i∈SE]表示该对称轴对应的所有相似边，|SE|表示相似边的个数。

对于第i行（或者第i列），针对不同行（列）构造相应的特征。基于第3、4、5、6、7种特征，构造随机森林中每一个节点的函数：

[h（x，θj）=[f（x，k）<τ]， θj=（k，τ），k=3，4，5，6，7f（x，3）=max{S1⋂S2}min{S1，S2}， f（x，4）=|ds1-ds2|min{ds1，ds2}，f（x，5）=|α1-α2|min{α1，α2}， f（x，6）=|AS1-AS2|min{AS1，AS2}，f（x，7）=DH*i，j， *=L，a，b，t]   （3）

其中，[.]是指示函数，[τ]表示阈值，k对应第几种特征。训练决策树时，对于一个节点和训练集[Sj⊂X×Y]，目标是找到[h（x，θj）]中的[θj]能够很好地将数据进行划分。数据划分的标准是信息增益：

[Ij=H（Sj）-k∈{L，R}SkjSjH（Skj）]   （4）

其中，[SLj={（x，y）∈Sj|h（x，θj）=0}]，[SRj=Sj＼SLj]，[H（S）=-ypylog（py）]，py表示S中標记为y的概率。通过最大化Ij可以计算出[θj] 。

2 基于随机游走的交互式图像分割

本节介绍利用前面得到的对称轴与相似边，对传统随机游走模型进行改进。

Grady对于交互式图像分割问题，首先提出随机游走算法[8]。他通过无向图[G=（V，E）]对图像进行建模，其中节点[v∈V]，边[e∈E⊆V×V]。每一个节点[vi]代表图像像素[xi]，边[eij]表示[vi]与其相邻的8个节点[vj]构成的边，[wij]表示随机游走通过边[eij]的权值。

[wij=exp（-||Ii-Ij||2σ）]   （5）

其中，[Ii]和[Ij]分别表示节点[xi]和[xj]对应于CIELAB颜色空间的值。实验中[σ]是控制参数，令[σ=22]。D是对角矩阵，其中[Dii=di]，[di=j～iwij]表示节点[vi]的度， [i～j]表示与[vi]相邻的节点[vj]。因为在第1节计算得到对称轴和相似边，当交互点落在对称区域（图2（a） 区域abdc） ，该区域的所有点被作为交互点处理（即具有相同的标签）。并将对称区域的面积（区域中的像素个数）增大1倍，相应区域记为V，区域V中节点[vi]到[vj]的权值计算如下：

1） 基于第1节计算的对称区域，得到的直方图作为初始值，通过期望最大算法（Expectation maximization） [9]计算对称区域对应的标签k的均值[μkt]，方差[θkt]和先验概率[πkt]，t是直方图分组数，实验中t=64。

2） 对于区域V中的每一个像素[Ii]，对每一个分组t，计算：

[Jkit=-logπkt+0.5×（log|θkt|+Ii-μktθkt）]   （6）

其中，[|θkt|]是[θkt]的行列式的值。

3） 对于全部分组t，[mintJkit]表示同一k值下，取最小的[Jkit]，[100-mintJkit]为了方便计算，[Ji=maxk{100-mintJkit}] ，[gij]表示节点[vi]到[vj]的权值：

[gij=exp（-||Ji-Jj||2σ）]  （7）

其中，G是对角矩阵，其中[Gii=gi]，[gi=j～igij]。（7） 式与（6） 式相同，只是将I换成J，实验中令[σ=22]。

所以图像中任意两点i，j的转移概率为

[q（i，j）=ci，当i=j（1-ci）gijGi，当j～i∈V（1-ci）wijDi，当j～i∉V0，其他情况]   （8）

其中，ci表示，当i=j时，当前点转移回自己的概率，参考文献[10]，实验中令ci=c=0.000 4。设随机游走从第m个交互点[xlkm]（其标记为lk） 开始，[rlkim]表示随机游走达到稳定态时停在xi的概率，

[rlkim=（1-ci）j～i∈VrgijGirlkjm+（1-ci）j～i∉（Vr，V）wijDirlkjm+ciblkim]  （9）

其中，[blkim=[bi]N×1]，当[xi=xlkm]，[bi=1]，其他情况，[bi=0]。所以每个节点的标签实际是求（10） 式：

[Ri=argmaxlkrlki]   （10）

其中，[rlki=[rlkim]N×1]，即每个节点对应的标记的最大值。

3 实验结果与分析

本节首先测试第1节中对称检测算法，并与现有方法进行比较；再测试本文所提出的交互式图像分割算法，并与现有方法进行比较。

3.1 对称检测实验

本节对称检测采用SYMMAX-300数据集[5]，该数据集是在BSDS-300[7]的基础上手工加上对称轴信息，并广泛应用于对称检测中。测试的标准采用文献[11]中的ODS（Optimal Dataset Scale） ，OIS（Optimal Image Scale） 和AP（Average Precision） 。ODS是对整个数据集的一个最优尺度下的F值度量（F-Measure） 。OIS是对每一幅图像在最优尺度下的F值度量。F值度量计算如下：

[F值=2×正确率×召回率正确率+召回率]  （11）

其中，正确率=（计算得到的正确数目）/（计算得到的数目），召回率=（计算得到的正确数目）/（样本的数目），AP是平均正确率。

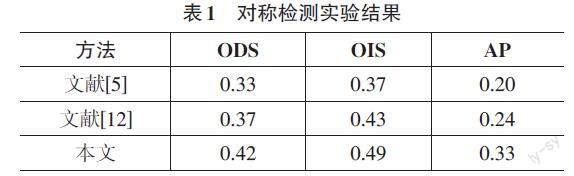
本节将第1节中方法与文献[5]和[12]进行比较，见表1。其中第1节用到的直方图特征就是文献[5]提出的。只比较了两种相关的方法的原因有两个：1） 现有对称检测的文献中，很多论文的结果是定性的，如图3所示，从图中比较结果，于是本文实现了文献[5，12]的方法并进行比较；2） 本文的目的是交互式图像分割，有些对称信息如图3（a） 人体和草裙上的人工标注的对称轴对图像分割作用不大，所以在交互式图像分割实验部分与更多其他方法进行比较，见表2。如表1所示，很明显本文方法在3个标准比文献[5]和 [12]都好。但是本方法3个标准的值还是比较低，原因如图3所示。图3（a） 是手工标注作为测试的真实值，但是很明显图中人的背部，草裙中的分叉是否对称轴，是有争议的，对图像分割的作用不大，本方法并不计算这种分叉。图3（b、c、d） 给出文献[5]、[12]和本方法的实例。

图3（b） 是采用文献[5]方法，因为没有考虑相似边因素，很多边界也被计算为对称轴，比如图左上的塔除了中间的对称轴，还将左右两条边界也误判为对称轴。图3（c） 是采用文献[12]方法，该方法基于一种可变形的圆盘（deformable discs） 来描述对称区域，但是图3（c） 中右边一些树林也被认为是对称结构。图3（d） 是本文方法，除了人物背部和草裙上有争议的对称轴，本方法将湖水的一部分判断为对称轴，虽然这可能不是对称轴，但是对于图像分割是有意义的。

3.2 交互式图像分割实验

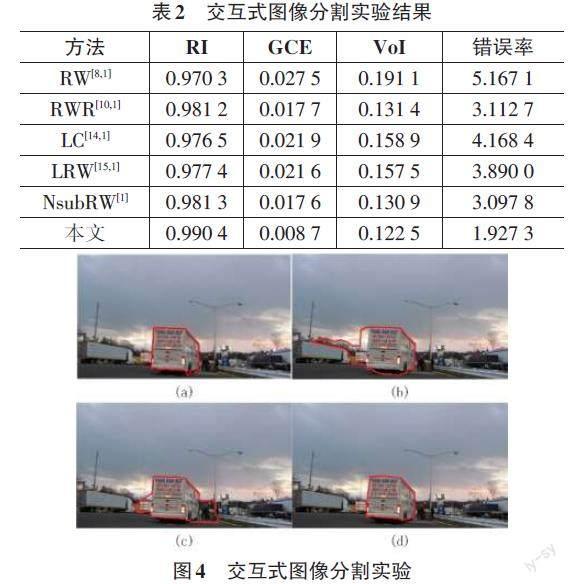
交互式图像分割实验，采用的是GrabCut数据集[13]，该数据集广泛地应用于交互式图像分割中[3]。这里将本文方法与RW[8]、RWR[10]、LC[14]、LRW[15]、NsubRW[1]进行比较，结果见表2。其中，RW、RWR、LC、LRW的结果摘自文献[1]，因为文献[1]将文献[8，10，14，15]的方法都實现了，而且文献[1]发表在图像处理的重要期刊IEEE TRANSACTIONS ON IMAGE PROCESSING。测试标准采用的是文献[14]中的RI（Rand Index） ，GCE（Global Consistency Error） ，VoI（Variation of Information） 和错误率。RI统计分割结果与手工标注具有相同标签像素对的个数，是一个比值，取值范围[0，1]，取值越大，分割效果越好。GCE计算分割结果与手工标注，其中一个能否看作另一个细化后得到的程度，取值范围[0，1]，取值越小，分割效果越好。VoI计算分割结果和手工标注之间的相对熵，取值越接近0，分割效果越好。错误率就是被错误标注像素的百分数，取值越低，分割效果越好。

通过表2的比较，很明显因为加入了对称轴信息，本文方法在4个标准都比现有方法要好。本文实现了RWR[10]和LRW[15]方法，图4是分割实例。图4（a） 是手工结果，图4（b） 是LRW结果，图4（c） 是RWR结果，图4（d） 是本文方法。很明显RWR和LRW，因为没有考虑图像中对称信息，将汽车周围的一些区域也一起分割了。对比本文方法图4（d） 和手工结果图4（a） 可以发现，只有汽车右下部分涉及轮胎的部分存在差异。

4 结论

本文通过计算图像中的对称信息，改进传统基于随机游走的交互式图像分割方法，得到更精确的分割结果。本文对现有的对称检测方法也进行了改进，提出基于相似边的特征，并提出一种通过随机森林学习结构化目标的方法，实验证明该方法比现有方法得到更精确的对称轴。

未来的工作有2个方向：1） 因为对称检测的数据集比较小，改进深度学习方法，使其能适用于数据集小的领域，这个也是深度学习一个研究方向；2） 因为交互式图像分割，涉及交互点这种先验知识，将先验知识融入深度学习方法，这个也是深度学习一个研究方向。

参考文献：

[1] BAMPIS C G，MARAGOS P，BOVIK A C.Graph-driven diffusion and random walk schemes for image segmentation[J].IEEE Transactions on Image Processing，2017，26（1）：35-50.

（下转第21页）

（上接第17页）

[2] PAPANDREOU G，CHEN L C，MURPHY K P，et al.Weakly-and semi-supervised learning of a deep convolutional network for semantic image segmentation[C]//2015 IEEE International Conference on Computer Vision （ICCV）.IEEE，2016：1742-1750.

[3] SPINA T V，DE MIRANDA P A V，Xavier Falcão A.Hybrid approaches for interactive image segmentation using the live markers paradigm[J].IEEE Transactions on Image Processing，2014，23（12）：5756-5769.

[4] REZENDE D J，MOHAMED S，WIERSTRA D.Stochastic backpropagation and approximate inference in deep generative models[J].31st International Conference on Machine Learning，ICML 2014，2014，4：3057-3070.

[5] TSOGKAS S，KOKKINOS I.Learning-based symmetry detection in natural images[M].Computer Vision – ECCV 2012.Berlin，Heidelberg：Springer Berlin Heidelberg，2012：41-54.

[6] GEURTS P，ERNST D，WEHENKEL L.Extremely randomized trees[J].Machine Learning，2006，63（1）：3-42.

[7] MARTIN D R，FOWLKES C C，MALIK J.Learning to detect natural image boundaries using local brightness，color，and texture cues[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2004，26（5）：530-549.

[8] GRADY L.Random walks for image segmentation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2006，28（11）：1768-1783.

[9] BISHOP， CHRISTOPHER M.Pattern Recognition and Machine Learning[M].Springer New York，2006.

[10] KIM T H，LEE K M，LEE S U.Generative image segmentation using random walks with restart[M]//Lecture Notes in Computer Science.Berlin，Heidelberg：Springer Berlin Heidelberg，2008：264-275.

[11] ARBELAEZ P，MAIRE M，FOWLKES C，et al.From contours to regions：an empirical evaluation[C]//2009 IEEE Conference on Computer Vision and Pattern Recognition.IEEE，2009：2294-2301.

[12] LEE T S H，FIDLER S，DICKINSON S.Detecting curved symmetric parts using a deformable disc model[C]//2013 IEEE International Conference on Computer Vision.IEEE，2014：1753-1760.

[13] ROTHER C，KOLMOGOROV V，BLAKE A.“GrabCut”：interactive foreground extraction using iterated graph cuts[C]//SIGGRAPH '04：ACM SIGGRAPH 2004 Papers.New York：ACM，2004：309-314.

[14] CASACA W，NONATO L G，TAUBIN G.Laplacian coordinates for seeded image segmentation[C]//2014 IEEE Conference on Computer Vision and Pattern Recognition.IEEE，2014：384-391.

[15] SHEN J B，DU Y F，WANG W G，et al.Lazy random walks for superpixel segmentation[J].IEEE Transactions on Image Processing，2014，23（4）：1451-1462.

【通聯编辑：唐一东】