矩阵奇异值分解算法在图像处理中的应用
2023-12-25张继龙曹石
张继龙 曹石





摘要:随着互联网技术的飞速发展,矩阵分解尤其是矩阵奇异值分解在图像处理、信号处理以及神经网络等领域有着广泛应用。针对图像处理问题,文章首先给出了奇异值分解的基本理论,随后分别介绍了奇异值分解应用于图像压缩及数字水印技术的基本原理并进行Matlab应用实现,最后构建了数据分析模型并进行了数值实验综合分析,将图像处理的几类应用结合实现了综合性的图像处理程序。
关键词:矩阵分解;奇异值分解;图像压缩;低秩逼近;数字水印
中图分类号:TP18 文献标识码:A
文章编号:1009-3044(2023)31-0001-04
开放科学(资源服务)标识码(OSID) :
0 引言
奇异值分解是特征分解在任意矩阵上的推广,在互联网技术发展后广泛运用于解决各类实际问题,其中图像处理问题是奇异值分解最具有代表性的应用场景之一。目前使用的图像都是以数据形式进行存储,对数据存储的高要求使得在尽可能保持图像清晰度的前提下减少图像存储空间,具有一定应用价值,而使用低秩逼近的方法进行图像压缩是一种在获得相同压缩比的前提下误差较小的方法,能够取得不错的效果。
然而本方法在实际应用中依旧需要进一步获取更多信息来平衡图像清晰度和数据大小,数字水印是一种在图像中嵌入信息的算法,同样可以使用奇异值分解来进行处理。添加数字水印后进行图像压缩,之后再将水印提取,通过对比压缩前后水印的相似度可以用于评估压缩图像后图像信息的损失程度,以此来得到代表图像清晰度的数据。在此基础上,通过压缩比以及图像清晰度构建模型评估压缩质量,以此在低秩逼近图像压缩算法的基础上,进一步得到更具备实用性的图像压缩结果。
综上所述,文章在利用奇异值分解低秩逼近图像压缩的基础上,进一步结合数字水印技术来构建评估模型进行数据分析论证,得到了一种更具有实用价值的图像压缩处理方法,细化了图像压缩程序的应用实现,对该方法的应用进行了进一步的深入研究。
1 奇异值分解基本理论
1.1 奇异值分解定义[1-2]
定义矩阵的奇异值,对[A∈Cm×nr],记[AAH]的特征值为[λi],[AHA]的特征值为[μi],可以通过直接计算得到[δi=λi=μi],[δi]称为[A]的奇异值。
对[A]进行奇异值分解:记[δ1≥δ2≥…≥δr>0]是[A]的r个正奇异值,则存在使得[A=UDVH=UΔ000VH]成立的m阶酉矩阵[U]和n阶酉矩阵[V],式子中的[Δ=diagδ1,δ2,...,δr]为正奇异值为对角元的对角阵。
1.2 奇异值分解求解步骤
1) 通过求矩阵[AAH]的特征值[λi],计算对应的奇异值[δi],得到[Δ=diagδ1,δ2,...,δr],計算[AAH]的特征值及特征向量,标准正交化后得左奇异矩阵[U]。
2) 由[A=UDVH]得[VH=D-1UHA],此即[V=AHUD-H]。
3) 奇异值分解的形式为[A=UDVH]。
2 基于奇异值分解的图像压缩原理
2.1 利用低秩逼近的图像压缩方法
设[A∈Cm×nr],[A]的奇异值分解形式为[A=UDVH],可以将分解形式改写为:[A=UD1+D2+...+DrVH],其中[Dk=Δk000,Δk=diag(0,...,δk,...0)],这样就将[A]分解为了r个秩为一的矩阵之和,设[Ak=UD1+...+DkVH],则[Ak]是矩阵[A]的低秩逼近,对于图像来说,只需要将其图像信息读取为数据矩阵就可以通过低秩逼近来进行压缩。
由矩阵[A]的Frobenius范数(F-范数)的酉不变性,[A]的F-范数[||A||F=||UDVH||F=||D||F=δ21+δ22+...+δ2r],因此该方法可以表示为如下最小二乘问题:[minrankB=k||A-B||F=||A-Ak||F=δ2k+1+...+δ2r],由于矩阵奇异值[δ1≥δ2≥...≥δr>0],而往往其中前10%甚至更少的奇异值之和就能达到总和的90%以上[3],少量奇异值就可保存较多信息,因此使用该方法进行图像压缩可以取得较良好的效果。
2.2 通过Matlab实现的算法实例
1) 读入图像数据,对于彩色图像需要进行灰度化处理使其变成矩阵的形式。
将该图片命名为test.jpg,分辨率为4 160×3 120,首先读取图像信息:
A = imread('D:\examset\test.jpg');%将图像信息存储为数据矩阵A,A为3 120×4 160×3,3代表为彩色图像
对A进行灰度化处理:
A_gray=rgb2gray(A);%经过灰度化处理后的A_gray为3 120×4 160的灰度矩阵
[m,n]=size(A_gray);%m为行数,n为列数
2) 设置压缩比[ρ=mnkm+n+1][4],[k]为保留的奇异值个数,[k]越小压缩比越大,压缩后占空间大小越小,清晰度也越低。
k1=20;k2=40;k3=60;k4=80;%设置k值间隔
rho1=m*n/(k1*(m+n+1));rho2=m*n/(k2*(m+n+1));
rho3=m*n/(k3*(m+n+1));rho4=m*n/(k4*(m+n+1));%计算压缩比
根据本例设置的k值以及选取的图像大小,计算得到的压缩比分别为rho1=89.130 6,rho2=44.565 3,rho3=29.710 2,rho4=22.282 7。
3) 将灰度化矩阵作奇异值分解,低秩逼近后对灰度矩阵进行重构,读取压缩图像。
A_gray1=double(A_gray);%将灰度矩阵转换为double型
[U,S,V]=svd(A_gray1);%奇异值分解
S1=diag(S);S2=diag(S);S3=diag(S);S4=diag(S);%将奇异值矩阵转化为列向量
S1(k1:end)=0;S2(k2:end)=0;S3(k3:end)=0;S4(k4:end)=0;%截取前k个奇异值
if m >=n%对奇异值矩阵进行低秩逼近
S1=[diag(S1);zeros(m-n,n)];S2=[diag(S2);zeros(m-n,n)];
S3=[diag(S3);zeros(m-n,n)];S4=[diag(S4);zeros(m-n,n)];
else
S1=[diag(S1),zeros(m,n-m)];S2=[diag(S2),zeros(m,n-m)];
S3=[diag(S3),zeros(m,n-m)];S4=[diag(S4),zeros(m,n-m)];
end
g1=U*S1*V';g2=U*S2*V';g3=U*S3*V';g4=U*S4*V';%重构得到压缩后的灰度矩阵
g1=uint8(g1);g2=uint8(g2);g3=uint8(g3);g4=uint8(g4);%将矩阵转为可显示的格式
这样就完成了对样例图像的压缩实现,然而仅凭借主观判断是很难对[k]值进行取舍的,若[k]值选取较低,虽然压缩比足够大,然而压缩图像清晰度就可能不足,反之亦然,因此文章将继续介绍一种通过添加数字水印并提取的方法对图像压缩质量进行评估,以完善该算法应用的实用性。
3 基于奇异值分解的数字水印
随着数字产品普及、版权保护以及加密的要求,奇异值分解被应用于向图片中添加数字水印[5-6],例如通过提取水印检查图像是否因为某些攻击受损,标识图片信息等,且通过此方法添加的数字水印不会将图片原本的信息过多改变,具有很好的隐蔽性。
3.1 数字水印添加的基本原理
设[A∈Cm×nr],[A]的奇异值分解形式为:[A=UDVH],添加数字水印矩阵[B],可以进行如下处理:记[Q=B+D],将矩阵[Q]作奇异值分解得:[Q=U1D1VH1],取出奇异值矩阵[D1],重新构建添加完数字水印后的新矩阵[H]:[H=UD1VH][7]。
得到的矩阵[H]就是需要的新矩阵,[H]能保存足够多的图像信息是因为对于图像的数据矩阵而言,不仅矩阵[D]保存了图像信息,左右奇异矩阵[U]和[VH]同样保存了图像信息。
3.2 利用Matlab进行数字水印添加实例
以图像压缩例子中所使用的图像做例子,使用图4作为数字水印图像:
B = imread('D:\examset\watermark.jpg');%读取水印图像信息
B_gray=rgb2gray(B);%灰度化处理
B_gray=double(B_gray);%转换为可计算格式
Q=S+B_gray;
[U1,W,V1]=svd(Q);
H=U*W*V';%将数字水印添加入图2的灰度图像中
这样添加的数字水印可以通过对添加过程取逆的方法重新提取出来,若按照文章介绍的图像压缩方法将添加数字水印后的矩阵进行压缩,则按照下列方法提取出的数字水印矩阵会与原水印矩阵有一些差异,这个差异与压缩比是正相关的:
Q1=U1*W1*V1';Q2=U1*W2*V1';Q3=U1*W3*V1';Q4=U1*W4*V1';
B1=Q1-S;B2=Q2-S;B3=Q3-S;B4=Q4-S;%这些矩阵是根据上节介绍的算法进行压缩的
因此,可以通过计算压缩后提取的B1、B2、B3、B4等矩阵与原水印矩阵B的相似度来评估压缩后图像与原图像的相似程度。
4 图像压缩质量评估数值实验
4.1 评估模型
图像质量评估的方法可以通过许多途径实现[8],文章通过数字水印将构建一个评估模型来评价图像压缩效果,模型由以下几部分组成:
1) 相似度[NC=trB1BHtrBBH],压缩后提取的数字水印矩阵为[B1],原數字水印矩阵为[B]。
2) 压缩比[ρ=mnkm+n+1]。
3) 评估分数[final_score=ρ×NCweight_NC],在本评估模型中取[weight_NC=60]时所得到的数据进行分析。
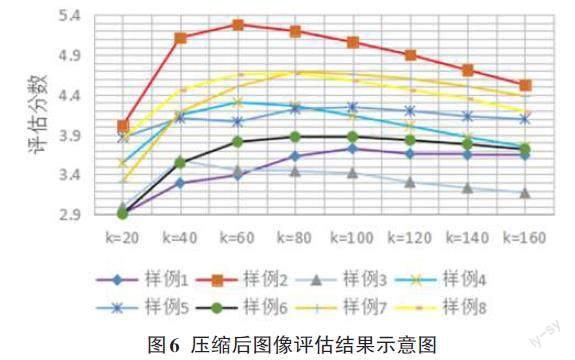
如图6所示,根据本模型构造得到的评分变化曲线具有良好的性质,在最佳压缩比附近区域变化较缓,因此可以通过平均值法得到对绝大多数相同像素大小图像都较优秀的压缩比选取结果。
4.2 评估数值结果
本节汇总了所使用的图像所得的所有数据,采用如下方法进行数据分析:
1) 通过统计相同[k]值时的平均评分及其相似度数据作为分析依据,选取普遍更适用的结果。
2) 由于所采用数据均在同一相似度权重进行采集,因此根据数据分析结果,本节将就其应用需求不同进行分支讨论。
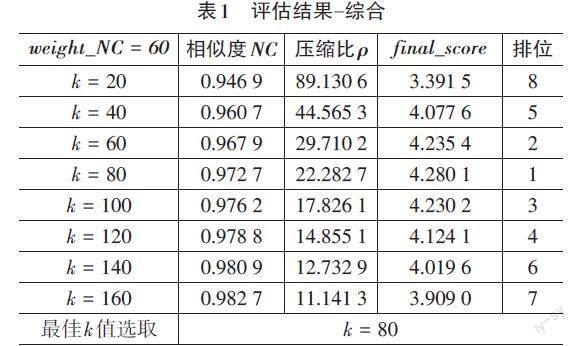
表1为根据总共8组数据得到的综合性结果,数据变化曲线将由折线图展示,根据综合统计,最佳[k]值选取在80可以取得综合最优的效果。
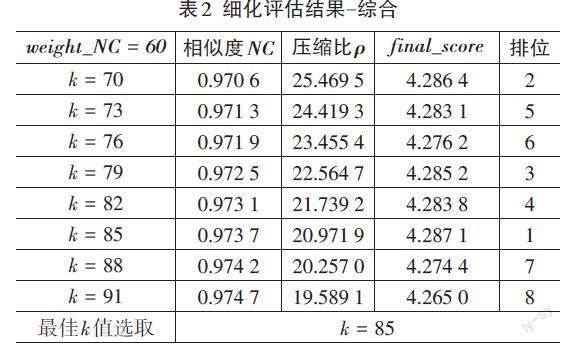
若改变权重,对于相同大小的图像所取到的最佳[k]值也会发生相应改变,文章分析得到的最佳[k]值可参考图3的压缩结果,若采取更高的清晰度权重,则最佳[k]值会相应变大,若需要更高的压缩比,最佳[k]值就相应变小。可以根据实际应用需求进行适当调整,对于固定大小的图像进行处理时,可以通过在最佳[k]值附近进行评估,对于文章所使用的图像数据库,可以进行如下细化,在[k=80]附近进行进一步评估,平均数据如表2所示,可以在此基础上再进行细化,本文不再展示。
最终结果应该取在[k=85]和[k=70]附近,可以根据对于图像清晰度以及压缩空间的具体应用倾向进行选择,而对于不同像素大小的图像,继续扩大分析图像压缩数据的数据库都可以按本方法得到一个能够普遍应用的最佳[k]值,只需要在程序中优先对图像大小进行判断与分类即可,因此本程序具有良好的可拓展性,已经初步具备可实际应用的条件。
5 结论与展望
文章系统性地介绍了适用矩阵奇异值的图像压缩及数字水印算法原理并将其结合,通过Matlab作为工具予以实现,创新性地使用了数字水印提取作为相似度标准,利用评估模型得到了所使用图像同等像素大小适用压缩比并进行细化研究,最终完成了具有初步实用性的图像压缩工具。
该方法还可以进行扩展,通过应用于更多大小的图像数据库来丰富各种处理情况下的最佳压缩比选取,也可以通过进一步缩小压缩比取值间隔来得到更精确的结果,对于相关内容的学习者来说,通过文章获取有关矩阵奇异值分解应用实现的思路应当是有一些帮助的。
参考文献:
[1] 张绍飞,赵迪.矩阵论教程[M].2版.北京:机械工业出版社,2012.
[2] 史荣昌,魏丰.矩阵分析[M].3版.北京:北京理工大学出版社,2010.
[3] 李顺利,姚廷富,余萍,等.矩阵的奇异值分解在图像压缩中应用[J].电脑知識与技术,2022,18(19):1-2,8.
[4] 张帅,董亚芬.基于奇异值分解的数字图像压缩及重构研究[J].信息技术与信息化,2017(S1):112-115.
[5] BARNI M,BARTOLINI F,CAPPELLINI V,et al.A DCT-domain system for robust image watermarking[J].Signal Processing,1998,66(3):357-372.
[6] YEN J C.Watermark embedded in permuted domain[J].Electronics Letters,2001,37(2):80.
[7] 雷超阳,钟一青.奇异值分解算法在数字水印技术中的应用[J].长沙交通学院学报,2008,24(4):78-82.
[8] 王冠军,幸涛,沈静.基于奇异值分解与自然图像统计的无参考图像质量评价方法[J].信息技术与信息化,2022(1):122-125.
【通联编辑:唐一东】
