无等待流水调度量子候鸟协同优化算法

陈林烽 王永录 杨浩 黄重春 汪峰坤 邓春红

摘要：文章提出了一种新颖的量子候鸟协同优化（CQMB） 算法，求解无等待流水调度问题（NWFSP）最小化最大完工时间。算法首先采用量子双链编码方案扩大解空间；全局使用候鸟优化 （MBO）算法进行迭代并与量子旋转门相结合，实现较差个体的改进以及劣势个体与优势个体之间的信息交换，从而提高解的质量；采用变邻域搜索（VNS）策略加速种群收敛并跳出局部最优；测试了基准实例Ta001-Ta090，将CQMB与目前较优算法DWWO比较，DWWO获得较优解的个数为57，而CQMB则为75个。实验结果证明了所提算法具有较强的优化能力，能够有效地求解中小规模无等待流水调度问题。

关键词：无等待流水调度；候鸟优化算法；量子旋转门；最大完工时间；变邻域搜索

中图分类号：TP301.16        文献标识码：A

文章编号：1009-3044（2023）31-0009-05

开放科学（资源服务）标识码（OSID）

0 引言

无等待流水调度问题（No-wait flow-shop scheduling problem， NWFSP） 是一类重要组合优化问题，广泛存在于炼钢、食品加工、化工制造等工业领域[1]。由于在调度过程中，工件加工受到设备、工艺等约束，一旦开始加工就不能中断，直至最后所有加工操作全部完成才得以结束，因此当加工机器m≥3时，NWFSP被证明是一类NP-hard问题[2]。

近年来，许多研究学者将智能优化算法用于求解NWFSP。W. Bozejko等[3]以makespan为目标设计了自我调整混合遗传算法（Hybrid Genetic Algorithm， HGA），实验结果证明HGA算法在求解质量上优于TS（Tabu Search），GASA（Genetic Algorithm and Simulated Annealing Algorithm）算法。D Davendra等[4]针对makespan提出了一种具有自我组织的离散迁徙算法（Discrete Migrating Algorithm，DMA），利用Taillard基准测试实例[5]仿真，实验结果表明DMA的高效性。朱海红等[6]以makespan为指标采用了新颖的量子布谷鸟协同搜索算法（Quantum-inspired Cuckoo Co-search Algorithm， QCCS），并利用基准测试实例Rec仿真，结果证明QCCS算法在求解质量上均优于GA-VNS（Genetic Algorithm and Variable Neighborhood Search），HGA，TS-PSO，TMIIG（Tabu-Mechanism Improved Iterated Greedy）算法。Fuqing Zhao等[7]以makespan为指标采用了新颖的离散水纹优化算法（Discrete Water Wave Optimization，DWWO），通过与TMIIG，IIGA（Improved Iterated Greedy Algorithm），DPSOVND相比可知该算法在中小规模数据集Rec与Ta上取得较优解。

以上算法在求解NWFSP上的成功应用，显示了启发式算法和智能优化算法的优越性。但目前的研究大多基于单一算法，对智能混合优化算法的研究相对较少。量子进化算法（Quantum-inspired Evolutionary Algorithm， QEA）作为新兴智能优化算法，近年来在工程领域掀起了一股热潮[8]。候鸟优化（Migrating Birds Optimization， MBO）算法[9]是一种基于邻域搜索技术的算法，优化思想简单、收敛速度快、较优鲁棒性，在实际应用中已被证明是一种有效的优化方法。

MBO算法目前主要用于求解连续空间优化问题，对于NWFSP这类组合优化问题只有较少的研究。为弥补这一缺陷，本文提出了一种量子候鸟协同优化（Co-optimizate Quantum-inspired Migrating Birds， CQMB）算法尝试求解无等待流水调度中最小化最大完工时间问题。算法采用量子双链编码方案，并使用FL[10]算法产生初始解。引入量子旋转门的概念，即根据当前最优解变化自适应调整旋转角，增加种群多样性，进一步提高解的质量。全局使用MBO算法进行种群迭代，利用量子旋转门，实现劣势个体的自我改进以及劣势个体与优势个体的信息交换，同时引入VNS（Variable Neighborhood Search）[11]算法進一步提高算法的局部搜索能力。本文采用基准测试实例进行实验仿真并与目前较优的智能优化算法作比较，实验结果表明所提算法可以很好地解决组合优化NWFSP，尤其在中小规模下求解最小化最大完工时间问题优化效果显著。

1 问题描述

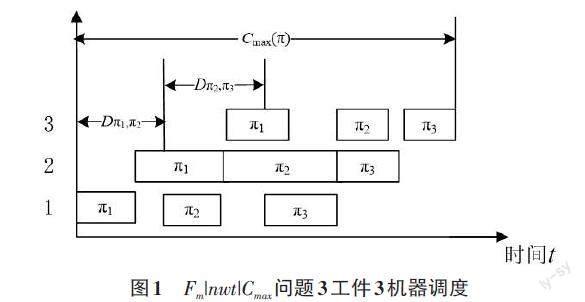
NWFSP可描述为：n个工件在m台机器上加工，每个工件加工顺序和时间给定，要求连续加工，即一旦开始加工便不能被中断；且每个工件只允许被一台机器加工，每台机器只加工一个工件。本文优化目标是求出n个工件的一个加工顺序，使其最大完工时间最小，该问题记为Fm|nwt|Cmax。数学模型如下：

设工件数为{1，2，...，n}和机器数为{1，2，...，m}，Pu，v为工件u在机器v上的加工时间，uÎ{1，2，...，n}，vÎ{1，2，...，m}；Ck，i为机器i上第k个工件的完工时间，kÎ{1，2，...，n}；π为工件按照一定加工次序形成的序列，π={[π1，π2，...，πk]}，[k=2，...，n] 。由于受到工件加工过程无等待的约束，相邻的工件[πk-1]和[πk]之间存在一个开工时间差，记为[Dπk-1，πk]，其计算公式[10]为：

[Dπk-1，πk=max1≤i≤mj=1iPπk-1，j-j=2iPπk，j-1 ，]

[         k= 2，...，n                      ]    （1）

则最大完工时间Cmax（π）为：

[Cmax（π）=k=2nDπk-1，πk+j=1mPπn，j]        （2）

图1为3个工件在3台机器上的Fm|nwt|Cmax调度甘特图。

2 量子候鸟协同优化算法（CQMB）

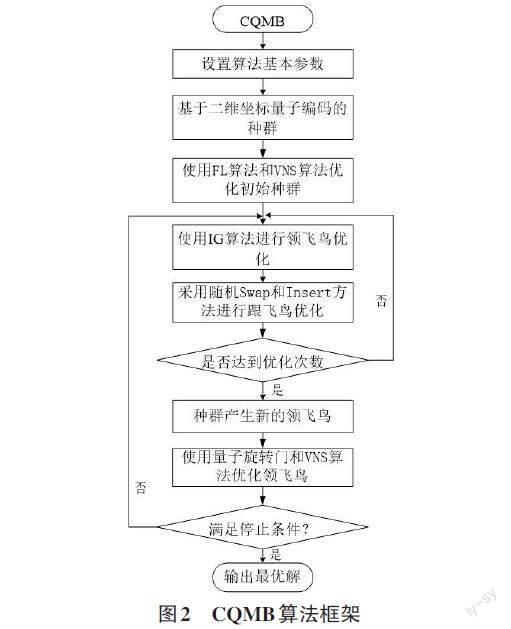
CQMB算法采用候鸟优化算法对种群进行迭代，设计了量子编码、量子旋转门方案，用于优化NWFSP。其基本思想是：首先采用量子双链编码候鸟种群并使用FL算法及VNS 算法产生初始解，在迭代过程中应用候鸟优化算法产生初始候鸟群体，模仿其迁徙过程中V形编队排列，随后进行领飞鸟进化及跟飞鸟进化并采用量子旋转角更新种群，迭代此过程直至满足停止条件。算法基本框架如图2所示。

2.1 量子双链编码和解码

流水调度问题中的解为所有可能形式的作业排列，量子个体中的每个量子位可代表一个作业，且[φ]的概率符用量子角形式表示，即：

[φ=[α，β]T=[cos（θ），sin（θ）]T]           （3）

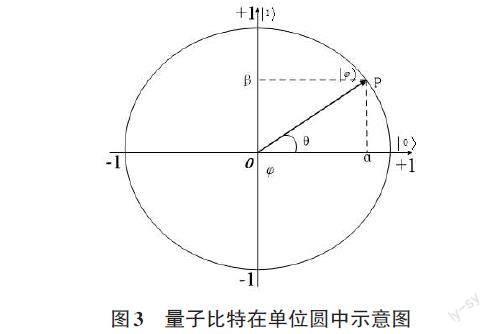
因此，量子比特可以由圆上的一点[P（cos（θ），sin（θ））] 描述，如图3所示。长度为n的量子个体q由n个量子位组成，应用至此环境中q即为种群个体，可描述为：

[q=cos（θ1）sin（θ1）cos（θ2）sin（θ2）……cosθnsinθn]      （4）

群体初始化时，量子角[θj] （1≤j≤n）在[0，2π]内随机生成。量子个体的解码过程如下：令q的第j个量子位的概率幅[αj]表示为当前调度序列第j个作业在区间[0，1]的映射值，相应产生[α1，α2，...，αn]解向量，采用LOV（largest-order-value）規则[10]生成一组调度作业[π1，π2，...，πn]。

2.2 算法描述

为了解决Fm|nwt|Cmax问题，采用量子双链编码方案，候鸟优化算法，变邻域搜索算法和量子旋转门策略。具体描述如下：

步骤1：初始化各参数，包括种群大小[ps]，最大迭代次数[imax]，邻域大小[Cnum]，分享邻域大小[Snum]，巡回次数K，数组Lp[[]]、Rp[[]]、[Sn_L[]]和[Sn_R[]]等。

步骤2：初始化种群，随机生成[ps]个个体[{x1，x2，...，xps}]。

步骤3：执行量子编码种群[{x1，x2，...，xps}←Encoding（）]，生成ps个调度序列π，调用Min函数生成初始解π'。

步骤4：对[初始解π']执行变异的FL算法及VNS算法进行优化。

步骤5：令[i=1，2，...，imax]，开始进入循环操作。

步骤6：[令j=1，2，...，K]，开始进入循环操作。

步骤7：令经过步骤4优化后的初始解[π'']为领飞鸟的解，并用IG算法生成领飞鸟的[Cnum]个邻域解[LBc]，其中，[LBc[]=N1，N2，...NCnum，Nbest=Min{N1，N2，...，NCnum}]。

步骤8：将[Nbest]与[领飞鸟的解π']比较目标值[Cmax，]若小则替换。

步骤9：将[LBc[]]中未被使用的[Cmax]最佳的[2Snum]个邻域解随机填入[Sn_L[]]和[Sn_R[]]，使得两个数组都包含[Snum]个解。

步骤10：对于[m=1，2，...，（ps-1）/2]，进行左边跟飞鸟的优化。

步骤11：随机使用[Swap（）]和[Insert（）]的方法生成[Lp[m]]的[Cnum-Snum]个邻域解，然后和[Sn_L[]]合并构成[Lp[m]]的邻域解集合[FBc[m]]。[令Nbest=Min（Cmax（FBc[]））]，若[Cmax]（[Nbest]） < [CmaxLpm，] 则将[Nbest赋值给Lp[m]]，并将[FBc[]]中未被使用的[Cmax]最佳的[Snum]个邻域解填入[Sn_L[]]。

步骤12：对于m = [1，2，...，（ps-1）/2]，进行右边跟飞鸟的优化。

步骤13：随机使用[Swap（）]和[Insert（）]的方法生成[Rp[m]]的[Cnum-Snum]个邻域解，然后和[Sn_R[]]合并构成[Rp[m]]的邻域解集合[FBc[m]]。[令Nbest=Min（Cmax（FBc[]））]，若[Cmax]（[Nbest]） < [CmaxRpm] 则将[Nbest赋值给Rp[m]]，并将[FBc[]]中未被使用的[Cmax]最佳的[Snum]个邻域解填入[Sn_R[]]。

步骤14：循环至K次进行步骤15操作，否则返回步骤6。

步骤15：将左右两翼的第一个解[Lp[1]]和[Rp[1]]相比较，其目标值将较小者作为领飞鸟，旧的领飞鸟自动回至所在翼的尾部。

步骤16：对当前解执行[VNS]优化，增强局部搜索能力，并通过根据当前最优解变化自适应调整旋转角[Δθ]，若更优则替换领飞鸟的解。

步骤17：输出最优解及对应的工件加工序列。

步骤18：循环至[imax]时算法结束，否则返回步骤[5]进行迭代。

CQMB算法的时间开销主要集中在步骤4、5、16优化阶段，步骤4、16的时间复杂度为O（mn4），步骤5的时间复杂度为O（[imax]），若每次运行k次，则CQMB时间复杂度为O（km[imaxn]4）。

3 仿真实验与算法性能评价

3.1 参数设置

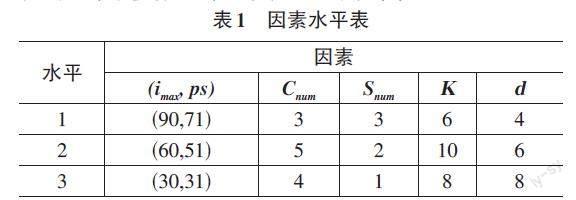
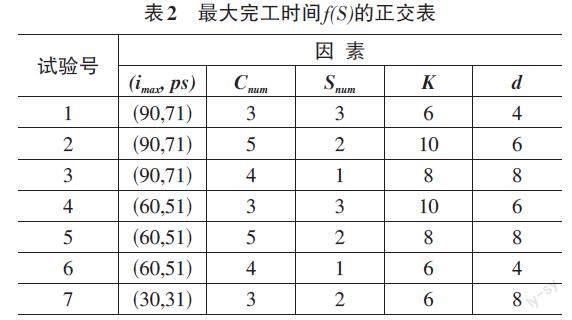
本文所提出算法是针对Fm|nwt|Cmax问题，采用基准测试实例Rec、Car与Ta进行性能评估。按问题规模Car数据集11×5到8×8的8组，每组1个实例；Rec数据集20×5到75×20的7组，每组3个实例；Ta数据集20×5到100×20的9组，每组10个实例；每个实例重复计算30次。算法采用Visual Studio实现，在CPU 2.83GHz、RAM 4GB的PC机上运行。设置工件数n，m为机器数。其他参数各数值采用正交实验设计方法，表1是每个参数因素及其对应的水平值。

其中imax表示最大迭代次数，ps是种群大小，Cnum、Snum、K和d分别表示邻域大小、分享邻域大小、巡回次数和IG算法中序列的删减个数。

从表1的5因素3水平表可知，正交表可安排18组试验，即L18（37），将最后两列设置为空置列，如表2所示。以50×10中一个实例为实验数据，采用Taguchi实验[12]方法，计算每组实验的信噪比（S/N ratio）。实验结果分析时， S/N ratio值的计算能够很好地保护目标函数值。在大多数情况下，每个水平对应的目标函数值互相都非常接近，因此S/N ratio的影响非常重要。S/N ratio 计算公式如下：

[SN ratio=-10log10f（S）2]           （7）

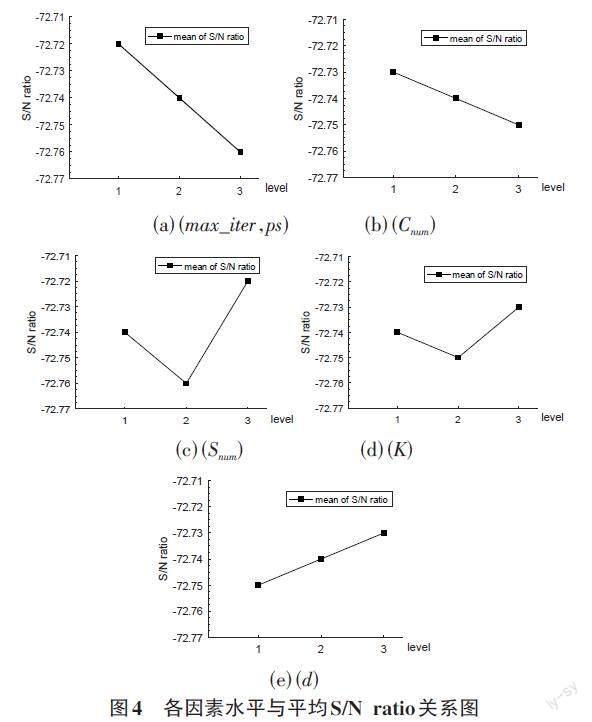
其中，f（S）是目标函数值，即最大完工时间，图4为各因素水平与平均S/N ratio关系图。

在CQMB算法中，S/N ratio取较大值较好。由图4可得，（imax， ps）、Cnum、Snum、K 和d分别在水平1、1、3、3、3值较大，因此可得出参数imax =90、ps=71、Cnum=3、Snum=1、K=8、d=8。

3.2 性能比较

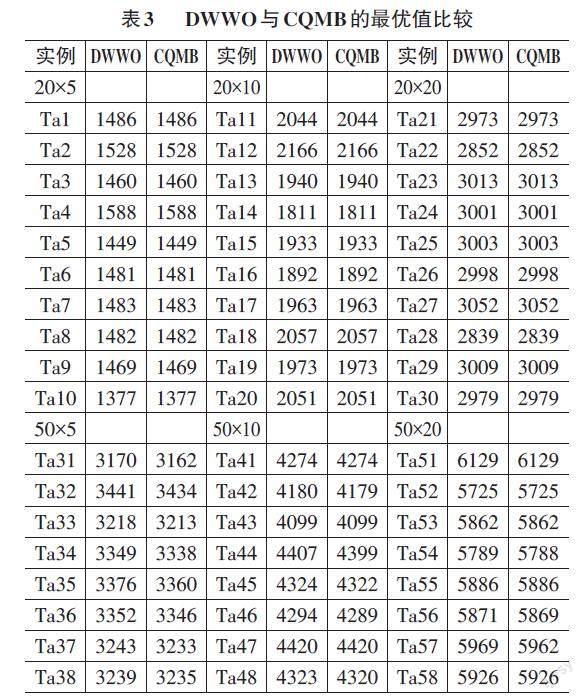
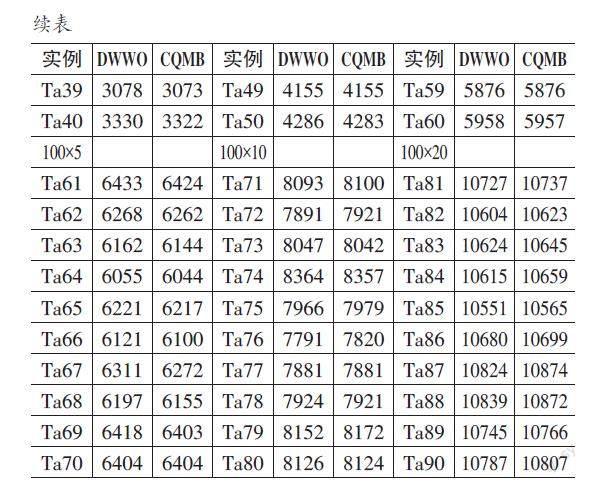
Ta数据集上的性能测试。为了更加全面地体现算法寻优能力，采用基准测试实例Ta数据集测试，并与当前较优算法DWWO比较，比较结果如表3所示。由表3可以看出，在n=20、m=5、10和20时，本文算法与DWWO算法全部达到最优。在n=50、100，m=5时，除Ta70与DWWO优化结果相同外，所提算法均优于DWWO算法；在n=50、100，m=10时，CQMB达到较优解的个数为15，而DWWO仅有10个。在n=50、m=20时，CQMB得到10个较优解，而DWWO仅有6个。在n=100、m=20时，所提算法優化效果不是特别明显。从算法总体求解质量看，在中小规模问题中本文所提算法优于所比较的算法。

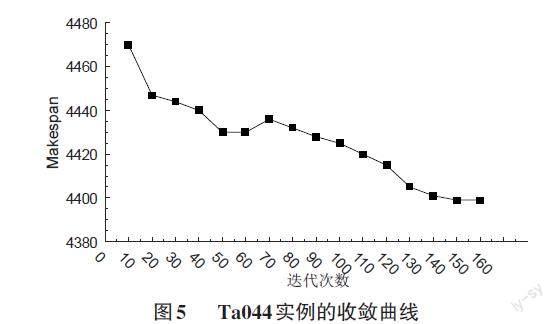
以Ta044为例，本文算法求解得到的最小完工时间为4 399，而DWWO算法却为4 407。得到最优解的序列为：{20，10，19，9，44，29，46，34，13，28，5，8，22，17，14，25，12，26，45，41，38，36，35，30，21，1，37，2，11，6，49，15，47，43，24，50，32，4，23，18，40，16，39，31，48，3，27，7，33，42}，括号中的数字代表工件的序号，该序列代表了工件的加工顺序。

为了体现算法的收敛性，图5给出了算法求解Ta044实例的收敛曲线，由图5可以看出，算法在最初具有很快的收敛速度，但随着迭代次数的增加，算法的收敛性变缓，甚至出现局部收敛，但算法具有跳出局部最优的能力最终得到较好的解。

4 结论

本文针对Fm|nwt|Cmax问题提出了一种新颖高效的CQMB算法。该算法模拟候鸟迁徙与跟飞鸟替换领飞鸟过程，智能达到一种高效的寻优模式；算法采用量子双链编码方案扩大解空间，并引入量子旋转门对当前最优解变化自适应调整旋转角，增加种群多样性，进一步提高解的质量并使用变邻域算法（VNS） 加速种群收敛并跳出局部最优。通过选取不同规模Benchmark问题算例测试，并与目前较优的几种算法相比较。结果表明，所提算法在求解中小规模Fm|nwt|Cmax问题均优于其他算法。

参考文献：

[1] 张梓琪，钱斌，胡蓉.混合交叉熵算法求解复杂零等待流水线调度问题[J].控制理论与应用， 2021， 38（12）：16.

[2] 郑堃，练志伟，王玉国，等.改进激素算法求解置换流水车间调度问题[J].电子科技大学学报，2022，51（6）：890-903.

[3] BOŻEJKO W，Makuchowski M.Solving the no-wait job-shop problem by using genetic algorithm with automatic adjustment[J].The International Journal of Advanced Manufacturing Technology，2011，57（5/6/7/8）：735-752.

[4] DAVENDRA D，ZELINKA I，BIALIC-DAVENDRA M，et al.Discrete self-organising migrating algorithm for flow-shop scheduling with no-wait makespan[J].Mathematical and Computer Modelling，2013，57（1/2）：100-110.

[5] TAILLARD E.Benchmarks for basic scheduling problems[J].European Journal of Operational Research，1993，64（2）：278-285.

[6] ZHU H H，QI X M，CHEN F L，et al.Quantum-inspired cuckoo co-search algorithm for no-wait flow shop scheduling[J].Applied Intelligence，2019，49（2）：791-803.

[7] ZHAO F Q，LIU H A，ZHANG Y，et al.A discrete Water Wave Optimization algorithm for no-wait flow shop scheduling problem[J].Expert Systems With Applications，2018（91）：347-363.

[8] 錢洁，郑建国，张超群，等.量子进化算法研究现状综述[J].控制与决策，2011，26（3）：321-326，331.

[9] DUMAN E，UYSAL M，ALKAYA A F.Migrating Birds Optimization：a new metaheuristic approach and its performance on quadratic assignment problem[J].Information Sciences，2012（217）：65-77.

[10] FRAMINAN J M，LEISTEN R.An efficient constructive heuristic for flowtime minimisation in permutation flow shops[J].Omega，2003，31（4）：311-317.

[11] MLADENOVIĆ N，TODOSIJEVIĆ R，UROŠEVIĆ D，et al.Solving the Capacitated Dispersion Problem with variable neighborhood search approaches：from basic to skewed VNS[J].Computers & Operations Research，2022（139）：105622.

[12] DAO T P，HUANG S C，THANG P T.Hybrid Taguchi-cuckoo search algorithm for optimization of a compliant focus positioning platform[J].Applied Soft Computing，2017（57）：526-538.

【通联编辑：唐一东】